2. ИСПОЛЬЗОВАНИЕ ЗАКОНОВ ОМА И КИРХГОФА ПРИ РАСЧЕТЕ И АНАЛИЗЕ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
Согласно закону Ома в замкнутой неразветвленной электрической цепи (рис. 2):

Рис. 2. Незамкнутая электрическая сеть
А в любом пассивном элементе цепи, например с сопротивлением r2,

Выражение (1) справедливо при совпадающих направлениях ЭДС Е и тока I, а выражение (2) – при совпадающих направлениях напряжения U и тока I, что и следует учитывать при нанесении на схеме стрелок, указывающих положительные направления в случае использования закона Ома.
Согласно первому закону Кирхгофа алгебраическая сумма токов ветвей, соединенных в любой узловой точке электрической цепи, равна нулю, т. е.

Со знаком «+» в уравнение следует включать токи, положительные направления которых обращены к узлу, со знаком «–» – токи, положительные направления которых обращены от узла (можно и наоборот).
Согласно второму закону Кирхгофа в любом замкнутом контуре электрической цепи алгебраическая сумма ЭДС равна алгебраической сумме напряжений на всех резистивных элементах контура, т. е.

Часто в электрических цепях встречаются элементы, между выводами которых имеются те или иные напряжения U (например, напряжение сети, напряжение, снимаемое с делителя напряжения, и т. д.).
Учитывая это, вместо (4) удобнее использовать следующую форму записи второго закона Кирхгофа:
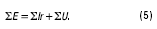
При этом ЭДС, напряжения и токи, положительные направления которых совпадают с направлением обхода контура при составлении уравнения (5), следует включать в уравнение со знаком «+», а те, положительные направления которых не совпадают с направлением обхода контура, со знаком «–» (можно и наоборот).
При составлении уравнений по второму закону Кирхгофа следует включать в них либо ЭДС и падение напряжения во внутренних сопротивлениях активных элементов, либо только их напряжения.