Все науки. №6, 2023. Международный научный журнал - читать онлайн

УДК 150.145

Насриддинов Отадавлат Усубжонович

Старший преподаватель кафедры «Естественный наук» факультета компьютерного инжиниринга Ферганского филиала Ташкентского Университета Информационных Технологий

Ферганский филиал Ташкентского Университета Информационных Технологий, Фергана, Узбекистан

Аннотация. Невозможность интуитивного понимания самого различного спектра квантовых явлений сводит к необходимости использования перед всеми эмпирическими и экспериментальными действиями всех физико-математических методов. Одним из самым популярным и важных в данном ключе является линейное дифференциальное уравнение в частных производных, описывающее изменение в пространстве и во времени чистого состояния, задаваемое волновой функцией, в гамильтоновых квантовых системах для фотонных явлений выражаемое в стационарном состоянии.

Ключевые слова: уравнение Шрёдингера, стационарное состояние, спектральные задачи, квантование, дифференциальное уравнение, физико-математическое вычисление и моделирование.

Annotation. The impossibility of intuitive understanding of the most diverse spectrum of quantum phenomena reduces to the need to use all physical and mathematical methods before all empirical and experimental actions. One of the most popular and important in this vein is a linear partial differential equation describing the change in space and time of the pure state, given by the wave function, in Hamiltonian quantum systems for photonic phenomena expressed in a stationary state.

Keywords: Schrodinger equation, stationary state, spectral problems, quantization, differential equation, physical and mathematical calculation and modeling.

Перед представлением самого вопроса, стоит отметить представление самого одномерного стационарного уравнения Шредингера, являющееся линейным обыкновенным дифференциальным уравнением второго порядка (1), которое применяется в том числе и для решения задач спектрального плана при волновом моделировании фотонных явлений.

С целью решения такого подхода задач необходимо ввести граничные условия (2), в зависимости от постановки коих можно определить общее описание ситуации и при этом стоит обратить внимание на констатирование показателей (3).

Разумеется, можно было бы постараться определить общее решение, однако, к большому сожалению, это попросту невозможно и необходимо вводить те или иные граничные условия, которые сводятся из тех или иных условий. Яркий пример таких состояний – решение для свободной частицы, которая является по своей сути плоской волной. И если принять потенциальное уравнение для свободной частицы, в том числе и при принятии корпускулярной формы фотонов, можно получить уравнение (4).

Одним из частных решений является функция (5), выводимая через прямое решение дифференциального уравнения второго порядка.

В (4) константа Е может принимать практически все значения выше нуля, именно отсюда можно сделать вывод, что значения относятся к непрерывному спектру. Более того, для определения его границ необходимо использовать интегральное уравнение (6), откуда и получается получаемая константа С из (5).

Отсюда и получается значение (7).

И наконец, при подстановке, можно получить решение уравнения (4), для случая свободной частицы, которая в том числе, при волновом исчислении является суперпозицией плоских волн (9).

Но если это был только один из частных случаев, то стоит рассмотреть и случай нахождения в одномерной потенциальной яме с бесконечно высокими стенками. Ведь если обратить внимание на представления этого вопроса, то это вполне может быть сводимый к этому случай в лице входа фотона в тот или иной атом, при условии приближения к электронным оболочкам, выход из коих и может сыграть роль бесконечно высоких стенок потенциальной ямы. Также ещё один более масштабный макро-пример – это приближение к чёрной дыре фотонного излучения. Для таких случаев и интервалов уравнение Шредингера совпадает с представлением согласно (4), откуда граничные условия для волновой функции, ранее обозначаемые алгебраически (2), представляются как (10—11).

Решение, как можно было обратить внимание из прочих частных решений может быть сведено к форме (12).

Но если теперь для этого вида ввести граничные формы, можно прийти к решению показателя энергии как (13).

Наконец, теперь остаётся лишь ввести собственные функции, наряду с общей нормировкой и получить результирующее решение (14).

Таким образом были рассмотрены некоторые из частных решений линейного уравнения Шредингера, каждая из коих может быть интерпретирована в лице решения того или иного вида или формы, количество коих может быть огромным.

Использованная литература

1. Allday Jonathan. Quantum Reality: Theory and Philosophy. 2^nd edition. – CRC Press, 2023. – 505 p. – ISBN: 978-1-032-12734-7.

2. Aaserud Finn, Kragh Helge (eds.) One Hundred Years of the Bohr Atom. Proceedings From a Conference. – Copenhagen: Scientia Danica, Det Kongelige Danske Videskabernes Selskab, 2015. – 559 p.

3. Agarwala A. Excursions in III-Condensed Quantum Matter: From Amorphous Topological Insulators to Fractional Spins. Springer, 2019. – 177 p. – (Springer Theses). – ISBN: 9978-3-030-21510-1.

4. Audelsburger M. Artifical Gauge Fields with Ultracold Atoms in Optical Lattices (Springer Theses). Springer International Publishing, Switzerland, 2016. – 180 p. – ISBN: 3319258273

5. Aktosun T., Weder R. Direct and Inverse Scattering for the Matrix Schrodinger Equation. Springer, 2021. – 631 p. – (Applied Mathematical Sciences). – ISBN: 978-3-030-38430-2.

6. Akulin V. M. dynamics of Complex Quantum Systems 2^nd ed. – Springer, 2014. – 677 pp.

7. Alber G. et al. Quantum Information: An Introduction to Basic Theoretical Concepts and Experiments. Alber G., Beth Th., Horodecki M., Horodecki P., Horodecki R., Potteler M., Weinfurter H., Werner R., Zeilinger A. – Springer, 2001. – 195 p. – (Springer Tracts in Modern Physics 173). – ISBN 3-540-41666-8.

8. Albeverio S., Kondratiev Yu., Kozitsky Yu., Rockner M. The Statistical Mechanics of Quantum Lattice Systems: A Path Integral Approach. European Mathematical Society, 2009. – 393 p. – (EMS Tracts in Mathematics 08). – ISBN 978-3-03719-070-8.

9. Alicki R., Lendi K. Quantum Dynamical Semigroups and Applications. Springer, 2007. – 129 p. – (Lecture Notes in Physics 717).

10. Гольдин, Л. Л. Квантовая физика. Вводный курс / Л. Л. Гольдин, Г. И. Новикова. – М.: [не указано], 2002. – 823 c.

11. Иродов, И. Е. Задачи по квантовой физике / И. Е. Иродов. – М.: [не указано], 1991. – 228 c.

12. Иродов, И. Е. Квантовая физика. Основные законы / И. Е. Иродов. – М.: [не указано], 2002. – 768 c.

13. Иродов, И. Е. Квантовая физика. Основные законы / И. Е. Иродов. – М.: Бином. Лаборатория знаний, 2014. – 662 c.

14. Мигдал, А. Б. Квантовая физика и Нильс Бор / А. Б. Мигдал. – М.: [не указано], 1987. – 153 c.

УДК 537.812

Алиев Ибратжон Хатамович

Генеральный директор OOO «Electron Laboratory»; Президент Научной школы «Электрон»; Студент 3 курса факультета математики-информатики Ферганского государственного университета OOO «Electron Laboratory», Научная школа «Электрон», Маргилан, Узбекистан

Ферганский государственный университета, Фергана, Узбекистан

Аннотация. Развитие современной науки и техники влечёт за собой появление огромного количества новых достижений и результатов в самых различных областях человеческого познания, благодаря чему сегодня стало известно о появление довольно экзотического и удивительного источника электрической энергии в лице резонансных ядерных реакций. Сама суть нейтронных ядерных реакций была впервые представлена в ряд научных статей, монографиях, учебном пособии автора этого направления в науке – Алиева И. Х., представляющая отдельный метод доведения каждой из выбранных определённых экзо-энергетических ядерных реакций до состояния резонанса, то есть момента, когда эффективность процесса становится максимальной.

Ключевые слова: электромагнетизм, физика резонансных ядерных реакций, ядерная физика, математическое моделирования, полноценное исследование, аналитический анализ.

Annotation. The development of modern science and technology entails the emergence of a huge number of new achievements and results in various fields of human cognition, thanks to which today it has become known about the appearance of a rather exotic and amazing source of electrical energy in the face of resonant nuclear reactions. The very essence of neutron nuclear reactions was first presented in a number of scientific articles, monographs, and a textbook by the author of this direction in science – Aliyev I. H., representing a separate method of bringing each of the selected specific exo-energetic nuclear reactions to a state of resonance, that is, the moment when the efficiency of the process becomes maximum.

Keywords: electromagnetism, physics of resonant nuclear reactions, nuclear physics, mathematical modeling, full-fledged research, analytical analysis.

Введение

Ведь если обратить внимание, при проходе определённой ядерной реакции необходимо проведение её анализа и именно новый метод общего анализа ядерной реакции, введённый Алиевым И. Х. и стал основой для демонстрации подобного типа явлений, в коих изначально описывается сама реакций, затем её параметры с том числе, выход (1), порог (2), кинетические входящие и выходящие энергии (3—4). Далее стоит обратиться к тому, что благодаря правильному подбору близкому к кулоновскому барьеру (5) энергии у входящей лёгкой заряженной частицы, ядерной эффективное сечение (6), зависимое от волны де Бройля (7), резко увеличивается, что в последующем приводит к увеличению общего тока пучка (8), вошедшего во взаимодействие.

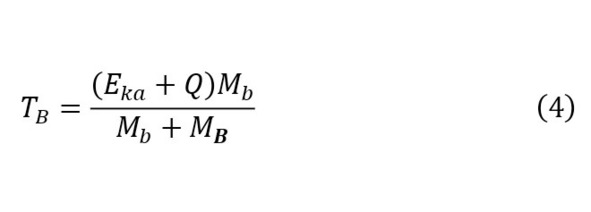
Таким образом, можно отметить, что подобная система позволяет производить одиночные или одиночные-многоступенчатые реакции. Однако, в более модифицированной вариации установки для таких реакций, отчасти описанная в последующей монографии и учебном пособии, посвящённая физике ускорителей заряженных частиц, отмечалось о возможности проведения сразу нескольких, а именно исследованных на тот момент 6 основных резонансных ядерных реакциях при помощи использования электромагнита.

В данном случае, направление пучка в каждый из отделений реакции создаёт импульсный переход и приводит к необходимости создания многоступенчатого переменного и одновременно строго дискретного магнитного поля со стороны электромагнита, что уже на этой стадии является довольно интересной задачей. Но что ещё больше заслуживает внимания, так это факт в дальнейшем резкого увеличения токов приходящего пучка.

Центральная часть

И для контроля увеличенного пучка, необходимо изучить природу электромагнитного поля. Электрическое поле подвластно своему измерению благодаря такому понятию как напряжённость (10), что характеризуется воздействием на поля определённого заряда на некотором расстоянии на зондовый заряд благодаря силе Кулона (9).

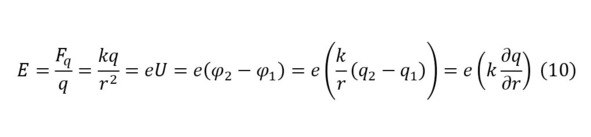
Такой же возможностью к вычислению обладает и магнитное поле, для него эта величина называется магнитной индукцией, измеряемая в единицах – Тесла, названные в честь великого и гениальнейшего сербского учёного своего времени Николы Тесла. Поскольку была ранее объяснена причина возникновения магнитного поля, то и её первое определение вычисляется через уравнения Максвелла и их следствия (11—14), подробнее о коих рассмотрено неоднократно.

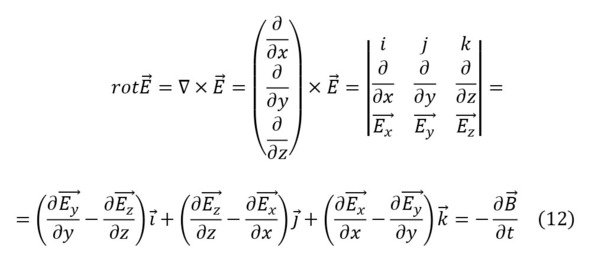
Кроме того, если сделать определённые исключения и благодаря свойству действия магнитного поля, в частности, и в статике, то закономерности для них будут подобны законам Кулона (15—16), а также в некоем поле будут следствием условия геометрии поля, что изначально предполагает теорема господина Андре Мари Ампера о циркуляции магнитного поля (17).

Однако, все эти параметры были приведены только для общего вида, но если обращаться к конкретным примерам, то в первую очередь стоит привести определение вектора магнитной индукции прямого провода с известным током и известном расстоянии от него определяется благодаря (19).

При этом важно отметить, что для определения вектора магнитной индукции необходимо определить магнитную проницаемость среды – это и есть параметр, демонстрирующий возможность того или иного материала проводить магнитное поле. Практически тоже самое можно сказать и о таком объекте как соленоид – самом настоящем электромагните, состоящий из спиралевидной проволоки и сердечника. И это небольшое поверхностное описание элементов электромагнетизма приводит к описанию их действия на заряды.

Где таким образом, если свободный заряд попадает в магнитное поле, то он попадает под воздействие силы магнитной индукции под действием определённой силы Лоренца (20), под действием которого с учётом создаваемой центробежной силы (21), заряд начинает своё вращение с радиусом (22).

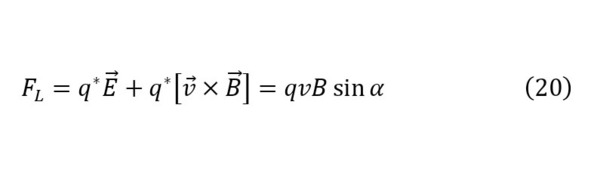
Более того, существует и релятивистская форма записи этой же формулы (23—24).

Но эти заряды при вращении опять же создают переменное электрическое поле, которое создаёт переменное магнитное поле – паразитирующее, а оно в свою очередь новое электрическое. То есть и в этом случае, ситуация с электромагнитном повторяется, что требует более подробного рассмотрения.

Когда один заряд попадает в магнитное поле действует магнитное поле, но, когда большинство зарядов в проводнике начинают попадать в такое определённое поле, действует уже сила Ампера (25—27), которая символизирует вектор силы, образуемое уже всем проводников в магнитном поле.

В результате чего можно получить подобную картину общего описания явлений.

Заключение

В результате этого общего анализа можно сказать, что применение и развитие электромагнетизма может привести к совершенствованию самых различных областей науки, даже самых новых как в теоретическом, так и практическом плане. И более того, каждая из этих нововведений совершенствует все эти идеи всё больше и больше!

Использованная литература

1. Браун, А. Г. Атомная и ядерная физика. Элементы квантовой механики. Практикум: Учебное пособие / А. Г. Браун, И. Г. Левитина. – М.: Инфра-М, 2019. – 352 c.

2. Дельцов, В. П. Физика: дойти до самой сути! Настольная книга для углубленного изучения физики в средней школе: Атомная и ядерная физика / В. П. Дельцов, В. В. Дельцов. – М.: Ленанд, 2017. – 176 c.

3. Калашников, Н. П. Практикум по решению задач по общему курсу физики. Основы квантовой физики. Строение вещества. Атомная и ядерная физика: Учебное пособие / Н. П. Калашников. – СПб.: Лань, 2014. – 240 c.

4. Ланге, В. Н. Физические парадоксы, софизмы и занимательные задачи. Книга 2: Электричество и магнетизм. Колебания и волны. Оптика. Теория относительности. Атомная и ядерная физика / В. Н. Ланге. – М.: КД Либроком, 2018. – 232 c.

5. Ландсберг, Г. С. Элементарный учебник физики Колебания и волны, оптика, атом. и ядерная физика т.3 / Г. С. Ландсберг. – М.: Физматлит, 2012. – 664 c.

6. Ландсберг, Г. С. Элементарный учебник физики т.3 Колебания и волны, оптика, атомная и ядерная физика. 15-е и / Г. С. Ландсберг. – М.: Физматлит, 2016. – 664 c.

7. Ландсберг, Г. С. Элементарный учебник физики. Т.3. Колебания волны. Оптика. Атомная и ядерная физика: Учебное пособие / Г. С. Ландсберг. – М.: Физматлит, 2016. – 664 c.

8. Мухин, К. Н. Экспериментальная ядерная физика. Т. 1. Физика атомного ядра: Учебник / К. Н. Мухин. – СПб.: Лань, 2009. – 384 c.

9. Мухин, К. Н. Экспериментальная ядерная физика. Т. 1. Физика атомного ядра: Учебник / К. Н. Мухин. – СПб.: Лань, 2008. – 384 c.

10. Мухин, К. Н. Экспериментальная ядерная физика. Т. 2. Физика ядерных реакций: Учебник / К. Н. Мухин. – СПб.: Лань, 2009. – 326 c.

11. Мухин, К. Н. Экспериментальная ядерная физика. Т. 2. Физика ядерных реакций: Учебник / К. Н. Мухин. – СПб.: Лань, 2008. – 336 c.

12. Ракобольская, И. В. Ядерная физика / И. В. Ракобольская. – М.: Красанд, 2014. – 248 c.

13. Сивухин, Д. В. Общий курс физики Т.5. Атомная и ядерная физика: Учебное пособие / Д. В. Сивухин. – М.: Физматлит, 2008. – 784 c.

14. Сивухин, Д. В. Общий курс физики Т.5 Атомная и ядерная физика: Учебное пособиев 5 т. / Д. В. Сивухин. – М.: Физматлит, 2008. – 784 c.

15. Сивухин, Д. В. Общий курс физики Том 5 Атомная и ядерная физика: Учебное пособие / Д. В. Сивухин. – М.: Физматлит, 2008. – 784 c.

16. Сивухин, Д. В. Общий курс физики. В 5 т. Т. 5. Атомная и ядерная физика, стер / Д. В. Сивухин. – М.: Физматлит, 2008. – 784 c.

17. Астапенко, В. А. Взаимодействие электромагнитных импульсов с классическими и квантовыми системами. Учебное пособие / В. А. Астапенко. – М.: МФТИ, 2013. – 232 c.

18. Бамбуров, В. Г. Монооксид европия для спинтроники: Монография / В. Г. Бамбуров, А. С. Борухович. – М.: Лань, 2015. – 779 c.

19. Бардзокас, Д. И. Распространение волн в электромагнитоупругих средах / Д. И. Бардзокас. – Москва: Высшая школа, 2003. – 333 c.

20. Бармасов, А. В. Курс общей физики для природопользователей. Колебания и волны / А. В. Бармасов, В. Е. Холмогоров. – М.: БХВ-Петербург, 2012. – 256 c.

21. Боков, В. А. Физика магнетиков. Учебное пособие / В. А. Боков. – М.: Невский Диалект, БХВ-Петербург, 2002. – 272 c.

22. Васильков, А. В. Источники электропитания / А. В. Васильков, И. А. Васильков. – М.: Форум, 2012. – 400 c.

23. Воронов, В. К. Современная физика. Конденсированное состояние / В. К. Воронов, А. В. Подоплелов. – М.: ЛКИ, 2008. – 336 c.

24. Гантмахер, В. Ф. Электроны в неупорядоченных средах / В. Ф. Гантмахер. – М.: ФИЗМАТЛИТ, 2003. – 176 c.

25. Дудь, Александр Петрович Лекция 3 Электромагнитная Картина Мира / Дудь Александр Петрович. – Москва: СИНТЕГ, 2012. – 786 c.

26. Зильберман, Г. Е. Электричество и магнетизм / Г. Е. Зильберман. – М.: Интеллект, 2008. – 337 c.

27. Зисман, Г. А. Курс общей физики. В 3 томах. Том 2. Электричество и магнетизм / Г. А. Зисман, О. М. Тодес. – М.: Лань, 2007. – 352 c.

28. Иванов, А. Е. Электродинамика. Учебник / А. Е. Иванов. – М.: КноРус, 2016. – 560 c.

29. Иродов, И. Е. Электромагнетизм. Основные законы / И. Е. Иродов. – М.: Бином. Лаборатория знаний, 2014. – 320 c.

30. Котырло, Т. В. Электричество и магнетизм. Практический курс физики / Т. В. Котырло, Г. Г. Спирин, В. В. Евстигнеев. – М.: Высшая школа, 2008. – 448 c.

31. Крамм, М. Н. Сборник задач по основам электродинамики / М. Н. Крамм. – Москва: ИЛ, 2011. – 256 c.

32. Лунин, В. П. Электротехника и электроника. Электромагнитные устройства и электрические машины. Учебник и практикум для академического бакалавриата / В. П. Лунин. – М.: Юрайт, 2004. – 605 c.

33. Парселл, Э. Электричество и магнетизм. Берклеевский курс физики / Э. Парселл. – М.: Лань, 2005. – 420 c.

34. Паршаков, А. Н. Физика линейных и нелинейных волновых процессов в избранных задачах. Электромагнитные и акустические волны. Учебное пособие / А. Н. Паршаков. – М.: Интеллект, 2014. – 144 c.