Расчеты геометрии.
Отрезок на плоскости.
Исходные данные:
Даны координаты концов отрезка:
Абсцисса x1 = 10; Ордината y1 = 20;
Абсцисса x2 = 50; Ордината y2 = 80;

Расчет:
Длина отрезка:
L= sqrt((x1-x2)*(x1-x2))+((y1-y2)*(y1-y2));
L= sqrt((10-50)*(10-50))+((20-80)*(20-80));
L= sqrt( 5200 ); L= 72,11102551…
Угол между осью Х-Х и отрезком:
U= arctan((y2-y1)/(x2-x1));
U= arctan( 60 / 40 ); U= 56,30993247…
Отрезок в пространстве.
Исходные данные:
Абсцисса x1 = 10; Ордината y1= 20;
Высота z1 = 30;
Абсцисса x2 = 40; Ордината y2= 60;
Высота z2 = 80;
Примечание: Ось Z направлена в зенит.

Расчет:
Длина отрезка в пространстве:
L = sqrt((x1-x2)*(x1-x2))+((y1-y2)*(y1-y2))+((z1-z2)*(z1-z2));
Длина отрезка L = 70,71068;
Длина проекции отрезка на плоскость Y-Z:
Lyz = sqrt((y1-y2)*(y1-y2))+((z1-z2)*(z1-z2));
Длина отрезка Lyz = 64,0312424;
L = sqrt((x1-x2)*(x1-x2))+((y1-y2)*(y1-y2))+((z1-z2)*(z1-z2));
Длина проекции отрезка на плоскость Х-Z:
Lxz = sqrt((x1-x2)*(x1-x2))+((z1-z2)*(z1-z2));
Длина отрезка Lxz = 58,309519;
Длина проекции отрезка на плоскость Х-Y:
Lxy = sqrt((x1-x2)*(x1-x2))+((y1-y2)*(y1-y2));
Длина отрезка Lxy = 50;
Углы между проекцией отрезка на плоскости и осью:
Угол между осью Х-Х и проекцией отрезка на плоскость X-Y.
Uxy = arctan((y2-y1)/(x2-x1)); Uxy = 53,130102354…
Угол между осью Х-Х и проекцией отрезка на плоскость X-Z.
Uxz = arctan((z2-z1)/(x2-x1)); Uxz = 59,036243468…
Угол между осью Y-Y и проекцией отрезка на плоскость Y-Z.
Uyz = arctan((z2-z1)/(y2-y1)); Uyz = 51,340191746…
Определяем угол между плоскостью и отрезком в пространстве.
Угол между плоскостью X-Y и отрезком.
ULxy = arctan((z2-z1)/Lxy); ULxy = 45,0…
Угол между плоскостью X-Z и отрезком в пространстве.
ULxz = arctan((y2-y1)/Lxz); ULxz = 34,44990199…
Угол между плоскостью Y-Z и отрезком в пространстве.
ULyz = arctan((x2-x1)/Lyz); ULyz = 25,104090250…
Расчет линейной интерполяции.
Линейная интерполяция применяется при работе с табличными данными.
Из таблицы имеем две взаимосвязанных пары значений какой то функции.
Необходимо вычислить ординату при значении абсциссы близком взятой из таблицы пары абсцисс.
Например: Абсцисса x1 = 10; Ордината y1 = 20;
Абсцисса x2 = 90; Ордината y2 = 180;
Необходимо вычислить Ординату Yx при Абсциссе Хх = 50;
Примечание: Абсцисса Хх может также быть немного больше
или меньше крайних значений известных табличных Абсцисс.

Расчет: RF-01.
Yy = (((y2-y1)*(Хx-x1)) / (x2-x1))+y1; Yy = (((180-20)*(50-10)) / (90-10))+20;
Yy = ( 6400 / 80 )+20; Yy = 100;
Расчет центра масс.
Исходные данные:
Масса первого тела М1 = 40;
Масса второго тела М2 = 60;
От оси до центра массы первого тела Х1 = 20;
От оси до центра массы второго тела Х2 = 50;

Расчет:
От оси до центра массы системы двух тел:
Рассчитываем как моменты масс относительно Оси отсчета. RF-02/
Xx=((m1*x1)+(m2*x2))/(m1+m2); Xx=((40 * 20 )+( 60 * 50 ))/( 40 + 60 ); Хх = 38 …
Суммарная масса системы двух тел:
M=m1+m2; M= 40 + 60; M= 100 …
Расчет геометрии многогранника.
Многогранник:
Описанный диаметр d.
Вписанный диаметр dv.
Ширина грани L.
Угол между вершинами U.
Исходные данные:
Описанный диаметр d = 100…
Вписанный диаметр dv = 80,90169943749474.
Число граней многогранника n = 5…

Расчет:
Половина угла на грань:
Ur = 180 / n; Ur = 180 / 5; Ur = 36…
Расчет при известном описанном диаметре.
Радиус описанного диаметра:
R=d / 2; R=100 / 2; R= 50…
Радиус вписанной окружности:
Rv=(d/2)*cos( Ur ); Rv= 50 * cos( 36 );
Rv= 40,45084972…
Вписанный диаметр:
.dv=Rv+Rv; .dv= 40,45084972 + 40,45084972;
.dv= 80,90169944…
Максимальный размер между вершинами:
X = d * ( cos ( 90 / n ))…
Ширина грани:
Sg= 2*(sqrt( R * R – Rv * Rv )); Sg= 2*(sqrt( 50 * 50 – 40,45084972 * 40,45084972 ));
Sg= 58,77852523…
Площадь многогранника:
S= ( Sg * Rv * n ) / 2; S= ( 58,77852523 * 40,45084972 * 5 ) / 2; S= 5944,103227…
Расчет геометрии коробовой кривой ( овала ).
Коробовая кривая – этой кривой можно с достаточной точностью заменить овальную кривую.
К примеру с помощью программы расчета геометрии коробовой кривой можно рассчитать геометрические размеры обжатого уплотнительного круглого резинового кольца.

Построение:
Задано:
Большая полуось ОА… ОА = ОP..
Малая полуось ОВ.
Алгоритм Расчета:
ОА = ОP.. Построением..
Построением: РВ = ОА – ОВ; ТВ = РВ..
АВ =sqrt( АО*АО + ОВ*ОВ ); АТ = АВ – ТВ; ХТ = АТ / 2;
Из подобия треугольников: АХ / АО = АE / АВ; отсюда:
АE = АХ*АВ / АО; аналогично: ВК = ( АХ + ВТ )* АВ / ВО;
ОE = ОА – АE; ОК = ВК – ОВ; ХВ = ХТ + ТВ = AX + BT;
Для расчета площади сечения коробовой кривой :
Большой радиус Rb = КВ; Зная стороны ВК и ХВ – находим угол сектора « W ».
Зная радиус Rb и угол сектора « W » – найдем площадь сектора.
Зная стороны ОК и ОE прямоугольного треугольника – найдем его площадь
и вычтем из площади сектора радиуса Rb.
Малый радиус Rm = EА; Зная угол « W » прямоугольного треугольника КХВ
определяем угол сектора малого радиуса как:
G = 90 – W; Далее: определим площадь сектора малого радиуса.
Площадь сечения коробовой кривой найдена.
Найдем диаметр круга равный по площади заданной коробовой кривой:
.d =sqrt( 4*S / Pii ); Где S – площадь заданной коробовой кривой.
Контрольный расчет:
Дано:
Большая ось = 80; Малая ось = 60;
Расчет:
Больший радиус = 50,0..
От оси до центра Б. радиуса = 20,0..
Меньший радиус = 25,0..
От оси до центра M. радиуса = 15,0..
Угол раствора Б. радиусов = 73,73979529168804..
Площадь ограниченная коробовой кривой = 3776,62456647;
Диам. Круга равной площади = 69,34369289;
Геометрия радиусной кривой.
Все расчеты по разным вариантам исходных данных:
Хорда L; Прогиб Н; Радиус R; Угол G.
Эти расчеты часто требуются для нахождения элементов детали имеющих форму сегмента окружности.
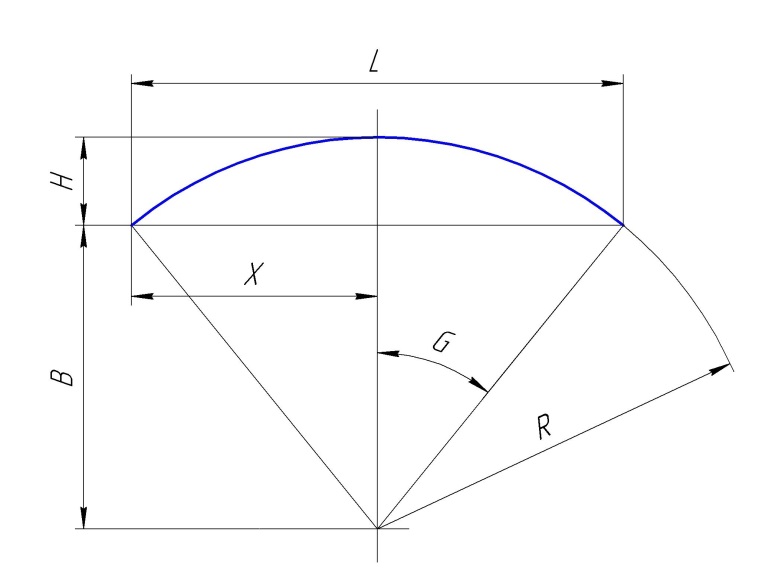
Расчет производим из следующих соотношений:
В = sqrt( R*R – X*X); L = X + X; H = R – B; G = аrcsin ( X / R );
Длина дуги = Pii * R * G / 90;
Площадь сектора Ss = Pii * R * R * G / 180;
Площадь треугольника под хордой St = L * B /2;
Площадь сегмента ( горбушки ) Sg = Ss – St;
Некоторые комбинации данных не позволяют прямого расчета,
тогда применяем метод компьютерного подбора.
Контрольный расчет:
Радиус R = 1000;
Диаметр D = R+R; D = 2000; Хорда L = 765,3668647;
Стрела прогиба максимальная H = 76,12046749;
Угол: Центр – Хорда: 2 * G = Au = 45 градусов..
Площадь сектора круга с углом = Au:
Sk=Pii*D*D* Au /(4*360); Sk = 392699,0816987241;
Площадь треугольника в секторе:
St=(L/2)* B; St = 353553,3905932738;
Площадь горбушки отсеченной хордой:
S = Sk-St; S = 39145,69110545033;
Длина дуги над хордой:
L=Pii*D*Au /360; L = 785,3981634;
Координаты радиусной кривой.
Построение части окружности методом подъема применяется тогда, когда радиус слишком велик
для традиционного построения, либо когда точка центра радиуса недоступна.

Построение части окружности методом подъема.
Построение:
Задаем максимальный размер хорды L.
Из середины максимальной хорды L строим перпендикуляр Н1.
Х1 = L / 2; В = sqrt( R*R – X1*X1); H1 = R – B;
Определили максимальную стрелу прогиба кривой H1.
Далее задаем произвольное расстояние от центральной оси Х2.
Находим стрелу прогиба Н2 = R – ( sqrt( R*R – X2*X2));
Находим высоту подъема в точке Х2: Hm = H1 – H2;
Задавая ряд текущих значений Х2 и рассчитывая соответствующие высоты подъема Hm
– получаем достаточное количество точек,
для построения радиусной кривой по точкам на этой кривой.
Контрольный расчет:
Исходные данные:
Радиус R = 10000;
Хорда максимальная заданная L = 8000;
Подъем максимальный в центре хорды = 834,8486100883201.
Задаем ряд точек:
От центра хорды до точки по оси Х-Х = 3000,0.
Величина подъема ( перпендикуляра ) = 374,2406242577763.
…
От центра хорды до точки по оси Х-Х = 2000,0.
Величина подъема ( перпендикуляра ) = 632,8075812210318.
…
От центра хорды до точки по оси Х-Х = 1000,0.
Величина подъема ( перпендикуляра ) = 784,7229811545203.
…
От центра хорды до точки по оси Х-Х = 500,0.
Величина подъема ( перпендикуляра ) = 822,3407878074104.
…
От центра хорды до точки по оси Х-Х = 0,001.
Величина подъема ( перпендикуляра ) = 834,848610088271.
Расчет геометрии треугольника.
Напротив сторон треугольника лежат одноименные углы.

Известны три стороны треугольника.
Напротив сторон треугольника лежат одноименные углы.
Сторона = a. Сторона = b. Сторона = c.
Решение:
.x=((b*b)+(c*c)-(a*a))/(2*b*c)… au=аrccos(x)… Угол А.
.x=((a*a)+(c*c)-(b*b))/(2*a*c)… bu=аrccos(x)… Угол В.
.cu=180-(au+bu)… Угол С.
....
Известны две стороны и угол между ними.
Сторона = a; Сторона = b; Угол = cu..
Решение:
.с= sqrt ((a*a)+(b*b))-(2*a*b*(cos(cu)))… Сторона « с ».
.x=((b*b)+(c*c)-(a*a))/(2*b*c)… au=arccos(x)… Угол А.
.x=((a*a)+(c*c)-(b*b))/(2*a*c)… bu=arccos(x)… Угол В.
..... .....
Известны два угла и сторона между ними.
Сторона = a; Угол = bu; Угол = cu;
Решение: .au=180-(bu+cu)… Угол А. .b=(a*(sin(bu)))/(sin(au))… Сторона В.
.c=(b*(sin(cu)))/(sin(bu))… Сторона С.
..... .....
Добавочный расчет в алгоритм Треугольника.
Решение:
R=a/(2*(sin(au))… R – Радиус описанной окружности.
.hc=b*(sin(au))… Высота из угла С.
.hb=a*( sin(cu))… Высота из угла B.
.ha=c*(sin(bu))… Высота из угла A.
S=a*ha/2.. Площадь треугольника.
Pe=a+b+c.. Периметр.
.rv=(S+S)/Pe… Радиус вписанной окружности.
…..
Контрольный расчет:
Напротив сторон треугольника лежат одноименные углы.
Сторона А = 15,77350269;
Сторона В = 14,14213562;
Сторона С = 11,54700538;
Угол А = 75; Угол В = 60; Угол С = 45..
Высота А= 10; Высота В = 11,1535507;
Высота С = 13,66025403;
Описанный радиус = 8,164965804;
Вписанный радиус = 3,804268442;
Площадь = 78,86751346;
……