Приборостроение - читать онлайн

5. Распределение случайных величин

Затрагивая вопрос о вероятности некоторого события, нельзя не говорить о закономерностях появления случайных величин.

Чтобы упростить ситуацию, эти величины делят на:

1) прерывные (дискретные) – например, количество некоторой продукции, не отвечающее установленным стандартам;

2) непрерывные – например, единицы той же продукции, которые имеют неодинаковые параметры, но эти параметры находятся в пределах границ предельно допустимого.

Зависимость между возможными значениями случайных величин и их вероятностями, выраженными конкретным способом, называется законом распределения случайных величин.

Для того, чтобы установить математическую форму этого закона, предположим, что дискретная случайная величина х может принимать значения х₁, x₂, x₃…, х_i…., x_k, и пусть каждому из этих значений соответствует вероятность P_x. Тогда ряд вероятностей, соответствующих значениям случайной величины х, будет иметь следующий вид P_x,P_x1,P_x2,…,P_xi,…,P_xk.

Очевидно, что вероятность P_x является некоторой функцией от переменной х и имеет вид: P_x = f(х), где x = x_i, i = 1, 2…, k.

Рассмотрим поведение этой функции для вышеприведенных двух видов случайных величин.

1. Случайная величина – дискретная (прерывная).

Случайная величина х < х', где х < х' задано, может выражаться следующим образом:

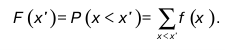
Функция F(х)=F(х') называется функцией распределения случайной прерывной величины ч. 2. Случайная величина – непрерывна. Плотностью вероятности P_x в точке X = х называется предел вида

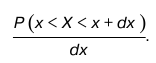
Следовательно, функцию F(х') можно дифференцировать, тогда

F (х)=f (х)

Основные свойства функции распределения следующие:

1) х = ∞;F(∞)= 1;

2) х = —∞;F(∞) = 0;

3) если аргумент x возрастает, т. е. если рассмотреть случай х₂ > х₁, то F(x₂) > F(x₁).

Если рассмотреть ΔF(х)=F(х₂)-F (х₁) то