Глава 1. Нейросеть

Создание умных машин

Мозг – самый невероятный орган. Именно он определяет, как мы воспринимаем всё, что видим, слышим, обоняем, пробуем на вкус и осязаем. Он позволяет хранить воспоминания, испытывать эмоции и даже мечтать. Без мозга мы были бы примитивными организмами, способными лишь на простейшие рефлексы. В целом он делает человека разумным.

Мозг ребенка весит меньше полукилограмма, но как-то решает задачи, пока недоступные даже самым большим и мощным компьютерам. Всего через несколько месяцев после рождения дети способны распознавать лица родителей, отделять объекты от фона и даже различать голоса. За первый год у них развивается интуитивное понимание естественной физики, они учатся видеть, где находятся частично или полностью скрытые от них объекты, и ассоциировать звуки с их значениями. Уже в раннем возрасте они на высоком уровне овладевают грамматикой, а в их словаре появляются тысячи слов[1].

Десятилетиями мы мечтаем о создании разумных машин с таким же мозгом, как у нас: роботов-помощников для уборки в доме; машин, которые управляют собой сами; микроскопов, автоматически выявляющих болезни. Но создание машин с искусственным интеллектом требует решения сложнейших вычислительных задач в истории, которые, однако, наш мозг способен раскусить в доли секунды. Для этого нужно разработать иной способ программирования компьютеров при помощи методов, которые появились в основном в последние десять лет. Это очень активная отрасль в исследованиях искусственного интеллекта, которая получила название глубокого обучения.

Ограничения традиционных компьютерных программ

Почему некоторые задачи компьютерам решать тяжело? Стандартные программы доказали свою состоятельность в двух областях: 1) они очень быстро ведут вычисления; 2) они неукоснительно следуют инструкциям. Если вы финансист и вам нужно провести сложные математические подсчеты, вам повезло. Типовые программы вам в помощь. Но представьте себе, что нам нужно сделать кое-что поинтереснее: например, написать программу для автоматического распознавания почерка. Возьмем за основу рис. 1.1.


Рис. 1.1. Изображение из массива рукописных данных MNIST[2]


Хотя каждая цифра на рисунке слегка отличается от предыдущей, мы легко опознаем в первом ряде нули, во втором – единицы и т. д. Теперь напишем компьютерную программу, которая решит ту же задачу. Какие правила нужно задать, чтобы различать цифры?

Начнем с простого. Например, укажем, что нулю соответствует изображение округлого замкнутого контура. Все примеры с рис. 1.1, кажется, удовлетворяют этому определению, но таких признаков недостаточно. Что, если у кого-то ноль – не всегда замкнутая фигура? И как отличить такой ноль (см. рис. 1.2) от шестерки?


Рис. 1.2. Ноль, алгоритмически трудноотличимый от шестерки


Можно задать рамки расстояния между началом и концом петли, но не очень понятно какие. И это только начало проблем. Как различить тройки и пятерки? Четверки и девятки? Можно добавлять правила, или признаки, после тщательных наблюдений и месяцев проб и ошибок, но понятно одно: процесс будет нелегок.

Многие другие классы задач попадают в ту же категорию: распознавание объектов и речи, автоматический перевод и т. д. Мы не знаем, какие программы писать для них, потому что не понимаем, как с этим справляется наш мозг. А если бы и знали, такая программа была бы невероятно сложной.

Механика машинного обучения

Для решения таких задач нужен совсем иной подход. Многое из того, что мы усваиваем в школе, похоже на стандартные компьютерные программы. Мы учимся перемножать числа, решать уравнения и получать результаты, следуя инструкциям. Но навыки, которые мы получаем в самом юном возрасте и считаем самыми естественными, усваиваются не из формул, а на примерах.

Например, в двухлетнем возрасте родители не учат нас узнавать собаку, измеряя форму ее носа или контуры тела. Мы можем отличать ее от других существ, потому что нам показали много примеров собак и несколько раз исправили наши ошибки. Уже при рождении мозг дал нам модель, описывающую наше мировосприятие. С возрастом благодаря ей мы стали на основе получаемой сенсорной информации строить предположения о том, с чем сталкиваемся. Если предположение подтверждалось родителями, это способствовало укреплению модели. Если же они говорили, что мы ошиблись, мы меняли модель, дополняя ее новой информацией. С опытом она становится все точнее, поскольку включает больше примеров. И так происходит на подсознательном уровне, мы этого даже не понимаем, но можем с выгодой использовать.

Глубокое обучение – отрасль более широкой области исследований искусственного интеллекта: машинного обучения, подразумевающего получение знаний из примеров. Мы не задаем компьютеру огромный список правил решения задачи, а предоставляем модель, с помощью которой он может сравнивать примеры, и краткий набор инструкций для ее модификации в случае ошибки. Со временем она должна улучшиться настолько, чтобы решать поставленные задачи очень точно.

Перейдем к более строгому изложению и сформулируем идею математически. Пусть наша модель – функция h(x, θ). Входное значение x – пример в векторной форме. Допустим, если x – изображение в оттенках серого, компоненты вектора – интенсивность пикселей в каждой позиции, как показано на рис. 1.3.


Рис. 1.3. Векторизация изображения для алгоритма машинного обучения


Входное значение θ – вектор параметров, используемых в нашей модели. Программа пытается усовершенствовать их значения на основе растущего числа примеров. Подробнее мы рассмотрим этот вопрос в главе 2.

Чтобы интуитивно понимать модели машинного обучения, рассмотрим пример. Допустим, мы решили узнать, как предсказывать результаты экзаменов, если известно количество часов сна и учебы в день перед испытанием. Мы собираем массив данных и при каждом замере х = [x1 x2]T записываем количество часов сна (x1), учебы (x2) и отмечаем, выше или ниже они средних по классу. Наша цель – создать модель h(х,θ) с вектором параметров θ = [θ0 θ1 θ2]T, чтобы:



По нашему предположению, проект модели h(х,θ) будет таким, как описано выше (с геометрической точки зрения он описывает линейный классификатор, делящий плоскость координат надвое). Теперь мы хотим узнать вектор параметров θ, чтобы научить модель делать верные предсказания (−1, если результаты ниже среднего уровня, и 1 – если выше) на основании примерного входного значения x. Такая модель называется линейным персептроном и используется с 1950-х[3]. Предположим, наши данные соответствуют тому, что показано на рис. 1.4.


Рис. 1.4. Образец данных для алгоритма предсказания экзаменов и потенциального классификатора


Оказывается, при θ = [−24 3 4]T модель машинного обучения способна сделать верное предсказание для каждого замера:



Оптимальный вектор параметров θ устанавливает классификатор так, чтобы можно было сделать как можно больше корректных предсказаний. Обычно есть множество (иногда даже бесконечное) возможных оптимальных вариантов θ. К счастью, в большинстве случаев альтернативы настолько близки, что разницей между ними можно пренебречь. Если это не так, можно собрать больше данных, чтобы сузить выбор θ.

Звучит разумно, но есть много очень серьезных вопросов. Во-первых, откуда берется оптимальное значение вектора параметров θ? Решение этой задачи требует применения метода оптимизации. Оптимизаторы стремятся повысить производительность модели машинного обучения, последовательно изменяя ее параметры, пока погрешность не станет минимальной.

Мы подробнее расскажем об обучении векторов параметров в главе 2, описывая процесс градиентного спуска[4]. Позже мы постараемся найти способы еще больше увеличить эффективность этого процесса.

Во-вторых, очевидно, что эта модель (линейного персептрона) имеет ограниченный потенциал обучения. Например, случаи распределения данных на рис. 1.5 нельзя удобно описать с помощью линейного персептрона.


Рис. 1.5. По мере того как данные принимают более комплексные формы, нам становятся необходимы более сложные модели для их описания


Но эти ситуации – верхушка айсберга. Когда мы переходим к более комплексным проблемам – распознаванию объектов или анализу текста, – данные приобретают очень много измерений, а отношения, которые мы хотим описать, становятся крайне нелинейными. Чтобы отразить это, в последнее время специалисты по машинному обучению стали строить модели, напоминающие структуры нашего мозга. Именно в этой области, обычно называемой глубоким обучением, ученые добились впечатляющих успехов в решении проблем компьютерного зрения и обработки естественного языка. Их алгоритмы не только значительно превосходят все остальные, но даже соперничают по точности с достижениями человека, а то и превосходят их.

Нейрон

Нейрон – основная единица мозга. Небольшой его фрагмент, размером примерно с рисовое зернышко, содержит более 10 тысяч нейронов, каждый из которых в среднем формирует около 6000 связей с другими такими клетками[5]. Именно эта громоздкая биологическая сеть позволяет нам воспринимать мир вокруг. В этом разделе наша задача – воспользоваться естественной структурой для создания моделей машинного обучения, которые решают задачи аналогично. По сути, нейрон оптимизирован для получения информации от «коллег», ее уникальной обработки и пересылки результатов в другие клетки. Процесс отражен на рис. 1.6. Нейрон получает входную информацию по дендритам – структурам, напоминающим антенны. Каждая из входящих связей динамически усиливается или ослабляется на основании частоты использования (так мы учимся новому!), и сила соединений определяет вклад входящего элемента информации в то, что нейрон выдаст на выходе. Входные данные оцениваются на основе этой силы и объединяются в клеточном теле. Результат трансформируется в новый сигнал, который распространяется по клеточному аксону к другим нейронам.


Рис. 1.6. Функциональное описание биологической структуры нейрона


Мы можем преобразовать функциональное понимание работы нейронов в нашем мозге в искусственную модель на компьютере. Последняя описана на рис. 1.7, где применен подход, впервые введенный в 1943 году Уорреном Маккаллоу и Уолтером Питтсом[6]. Как и биологические нейроны, искусственный получает некоторый объем входных данных – x1, x2, …, xn, каждый элемент которых умножается на определенное значение веса – w1, w2, …, wn. Эти значения, как и раньше, суммируются, давая логит нейрона: . Часто он включает также смещение (константа, здесь не показана). Логит проходит через функцию активации f, образуя выходное значение y = f(z). Это значение может быть передано в другие нейроны.


Рис. 1.7. Схема работы нейрона в искусственной нейросети


Математическое обсуждение искусственного нейрона мы закончим, выразив его функции в векторной форме. Представим входные данные нейрона как вектор x = [x1 x2 … xn], а веса нейрона как w = [w1 w2 … wn]. Теперь выходные данные нейрона можно выразить как y = f (x w + b), где b – смещение. Мы способны вычислить выходные данные из скалярного произведения входного вектора на вектор весов, добавив смещение и получив логит, а затем применив функцию активации. Это кажется тривиальным, но представление нейронов в виде ряда векторных операций очень важно: только в таком формате их используют в программировании.

Выражение линейных персептронов в виде нейронов

Выше мы говорили об использовании моделей машинного обучения для определения зависимости между результатом на экзаменах и временем, потраченным на обучение и сон. Для решения задачи мы создали линейный классификатор-персептрон, который делит плоскость декартовых координат надвое:



Как показано на рис. 1.4, это оптимальный вариант для θ: он позволяет корректно классифицировать все примеры в нашем наборе данных. Здесь мы видим, что наша модель h работает по образцу нейрона. Посмотрите на нейрон на рис. 1.8. У него два входных значения, смещение, и он использует функцию:



Рис. 1.8. Выражение результатов экзамена в виде нейрона


Легко показать, что линейный персептрон и нейронная модель полностью эквивалентны. И просто продемонстрировать, что одиночные нейроны более выразительны, чем линейные персептроны. Каждый из них может быть выражен в виде одиночного нейрона, но последние могут также отражать модели, которые нельзя выразить с помощью линейного персептрона.

Нейросети с прямым распространением сигнала

Одиночные нейроны мощнее линейных персептронов, но не способны решить сложные проблемы обучения. Поэтому наш мозг состоит из множества нейронов. Например, при помощи одного из них невозможно различить написанные от руки цифры. И чтобы решать более сложные задачи, нам нужны модели машинного обучения.

Нейроны в человеческом мозге расположены слоями. Его кора, по большей части отвечающая за интеллект, состоит из шести слоев. Информация перетекает по ним, пока сенсорные данные не преобразуются в концептуальное понимание[7]. Например, самый нижний слой визуальной зоны коры получает необработанные визуальные данные от глаз. Эта информация преобразуется в каждом следующем слое и передается далее, пока на шестом слое мы не заключаем, что видим кошку, банку газировки или самолет. На рис. 1.9 показан упрощенный вариант этих слоев.


Рис. 1.9. Простой пример нейросети с прямым распространением сигнала с тремя слоями (входной, скрытый, выходной) и тремя нейронами на каждый слой


На основе этих идей мы можем создать искусственную нейросеть. Она возникает, когда мы начинаем соединять нейроны друг с другом, со входными данными и выходными узлами, которые соответствуют ответам сети на изучаемую задачу. На рис. 1.9 показан простейший пример искусственной нейросети, схожей по архитектуре с той, что была описана в 1943 году в работе Маккаллоу и Питтса. В нижний слой поступают входные данные. Верхний (выходные узлы) вычисляет ответ. Средний слой (слои) нейронов именуется скрытым, и здесь 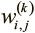– вес соединения i-го нейрона в k-м слое с j-м нейроном в (k + 1) – м слое. Эти веса образуют вектор параметров θ, и, как и ранее, наша способность решать задачи при помощи нейросетей зависит от нахождения оптимальных значений для θ.

В этом примере соединения устанавливаются только от нижних слоев к верхним. Отсутствуют связи между нейронами одного уровня, нет таких, которые передают данные от высшего слоя к низшему. Подобные нейросети называются сетями с прямым распространением сигнала, и мы начнем с них, потому что их анализировать проще всего. Такой разбор (процесс выбора оптимальных значений для весов) мы предложим в главе 2. Более сложные варианты связей будут рассмотрены в дальнейших главах.

Ниже мы рассмотрим основные типы слоев, используемые в нейросетях с прямым распространением сигнала. Но для начала несколько важных замечаний.

1. Как мы уже говорили, слои нейронов между первым (входным) и последним (выходным) слоями называются скрытыми. Здесь в основном и происходят волшебные процессы, нейросеть пытается решить поставленные задачи. Раньше (как при распознавании рукописных цифр) мы тратили много времени на определение полезных свойств; эти скрытые слои автоматизируют процесс. Рассмотрение процессов в них может многое сказать о свойствах, которые сеть научилась автоматически извлекать из данных.

2. В этом примере у каждого слоя один набор нейронов, но это не необходимое и не рекомендуемое условие. Чаще в скрытых слоях нейронов меньше, чем во входном: так сеть обучается сжатому представлению информации. Например, когда глаза получают «сырые» пиксельные значения, мозг обрабатывает их в рамках границ и контуров. Скрытые слои биологических нейронов мозга заставляют нас искать более качественное представление всего, что мы воспринимаем.

3. Необязательно, чтобы выход каждого нейрона был связан с входами всех нейронов следующего уровня. Выбор связей здесь – искусство, которое приходит с опытом. Этот вопрос мы обсудим детально при изучении примеров нейросетей.

4. Входные и выходные данные – векторные представления. Например, можно изобразить нейросеть, в которой входные данные и конкретные пиксельные значения картинки в режиме RGB представлены в виде вектора (см. рис. 1.3). Последний слой может иметь два нейрона, которые соотносятся с ответом на задачу: [1, 0], если на картинке собака; [0, 1], если кошка; [1, 1], если есть оба животных; [0, 0], если нет ни одного из них.

Заметим, что, как и нейрон, можно математически выразить нейросеть как серию операций с векторами и матрицами. Пусть входные значение i-го слоя сети – вектор x = [x1 x2 … xn]. Нам надо найти вектор y = [y1 y2 … ym], образованный распространением входных данных по нейронам. Мы можем выразить это как простое умножение матрицы, создав матрицу весов размера n × m и вектор смещения размера m. Каждый столбец будет соответствовать нейрону, причем j-й элемент сопоставлен весу соединения с j-м входящим элементом. Иными словами, y = ƒ(WTx + b), где функция активации применяется к вектору поэлементно. Эта новая формулировка очень пригодится, когда мы начнем реализовывать эти сети в программах.

Линейные нейроны и их ограничения

Большинство типов нейронов определяются функцией активации f, примененной к логиту logit z. Сначала рассмотрим слои нейронов, которые используют линейную функцию f(z) = az + b. Например, нейрон, который пытается подсчитать стоимость блюда в кафе быстрого обслуживания, будет линейным, a = 1 и b = 0. Используя f(z) = z и веса, эквивалентные стоимости каждого блюда, программа присвоит линейному нейрону на рис. 1.10 определенную тройку из бургеров, картошки и газировки, и он выдаст цену их сочетания.


Рис. 1.10. Пример линейного нейрона


Вычисления с линейными нейронами просты, но имеют серьезные ограничения. Несложно доказать, что любая нейросеть с прямым распространением сигнала, состоящая только из таких нейронов, может быть представлена как сеть без скрытых слоев. Это проблема: как мы уже говорили, именно скрытые слои позволяют узнавать важные свойства входных данных. Чтобы научиться понимать сложные отношения, нужно использовать нейроны с определенного рода нелинейностью.

Нейроны с сигмоидой, гиперболическим тангенсом и усеченные линейные

На практике для вычислений применяются три типа нелинейных нейронов. Первый называется сигмоидным и использует функцию:



Интуитивно это означает, что, если логит очень мал, выходные данные логистического нейрона близки к 0. Если логит очень велик – то к 1. Между этими двумя экстремумами нейрон принимает форму буквы S, как на рис. 1.11.


Рис. 1.11. Выходные данные сигмоидного нейрона с переменной z


Нейроны гиперболического тангенса (tanh-нейроны) используют похожую S-образную нелинейность, но исходящие значения варьируют не от 0 до 1, а от −1 до 1. Формула для них предсказуемая: f(z) = tanh(z). Отношения между входным значением y и логитом z показаны на рис. 1.12. Когда используются S-образные нелинейности, часто предпочитают tanh-нейроны, а не сигмоидные, поскольку у tanh-нейронов центр находится в 0.


Рис. 1.12. Выходные данные tanh-нейрона с переменной z


Еще один тип нелинейности используется нейроном с усеченным линейным преобразованием (ReLU). Здесь задействована функция f(z) = max(0, z), и ее график имеет форму хоккейной клюшки (рис. 1.13).


Рис. 1.13. Выходные данные ReLU-нейрона с переменной z


ReLU в последнее время часто выбирается для выполнения многих задач (особенно в системах компьютерного зрения) по ряду причин, несмотря на свои недостатки[8]. Этот вопрос мы рассмотрим в главе 5 вместе со стратегиями борьбы с потенциальными проблемами.

Выходные слои с функцией мягкого максимума

Часто нужно, чтобы выходной вектор был распределением вероятностей по набору взаимоисключающих значений. Допустим, нам нужно создать нейросеть для распознавания рукописных цифр из набора данных MNIST. Каждое значение (от 0 до 9) исключает остальные, но маловероятно, чтобы нам удалось распознать цифры со стопроцентной точностью. Распределение вероятностей поможет понять, насколько мы уверены в своих выводах. Желаемый выходной вектор приобретает такую форму, где :

[p0 p1 p2 p3 … p9].

Для этого используется особый выходной слой, именуемый слоем с мягким максимумом (softmax). В отличие от других типов, выходные данные нейрона в слое с мягким максимумом зависят от выходных данных всех остальных нейронов в нем. Нам нужно, чтобы сумма всех выходных значений равнялась 1. Приняв zi как логит i-го нейрона с мягким максимумом, мы можем достичь следующей нормализации, задав выходные значения:



При сильном предсказании одно из значений вектора будет близко к 1, остальные – к 0. При слабом останется несколько возможных значений, каждое из которых характеризуется своим уровнем вероятности.

Резюме

В этой главе мы дали базовые представления о машинном обучении и нейросетях. Мы рассказали о структуре нейрона, работе нейросетей с прямым распространением сигнала и важности нелинейности в решении сложных задач обучения. В следующей главе мы начнем создавать математический фундамент для обучения нейросети решению задач. Например, мы поговорим о нахождении оптимальных векторов параметров, лучших методов обучения нейросетей и основных проблемах. В последующих главах мы будем применять эти основополагающие идеи к более специализированным вариантам архитектуры нейросетей.