Население Земли как растущая иерархическая сеть - читать онлайн

Как известно, в любой науке столько истины – сколько в ней математики. Предлагаемая здесь теория описывает гиперболический рост населения мира на языке математики. Язык этот тяжел для восприятия, поэтому автор настоятельно рекомендует при первом чтении лишь просмотреть математические выкладки. Прочитать нужно только «Основные определения» и «Выводы по растущим иерархическим сетям».

Математика здесь несложная, но необычная; автор не знает аналогов, хотя, возможно, они и существуют. Все вставки – работающие листинги из системы MathCAD, так что тем, кто умеет с ней работать – легко все проверить.

Основные определения

Сетью называется граф, в котором вершины (узлы) соединены между собой связями, в данном случае двунаправленными (изображаемые ненаправленными) отрезками. Сеть, в которой каждый узел связан с каждым, называется гипертетраэдральной, а граф, обладающий таким свойством, – полным. (Только такие сети здесь и будем рассматривать.) Число связей, исходящих из одного узла, на единицу меньше числа узлов. Общее число связей S = N(N – 1)/2, например, сеть из пяти узлов содержит десять связей:

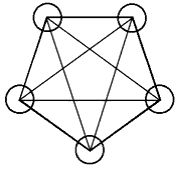
Рис. 1. Сеть, содержащая пять узлов; число связей S = 5·4/2 = 10.

Узлы сети могут быть соединены связями как непосредственно, так и через магистральный узел. Магистральный узел сети – это узел, к которому сходятся все связи растущей сети. Сеть, в которой число узлов равно 2^R назовем гармонической, например, сеть из восьми узлов:

Рис. 2. Гармоническая сеть, содержащая 8 узлов; число связей равно 28.

Совершенной сетью назовем гармоническую сеть, содержащую число узлов, равное:

Где R – это ранг сети. Примеры совершенных сетей:

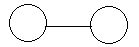
Рис. 3. R = 0, сеть содержит 2 узла, число связей равно единице.

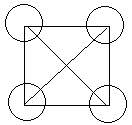
Рис. 4. R = 1, сеть содержит 4 узла, число связей равно шести.

Рис. 5. R = 2, сеть содержит 16 узлов, число связей равно 120.

Дадим рекурсивное определение совершенной иерархической сети (СИС). Совершенной иерархической сетью ранга R будем называть такую совершенную сеть ранга R, вершиной которой является СИС ранга R − 1. Эту сеть с рангом равным R − 1 назовем сетеобразующим клаттером сети ранга R. Магистральный узел клаттера – это узел, к которому сходятся связи от магистральных узлов клаттеров на единицу меньшего ранга, составляющих данный клаттер. (Один из узлов-носителей каждого клаттера берет на себя функцию магистрального узла этого клаттера.)

Таким образом каждому узлу СИС сопоставляется также СИС, но на единицу меньшего ранга. Спускаясь по этой лестнице вниз, дойдем до первого этажа, точнее подвала (R = 0) в этой метафоре (если отождествлять ранг с этажом), который назовем уровнем носителя.

Чтобы рекурсия заработала дополнительно определим СИС ранга нуль как СИС, которая состоит из двух узлов, соединенных связью, которые назовем носителями. Под носителем при таком определении также понимается СИС (клаттер), но СИС эта не представляется в данной упрощенной модели как вершина иерархии сетей меньшего ранга, а рассматривается лишь как наименьшая, неделимая далее и не имеющая ранга структурная единица иерархической сети.

Узел-носитель (клаттер-носитель) есть величина постоянная; он обеспечивает функционирование сети и ее эволюцию. Чтобы связать сеть и мировую демографию будем считать, что этот узел-носитель не может существовать без своего «двойника», носителя-человека. Носитель-человек – это живущий и обладающий сознанием человек, временно «прикрепленный» к узлу-носителю сети и постоянно сменяющийся в процессе ее роста. Далее, для краткости изложения и в зависимости от контекста, будем называть единство узла-носителя и связанного с ним носителя-человека – носителем сети или просто носителем. Принимаем также, что связь самого нижнего уровня подключается к каждому узлу-носителю и к магистральному узлу клаттера ранга нуль, причем узел-носитель может поддерживать только одну такую связь.

Каждый узел-носитель рассматривается как уникальный, отличный от других носителей, клаттер сети ранга нуль. Выделенность носителя среди прочих СИС заключается в том, что рост сети любого ранга происходит путем копирования ее носителей (см. далее)[26].

Ранг СИС может принимать в данной модели следующие значения: R = 0, 1, 2… СИС минимального ранга – ранга нуль – это тот кирпичик, из которого строятся все остальные иерархические сети:

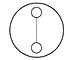
Рис. 6. СИС ранга нуль, R = 0.

Рис. 7. СИС ранга один, R = 1.

Рис. 8. СИС ранга два, R = 2.

Число клаттеров СИС равно числу носителей в ее клаттере (рис. 8). Гармонической иерархической сетью (ГИС) ранга R назовем такую иерархическую сеть, каждым клаттером которой является СИС ранга R, а число этих клаттеров равно двойке в некоторой степени: 2ⁿ, n = 1, 2… R – 1. Всякая СИС является так же и ГИС.

Если же число клаттеров иерархической сети не равно 2ⁿ, то такую сеть назовем несовершенной или просто иерархической сетью (ИС) ранга R[27]. Вес клаттера P определим как число носителей, которое он содержит:

Рис. 9. Вес клаттера сети ранга R.

Магистральный узел ИС/клаттера – это узел, к которому сходятся все связи от магистральных узлов слагающих ее/его клаттеров. Размер сети L – это число клаттеров, которое она содержит. Число носителей ИС равно произведению веса клаттера на ее размер: N = PL. Число носителей СИС равно квадрату веса ее клаттера: N_s = P². Пример:

Рис. 10. ИС ранга 3, размером в три клаттера, вес каждого равен 256, число носителей 256·3 = 768. (Клаттеры для наглядности связаны непосредственно, а не через магистральный узел.)

Здесь мы дали определение биниальной иерархической сети (БИС), т. е. сети, клаттером которой является совершенная биниальная иерархическая сеть на единицу меньшего ранга. Теоретически можно рассмотреть тринитарную иерархическую сеть или даже сети более высокого порядка. Но, как утверждают сторонники биниальной парадигмы, приводя тому многочисленные примеры, именно дихотомическая (парная) структура прослеживается на всех иерархических уровнях организации макро и микромира.

Иначе говоря, все существующие природные объекты обнаруживают парность (биниальность, от лат. bini – пара), когда единое целое (атом, живая клетка, планета, звезда и т. д.) состоит только из двух частей (бинитаксонов), каждая из которых на нижеследующем иерархическом уровне вновь делится на две составляющие и т. д. Именно поэтому простейшая из возможных иерархических сетей, сеть минимального порядка, биниальная иерархическая сеть (в дальнейшем просто иерархическая сеть) лучше всего отвечает биниальной парадигме.

Далее, мы рассмотрим растущую, т. е. увеличивающую свой размер, а затем и ранг ИС и подберем для нее такой алгоритм роста, который наилучшим образом отвечает идее эволюции.

Растущая иерархическая сеть

Растущая ИС – это сеть, число клаттеров которой растет согласно некоторому алгоритму. Этот рост будем связывать с операцией самокопирования ИС, которая происходит циклически. Цикл самокопирования ИС определим как такой этап ее роста, на котором копируются все (в произвольном порядке и без повторения) клаттеры, имеющиеся в ней к моменту входа в этот цикл[28]. Звено самокопирования ИС определим как такую последовательность клаттеров, на которой собирается и устанавливается в сеть еще один новый клаттер. Длина звена Z – это количество клаттеров, входящих в звено.

Операция самокопирования заключается в следующем: ИС последовательно (клаттер за клаттером) копирует носителями по определенному правилу текущее число клаттеров[29], собирает новый, устанавливает его в себя и увеличивает свой размер на единицу. Правило самокопирования выберем таким:

Новый клаттер собирается в процессе копирования носителями связей каждого клаттера и его магистрального узла. Т. е. (чисто схематически) копируется магистральный узел сетеобразующего клаттера[30] и каждая входящая в него связь. Можно сформулировать иначе: с каждого сетеобразующего клаттера в текущем цикле копируется и устанавливается в собираемый клаттер число носителей, равное текущему размеру сети[31].

Клаттеры, собранные внутри цикла на втором этапе роста сети (см. далее), в очередь на копирование в текущем цикле не ставятся. Процесс копирования клаттеров на всех этапах роста сети можно представить следующим образом: сначала создается копия магистрального узла клаттера и соединяется с магистральным узлом растущей сети. Затем копируются магистральные узлы клаттеров нижнего уровня, составляющих копируемый клаттер, и только после этого последовательно копируются все остальные узлы (носители) и через магистральные узлы клаттеров нижнего уровня подключаются к магистральному узлу собираемого клаттера. При таком сценарии каждый вновь поступающий носитель оказывается сразу же подключенным ко всей сети.

Почему выбирается именно такой алгоритм? В соответствии с системным подходом сложность, эволюционная зрелость любой развивающейся системы определяется, прежде всего, ее связями. Если связи растущей системы однородны, то скорость ее эволюции (в простейшем случае роста) зависит только от их числа. Чем больше связей – тем быстрее эволюционирует, развивается, растет система.

Поэтому логично постулировать, что прирост клаттеров-носителей с каждого сетеобразующего клаттера, получаемый в процессе его копирования, должен быть пропорционален, а в простейшем случае просто равен числу его связей с другими клаттерами. И в этом простейшем случае оказывается, что алгоритм хорошо описывает рост Сети человека на втором этапе (см. далее) и, соответственно, гиперболический рост населения мира после неолита.

Но если применить его при описании роста сети на первом этапе (см. далее) и, соответственно, роста численности первых архантропов, то получим, что положение циклов эволюции на оси времени и время появления рода Homo, рассчитанные теоретически, не согласуются с данными палеодемографии.

Однако, если слегка модифицировать алгоритм так, чтобы при подсчете прироста носителей с каждого клаттера добавлять к числу его связей единицу, формально полагая, что копируются не только входящие в клаттер связи, но и его магистральный узел (т. е., если считать, что число копий клаттеров-носителей, снимаемых с каждого сетеобразующего клаттера за цикл, равно текущему размеру сети), что совершенно несущественно на втором этапе, когда таких клаттеров и, соответственно, подключенных к ним связей сотни, тысячи и даже десятки тысяч – то вот такой алгоритм будет правильно описывать эволюцию, историю и рост населения мира на всех этапах[33].

Дополнительно хотелось бы отметить, что выбранный алгоритм при учете правила финализации звена и цикла (которое, хотя и может быть сформулировано по-разному, но не оказывает практически никакого влияния на результат) хорош уже тем, что чрезвычайно прост и эстетичен.

Даже если бы оказалось, что он не имеет никакого отношения к реальному росту населения Земли, модель все равно заслуживала бы внимания уже только потому, что при минимальных предпосылках позволяет правильно описывать как количественно, так и качественно динамику роста (начало роста, неолит, переход), а также цикличность глобального развития: сокращающиеся по закону прогрессии циклы эволюции, глобальные исторические и экономические циклы.

В таком случае модель можно было бы рассматривать как простую и эффективную схему, позволяющую систематизировать многочисленные демографические и исторические данные. Но вопросов о том, почему это стало возможным, почему такая простая модель столь точно соответствует действительности, почему она вмещает в себя такой большой объем информации, случайно ли? – все равно не избежать.

Применим данный алгоритм для описания роста биниальной иерархической сети ранга R. Будем считать, что рост этот всегда начинается с двух клаттеров. В таком случае его можно разбить на три качественно отличающихся этапа:

Первый этап (√P < Z ≤ P/2) – рост от двух до √P клаттеров. (P = 2^(2^R) – вес клаттера или число носителей, которое он содержит. Z – длина звена копирования или число клаттеров, в процессе копирования которых собирается очередной дочерний клаттер.)

Второй этап (1 < Z ≤ √P) – рост от √P до Р клаттеров. На втором этапе новоиспеченные клаттеры в сеть включаются в процессе их сборки, но в текущем цикле в очередь на копирование не ставятся, копируются только подключенные к ним связи[10].

Третий этап (Z = 1) – операция репликации: создание одной копии полученной совершенной сети[9].

На первом этапе звено состоит из повторяющихся циклов, причем каждое последующее звено короче предыдущего; на втором этапе – цикл состоит из некоторого числа укорачивающихся звеньев. Длина звена за весь период роста уменьшается от P/2 до единицы.

Рассмотрим теперь все этапы роста ИС на примере сети ранга 3. Вес клаттера Р = 2^(2^3) = 2⁸ = 256, т. е. число носителей в клаттере равно 256. Корень из веса √Р = 16. Стартовый размер сети полагаем равным двум.

Рис. 1. Старт роста сети 256.

Алгоритм копирования следующий: на каждую связь и на каждый магистральный узел копируемого клаттера устанавливается носитель. Связи клаттера соединяют все другие его узлы с магистральным, а тот, в свою очередь, соединен с магистральным узлом сети. Но в приведенных схемах для наглядности будем изображать связи отрезками, соединяющими клаттеры. Кроме того, будем безо всякого ущерба для математики считать, что собираемый клаттер не подключен к сети и устанавливается в нее лишь в момент его полной сборки.

В данном случае связь одна, магистральный узел всегда один. Всего на клаттере копируем два носителя. Нужно собрать 256 носителей, поэтому переходим к следующему клаттеру и копируем еще два носителя.

Собрали четыре носителя. Цикл закончился, он оказался пустым, т. к. все имеющиеся на момент входа в цикл клаттеры скопированы, а новый собрать не удалось. Всего имеем 63 пустых цикла. На 64-м цикле и 128-ой по счету операции копирования (длина звена составила 128 клаттеров) получаем 256 носителей. Сборка клаттера завершена; устанавливаем его в сеть, прокладываем связи.

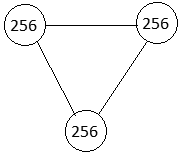
Рис. 2. Собран первый клаттер.

Теперь каждый клаттер имеет уже две входящие в него связи, поэтому копируем по три носителя на клаттере или 3² = 9 девять за цикл. Число 256 не делится нацело на 9, как в предыдущем случае, и для создания четвертого клаттера потребуется 256/9 = 28 полных циклов, плюс 4/9 цикла; поэтому последний 29-й цикл будет неполным, т. к. первый клаттер на нем будет скопирован полностью (3 носителя), второй – частично (один носитель), а третий – останется нескопированным. И здесь возникает неопределенность в вопросе как начинать следующее звено: с продолжения предыдущего неполного цикла или с начала нового?

Непонятно также следует ли учитывать неполный цикл при подсчете общего числа циклов звена. Ведь в приложении этой математической модели к росту населения Земли наиболее важными законами роста являются закон постоянства времени цикла и синхронности (синфазности) роста и развития. Неясно, правда, должна ли такая синхронность (синфазность) роста строго выполняться для каждого цикла или только для моментов гармонического достижения; а может быть синхронно должен завершаться только последний цикл роста сети данного ранга, на момент окончания которого она становится совершенной? (Учитывая факт гиперболического роста населения мира, этот вариант вряд ли следует принимать во внимание.)

Если считать, что каждое следующее звено начинается с нового цикла, что представляется наиболее логичным, то время роста сети в приложении этой математики к процессу эволюции может быть выражено только целым числом циклов. В таком случае определение цикла как операции самокопирования сети, при которой единожды копируются все клаттеры, имеющиеся в наличии в момент входа в цикл, должно быть расширено. А именно: некоторые такие операции, завершающие звено (или находящиеся внутри него[11]), могут быть неполными или избыточными и тем не менее такие операции должны считаться циклами.

Возвратимся теперь к нашему примеру, сколько все-таки следует взять циклов: 28 или 29?

Здесь возможны четыре варианта. 1) По минимуму: отдаем остаток 4 носителя 28-му циклу (т. е. копируем с последнего клаттера 28-го цикла дополнительно еще какие-то четыре носителя), или распределяем его по каким-то предыдущим, при этом получаем 28 циклов, на некоторых из которых будет скопировано более девяти носителей; т. е. носители некоторых клаттеров (возможно[12]) будут скопированы дважды. 2) По максимуму: добавляем еще один 29-й цикл и переносим в него весь остаток, при этом некоторые носители оказываются в последнем цикле звена нескопированными. 3) Этот вариант среднее между первым и вторым: если остаток меньше или равен половине квадрата размера сети (3²/2 = 4,5) выбирается первый вариант, в противном случае – второй[13].

Возможен также вариант с перехлестом», при котором звено копирования замыкается не в момент завершения цикла, а где-то у него внутри. После прокладки дополнительной связи следующее звено начинается с завершения предыдущего цикла т. е. с копирования нескопированных носителей заключительного цикла предыдущего звена (плюс один носитель с дополнительной связи)[14][15][16].

При подсчете числа циклов роста сети до совершенной (и числа циклов роста ее до каждого гармонического размера) все рассмотренные сценарии финализации звена дают практически одинаковый результат. Для определенности выбираем второй вариант, получаем 29 циклов. Собираем второй клаттер, устанавливаем в сеть, прокладываем связи.

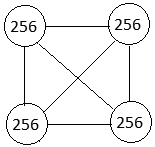
Рис. 3. Собран второй клаттер.

Далее, на каждом клаттере копируем по 4 носителя; за цикл их набирается 16. Третий клаттер собираем за 16 циклов, т. к. 16·16 = 256. Длина звена 16·4 = 64 клаттера.

Рис. 4. Собран третий клаттер.

Пять носителей на клаттер, 25 – с цикла; всего потребуется 11 циклов по второму сценарию и т. д.

На 13-ом по счету звене копирования сети и при L = 15 для сборки нового клаттера потребуется два цикла, поскольку первый цикл будет пустым: 15·15 = 225 < 256. С 14-го звена начинается второй этап роста сети. Теперь клаттер можно собрать не выходя за пределы одного цикла: 16·16 = 256.

Рис. 5. Собрано 16 клаттеров.

Рис. 6. Звено копирования фрагмента сети 256 по первому варианту.

Прирост клаттеров за цикл с этого момента при постоянстве времени цикла идет уже по другой, как мы покажем далее, гораздо более быстрой гиперболе. Т. е. процесс роста сети претерпевает качественный скачок. Допустим, что сеть выросла до размера 71, т. е. содержит 71 клаттер. Для фрагмента сети, изображенного на рисунке, имеем следующее: после копирования четырех клаттеров (Z = 4) получаем (70 + 1)·4 = 284 носителя. Здесь, так же как на первом этапе роста, возможны первые три варианта финализации звена: по минимуму, по максимуму и средний между первым и вторым. Длина звена равна четырем (по первому варианту).

После установки собранного клаттера в сеть число связей возрастает на единицу, и в процессе эволюции сети происходит качественный скачок. Поскольку длительность звена, в отличие от длительности цикла, в приложении этой модели к явлению роста населения Земли, не является постоянной, процесс ее уменьшения может идти с небольшими отклонениями. В таком случае для второго этапа должен быть рассмотрен еще один, четвертый вариант сценария финализации звена, а именно: с перехлестом, когда следующее звено начинается с копирования нескопированных носителей последнего клаттера предыдущего звена.

Рис. 7. Звено копирования фрагмента сети 256 с перехлестом.

Выбираем один из рассмотренных четырех вариантов финализации звена, собираем новый клаттер, устанавливаем в сеть, увеличиваем число связей на единицу (71). Алгоритм роста на втором этапе необходимо дополнить правилом финализации цикла, сходным с правилом финализации звена[17]:

1. Копируются клаттеры, которые имеются в сети, по одному из рассмотренных вариантов финализации звена. Как только новый клаттер из оставшихся на копирование в завершающем звене цикла по сумме позиций собрать не удается – цикл завершается. При этом остаются нескопированные клаттеры из тех, что стояли в очередь на копирование при входе в цикл.

2. Все то же самое, но как только новый клаттер из остатка собрать не получается, сеть копирует оставшиеся нескопированными клаттеры, заходит на следующий виток[18] и финализирует цикл. При этом некоторые клаттеры в данном цикле оказываются скопированными дважды.

3. Этот вариант среднее между первым и вторым. Копируются клаттеры, устанавливаются в сеть, число связей растет. Если новый клаттер, из оставшихся на копирование в последнем звене цикла собрать невозможно, но общее число неоткопированных позиций превосходит половину веса клаттера, то сеть заходит на новый виток. В противном случае – нет. Цикл на втором этапе может состоять из одного или двух витков.

4. Возможен также сценарий, при котором цикл самокопирования сети завершается в тот момент, когда из оставшихся на копирования клаттеров новый собрать невозможно, а следующий цикл начинается с нескопированных носителей этих клаттеров. Здесь, так же как в первом варианте финализации цикла, остаются нескопированные клаттеры из тех, что стояли в очередь на копирование при входе в цикл[21].

Все рассмотренные сценарии финализации звена на первом и втором этапе роста и цикла на втором дают для полного числа циклов (и числа циклов роста сети до ее гармонического размера) практически одинаковые результаты.

Рассмотрим в качестве примера рост сети 256 на втором этапе по четвертому сценарию финализации звена (с перехлестом) и по третьему сценарию финализации цикла. Пусть сеть 256, размер которой составляет 20 клаттеров, входит в цикл. Копирование идет с 13 клаттеров, составляющих одно звено: 13·20 = 260 > 256 (20-й клаттер скопирован не полностью, с него начнется следующее звено); собираем дочерний клаттер, устанавливаем в сеть, прокладываем связи; остается 7 нескопированных клаттеров (плюс нескопированные носители 20-го клаттера).

Т. к. 4+1+7·21 = 152 > 128 – копируем эти 7 клаттеров, заходим на второй виток, собираем и устанавливаем в сеть еще один клаттер. На этом цикл завершается. На втором витке в процесс копирования будут вовлечены клаттеры, уже скопированные в данном цикле. В следующем цикле клаттеры, скопированные в предыдущем цикле дважды, копируются так же, как клаттеры скопированные единожды.

Формально модель третьего этапа проста: создается копия совершенной финальной сети, прокладываются связи, запускается рост сети четвертого ранга. Попробуем тем не менее безо всякого ущерба для этого формализма создать наглядный образ (ни на что, впрочем, не претендующий) завершающего этапа роста сети и операции ее репликации.

Когда сеть 256 достигает совершенства ее размер (число клаттеров в сети) становится равным весу клаттера Р (числу носителей в клаттере). Рассмотренный здесь алгоритм роста не может больше работать, т. к. все носители каждого клаттера, связанные с его магистральным узлом[22], оказываются задействованными на поддержание внутрисетевых связей. Число связей клаттера совершенной сети не может быть увеличено, поэтому она и не может расти дальше.

Но, что такое связь? Можно создать наглядный образ связи, который следует понимать только как метафору. Будем считать, что связь от носителя каждого клаттера через магистральные узлы всех клаттеров более низкого ранга, в порядке иерархии составляющих сетеобразующий клаттер, идет к магистральному узлу этого клаттера, который соединяется через магистральный узел сети с носителями других клаттеров. При этом магистральные узлы клаттеров всех уровней и магистральный узел сети выступают в качестве «коммутаторов», обеспечивающих независимый обмен информацией между носителями.

Здесь предполагается, что каждый носитель может быть связан в данный момент времени только с каким-то одним носителем в своем или любом другом клаттере сети.

Переходим к операции репликации. В процессе роста сети третьего ранга длина звена, с которого собирается клаттер, уменьшалось от 128 до 2. На последнем цикле дочерний клаттер копировался с двух, а в его конце – практически с одного материнского.

Поэтому логично считать продолжением этого процесса операцию репликации (перехода), во время которой звено копирования минимально и равно единице, т. е. операцию, в процессе которой происходит точное копирование «клаттер в клаттер», с установкой копий носителей в новую в сеть.

Операцию репликации можно считать последней, предельной операцией копирования сети данного ранга. Чисто теоретически она может состоять из некоторого количества циклов, в процессе которых итоговая СИС и ее клоны самореплицируются до момента достижения некой стартовой конфигурации. Однако в дальнейшем всегда будем считать, что сеть, точно так же как живая клетка при делении, всегда создает только одну собственную копию.

Для обеспечения глобальной связности носителей СИС в процессе ее репликации сначала копируется магистральный узел полученной СИС четвертого ранга – он становится магистральным узлом второго клаттера растущей ИС четвертого ранга. Затем создается еще одна копия магистрального узла полученной СИС, которая кладется в основу магистрального узла растущей СИС четвертого ранга. Между этими тремя узлами прокладываются связи ИС четвертого ранга. Затем последовательно, клаттер за клаттером, создается копия итоговой совершенной ИС.

При этом в процессе операции репликации, так же как в процессе самокопирования ИС, каждый вновь поступающий носитель после установке его в сеть оказывается связанным с каждым носителем итоговой СИС и ее растущей копией.

Такая связность носителей ИС на всех стадиях ее роста обеспечивается тем, что сначала создается копия магистрального узла клаттера итоговой СИС и соединяется с магистральным узлом ее копии. Затем последовательно, в порядке иерархии копируются магистральные узлы клаттеров меньших рангов, и только после этого копируются носители и подключаются через их посредство к магистральному узлу клаттера-копии. При таком сценарии каждый вновь поступающий носитель оказывается сразу же подключенным ко всей сети.

По завершению операции репликации запускается рост сети четвертого ранга. При выборе алгоритма финализации звена на первом и втором этапе роста, и цикла на втором – важно, чтобы он обеспечивал прохождение всех гармонических стадий роста сети в момент завершения цикла, а не где-то у него внутри и, конечно же, этот алгоритм должен гарантировать достижение сетью в финале совершенства. Как показывает математическое моделирование предпочтение следует отдать третьему варианту, т. к. в этом случае на втором этапе гармонические стадии роста сети достигаются в моменты завершения циклов.

Кроме того, выясняется, что при заданном алгоритме и при всех прочих сценариях финализации звена и цикла гармонические стадии оказываются в этом смысле удивительно притягательными для растущей сети. При этом число циклов, которое проходит сеть, с рангом большим трех, от одной точки своего роста до другой практически не зависит ни от выбора правила финализации звена на первом и втором этапе роста, ни от правила финализации цикла — на втором.

И в заключение отметим следующее: в модели любого природного явления главное – математика (если, конечно, она там присутствует), а не ее интерпретация. Интерпретация процесса роста населения Земли в виде растущей ИС с узлами, связями, клаттерами, носителями – лишь один из вариантов интерпретации той математики, которая здесь представлена[23].

Рост сети 256

Рассмотрим рост сети 256 на первом этапе от 2-х клаттеров до 16-ти. Приведем пример программы подсчета числа клаттеров за цикл в зависимости от номера цикла, реализованной в системе MathCAD:

Рис. 1. Алгоритм роста сети 256 от 2-х клаттеров до 16-ти.

Здесь ceil(X) – ближайшее целое, большее или равное X; ce(X) – ближайшее целое, меньшее или равное X; cel(X) – ближайшее целое, меньшее X. Функция U(C) – это число клаттеров, собранных сетью за С циклов. Например, если U(133) = 7, то за 133 цикла собрано 7 клаттеров. C(2^k) – номера циклов, соответствующие гармоническим стадиям роста сети.

Всего получается 156 циклов. Из них пустых 156 − 14 = 142. Соответственно, за каждый из оставшихся 14 циклов собирается один клаттер (14 = 16 − 2). Заходить на второй виток ни разу не приходилось. Сеть проходит четыре гармонические стадии роста: в момент старта, а также на 93-м, 134-м и 156-м цикле с числом клаттеров 2, 4, 8 и 16, соответственно. Переходим ко второму этапу.

Рис. 2. Алгоритм роста сети 256 от 16-ти до 256-ти клаттеров.

На этом этапе пройдено 15 циклов. Его начало сопровождается бурным ростом числа клаттеров. Это связано с тем, что на втором этапе за цикл с нуля собирается один или большее число клаттеров. Для реализации прохода через гармонические сети необходимо было скорректировать рост, но только в четырех точках «близких» к гармоническим сетям.

Каждая коррекция представляла собой малое возмущение в один клаттер и была проведена на стадиях роста с числом клаттеров 20, 31, 65 и 127: (127 + 1)·2 = 256, (31 + 1)·8 = 256, (65-1)·4 = 256. Существует не одна такая четверка, но результат – функция U(C) – остается тем же.

Растущая сеть проходит через гармонические стадии с размером: 16, 32, 64, 128, 256 клаттеров. На последнем цикле число клаттеров удваивается: U(14) = 128, U(15) = 256. Это справедливо для сетей любого ранга. Отметим также, что результаты работы алгоритма практически полностью совпадают со значениями следующей функции:

Рис. 3. Теоретическая гипербола сети 256.

Назовем функцию U1(i) теоретической гиперболой сети 256. Этап заканчивается сборкой клаттера 65536. И, наконец, третий этап роста сети 256 – репликация. Здесь сеть собирает свою копию и прокладывает связь между ней и оригиналом. Получена стартовая конфигурация сети 65536.

Подведем итоги для сети 256: всего имеется 156 + 15 = 171 цикл (без учета репликации) и восемь гармонических стадий роста с числом клаттеров 2, 4, 8, 16, 32, 64, 128, 256. Последняя гармоническая сеть с числом клаттеров 256 является также совершенной.

Рост сети 65536

Продолжая процесс, переходим к сети 65536. Первый этап – рост от 2-х клаттеров до 256-ти.

Рис. 1. Рост сети 65536 от 2-х клаттеров до 256-ти.

Всего сеть проходит 42142 цикла. Из них пустых 42142 – 254 = 41888. В 254 циклах собиралось по одному клаттеру. На второй виток, в соответствии с алгоритмом, заходить не приходилось.

Имеется восемь гармонических стадий роста: на старте и на 23666-м, 33543-м, 38046-м, 40197-м, 41261-м, 41812-м, 42142-м циклах с числом 2, 4, 8, 16, 32, 64, 128 и 256 клаттеров, соответственно.

Второй этап – рост от 256-ти клаттеров до 65536-ти.

Рис. 2. Рост сети 65536 от 256-ти клаттеров до 65536-ти.

Коррекция роста проведена в 21 точке. Все значения размеров сети, для которых проводилась коррекция М <− М+1, являются (или «почти» являются) делителями числа 65536, если к ним добавить единицу; например, 65536/(13106+1) = 5,000076. Вот частные, которые получаются в результате:

3, 4, 5, 8, 19, 32, 56, 67, 94, 122, 212, 214, 217, 222, 225, 229, 234, 240.

Эти коррекции одни из многих возможных, подобных им, но все они дают практически один и тот же результат, если придерживаться правила: при небольшом отклонении от гиперболической сети добавить в цикл один клаттер, т. е. держать курс на ближайшую гиперболическую сеть. Гиперболическая сеть – это сеть, размер которой равен ce(65536/N), где N > 256 – натуральное число.

Причем при увеличении М на единицу процесс устойчив и через некоторое количество циклов «садится» на гиперболу. При уменьшении М на единицу наблюдается неустойчивость, и процесс роста необратимо уходит от гармонических сетей.

Понадобилась одна коррекция в сторону уменьшения размера сети М: 328 <− 327 (65536/328 = 199.8), если ее не провести процесс срывается с гиперболы (последние три цикла 25501, 43735, 65537). Результаты работы алгоритма «почти точно» ложатся на теоретическую гиперболу сети 65536:

Рис. 3. Теоретическая гипербола сети 65536.

Гиперболический рост сети на первом и втором этапе представляет собой ускоряющийся неустойчивый процесс, требующий от управляющей системы двадцать пять коррекций. Неустойчивость роста понятна и из того факта, что уравнение Капицы, как асимптотический закон роста сети, устойчивых решений не имеет.

Составим таблицу зависимости числа клаттеров растущей сети от номера цикла для алгоритма и теоретической гиперболы. Зависимости почти не отличаются: максимальное отличие в три клаттера. В таблице выделены гармонические размеры сети.

Таблица 1. Зависимость числа клаттеров растущей сети от номера цикла для алгоритма и теоретической гиперболы.

Третий этап – операция репликации. Собираются копия сети, прокладывается связь между ней и оригиналом. Сеть 4 294 967 296 может стартовать.

Всего имеется 42142 + 255 = 42397 циклов (без учета репликации) и 16 гармонических стадий роста сети 65536. Сведем все данные в таблицы:

Таблица 2А. Подсчет номера цикла C_j и числа клаттеров M_j для гармонических сетей с размером, принадлежащем интервалу [257, 65536].

Таблица 2В. Зависимость числа клаттеров от номера цикла для гармонических размеров сети 65536.

Подсчет числа циклов роста сети любого ранга от двух клаттеров до совершенной

Для того, чтобы найти полное количество циклов, которое в процессе своей эволюции проходит сеть любого ранга, нужно сложить число этих циклов на трех этапах ее роста (считаем, что сеть любого ранга, став совершенной, создает единственную свою копию, на что уходит ровно два цикла[24], и рост сети следующего ранга всегда начинается с двух клаттеров).

На втором и третьем этапе число циклов вычисляется с полной определенностью: корень квадратный из веса клаттера минус единица плюс два. Минус единица, т. к. алгоритм восьми шагов прекращает свою работу за шаг до сингулярности. И далее два цикла на переход. Получаем корень квадратный из веса клаттера плюс единица.

Но наибольший вклад в количество циклов, пройденных сетью за все время ее роста, дает первый этап. Причем для сетей с рангом большим трех число циклов на втором этапе гораздо меньше, чем на первом и им, с небольшой потерей в точности, можно пренебречь. Следовательно, наиболее важным представляется подсчет числа циклов на первом этапе. Еще раз проведем такой подсчет, но уже для сети любого ранга.

Здесь, как мы уже отмечали ранее, нас подстерегает неоднозначность[32]. Действительно, в приложении этой математики к процессу роста населения Земли время эволюции Сети человека на всех этапах ее роста должно исчисляться целым числом циклов. Поскольку на первом этапе копирование происходит звеньями, проблема возникает с последним циклом звена, если вес клаттера не делится нацело на квадрат размера сети. Рассмотрим, к примеру, рост сети четвертого ранга от трех клаттеров до четырех. Для сборки четвертого клаттера потребуется 65536/3² = 7281 целых, плюс 7/9 цикла. Т. к. 7:3 = 2·3+1, четвертый клаттер будет собран после копирования первой позиции последнего из стоящих в очередь на копирование клаттера 7282-го цикла.

Т. к. звено замыкается здесь не в в момент завершения цикла, а у него внутри, то непонятно как округлять частное от деления веса клаттера на число носителей, которое копируется за цикл: с избытком, с недостатком или вообще не округлять? Возможны четыре варианта финализации звена на первом этапе:

1) Отдаем остаток последнему полному циклу или распределяем его по каким-то из предыдущих, при этом на некоторых из них будет скопировано число носителей больше планового (звено состоит из 7281 цикла в нашем примере).

2) Добавляем еще один цикл и переносим в него остаток (7 – в нашем примере) плюс некоторое число позиций, которые не будем копировать в текущем цикле (2 – в нашем примере); при этом носителей на последнем цикле будет скопировано меньше планового (звено состоит из 7282 циклов в нашем примере).

3) Этот вариант среднее между первым и вторым: если остаток меньше или равен половине квадрата размера сети идем по первому варианту, в противном случае – по второму (7281 или 7282 цикла в звене в нашем примере; т. к. 7 > 3²/2, берем 7282).

4) Есть еще один сценарий финализации звена, а именно: с перехлестом (без округления), когда следующее звено начинается внутри последнего цикла предыдущего звена с копирования его нескопированных носителей. Последний цикл текущего звена будет завершен здесь в начале следующего звена. В нашем примере сразу после копировании первой позиции последнего клаттера 7282-го цикла собираем четвертый клаттер и подключаем его к остальным. Начинаем следующее звено с копирования трех (2+1) позиций третьего клаттера и только тогда завершаем 7282-й цикл. Новоиспеченный четвертый клаттер в 7282-м цикле не копируем, а сразу начинаем новый цикл. Заметим, что последний цикл звена в этом случае не является (в любом из вариантов) формально циклом по определению, поскольку число скопированных позиций здесь либо больше, либо меньше квадрата размера сети.

Третий и четвертый вариант рассматривать не будем, т. к. результаты вычислений здесь практически не отличаются от результатов по первому и второму. На рис. 1 представлены формулы для подсчета полного числа циклов роста сети любого ранга по первому и второму варианту работы с остатком, а также приближенная формула. Отрицательная добавка к сумме в виде логарифма от корня при подсчете по второму варианту учитывает то, что при делении К_n на степень двойки результат получается целым, без остатка, но лишняя единица (цикл) все равно добавляется.

Рис. 1. Подсчет числа циклов роста сети ранга «n» от двух клаттеров до совершенной плюс два цикла (характерного времени) на переход.

Составим таблицу зависимости количества циклов роста сети от ее ранга (n = 0, 1…7).

Таблица 1. Число циклов роста ИС от двух клаттеров ранга «n» до двух клаттеров ранга «n+1» по первому и второму варианту, а также по приближенной формуле.

Число циклов каждого следующего этапа можно оценить, если число циклов предыдущего возвести в квадрат и результат умножить на 1,55. Для сетей с рангом n > 5 результаты подсчета по трем вариантам c точностью до семи значащих цифр – не отличаются. При подсчете полного числа циклов роста сетей четвертого и пятого ранга, которые рассматриваются в этой книге, выбираем второй вариант работы с остатком. (Если выбрать первый – на результат это практически не повлияет.)

Выводы по растущим иерархическим сетям

Клаттер – это структурная единица растущей ИС (иерархической сети); представляет собой СИС (совершенную ИС) на единицу меньшего ранга, чем ранг собираемой СИС.

Носитель (клаттер-носитель, узел сети ранга нуль) представляет самый нижний уровень сетевой иерархии. Это бесструктурный сетеобразующий клаттер сети ранга нуль – сети, образованной двумя носителями, соединенными одной связью. Носитель не имеет в данной упрощенной модели своего ранга. (В приложении этой модели к мировой демографии будет пониматься как единое целое с человеком, к нему прикрепленным.)

Вес клаттера P – это число носителей, которое он содержит.

Размер сети L – это число клаттеров, которое она содержит.

Магистральный узел клаттера/совершенной сети – это магистральный узел, к которому сходятся связи от узлов клаттеров на единицу меньшего ранга, образующих данный клаттер. Узел носителя, изображаемого точкой в гра́фе СИС, совпадает с этой точкой.

Магистральный узел растущей сети – это коммутатор, к которому проложены связи от каждого из магистральных узлов сетеобразующих клаттеров. Позволяет устанавливать соединение между любой парой клаттеров сети.

Связи сети. Каждую связь, соединяющую любые два клаттера сети, считаем проходящей через магистральный узел клаттера и магистральный узел растущей сети, с которым в приложении данной математической модели к мировому демографическому процессу связана ее «индивидуальность». И каждую такую связь можно рассматривать как гиперсвязь, состоящую из Р связей, позволяющих соединять любые пары носителей растущей ИС, в каком бы клаттере они ни находились. Связь самого нижнего уровня подключается к носителю, причем носитель может поддерживать только одну такую связь.

Рост ИС любого ранга всегда начинается с двух клаттеров и представляет собой процесс самокопирования сети, которое происходит последовательно (клаттер за клаттером) по схематическому правилу: один носитель с узла и по одному носителю с каждой связи, входящей в копируемый клаттер. Или по другому: на каждом клаттере копируется число носителей, равное текущему размеру сети[33].

Ранг R такой растущей ИС считается равным рангу сетеобразующего клаттера (при R ≥ 2). Число связей, которыми каждый клаттер может быть соединен с другими, не превышает его веса Р, т. е. числа носителей, в нем содержащихся.

Цикл – это такой этап роста ИС, на котором в произвольном порядке и без повторения копируются все клаттеры (плюс-минус…), из имеющихся в ИС к моменту входа в этот цикл.

Звено – это последовательность материнских клаттеров, в процессе копирования которых полностью собирается очередной дочерний клаттер.

Длина звена Z – это число клаттеров, входящих в звено; за время роста сети Z уменьшается от половины веса клаттера (Р/2) до единицы. На первом этапе роста сети (√P < Z ≤ P/2) звено состоит из циклов, на втором этапе (1 < Z ≤ √P) – цикл состоит из звеньев. Собранный клаттер устанавливается в ИС, т. е. его магистральный узел соединяется с магистральным узлом растущей сети и ее размер увеличивается на единицу. В очередь на копирование в текущем цикле такой новоиспеченный клаттер уже не ставится. (Чего не скажешь о связях, исходящих из него и входящих через магистральный узел растущей сети в другие клаттеры. Подключение этих связей в процессе цикла на втором этапе придает росту сети дополнительное ускорение.)

Если в процессе цикла на первом этапе роста не удается собрать ни одного клаттера (с учетом носителей, собранных на всех предыдущих циклах звена), то такой цикл называется пустым и заканчивается последним клаттером, из имеющихся в сети в момент входа в цикл (за исключением, возможно, последнего цикла звена). Все носители, скопированные в процессе пустого цикла идут на сборку нового клаттера. Правило финализации звена на первом этапе выбираем следующим:

Если число циклов звена не является целым и его дробная часть больше или равна ½, то это число возрастает на единицу; если меньше – число циклов округляется до целого отбрасыванием дробной части, а избыточные носители отдаются последнему клаттеру звена или распределяются по каким-то из предыдущих. (Возможен также сценарий, при котором звено копирования замыкается не в момент завершения цикла, а где-то у него внутри. После установки клаттера в сеть и прокладки дополнительных связей следующее звено, завершающее цикл, начинается с нескопированных носителей предыдущего, плюс один носитель.)

Каждое следующее звено на втором этапе роста начинается с копирования нескопированных носителей последнего клаттера предыдущего звена (сценарий с «перехлестом»). Если суммы носителей последнего звена цикла на втором этапе недостаточно для сборки нового клаттера, но эта сумма больше/равна половины/е веса клаттера, то цикл продолжается: процесс копирования заходит на второй виток и копируются клаттеры, уже скопированные в данном цикле.

Если эта сумма оказывается меньше половины веса клаттера происходит финализация цикла. При этом некоторые клаттеры, из имеющихся в сети в момент входа в цикл, оказываются нескопированными или скопированными не полностью.

На втором этапе роста производится коррекция выхода клаттеров с некоторых циклов (плюс – минус один) в направлении на ближайшую гиперболическую сеть.

Рост сети, описываемый данным алгоритмом, процесс неустойчивый и малейшее возмущение быстро уводит его от теоретической гиперболы (тут еще нужно учесть то, что здесь мы имеем дело с целочисленными величинами). Что совершенно неудивительно, т. к. и закон квадратичного роста (уравнение Капицы), являющийся асимптотическим приближением алгоритма, – устойчивых решений не имеет, т. е. обладает точно таким же свойством.

Эта коррекция представляет собой небольшое число очень малых возмущений, всего в один клаттер, тогда как сеть на втором этапе своего роста, который здесь только и рассматривается, растет от 256 клаттеров до 65536, т. е. ее размер составляет сотни, тысячи и даже десятки тысяч клаттеров. В таком случае возмущение в один клаттер составляет всего лишь доли процента от общего числа клаттеров в сети и является даже не каким-то «толчком», а всего лишь «легким прикосновением».

Существует множество вариантов коррекции выхода клаттеров на втором этапе, каждый из которых приводит ИС к совершенной через гармонические сети. Все они дают практически одну и ту же зависимость числа клаттеров растущей сети от номера цикла.

И, наконец, полученная СИС проходит еще один цикл[34] – операцию репликации, во время которой длина звена копирования минимальна и равна единице (Z = 1). В ее начале создается магистральный узел будущей копии СИС, магистральный узел сети следующего ранга и прокладываются гиперсвязи, соединяющие их с магистральным узлом сети-оригинала. В процессе этой операции происходит копирование сети-оригинала в сеть-копию по правилу «клаттер в клаттер» с установкой копий клаттеров в новую сеть. Это последняя, предельная операция копирования сети данного ранга. По ее завершению запускается рост сети на единицу большего ранга.