Глава I
Общие закономерности процессов переноса
В реальных условиях процессы переноса импульса, тепла и массы протекают как в сплошной среде (гомогенной), так и в гетерогенной системе, при наличии двух и более фаз. В случае сушки, при наличии твердой фазы процесс протекает в системе газ – твердое тело. Стационарные процессы различных видов переноса в сплошной среде изучены достаточно хорошо [1, 6, 9]. Процессы же переноса импульса, тепла и массы, протекающие в гетерогенной системе, как правило, не стационарны. Они менее изучены, т. к. нестационарность значительно усложняет описание кинетики этих процессов.
Хотя в реальных условиях возможно одновременное протекание различных видов переноса, иногда осложненное еще и химической реакцией, для изучения закономерностей переноса протекающие в промышленности процессы переноса рассматривают отдельно и классифицируют их следующим образом.
Механические – процессы механической обработки твердых материалов (основываются на законах механики твердого тела). Это процессы резания, деформации, дробления, смешения, сепарации и т. д.
Гидромеханические – процессы, описывающие движение жидкостей, газов (паров) как однофазных систем, так и многофазных, в т. ч. с взвешенными твердыми частицами. Они основываются на законах гидрогазодинамики (перенос импульса). Эти процессы описывают течения в трубах, аппаратах, каналах, насосах, компрессорах т. д.
Тепловые – процессы разного вида распространения тепла в гомогенных и гетерогенных системах, основаны на законах теплопроводности, теплообмена (перенос тепла). Эти процессы нагрева, охлаждения, конденсации, испарения т. д.
Массообменные – процессы переноса вещества в гомогенных и гетерогенных системах, основываются на законах диффузии, массообмена. Наиболее часто массообмен протекает между двумя фазами, через межфазную поверхность. Эти процессы пропитки, крашения, растворения, кристаллизации, экстракции т. д.
Химические – процессы получения новых веществ на основе протекающих химических реакций, описываются законами химической кинетики. Эти процессы получения аммиака, каучука, различных кислот, щелочей, солей, горения топлив т. д.
На практике процессы часто являются совмещенными. Так при сушке удаление влаги (массообмен) происходит обычно при нагревании материала и, следовательно, процесс тепломассооменный (перенос тепла и массы).
1.1 Закон сохранения массы
Одним из главных законов при переносе массы является закон сохранения массы. Этот закон установлен М. В. Ломоносовым. Для элементарного объема он может быть получен следующим образом.
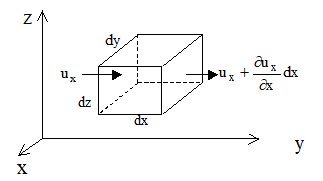
Рис. 1.1 К выводу закона сохранения массы.
Рассмотрим поток вещества через грани элементарного объема. Плотность ρ и скорость потока u в общем случае изменяются в пространстве и во времени:

Рассмотрим изменение массы вдоль оси х (Рис. 1.1). Если проекция скорости потока на входе в элементарный объем ux, то на выходе из него, с учетом изменения на длине dx она составит:

.
Тогда изменение массы вдоль оси х за счет изменения скорости составит:

.
Аналогично определяется изменение массы вдоль остальных осей. Суммарное изменение массы, отнесенное к единице объема, вдоль всех координат должно быть равно нулю:

Выражение в скобках в уравнении (1.2) называется дивергенцией вектора скорости и обозначается div u. С учетом его получим для (1.2):

Это выражение закона сохранения массы и оно известно в гидродинамике, как уравнение сплошности, неразрывности потока. В элементарной форме это уравнение для одномерного потока, движущегося со средней скоростью v примет вид:

где М – массовый расход потока, S – площадь его поперечного сечения.
Для несжимаемых жидкостей (ρ = Const) уравнение (1.3) упрощается:

Для описания химического процесса в уравнении (1.2) вместо плотности подставляют массовую концентрацию компонента С. С учетом скорости образования этого компонента по химической реакции r, если она имеет место, для уравнения (1.2) получим:

С учетом, что концентрация компонента изменяется в пространстве и во времени, получим:

В частном случае для стационарных процессов первый член в левой части уравнения (1.6) равен нулю, а в случае отсутствия химической реакции правый член этого уравнения также равен нулю.
1.2 Закон сохранения количества движения
В движущемся потоке газа или жидкости действуют массовые и поверхностные силы. Они оказывают влияние на взаимодействие, соударения молекул, что обуславливает перенос количества движения. По второму закону Ньютона изменение количества движения в единицу времени (импульс) численно равно силе:

Поэтому баланс сил в движущемся потоке представляет собой закон сохранения количества движения (импульса).

Рис. 1.2 К выводу закона сохранения количества движения.
Рассмотрим равновесие сил в движущемся потоке в проекциях на ось х (Рис. 1.2). На правую и левую грани действуют силы давления. Их проекция на ось х составит –

.
Проекция массовой силы Q на ось х запишется:

.
На верхнюю и нижнюю грани действуют силы вязкостного трения. Их проекция на ось х составит  .
.
С учетом закона Ньютона для вязкостного трения:

имеем проекцию сил вязкостного трения на ось х:

.
Здесь выражение в скобках – оператор Лапласа от проекции скорости на ось х, он обозначается Δux или 2ux.
Так как сумма проекций всех сил равна проекции силы инерции:

,
относя все силы к единице объема, получим:

Последние два уравнения получены аналогично для осей у и z, а в целом система уравнений (1.10) в гидрогазодинамике называется уравнениями движения вязкой жидкости Навье-Стокса и выражает закон сохранения количества движения.
Система уравнений Навье-Стокса может быть записана более детально, если раскрыть полную производную проекции скорости. Так уравнение для оси х, например, при делении всех его членов на ρ , c учетом, что ν = μ/ρ, будет иметь вид:

.
Аналогично записываются уравнения для осей у и z.
1.3 Закон сохранения энергии
Рассмотрим сначала закон сохранения энергии для движения идеальной жидкости. Так как в идеальной жидкости отсутствуют силы вязкостного трения, то для этого случая из системы уравнений (1.10), положив проекции силы вязкости равным нулю, получим следующую систему (система уравнений движения идеальной жидкости Эйлера):

.
Помножим эти уравнения соответственно на dx, dy, dz и сложим. Тогда, преобразуя, получим следующее уравнение:

В поле силы тяжести (Х = 0; У = 0; Z = – g) уравнение (1.12) примет вид:

Это уравнение определяет в дифференциальном виде закон сохранения энергии для движения идеальной жидкости и представляет собой, соответственно, сумму удельных (отнесенных к единице массы) потенциальных энергий положения и давления и кинетической энергии. При интегрировании уравнения (1.13) для потока несжимаемой жидкости (ρ = Const) получим уравнение Бернулли для одномерного потока, движущегося со средней скоростью v:

Уравнение Бернулли показывает, что для идеальной жидкости сумма потенциальной и кинетической энергий остается постоянной вдоль всего потока.
В более общей форме закон сохранения энергии описывает 1-й закон термодинамики: теплота, подводимая к системе, идет на производство работы и увеличение энергии системы:

Выражение для потока энергии в дифференциальном виде включает ее члены, входящие в уравнение (1.13) плюс, внутренняя энергия dU. С учетом этого запишем уравнение (1.15) в следующем виде:

Сумма второго и третьего членов правой части уравнения (1.16) представляет собой изменение энтальпии dh. С учетом этого получим другой вид уравнения (1.16):

1.4 Микро- и макроперенос
Молекулярный перенос, называемый еще микропереносом, происходит вследствие беспорядочного теплового движения микрочастиц (броуновское движение), когда среда в целом неподвижна. Перенос массы при наличии молекулярного переноса называется молекулярной диффузией. Перенос тепла под действием молекулярного переноса называется теплопроводностью. Перенос количества движения под действием молекулярного переноса происходит при наличии молекулярного (вязкостного) трения при ламинарном движении среды. Процесс микропереноса описывается микрокинетикой.
Примером микропереноса массы может служить диффузия капли красителя, чернил в сосуде с водой, происходящая вследствие теплового движения молекул воды. В процессе переноса массы в сосуде создаются поля концентрации красителя. Эти поля изменяются во времени (микрокинетика) до момента равномерного распределения концентрации красителя по всему объему. Процесс в зависимости от свойств и параметров (объем, температура) системы может занять от долей секунды до нескольких часов и даже суток. Движущей силой переноса в этом случае является разность концентраций красителя в разных точках объема. Поля концентраций в этом случае не стационарны. Достижение момента равномерного распределения концентрации красителя соответствует состоянию материального равновесия (постоянства состава по объему).
В качестве примера микропереноса тепла можно рассмотреть процесс теплопереноса при погружении нагретого шара в сосуд с жидкостью. Микроперенос обеспечивается теплопроводностью жидкости и шара. Поле температур изменяется во времени до момента установления равенства температур в погруженном теле и в жидкости. Движущей силой переноса в этом случае является разность температур в разных точках объема. Поле температур как в теле, так и в жидкости не стационарно. Достижение момента равномерного распределения температур соответствует состоянию теплового равновесия (постоянства температуры во всем объеме).
Примером микропереноса количества движения, происходящего вследствие наличия молекулярного (вязкостного) трения при ламинарном движении среды может служить осаждение малых частиц в жидкости. При осаждении скорость частицы возрастает от нуля до конечного значения, обусловленного равновесием сил, действующих на частицу – тяжести, архимедовой и сопротивления среды. Движение частицы в этом случае описывается законом Стокса. Движущей силой переноса в этом случае является разность скоростей. Движение частицы в начальный период не стационарно. При достижении постоянной скорости осаждения (сила инерции частицы равна нулю) достигается постоянство распределения скоростей (эпюры скоростей) при осаждении частицы. Движение частицы становится стационарным.
Макроперенос – это перенос определенных объемов массы, перенос энергии этих объемов, перенос количества движения, которым обладают эти объемы. Макроперенос обусловлен наличием конвекции (свободной или вынужденной), вихреобразованиями. Кинетика процесса макропереноса называется макрокинетикой.
Рассмотренные выше примеры микропереноса могут быть реализованы в условиях макропереноса. Так для ускорения диффузии красителя в сосуде с водой необходимо использовать перемешивание. Возникающие при этом циркуляционные токи значительно быстрее, чем при микропереносе, выровняют концентрацию красителя по всему объему.
В примере с теплопереносом от нагретого шара к жидкости, для интенсификации процесса также достаточно применить перемешивание. Конвективный макроперенос тепла протекает значительно быстрее, чем перенос теплопроводностью.
Макроперенос количества движения происходит, например, при осаждении крупных частиц в турбулентном режиме за счет образования турбулентных завихрений. Движение частицы в этом случае описывается законом Ньютона.
При макропереносе имеет место также и микроперенос, однако интенсивность последнего намного ниже. При движении среды макроперенос, как правило, превалирует по сравнению с микропереносом. Именно поэтому макрокинетика наиболее важна, как определяющая все виды процессов переноса – переноса массы, энергии и количества движения или импульса.
1.5 Перенос массы
Рассмотрим поток вещества J в пространстве (Рис. 1.3). Концентрация вещества С изменяется в пространстве и во времени т. е.  .
.
Вектор потока вещества между двумя изотермическими поверхностями, расположенными на бесконечно малом расстоянии dn друг от друга перпендикулярен к поверхности в любой точке [6].

Рис. 1.3 Поток вещества в пространстве.
Поток вещества J, отнесенный к единице поверхности S в этом случае будет пропорционален градиенту концентрации:

Это выражение называется 1-м законом Фика. Здесь D – коэффициент диффузии.
Закон молекулярного переноса массы (вещества) для элементарного объема может быть получен следующим образом. Рассмотрим поток вещества через грани элементарного объема.
Расход вещества, обусловленный диффузией вдоль оси х через левую поверхность dy·dz (Рис. 1.4), с учетом закона Фика, составит.

На расстоянии dx, с учетом изменения концентрации, получим ее значение

.
Тогда расход вещества, обусловленный диффузией вдоль оси х через правую грань dy·dz, составит 
Таким образом, за счет изменения концентрации вдоль оси х в элементарный объем поступит количество вещества.


Рис. 1.4 К выводу 2-го закона Фика.
Аналогично определяется изменение количество вещества вдоль остальных осей. Суммарное изменение количество вещества, в пересчете на единицу объема, вдоль всех координат должно быть равно изменению его концентрации во времени:

Выражение в скобках в уравнении (1.19) является оператором Лапласа. С учетом его сокращенного обозначения и образования вещества за счет химической реакции при скорости образования r получим для выражения (1.19):

Уравнение (1.20) является следствием закона сохранения массы и 1-го закона Фика и называется 2-м законом Фика. Оно определяет поле концентраций для молекулярной диффузии в рассматриваемой среде.
Для изотропной диффузии уравнение (1.20) может быть записано для изменения вдоль любой оси, например х, в следующем виде:

При переносе массы в движущейся среде имеет место конвективный перенос и перенос за счет молекулярной диффузии. Тогда вместо частной производной концентрации по времени в уравнении (1.20) надо писать полную производную, учитывающую и конвективный перенос. С учетом этого для (1.20) получим:

Уравнение (1.22) определяет поле концентраций с учетом молекулярной и конвективной диффузии. Как следует из этого уравнения, для описания макрокинетики процесса переноса массы необходимо учитывать гидродинамику и поэтому уравнение переноса в движущейся среде (1.22) должно быть дополнено уравнениями движения Навье-Стокса (1.10), определяющими поле скоростей и перенос импульса в движущейся среде.
Необходимо также отметить, что приведенные в данном разделе уравнения применимы для изотермической конвективной и молекулярной диффузии. Влияние изменения температуры описывается при молекулярном и конвективном переносе тепла.
1.6 Перенос тепла
Рассмотрим молекулярный перенос тепла аналогично переносу массы (Рис. 1.3). Температура t в общем случае изменяется как в пространстве, так и во времени т. е.  .
.
Тогда поток тепла q, отнесенный к единице поверхности S будет пропорционален градиенту температуры в произвольном направлении n:

Это выражение называется законом теплопроводности Фурье. Здесь – коэффициент теплопроводности среды.
Закон молекулярного переноса теплоты для элементарного объема может быть получен аналогичным образом, как и для переноса массы. Тогда суммарное изменение количества тепла вдоль всех 3-х координат элементарного объема, проявляющееся в изменении температуры, равно изменению температуры, вовремя помноженному на произведение теплоемкости ср на плотность ρ [6]:

Выражение в скобках в уравнении (1.24) является оператором Лапласа, с учетом его сокращенного обозначения и дополнительного источника тепла qr, например, за счет химической реакции, с введением коэффициента температуропроводности а = / ср ρ, получим для выражения (1.24):

Уравнение (1.25) является следствием закона Фурье и также называется его именем. Оно определяет поле температур для молекулярного переноса тепла в рассматриваемой среде.
Для одномерной теплопроводности, например, вдоль оси х, уравнение (1.25) может быть записано в следующем виде:
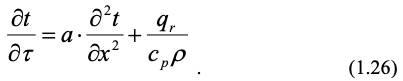
При переносе тепла в движущейся среде имеет место конвективный перенос и перенос за счет молекулярной диффузии. Тогда вместо частной производной температуры по времени в уравнении (1.25) надо писать полную производную, учитывающую и конвективный перенос. С учетом этого для (1.25) получим

Уравнение (1.27) называется уравнением Фурье-Кирхгофа и определяет поле температур с учетом молекулярного и конвективного переноса тепла. Как следует из этого уравнения, для описания макрокинетики процесса теплопереноса необходимо учитывать гидродинамику и уравнение переноса в движущейся среде (1.27) должно быть дополнено уравнениями движения Навье-Стокса (1.10), определяющими поле скоростей в движущейся среде.
1.7 Перенос количества движения
По второму закону Ньютона изменение количества движения в единицу времени (импульс) численно равно силе – уравнение (1.8). В движущемся потоке газа или жидкости под действием массовых и поверхностных сил происходят соударения молекул, что обуславливает перенос количества движения. Баланс сил в движущемся потоке представляет собой закон сохранения количества движения (импульса). На основе баланса сил получена выше система уравнений Навье-Стокса (1.10).
Строго говоря, т. к. система уравнений Навье-Стокса получена на основе закона Ньютона для вязкостного трения (1.9), учитывающего молекулярный перенос количества движения (микроперенос), она применима только для струйчатого, ламинарного движения вязкой жидкости.
Если жидкости отклоняются от закона Ньютона, то их называют неньютоновскими. К ним относятся жидкие полимеры, растворы высокомолекулярных полимеров, суспензии и др.
Макроперенос количества движения обусловлен конвективными токами, турбулентными образованьями, вихрями. Если микроперенос осуществляется только за счет теплового движения молекул, то макроперенос обусловлен не только молекулярным механизмом, но главным образом за счет более быстрого переноса макроколичеств среды. В результате этого в жидкости возникает дополнительное трение. Оно учитывается коэффициентом турбулентной вязкости т. Тогда формула (1.9) примет вид:

Можно показать [6], что в этом случае система уравнений Навье-Стокса формально останется той же (1.10), но вместо ньютоновской вязкости μ необходимо подставить в нее сумму ньютоновской и турбулентной вязкости μт.
Поле скоростей при микропереносе количества движения определяется при решении системы уравнений Навье-Стокса (1.10), а при макропереносе количества движения определяется из решения системы уравнений Навье-Стокса с учетом турбулентной вязкости. Следует отметить, что если ньютоновская вязкость является величиной постоянной для данной среды, то турбулентная вязкость зависит от масштаба турбулентности и поэтому при ее расчете, возникают определенные трудности.
1.8 Аналогия процессов переноса
Сравнивая выражения для трех видов молекулярного переноса массы (1.18) – закон Фика, переноса тепла (1.23) – закон Фурье и переноса количества движения (1.9) – закон Ньютона, нетрудно заметить, что по форме они абсолютно аналогичны.

.
Здесь эти уравнения дополнены еще одним видом переноса – переносом электричества. Где u – градиент напряжения или электрический потенциал, ρ – удельное сопротивление электрического тока.
Имеется очевидное подобие выражений для конвективного переноса массы (1.22), переноса тепла (1.27) – закон Фурье и переноса количества движения (1.10), записанных ниже для одномерного потока:

Приведенные уравнения тождественны по форме. Их левые части представляют собой, соответственно, скорость переноса массы, теплоты и количества движения в пространстве. Первые члены правой части представляют собой, соответственно, скорость молекулярного переноса массы, теплоты и количества движения, а вторые – характеризуют интенсивность внешнего источника. Одинаковая форма уравнений, описывающих разные виды переноса, указывает на подобие полей концентраций, температур и скоростей в рассматриваемых процессах.
На аналогию трех видов переноса указывает и одинаковая размерность коэффициентов переноса а, D и ν равная [м2/с]. Для газов механизм молекулярного переноса одинаков для переноса массы, теплоты и количества движения, т. к. связан с тепловым движением молекул. Поэтому все три коэффициента имеют один порядок с произведением длины свободного пробега молекул L на скорость их теплового движения u*:

.
Для жидкостей соотношение этих коэффициентов следующее:
ν а D.
При турбулентном движении газа и жидкостей роль всех трех коэффициентов может играть коэффициент турбулентного обмена [10], равный для изотропной турбулентности произведению масштаба турбулентности l на среднюю пульсационную скорость u.
Подобие различных видов переноса позволяет использовать общий математический аппарат, общие методы решения уравнений, описывающих перенос. Для моделирования различных процессов переноса можно использовать метод электродинамической аналогии на аналоговых ЭВМ (подобие переносу электричества) или подобие другого вида переноса. Так, передаче тепла теплопроводностью соответствует молекулярный массоперенос, а передаче тепла конвекцией – конвективный массоперенос. Только передача тепла излучением (передача энергии в форме электромагнитных волн в инфракрасном спектре) не имеет аналогии в массопереносе.
Вследствие подобия теоретические и экспериментальные результаты исследования, например, процессов теплопереноса могут быть непосредственно применены к процессам диффузии и наоборот [10]. В то же время экспериментальное изучение теплопереноса проводится в среде с переменной температурой. При этом на результатах исследования сказывается зависимость физических констант от температуры и приходится использовать усредненные по температуре значения этих констант, что вносит погрешности в расчеты. По этой причине можно рекомендовать для получения более точных зависимостей для конвективного теплопереноса использовать метод аналогии с массопереносом. По этой же причине в данной монографии наибольшее внимание уделено массопереносу, а вопросы теплопереноса рассмотрены как вторичные.
1.9 Экспериментальный подход к исследованию процессов переноса
Как следует из вышеизложенного, расчеты процессов микро- и макропереноса достаточно сложны, т. к. необходимо решать систему уравнений в частных производных, причем расчеты конвективного переноса массы, теплоты и количества движения значительно сложнее молекулярного переноса. Решение такой системы уравнений возможно в ряде частных случаев, а в общем случае возможно только численными методами и поэтому прибегают к использованию эмпирических зависимостей.
Так для расчета процессов теплопереноса используют эмпирический коэффициент теплоотдачи , равный отношению потока тепла q к разности температур Δt. Тогда тепловой поток равен:

Распределение температур от одной среды к другой в стационарной теплопередаче (постоянство во времени потока тепла q) через стенку толщиной δ с коэффициентом теплопроводности приведено на Рис. 1.5.
Применяя уравнение (1.29) для 1-й и 2-й среды, с учетом теплопроводности через стенку толщиной δ и общего коэффициента теплопередачи К, получим равенство выражений для стационарного теплового потока:
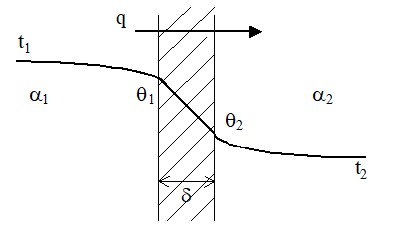
Рис. 1.5. Распределение температур при теплопередаче через стенку.

С учетом этих соотношений получим уравнение:

Физический смысл соотношения (1.31) заключается в том, что общее сопротивление теплопередачи через стенку 1/К равно сумме сопротивления переноса тепла от 1-й среды к стенке 1/α1, термосопротивления стенки δ/ и сопротивления переноса тепла от стенки ко 2-й среде 1/α2.
Аналогично для расчета процессов массопереноса используют эмпирические коэффициенты массопереноса К и массоотдачи .
Распределение концентраций вещества в стационарной массопередаче через поверхность раздела фаз от одной среды (газовая) к другой (жидкая) приведено на Рис. 1.6.
Коэффициенты массоотдачи для обеих сред могут быть найдены из выражения диффузионного потока, как выражения потока массы М на единицу поверхности:

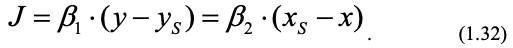
Значения концентраций на границе xs и уs трудноопределимы, поэтому записывают другое выражение диффузионного потока для коэффициентов массопереноса для первой среды К1 и для второй К2 через соответственно равновесные концентрации x* и y*.

Рис. 1.6. Распределение концентраций при массопередаче через поверхность раздела фаз.

Обычно принимают линейный закон (m – константа равновесия, тангенс угла наклона линии равновесия) для определения равновесных концентраций на границе [6]:

Из очевидного равенства:

находим с учетом (1.32) и (1.33):

К1 – коэффициент массопереноса по газовой фазе.
Физический смысл соотношения (1.36) заключается в том, что общее сопротивление процесса массопередачи через межфазную поверхность 1/К1 равно сумме сопротивления переноса вещества от 1-й среды к межфазной поверхности 1/1 и сопротивления переноса вещества от межфазной поверхности ко 2-й среде m/2.
Аналогично можно получить закон сложения сопротивлений для коэффициента массопереноса по жидкой фазе:

Сложность расчета по уравнениям (1.33) – (1.36), особенно в системах с подвижной поверхностью раздела фаз, заключается в том, что часто точно неизвестна ни поверхность раздела фаз, ни значения концентраций на ней, ни коэффициенты массопереноса.
Эмпирические коэффициенты тепло- и массоотдачи определяют на основании экспериментов, обработка которых проводится в виде критериальных зависимостей (зависимости между безразмерными параметрами), полученных на основании теории подобия.
1.10 Основы теории подобия
Экспериментальные исследования более удобно и экономически выгоднее проводить не на больших объектах, а на их моделях. Затем с помощью теории подобия можно распространить полученные на моделях опытные закономерности на подобные объекты другого масштаба.
Исходной предпосылкой теории подобия служит то, что подобные явления описываются одинаковыми уравнениями. Выше были рассмотрены общие уравнения переноса массы, тепла и количества движения. На практике приходится иметь дело с конкретными объектами моделирования и поэтому необходимо сформулировать условия, выделяющие рассматриваемое явление из общего класса явлений (условия однозначности). К ним относятся геометрическая форма и размеры системы (трубы, аппарата и т. д.), физические свойства ее (плотность, вязкость среды и др.), начальные условия (начальная скорость, температура и т. д.) и граничные условия, характеризующие свойства системы на ее границах.
Соотношения между сходственными величинами образца и модели называются константами (масштабами) подобия. Так для геометрического подобия – подобия геометрических размеров образца (l’ – длина, b’– ширина, h’– высота) и соответствующих размеров модели – l”, b”, h” получим константу геометрического подобия

Из этого выражения можно записать инварианты (симплексы) подобия, записав отношения параметров для образца и для модели, например:

Для подобия физических величин имеем константы подобия, например для кинематической вязкости и плотности:

При моделировании процессов, связанных с изменением свойств системы во времени (нестационарных) должно соблюдаться временное подобие, тогда константа временного подобия:

Константы кинетического подобия включают отношение скоростей u и ускорений a в сходственных точках объекта и модели:

Следует отметить, что подобие кинетическое (подобие планов скоростей и ускорений) может иметь место только при наличии подобия геометрического.
Динамическое подобие описывается соотношениями сходственных сил, энергий и масс для модели и объекта, причем динамическое подобие может иметь место только при наличии подобия геометрического и кинетического.
1.11 Подобное преобразование дифференциальных уравнений переноса
Перенос количества движения. Рассмотрим динамическое подобие на примере подобного преобразования уравнения Навье-Стокса (1.10) для одномерного потока (перенос количества движения). В этом случае скорость потока 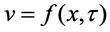 .
.
Запишем это уравнение для объекта:

Аналогичное уравнение с учетом констант подобия запишем для модели:

Чтобы уравнения (1.42) и (1.43) были идентичны, все множители из констант подобия должны быть равны, тогда:
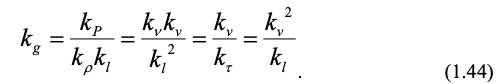
Домножив все члены уравнения (1.44) на kl /kv2, получим безразмерные соотношения:

Эти соотношения после подстановки констант подобия дают выражения соответствующих критериев подобия Фруда, Эйлера, Рейнольдса и гомохнонности. Так для критерия Фруда .

Опуская индексы, получим аналогично и другие критерии:

.
Для обеспечения подобия критерии подобия для объекта и модели должны быть численно одинаковы. Это положение определяет содержание 1-й теоремы подобия.
Так как члены уравнения Навье-Стокса представляют собой сумму удельных сил тяжести, давления, вязкости и инерции, то сравнивая их с выражениями критериев, можно сделать вывод, что критерий Фруда представляет собой отношение силы инерции к силе тяжести, критерий Эйлера – отношение силы давления к силе инерции, критерий Рейнольдса – отношение силы инерции к силе вязкости (учитывает режим движения) и критерий гомохронности – отношение инерционных сил модели и объекта (учитывает нестационарность процесса).
Обычно критерий Эйлера является определяющим и математическое описание явления переноса количества движения в критериальном виде с учетом геометрического критерия Г имеет вид:

Таким образом, решение дифференциальных уравнений описывающих процесс можно представить в виде зависимостями между критериями подобия. Это положение известно как 2-я теорема подобия.
Выше было сказано, что для обеспечения подобия критерии подобия для объекта и модели должны быть численно равны, но тогда согласно зависимости (1.46) и определяющие критерии должны быть равны. Таким образом, для обеспечения подобия достаточно равенства определяющих критериев модели и объекта. Это положение определяет содержание 3-й теоремы подобия.
Положения, устанавливаемые тремя теоремами подобия, справедливы для любого вида переноса. Они используются как для постановки экспериментов, так и для математической их обработки.
Теплоперенос. Критерии теплопереноса выводятся аналогично выводу критериев переноса количества движения. Рассмотрим подобное преобразование уравнения Фурье-Кирхгофа (1.27) для одномерного теплопереноса, когда t = f (x, τ) в отсутствии источников тепла для объекта моделирования (индексы опустим):

Аналогичное уравнение с учетом констант подобия запишем для модели:

Чтобы уравнения (1.47) и (1.48) были идентичны, все множители из констант подобия должны быть равны, тогда:

Из первого равенства выражения (1.49), подставив значения констант подобия, получим безразмерный комплекс – критерий Фурье, который характеризует изменение теплопереноса теплопроводностью во времени:

Из второго равенства выражения (1.49), подставив значения констант подобия, получим другой безразмерный комплекс – критерий Пекле, который представляет собой отношение теплопереноса за счет движения среды (конвективный) и за счет теплопроводности (молекулярный):

Он аналогичен по форме критерию Рейнольдса, который может быть рассмотрен как отношение скоростей переноса количества движения конвективного и молекулярного.
Поскольку на конвективный теплоперенос влияют условия движения среды и описывающие его дифференциальные уравнения решаются совместно с уравнениями движения потока, в критериальную зависимость, описывающую теплоперенос, должны входить и критерии гидродинамического подобия. Это критерии. Но, Fr, Re и Г. Критерий Эйлера обычно не входит в эту зависимость, т. к. не является определяющим для теплопереноса.
Так как в критерии Fr и Re входит скорость, используется их комбинация – критерий Галилея, не содержащий скорости:

или критерий Архимеда, включающий отношение плотности одной среды и разности плотностей двух сред:

Если разность плотностей вызвана термическим расширением среды (T – коэффициент термического расширения), то:

,
где Т – абсолютная температура.
После подстановки этого соотношения в критерий Архимеда получим критерий Грасгофа:

Для газов 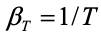 ,
,
тогда критерий Грасгофа примет вид:

При сочетании критерия Рет с критерием Re получим критерий Прандтля, характеризующий теплофизические свойства среды или соотношение полей скоростей и температур:

Если граничным условием теплопереноса является линейность теплового потока – уравнение (1.23) тогда в сочетании с уравнением (1.29) получим:

Из этого соотношения, переходя к размерным величинам, получим критерий Нуссельта, характеризующий подобие граничных условий:

Критерий Нуссельта рассматривают также как безразмерный коэффициент теплопереноса, поэтому он является определяющим. С учетом рассмотренных критериев перенос тепла можно рассматривать в виде следующей критериальной зависимости:

Для стационарного теплопереноса из зависимости (1.60) исключаются критерии. Но и Foт, содержащие время.
Критерий Nu является наиболее удобной величиной для расчета молекулярного переноса или переноса в ламинарном движении [10]. В случае развитой турбулентности более удобным оказывается использование критерия Стентона:

Тогда в зависимости (1.61) определяющим критерием вместо Nu будет критерий Stт.
Массоперенос. Критерии массопереноса и общая критериальная зависимость выводятся аналогично теплопереносу. Для этого рассмотрим подобное преобразование дифференциального уравнения массопереноса (1.22). Для одномерного потока, когда С = f (x, τ) в отсутствии источников для объекта моделирования запишем (индексы опущены):
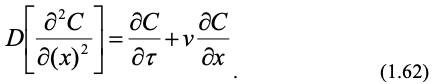
Аналогичное уравнение с учетом констант подобия запишем для модели:

Чтобы уравнения (1.62) и (1.63) были идентичны, все множители из констант подобия должны быть равны, тогда:

Из первого равенства выражения (1.64), подставив значения констант подобия, получим безразмерный комплекс – диффузионный критерий Фурье, который характеризует изменение молекулярного массопереноса во времени

Из второго равенства выражения (1.64), подставив значения констант подобия, получим другой безразмерный комплекс – диффузионный критерий Пекле, который представляет собой отношение массопереноса за счет движения среды (конвективный) и за счет молекулярной диффузии (молекулярный)

Он аналогичен по форме критерию Рейнольдса, и тепловому критерию Пекле.
Поскольку на конвективный массоперенос влияют условия движения среды и описывающие его дифференциальные уравнения решаются совместно с уравнениями движения потока, в критериальную зависимость, описывающую массоперенос, должны входить и критерии гидродинамического подобия. Это критерии. Но, Fr, Re и Г. Критерий Эйлера не входит в эту зависимость, т. к. не является определяющим для массопереноса.
При сочетании критерия Ре с критерием Re получим критерий Шмидта (в отечественной литературе его часто называют диффузионным критерием Прандтля), характеризующий соотношение молекулярного переноса количества движения и молекулярной диффузии или соотношение полей скоростей и концентраций:

Если граничным условием массопереноса является линейность потока вещества – уравнение (1.18), тогда в соответствии с уравнением (1.32) получим равенство:

Из этого соотношения, переходя к размерным величинам, получим критерий Шервуда (в отечественной литературе его часто называют диффузионным критерием Нуссельта), характеризующий подобие граничных условий при массопереносе:

Критерий Шервуда рассматривают также как безразмерный коэффициент массопереноса, поэтому он является определяющим. С учетом рассмотренных критериев перенос вещества можно рассматривать в виде следующей критериальной зависимости:

Для стационарного массопереноса из зависимости (1.70) исключаются критерии. Но и Fo, содержащие время.
Критерий Sh является наиболее удобной величиной для расчета молекулярного переноса или переноса в ламинарном движении [6]. В случае развитой турбулентности более удобным оказывается использование диффузионного критерия Стентона, т. к. он в этом случае близок к постоянному значению

Тогда в зависимости (1.70) определяющим критерием вместо критерия Sh будет критерий St. Общий вид зависимости при этом сохранится.
1.12 Внешняя и внутренняя задачи
Все процессы переноса количества движения, массы и тепла можно рассматривать в условиях внешней и внутренней задач.
Внешней задачей рассматриваются процессы переноса при обтекании тела потоком, причем размеры потока можно считать бесконечно большими. Роль линейного размера l при этом будет играть размер обтекаемого тела.
Примером внешней задачи при переносе количества движения является движение тела в бесконечной среде. Примером внешней задачи при теплопереносе является внешний теплообмен при обтекании средой горячей трубы. Примером внешней задачи при массопереносе является растворение кристалла при обтекании его потоком жидкости.
Внутренней задачей рассматриваются процессы переноса внутри твердого тела или внутри трубы, аппарата, канала. Роль линейного размера l при этом будет играть внутренний размер тела, трубы, аппарата или канала.
Примером внутренней задачи при переносе количества движения является движение среды (газ, жидкость) в трубе. Примером внутренней задачи при теплопереносе является теплопроводность внутри пластины при ее нагревании или охлаждении. Примером внутренней задачи при массопереносе является изменение влажности пористого материала при обтекании его (сушке) потоком горячего воздуха.
Необходимо отметить, что поскольку условия переноса (граничные условия) во внешней и внутренней задачах различны, решения дифференциальных уравнений и значения критериев для этих задач также будут различными. Так, например, при движении шара в сплошной среде ламинарный режим сохраняется до значения критерия Рейнольдса равном 2, а при движении среды в трубах – до значения 2100 – 2300.
Следует отметить, что явления переноса часто протекают одновременно во внешней и внутренней задаче и очень важно определить, какая из них в наибольшей степени определяет перенос (лимитирует). Примером совместной внешней и внутренней задач при переносе количества движения является движение капли, пузырька в сплошной среде. Внешняя задача – обтекание объекта потоком, а внутренняя задача – циркуляция жидкости (газа) внутри капли (пузырька). Следует отметить, что внутренняя циркуляция может значительно снизить скорость движения тела. Если влияние внешней и внутренней задач при переносе количества движения одного порядка, то говорят о смешанной задаче.
Примером совместной внешней и внутренней задач при теплопереносе является теплопередача через стенку (Рис. 1.5). Здесь внешняя задача – конвективный теплоперенос от среды к стенке, а внутренняя – теплопроводность внутри стенки. Если лимитирует теплопроводность (материал стенки теплоизолирующий), то коэффициент теплопередачи по уравнению (1.31). К , т. е. конвективными сопротивлениями можно пренебречь. Теплопередачу в условиях совместной внешней и внутренней задач характеризует тепловой критерий Био (аналог критерия Нуссельта)

Если в критерии Нуссельта оба параметра α и относятся к одной среде, то в критерии Био α – определяет конвективный теплообмен от среды к стенке (или наоборот) – внешняя задача, а параметр / l – определяет теплопроводность стенки – внутренняя задача. Если Biт 0, то лимитирует внешняя задача, если Biт → ∞, то лимитирует внутренняя задача. Если влияние внешней и внутренней задач при теплопередаче одного порядка, то говорят о смешанной задаче передачи тепла.
Примером совместной внешней и внутренней задач при массопереносе является процесс конвективной сушки пористого материала. Изменение влажности пористого материала происходит при его сушке потоком горячего воздуха. Здесь внешняя задача – конвективный массоперенос от среды к материалу, а внутренняя – перенос влаги (массопроводность) внутри материала. Перенос влаги внутри материала может быть учтен коэффициентом диффузии D внутри материала. Если лимитирует массоопроводность, то процесс массопередачи определяет диффузия внутри материала, т. е. конвективным массопереносом можно пренебречь. Массопередачу в условиях совместной внешней и внутренней задач характеризует диффузионный критерий Био (аналог критерия Шервуда)

Однако, если в критерии Шервуда оба параметра и D относятся к одной среде, то в критерии Био – определяет конвективный массооперенос от материала к среде (или наоборот при сорбции) – внешняя задача, а параметр D / l – определяет массопроводность материала – внутренняя задача. Если Bi → 0 (практически при Bi 0,2), то лимитирует внешняя задача, если Bi → ∞ (практически при Bi 50), то лимитирует внутренняя задача. Если значения критерия Био лежат в интервале от 0,2 до 50, то имеет место смешанная задача и влияние обеих внешней и внутренней задач существенно, одного порядка [10].
1.13 Критериальные зависимости стационарного переноса
Перенос количества движения. Рассмотрим примеры стационарного переноса количества движения. Внутренней задачей гидродинамики является описание движения жидкостей и газов в трубах. Для стационарного горизонтального движения в трубах (отсутствуют критерии Фруда и гомохронности) критериальную зависимость (1.46) записывают в виде

где геометрический критерий представляет собой отношение длины L к диаметру d трубы. Функциональную зависимость критерия Рейнольдса называют коэффициентом гидравлического сопротивления в трубах и обозначают

Подставив выражение критерия Эйлера в (1.74), получим уравнение Дарси:

Можно показать [6], что в ламинарном режиме (Re 2100):

а в развитом турбулентном режиме для гладких труб (Re 10000) применяется зависимость Блазиуса:

Для шероховатых труб (Δ – высота выступов шероховатости) и переходного режима [6] используют зависимости общего вида:

Примером внешней задачи переноса количества движения является стационарное движение сферических частиц в сплошной среде. В критериальной зависимости (1.46) в этом случае отсутствуют критерии Фруда, гомохронности и геометрический, т. к. сферическая частица имеет только один линейный размер – диаметр. Эта зависимость примет вид:

Равномерное движение частиц обусловлено равновесием сил, действующих на частицу – тяжести, архимедовой и сопротивления среды [6]:

где Сх – коэффициент лобового сопротивления частицы.
С учетом, что потери давления при обтекании частицы равны отношению силы сопротивления к сечению частицы

получим из (1.79):
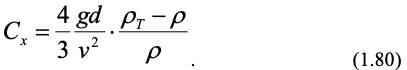
Таким образом, движение частицы сводится к зависимости коэффициента лобового сопротивления Сх от числа Рейнольдса. В ламинарном режиме (Re 2) движение частицы описывается законом Стокса ,
,
в переходном (2 Re 500), – 
а в турбулентном (500 Re 2105) Сх практически не зависит от Re и составляет Сх = 0,44.
Теплоперенос. Рассмотрим примеры описания стационарного теплопереноса в трубах и каналах (внутренняя задача) критериальными уравнениями. В этом случае общая критериальная зависимость (1.60), в пренебрежении влиянием силы тяжести, записывают в следующем виде (отсутствуют критерии Грасгофа, Фурье и гомохронности):

Конкретный вид зависимости (1.81) для ламинарного режима найден Левеком [10]:

Для труб большой длины в установившемся ламинарном режиме, при (Реd/L) 20 величина Nu стремится к постоянному значению 3,695 теоретически полученному Нуссельтом.
Для турбулентного течения в трубах (Re 10000) при отношении L/d 50 в литературе используется уравнение:

Для газов последний множитель в уравнении (1.83) равен единице и Pr зависит только от атомности газа. Так для воздуха в этом случае получим:

Для стационарного теплопереноса при обтекании тел (внешняя задача) вид зависимости (1.83) сохраняется. Так при перпендикулярном обтекании коридорных и шахматных пучков труб при Re 1000 используется уравнение:

а для обтекания шахматных пучков труб при Re 1000 применяется уравнение:

Для газов последний множитель в уравнении (1.86) равен единице и Pr зависит только от атомности газа. Для воздуха в этом случае получим:

Массоперенос. Рассмотрим примеры описания стационарного массопереноса критериальными уравнениями. В этом случае, в пренебрежении влиянием силы тяжести, общая критериальная зависимость (1.70) записывается в следующем виде (отсутствуют критерии Архимеда, Фурье и гомохронности)

Конкретный вид зависимости (1.88), например, для адсорбции на насыпном активированном угле с размером частиц 1,7-2,2 мм при средней скорости потока 0,3-2 м/с имеет вид

Аналогичный вид зависимости с близкими численными значениями коэффициентов приведен [6] для адсорбции в кипящем слое активированным углем паров четыреххлористого углерода.
Если одновременно имеет место тепло- и массоперенос (например, при сушке твердых материалов), то для расчета процесса необходимо использовать критериальные уравнения для тепло- и массопереноса.
1.14 Сушка как процесс тепломассопереноса
Сушка (обезвоживание) – это процесс удаления путем испарения влаги при нагревании высушиваемого материала и отвод образующихся паров. Таким образом, при сушке происходит тепло- и массоперенос. Сушка является в значительной степени более энергоемким процессом, по сравнению с другими видами обработки материалов. Применение неправильно выбранных режимов или конструкций аппаратов при сушке того или иного материала приводит к удорожанию и выпуску конечного продукта неудовлетворительного качества. Поэтому важно математическое описание этого процесса и выбор наиболее рациональной конструкции сушилки, а также выполнение точного расчета всех параметров сушки и последующее строгое соблюдение режима сушки на действующем сушильном оборудовании.

Рис. 1.7 Виды сушки материалов различного агрегатного состояния.
Процессу сушки могут быть подвергнуты твердые материалы, растворы (путем выпаривания) и газы (осушка газов). Схематично классификация видов сушки представлена на Рис. 1.7. Наиболее часто используется и поэтому более подробно рассматривается в данной монографии сушка твердых материалов.
Подвергаемые сушке материалы поступают в сушильные установки часто после предварительного удаления влаги, а иногда и минуя эту стадию. Начальная влажность материала, в целях экономии энергозатрат на сушку, должна быть возможно более низкой. Чем она ниже, тем меньшее количество воды потребуется удалить в процессе сушки. Поэтому перед сушкой избыточную воду из материала по возможности удаляют.
Влага из материалов может быть удалена различными способами: 1) механическим: 2) физико-химическим; 3) собственно сушкой.
При механическом удалении влага отжимается механически: путем отжима, прессования, фильтрования или центрифугирования (под действием центробежной силы в центрифугах). Механическое обезвоживание применяется для материалов, допускающих деформацию (ткани, войлок, волокнистые материалы, торф и т. п.). В текстильной, пищевой промышленности и производствах химических волокон, например, для этой цели используются фильтр-прессы, вакуум-фильтры и центрифуги. Механически удаляется только часть влаги, содержащейся в материале. После механического удаления обычно применяется дополнительная обработка влагоудаления из материала (тепловая и др. виды сушки).
Физико-химические способы сушки основаны на применении водоотнимающих средств. Эти способы не получили применения в производстве, но применяются в лабораторной технике (обезвоживание над серной кислотой, над хлористым кальцием в эксикаторах, силикагелем).
На Рис. 1.8 показаны разные способы удаления влаги из материалов с их детализацией: механический способ удаления влаги, физико-химический и удаление влаги способом сушки. Обычно при сушке из материала удаляется поверхностная влага в начале процесса, а затем и внутренняя. В ряде производственных процессов из материала могут удаляться и органические растворители (ацетон, бензин и др.), например, в производствах химических волокон при сухом и мокром формовании, в производстве искусственной кожи, нефтепереработке. Многие виды сушилок и методы их расчета могут быть использованы как для удаления влаги, так и для процессов удаления органических растворителей.

Рис. 1.8 Способы удаления влаги из материалов.
Коэффициент массоотдачи при сушке плоских материалов для периода с постоянной скоростью процесса может быть определен из следующего критериального уравнения:
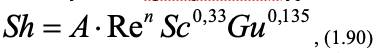
где определяющим размером при вычислении критериев Sh и Re является длина поверхности испарения в направлении движения сушильного агента. В уравнение (1.90) входит параметрический критерий Гухмана:

где tc и tм – температуры сухого и мокрого термометров.
Величины коэффициентов А и n в уравнении (1.90) зависят от режима движения сушильного агента, определяемого критерием Рейнольдса. Эта зависимость в форме таблицы представлена ниже.
Таблица 1.1 Коэффициенты критериального уравнения сушки

При тепломассопереносе в процессе сушки уравнения тепло- и массопереноса взаимосвязаны. Поток тепла q, подводимый для удаления влаги из материала, может быть найден как произведение потока массы удаляемой влаги J на теплоту парообразования r:

или с учетом уравнений (1.29) и (1.32):

В периоде постоянной скорости сушки скорость сушки с поверхности материала F, с учетом соотношения (1.93) может быть найдена как: 

где Δt – разность температуры греющего агента и температуры поверхности материала, ΔС – разность концентраций влаги у поверхности материала и в потоке сушильного агента (вместо разности концентраций часто берут разность давлений водяного пара у поверхности материала и парциального давления водяного пара сушильного агента).
При конвективной сушке температура поверхности материала близка к температуре мокрого термометра. При кондуктивной сушке температура поверхности материала близка к температуре кипения жидкости. При других способах сушки и при комбинированной сушке температура поверхности материала находится между этими значениями температур.
Как следует из уравнения (1.94), скорость сушки в первом периоде можно определить как из уравнения тепло-, так и из уравнения массопереноса. Коэффициенты α и находят из соответствующих критериальных уравнений.
Предваряя рассмотрение макрокинетики конкретных процессов сушки, рассмотрим сначала свойства применяемых теплоносителей (сушильных агентов) и свойства высушиваемых материалов, как объектов участвующих при обработке материалов в процессе сушки.