3 Месопотамия
МЕСОПОТАМСКАЯ ЦИВИЛИЗАЦИЯ
Пути развития астрономии в Месопотамии, по крайней мере в течение того долгого периода, о котором мы можем судить по письменным источникам, настолько радикально отличались от всего сделанного египтянами до этого, а греками и индусами – после, что кажется вполне естественным провести различие между ними. Поступая таким образом, мы рискуем сыграть на руку ошибочному убеждению о якобы простоте и монолитности этих культур в своей основе. Вопросы общего космологического значения – составная часть мифологий всех народов, при этом они обладают необозримым количеством местных различий. Несовпадение языков является естественным препятствием для взаимопроникновения идей, и на Ближнем Востоке говорили на многих языках, но чувство гордости и ощущение идентичности населявших его народов были настолько сильны, что даже соседние города, говорившие на одном языке, часто поклонялись различным планетным божествам. При таких обстоятельствах и ограничениях, налагаемых объемом книги, можно лишь кратко охарактеризовать этот регион, но есть как минимум одно положение, о котором нужно постоянно помнить. Все современные науки, использующие математические методы, находятся в долгу у вавилонских астрономов, особенно тех, кто жил в период, начавшийся в V или VI в. до н. э., и стал свидетелем расцвета месопотамских достижений. А если так, то за всеми различиями мы должны найти нечто, свойственное месопотамской астрономической практике как единому целому.
В VI в. до н. э. Вавилон на короткое время обрел независимость после долгих лет подчинения ассирийцам. С падением Ассирийской империи вавилоняне начали работу по возрождению своего утраченного величия, которым они обладали за тысячу лет до этого, когда ими правил Хаммурапи (примерно в 1792–1750 гг. до н. э.). Однако мощь персов росла не менее стремительно, и в 539 г. до н. э. Кир Великий нанес сокрушительное поражение Набониду – последнему вавилонскому царю. Многие знакомы с последствиями этих событий по библейскому описанию освобождения израильтян, покоренных Вавилоном после того как Навуходоносор II разрушил Иерусалим.
Наконец, Персидская империя была разгромлена Александром Великим, что привело к значительному упрочению связей с греческой культурой. Александр вошел в Вавилон в 331 г. до н. э. После его смерти в 323 г. и распада империи Вавилон пришел в упадок в результате перипетий, случившихся во время правления Селевка – наиболее способного политического преемника Александра, основавшего новую династию. Селевк создал условия для устойчивого притока греческой иммиграции в эту новую греческую и македонскую империю в Азии. Когда мы говорим о «греческой учености» в широком смысле, то начиная с этого времени мы должны принимать во внимание не только города-государства Балканского полуострова и окружающих его островов, но также широкий культурный регион Средней Азии, не говоря уже об Александрии и эллинизированном Египте.
Имея в виду эти события, представляется полезным разграничить четыре исторических периода: первый – это династия Хаммурапи и все, что было до нее; второй – ассирийский период (1000–612 гг. до н. э.); третий – период независимости (612–539 гг. до н. э.) с последующим подчинением Персии (539–331 гг. до н. э.); и последний – период Селевкидов (331–247 гг. до н. э.).
ВАВИЛОНСКАЯ АСТРОНОМИЯ ВРЕМЕН ДИНАСТИИ ХАММУРАПИ
В течение последних полутора столетий археологи раскопали несколько месопотамских храмов с характерными массивными ступенчатыми башнями, известными как зиккураты. Например, в Уруке обнаружен комплекс, постройка которого восходит к четвертому тысячелетию, а в древнем шумерском городе Эриду отдельные строения вполне можно отнести к пятому тысячелетию до н. э. Древнейшие записи обнаружены в этих храмах и, судя по всему, именно в них была сосредоточена политическая власть. Они владели большей частью пахотных земель и играли ведущую роль в управлении ирригацией. Хотя остается неясным механизм связи религиозной властной элиты с властью светских правителей, нет никаких сомнений в том, что крайне сложный бюрократический аппарат вырос и окреп внутри духовенства. Не позднее чем в третьем тысячелетии до н. э. шумеры изобрели клинописный шрифт – способ письма, когда знаки выдавливаются с помощью клинообразной палочки – стиля – на мягкой глине, которая затем выставляется на солнце для просушки. Вавилоняне, относящиеся к семитским народностям, использовали эту технику и адаптировали ее к своему языку посредством комбинирования фонетической орфографии с шумерскими идеограммами.

25
Клинописная форма записи числа 23
Они также переняли шумерскую систему счисления, и это имело неоценимое научное значение, поскольку в ней использовалась позиционная форма записи, подобная используемой в нашей современной системе (в отличие от римских чисел). Различие заключается в том, что мы работаем с десятичной системой, а у них основание равнялось шестидесяти. Эта шестидесятеричная система появилась в третьем тысячелетии. Числа до 60 записывались обычным образом, наподобие римских цифр, по принципу повторения клинообразных знаков для десятков и вертикальных штрихов для единиц. (См., например, запись числа 23 на ил. 25.) После 60 знаки разделялись пробелами. Если заменить пробелы запятыми, то, например, число 2,9,14 будет означать:
Сложности в этой системе могут возникать, когда такая же последовательность чисел используется для дробей. Это свойственно и нашему десятичному представлению, где употребление последовательности 3546 может в равной мере означать и 3546, и 345,6, и 35,46 и т. д. Возникает потребность в каком-нибудь пунктуационном знаке, чтобы отделить дробную часть от целой, и современные авторы договорились употреблять в этом случае точку с запятой. Так, последовательность чисел 2,7,17;52,13 может теперь быть использована для представления шестидесятеричного числа:
Вероятно, перевод нашего десятичного представления в столь мощную систему, как вавилонская, может показаться неудобным, однако такая комбинированная форма записи не должна вызывать слишком серьезных затруднений, поскольку мы пользуемся вавилонским наследием всякий раз, когда записываем время в часах, минутах и секундах или углы – в градусах, минутах и секундах и т. д. Характеризуя их систему как «мощную», мы имеем в виду то, что число 60 имеет много простых множителей. (Счет по пальцам, определяемый эволюционным развитием, был бы совместим с этой системой, окажись мы обладателями 12 или даже 30 пальцев.)
Шумеры, а вслед за ними и вавилоняне, искусно применяли эту систему счисления. Для упрощения расчетов они придумали одно из наиболее полезных научных изобретений, а именно – таблицы чисел. Они располагали таблицами умножения, таблицами для взаимно обратных величин, для площадей и даже для квадратных корней. Вавилоняне были экспертами в проведении вычислений, которые мы без тени смущения можем назвать алгебраическими. Они умели решать линейные и квадратные уравнения, и даже частные случаи уравнений с более высокими степенями. Они доказывали алгебраические формулы геометрически, делая это почти так же, как мы, если иметь в виду греческую традицию. Такие технические приемы широко использовались в период первой вавилонской династии, начавшейся с правления Хаммурапи, «законодателя», и длившейся три столетия. (Эта династия прекратила свое существование не позже 1531 г. и, по мнению некоторых специалистов, не ранее 1651 г.) Все свидетельства указывают на относительную многочисленность образованных жрецов, являвшихся первоклассными экспертами в области арифметики, и этот факт крайне важен для подаренного ими миру типа астрономии.
Самый ранний письменный период месопотамской истории свидетельствует об огромном разнообразии местных культов, распространявшихся по мере изменения политической власти и передававшихся от древнейших шумерских народов вплоть до их семитских преемников. Многие боги не имели никакого отношения к небу, но в городе Уре почитали местное божество по имени Син – бога Луны; в городах Ларса и Сиппар чтили Шамаша – бога Солнца (ил. 26); а в некоторых других поклонялись богине Иштар, позже отождествляемой с планетой Венерой, но сначала, по всей видимости, олицетворявшей плодородие. В самом Вавилоне, после того как Хаммурапи объединил всех богов городов-государств в единый пантеон, хранили верность Мардуку – богу, наделенному превосходством верховного «Творца». Вавилонский миф о сотворении мира «Энума элиш» («Когда наверху») ежегодно декламировался в четвертый день новогоднего празднества, проводимого в Вавилоне во время первых двенадцати дней месяца нисан. Он повествует о том, как бог Мардук возвысился до царствования над другими богами, победив силы хаоса, персонифицированные в богине моря Тиамат. Затем он, по преданию, создал мир и построил город Вавилон, сделав его земным обиталищем богов.
Не всех богов можно каким-либо образом идентифицировать со звездами: трое высших – Ану, Энлиль и Эа – соответствовали небу, земле и воде. Однако есть все основания полагать, что древние вавилонские боги были, по преимуществу, космическими в той или иной своей ипостаси. Проявление глубокого интереса к космическим вопросам напрямую следует из дошедших до нас древнейших литературных произведений. Вавилонский эпос о Гильгамеше содержит косвенные упоминания о ритуальных наблюдениях Солнца, Луны и планет над вершинами далеких гор.

26
Верхняя часть «Таблички бога Солнца» из Сиппара (в настоящее время хранится в Британском музее). В пространном клинописном тексте, расположенном под этим изображением (отсутствующем на приведенной иллюстрации), Набу-апла-иддин описывает, как он реставрировал древнее изображение бога Солнца и его храм (ок. 870 г. до н. э.). На иллюстрации царя подводят к алтарю, на котором покоится солнечный диск Шамаша.
Потрясенный смертью своего друга, Гильгамеш отправляется в путешествие и приходит к горе Машу, «Чьи вершины небесного свода достигают, / Чьи основания нижней части преисподней достигают». Там он возносит молитву Луне (Сину), прося у нее защиты. В этих горах находились ворота, через них Солнце отправлялось в свое дневное путешествие. Ворота стерегли два человека-скорпиона – муж и жена, они впустили Гильгамеша. Он шел одиннадцать часов в абсолютной темноте, а на двенадцатом увидел свет, появившийся у выхода по другую сторону гор, где он попал в прекрасный сад с растениями из драгоценных камней. Гильгамеш отыскал цветок, дарующий бессмертие, но его утащила и проглотила змея, которая, сбросив кожу, обновила свою жизнь – аллегория, предположительно, относящаяся к движению Солнца. Считалось, будто Солнце, как змея, обладает властью обновлять свою жизнь, но Гильгамешу было отказано в такой возможности. В целом печальный посыл всего этого эпического произведения понятен: человек смертен.

27
Еще в пятом тысячелетии до н. э. торговцы с берегов Тигра и Евфрата накладывали на глину оттиски для опечатывания дверей, сосудов и других емкостей. После XXXV в. до н. э. были в ходу искусно гравированные цилиндрические печати, которые прокатывали по глине, чтобы оставить на ней отпечаток. На рисунке изображен оттиск, оставленный печатью, относящейся к Аккадской династии (третье тысячелетие). Он содержит довольно распространенное изображение, связанное с эпосом о Гильгамеше (в настоящее время хранится в Британском музее). На рисунке бог Солнца Шамаш, которого можно узнать по исходящим от плеч лучам и пиле в руке, поднимается из седловины, образуемой двумя вершинами горы Машу.
Месопотамские цилиндрические печати (гравированные цилиндры, размером с колпачок от ручки; ими прокатывали по мягкой глине и на ней оставалось какое-либо изображение) подтверждают догадку, что отдельные элементы этой истории были хорошо известны. На них часто изображается бог Солнца, ступивший в горный проход между двумя воротными столбами, и иногда потрясающий ключом от ворот. На воротах сидят львы – распространенный атрибут Солнца, а от плеч божества исходят солнечные лучи. В окрестностях Вавилона нет гор, которые можно увидеть из долины Тигра; небольшие горы, откуда мог прийти культ поклонения богу Солнца, есть на востоке – в Эламе (в районе города Сузы) или в гористой местности, простирающейся к северо-западу от Вавилона, на территории современной Турции. Бог Солнца изображался с пилой, и, если не поднимался, опираясь на собственные руки, то стоял, опершись одной ногой на гору (ил. 27). Как видно из более поздних изображений (ок. 1800 г. до н. э.), горы были заменены на структуры, больше похожие на пни, что лучше соответствовало особенностям вновь освоенных территорий. Это указывает на важность местных обстоятельств. Они частично влияли как на мифологию, так и, в равной степени, на религиозные техники наблюдений за небом.
При Хаммурапи унифицировали не только пантеон, но и календарь, и месяцам присвоили вавилонские названия. Поскольку продолжительность месяца близка, но не равна в точности 29,5 суткам, и поскольку количество месяцев в солнечном году не является целым числом (оно равно примерно 12,4), любой календарь, предполагающий их совместное использование, нуждался в правилах интеркаляции. Такие правила были установлены, и, согласно им, месяц должен содержать 29 либо 30 дней, а год – 12 либо 13 месяцев. Хотя они далеки от совершенства, и их применение не носило универсального характера, этими правилами продолжали пользоваться вплоть до 528 г. до н. э. На протяжении всей истории встречаются примеры тесных отношений между календарем и культурой; каждая династия – или, в других случаях, каждая религия или религиозная секта – стремится использовать собственный календарь. Поэтому особый интерес представляет обнаружение письма Хаммурапи, в котором он сообщает адресату о своем решении вставить в календарь дополнительный месяц. В письме указывалось, что это распространяется и на сбор налогов. Ухищрение, похоже, не имеющее параллелей в современной истории.
Вавилонян очень часто, и не всегда из лучших побуждений, причисляли к астрологам. Смысл, обычно вкладываемый в это слово, появился в относительно поздний период и в гораздо большей степени обязан греческому влиянию; однако не вызывает сомнений, что большинство вавилонских предсказаний самого раннего периода носило космический характер. Конечно, далеко не все предзнаменования являлись астральными. Например, созвездия, Солнце, Луна и Венера были так или иначе связаны с богами, но существовало и множество земных божеств. До нас дошла очень большая серия предзнаменований – всего около семи тысяч, – содержащая многие тысячи самых разных явлений, каждое из которых могло стать предметом толкования. Эта серия известна по ее начальным словам как «Энума Ану Энлиль…» (Когда боги Ану и Энлиль…). Предзнаменования дошли до нас в табличках, относящихся ко времени, когда Вавилоном правили касситы (приблизительно 1500–1250 гг. до н. э.), но многие из них с большой вероятностью скопированы с более ранних источников, включая Аккадскую династию (около 2300 г. до н. э.). Даже за несколько столетий до начала новой эры существовал класс людей, известных как «писцы Энума Ану Энлиль». Многие из предзнаменований учитывали астрологическое значение положений и появлений планеты Венеры. Шестьдесят третья табличка этой серии на деле представляет собой наиболее важный из всех ранних астрономических документов, поскольку в ней содержится описание методов расчета появления и исчезновения Венеры и астрологические интерпретации этих событий.
Таблички с материалами наблюдений Венеры (их различные сохранившиеся копии) связывают с эпохой царя Амми-цадуки, чье правление началось спустя 146 лет после начала правления Хаммурапи. В главе 2 мы ввели понятие гелиакических восходов и заходов неподвижных звезд. В табличках Амми-цадуки приведен практически полный перечень гелиакических восходов и заходов планеты Венера за 21 год, и к каждому из этих событий прилагались астрологические толкования, касающиеся перемен в климате и ратных делах, голода и эпидемий, судеб царей и наций.
ПЛАНЕТНЫЕ ДВИЖЕНИЯ: ОТСТУПЛЕНИЕ
Прежде чем начать обсуждать эти знаменитые таблички, мы должны сделать отступление для объяснения рассматриваемых в них движений с современной точки зрения. Хотя это и не соответствует древним представлениям о данном предмете, но чтобы вспомнить особенности этих движений, полезно рассмотреть их, располагая Солнце в центре планетной системы. Общий принцип обращения вокруг Солнца всех планет, видимых невооруженным глазом, останется прежним: если смотреть на Солнечную систему со стороны северной части неба, то планеты будут двигаться против часовой стрелки. (Речь идет о долгопериодическом движении, не имеющем ничего общего с мнимым суточным движением – восходами и заходами, происходящими в результате вращения Земли вокруг своей оси. Ил. 28 иллюстрирует излагаемые здесь базовые положения.) Безусловно, планета, наблюдаемая с какого-либо места в Северном полушарии Земли, будет ежедневно вставать и садиться, но если в течение долгого времени наблюдать ее движение на фоне неподвижных звезд, то в большинстве случаев она будет медленно смещаться влево, в сторону, противоположную суточному движению. Тогда каждый следующий день она будет восходить чуть позже, чем в предыдущий. Это же справедливо и для Солнца, поскольку, после минутного размышления, станет понятно: если Земля обращается вокруг Солнца против часовой стрелки, то и Солнце, наблюдаемое с Земли, будет обращаться вокруг нас тоже против часовой стрелки. Этот тип движения на фоне звезд называют «прямым». Забегая вперед, скажем, что именно поэтому положения планет и звезд «по долготе», записанные в эклиптических, или экваториальных, координатах, будут систематически увеличиваться.

28
С чисто геометрической точки зрения Солнечную систему можно рассматривать и как гелиоцентрическую, и как геоцентрическую, хотя и не с такими принятыми в древности геометрическими допущениями. Земля, как и остальные планеты, обращается вокруг Солнца, мало чем отличаясь от них в этом смысле. (Для простоты здесь изображены только четыре орбиты, причем все они предполагаются круговыми.) Мы можем без ущерба для всей конфигурации связать неподвижный центр этой системы с Землей. Можно предположить далее, что Солнце обращается вокруг Земли (также в направлении, противоположном движению часовой стрелки, как это показано на рисунке), а все другие планеты следуют за ним, и в центрах их орбит расположено Солнце.
Обычно планеты движутся относительно звезд в прямом направлении, но иногда они начинают двигаться в противоположную сторону. Такое движение называют «попятным». Венера находится ближе к Солнцу, чем мы, и поэтому может располагаться между нами и Солнцем, или по другую сторону от него. Когда Венера находится за Солнцем, она движется в прямом направлении, поскольку ее собственное прямое движение складывается с прямым движением Солнца. Однако, когда она приближается к нам, у нее появляется попятное движение (перемещение слева направо, если наблюдать с севера), так как при наблюдении с Земли оно оказывается более быстрым, чем прямое движение Солнца (справа налево). Есть положения, когда она будет казаться неподвижной для земного наблюдателя. На ил. 29 они помечены точками MS и ES (предполагается, что линия, соединяющая Солнце с Землей, неподвижна). В первой точке стояния планета видна утром, непосредственно перед рассветом, но вечером она зайдет за горизонт раньше Солнца, и потому будет невидима. Когда Венера находится в другой точке стояния ES, она видна только по вечерам, после заката, а утром взойдет после Солнца, скрытая его лучами.

29
Конфигурации Венеры, нижней планеты (то есть планеты, находящейся внутри орбиты Земли). Соотношение относительных размеров орбит на рисунке близко к реальному. Меркурий – другая нижняя планета – движется аналогично.
Приближаясь к верхнему соединению, помеченному на рисунке точкой SC, или нижнему соединению, IC, Венера становится невидимой, поскольку и в том и в другом случае ее затмят солнечные лучи. Чтобы стать доступной наблюдению, она должна находиться на расстоянии примерно 10° от Солнца. (Величина этого угла зависит от многих факторов, но у нас пока нет нужды вдаваться в эти подробности.) На рисунке точки MF и ML обозначают положения, когда Венера наблюдается первый и последний раз в виде утренней звезды; а EF и EL – точки ее первого и последнего появления в виде вечерней звезды.
Полный цикл движения Венеры относительно Солнца длится 584 дня. Период, в течение которого она остается невидимой, зависит от нескольких факторов, таких как географическая широта и время года. По очень грубой оценке, дюжина недель невидимости в верхнем соединении и две недели в нижнем – вполне приемлемое приближение.
В числе планет, известных до открытия в XVIII в. Урана, есть еще одна, тоже расположенная между нами и Солнцем и движущаяся примерно так же, как Венера. Это – Меркурий. Орбиты верхних планет (до Урана были известны только Марс, Юпитер и Сатурн) располагаются за пределами орбиты Земли, поэтому они ведут себя иначе. Например, их можно наблюдать в полночь высоко над головой, что, очевидно, совершенно исключено для Меркурия и Венеры; однако у них равным образом могут быть попятные движения, и они в свою очередь имеют периоды невидимости, наступающие, когда их угловое расстояние от Солнца в соединении невелико.
Первые и последние появления планет вызывали у вавилонян огромный интерес. По-видимому, они стали обращать на это внимание после того, как установилась традиция наблюдения гелиакических восходов неподвижных звезд. Эти наблюдения имели огромное значение для выработки теорий, позволяющих предсказывать положения планет, поскольку они задавали точки отсчета, относительно которых можно определять положение планеты в тот или иной момент времени.
РЕЛИГИЯ И АСТРОЛОГИЯ
В табличках с информацией о наблюдении Венеры времен Амми-цадуки приведены годы, месяцы и номера дней, когда планета достигает положений EL, MF, ML и EF в течение примерно 21-летнего периода. Поэтому в конечном счете должно было выясниться, и действительно выяснилось, что последовательность этих событий почти в точности повторяется через каждые восемь лет (точнее, через каждые 99 вавилонских месяцев, за вычетом 4 дней). Это стало ясно после пяти полных циклов с четырьмя указанными событиями. Мы можем самостоятельно убедиться в справедливости этого тождества, вытекающего из равенства синодического периода Венеры (времени, затрачиваемого на один оборот вокруг Солнца относительно линии, соединяющей Солнце с Землей) 583,92 суток; пять таких периодов образуют 2919,6 суток, в то время как 8 лет, по 365,25 суток каждый, дают нам 2922,0 суток. Впоследствии астрономы извлекли много пользы из этого близкого тождества, осознав, что после первых восьми лет наблюдений будет нетрудно довольно точно рассчитать эфемериды Венеры, поскольку ее координаты почти в точности повторятся в те же дни (солнечного) календаря. Похожие циклические соотношения существуют у всех планет, но они не столь просты, как в приведенном случае.
Одна из версий этих табличек отчетливо демонстрирует, что в ней мы имеем дело не просто с последовательностью необработанных наблюдений, а с данными, складывающимися в узнаваемую схему. Например, периоды невидимости всегда указываются равными либо трем месяцам, либо семи дням, а даты разбиты по группам с равными интервалами, повторяющимися от группы к группе. (Например, планета покидает одно положение MF на второй день первого месяца и переходит в следующее положение EF на третий день второго месяца, затем в следующее положение MF на четвертый день третьего месяца и т. д.) Это служит наглядным подтверждением учета периодичности явлений, а это является крайне важной вехой в истории научной астрономии. К большому сожалению, мы не можем точно датировать эту табличку. Она была изготовлена не позже разгрома Мидасом библиотеки Ашшурбанапала в 612 г. до н. э., но вполне может быть отнесена к VIII или IX в.
Точная последовательность дат, содержащаяся в исходных табличках Амми-цадуки, позволила Б. Л. Ван дер Вардену датировать их, в результате чего он отверг две из трех вавилонских хронологий, пользовавшихся доверием историков. В его хронологии династии Хаммурапи отводятся 1830–1531 гг. до н. э., где его собственное правление приходится на 1728–1685 гг. до н. э., а правление Амми-цадуки – на 1582–1562 гг. до н. э. В целом же вопрос продолжает оставаться в высшей степени неопределенным. Часть затруднений связана с тем, что по религиозным и астрологическим соображениям венерианские таблички неоднократно переписывались в течение нескольких столетий. И даже их косвенная причастность к Амми-цадуке признавалась не всегда и не всеми. Как уже упоминалось, планета Венера отождествлялась с богиней Иштар, а календарь, по которому отмечались ее появления, основывался на движениях Солнца и Луны, а они, в свою очередь, были связаны с богами Шамашем и Сином. В те далекие времена астрологические и религиозные мотивы были неотделимы друг от друга. Считалось, что почитаемые божества, появляясь на небе, способны оказывать влияние на происходящее в делах любви, вражды и других формах человеческого поведения. («Когда Венера стоит высоко, соитие будет особенно приятным…» и т. д.) Третий аспект описываемых затруднений заключается в следующем. Как только стало возможным научное предсказание планетных положений, предугадывание событий по планетам стало следовать естественному порядку вещей. Конечно, всегда находились те, кто верил в их божественную силу. С течением времени эта религиозная вера утратила свое былое значение или вовсе исчезла, но она оставила после себя веру в возможность осуществления предсказаний с опорой только на планетные положения. Астрология без религии могла стать более научной, однако в каком-то смысле она одновременно стала менее рациональной, сделав человеческие действия зависимыми уже не от богов, обладавших человеческими качествами, а только от небесных объектов. В период классической Античности, затем в Средние века и позже астрологи напряженно трудились над тем, чтобы восстановить отдельные элементы утраченной рациональности, изобретая теории небесных влияний.
ВАВИЛОНСКАЯ АСТРОНОМИЯ В АССИРИЙСКИЙ ПЕРИОД
Хетты разгромили Вавилон в 1530 г. до н. э., но вскоре он вошел в состав империи касситов. Этот период завершился около 1160 г. до н. э., и в течение всего этого времени астрономические традиции постепенно укреплялись. Именно в этот период составлен список предзнаменований Энума Ану Энлиль – серия табличек, уже упоминавшаяся нами ранее в связи с сохранившимися табличками с материалами наблюдений Венеры времен Амми-цадуки. Вавилон уже обладал репутацией просвещенного города: еще до начала ассирийского господства ассирийцы использовали вавилонский диалект в своих произведениях. Были дополнены звездные списки, связывающие наступление нового месяца с гелиакическими восходами звезд. Их часто ошибочно называют «астролябиями», но они более известны по их ассирийскому названию «три звезды в каждом». Они обычно содержат по 36 звезд: 12 «звезд Ану», расположенных вблизи небесного экватора, «12 звезд Эа» – к югу от него, и «12 звезд Энлиля» – к северу. (В них, отметим, время от времени встречаются названия планет. Это странно, поскольку гелиакические восходы планет происходят не в одни и те же дни.) Возможно, согласно одной из современных точек зрения, «пути» трех богов не опоясывали все небо, а отмечали сектора восточного горизонта, где восходили эти звезды. Известные нам образцы «трех звезд в каждом» происходят из Вавилона, Ашшура, Ниневии и Урука. Часть этих особых табличек имела прямоугольную форму, но обнаружены и круглые, напоминавшие по внешнему виду мишень для игры в «дротики», разделенную на двенадцать секторов.
Некоторые цифры на двух таких табличках (одной прямоугольной и одной круглой) были интерпретированы как свидетельство деления вавилонянами дневного времени суток на двенадцать равных частей. То же самое они проделывали с ночью. (Сравните это со сказанным выше, на с. 57, о делении ночи и дня на двенадцать частей египтянами.) Строго говоря, такой способ деления устанавливает зависимость между продолжительностью часа и временем года. Это считалось обычной практикой во всем ближневосточном регионе, а впоследствии – и во всей Европе. Греческий историк Геродот сообщает нам, что греки переняли свой двенадцатичасовой день от вавилонян. Этот способ счета времени стал общепринятым, несмотря на свое, по всей видимости, сугубо астрономическое происхождение. С другой стороны, существовал метод «равных часов», точно отмеряемых, например, по суточному вращению небес или при помощи клепсидр. Однако даже при использовании клепсидр существовала потребность в неравных, сезонных часах, поскольку были найдены глиняные таблички с таблицами, в которых указывалось количество воды, расходуемой в течение одной ночной стражи, с разбивкой всего года на пятидневные интервалы. (Ночь делилась на три стражи.) Призма из слоновой кости, найденная в Ниневии (время происхождения VIII в. до н. э. или позже) и хранящаяся сегодня в Британском музее, показывает, что перевод между этими двумя системами счета времени, в которых использовались равные и сезонные часы, впоследствии являлся одной из задач, решаемых астрономией. Вавилонские астрономы пользовались 12-часовой системой двойных часов (беру), каждый из них делился на 30 частей (уш), то есть один уш равнялся четырем нашим минутам.
Из «трех звезд в каждом» развилась другая традиция. Ее следы мы находим в серии двухсторонних глиняных табличек, содержащих текст, представляющий собой астрономо-астрологический компендиум, известный как МУЛ.АПИН. Эта серия, как известно, была составлена из текстовых фрагментов, написанных в разные столетия, древнейший из дошедших до нас датируется VII в. до н. э. Заглавие, переводимое как «Плуг», просто воспроизводит начальные слова из списка звезд и созвездий, с них и начинается этот текст. Похоже, что набор базовых сведений изложен только в первых двух табличках. По клинописным знакам сохранившихся фрагментов можно составить полное представление о содержании первой таблички и восстановить бо́льшую часть второй. Вероятно, они включают выборку из наиболее существенных вавилонских астрономических представлений и заканчиваются небесными знамениями, взятыми целиком из начала первого тысячелетия до н. э. Современные ученые исследовали эту подборку текстов множеством разных способов; некоторые трактовали ее как серии астрономических комментариев, составленных для различных целей, другие – как набор абстрактных схем для составления предсказаний, не более. Вне зависимости от сделанных ими выводов, они обнаружили высокую степень астрономической компетенции, поскольку временами складывается впечатление, будто эти таблицы составлены для устранения противоречия, возникавшего в случае, если наблюдаемые на небе события не соответствовали предсказанному.
Были усовершенствованы прежние списки «звезд Эа, Ану и Энлиля»; составлены списки звезд с восходами, совпадающими с заходами других звезд, и для некоторых из них указан период невидимости. Таблички позволяют составить представление о названиях и структуре созвездий, используемых вавилонянами, и заимствованных в отдельных случаях у шумеров. Они не всегда совпадают с нашими, хотя в итоге благодаря посредничеству греков мы переняли бо́льшую часть из них. Например, АПИН, если подразумевать под этим словом плуг, соответствует нашему созвездию Треугольник с включением в него звезды γ Андромеды. Шумерские названия созвездий Телец, Лев и Скорпион дошли до наших дней, хотя и с небольшими изменениями. Изготовление карты звездного неба – вещь вполне заурядная, и один из ранних образцов, взятый из библиотеки Ашшурбанапала в Ниневии, несмотря на отсутствие нескольких фрагментов, отображает девять или десять узнаваемых групп звезд (ил. 30).
В реальной жизни восходы и заходы звезд в пустыне происходят не столь безукоризненно, как в голливудских фильмах об Аравии. Если на высоких широтах фактором, ощутимо влияющим на качество наблюдений, являются водяные пары (наряду с другими типами атмосферной абсорбции), то ближневосточный горизонт часто бывает скрыт за атмосферной турбулентностью и пылью. Ассирийские записи показывают, что первое появление молодой Луны часто регистрировалось, когда она была уже высоко над горизонтом. Поскольку наблюдения восходов очень часто бывали неточны, а в отдельных случаях им мешали строения, в табличках МУЛ.АПИН приводился список вспомогательных звезд (зикпу-звезд), кульминировавших (пересекавших меридиан) одновременно с восходом более фундаментальных звезд. Под «фундаментальными звездами» мы понимаем звезды, по восходу которых велся счет времени и рассчитывался календарь. Указанный список зикпу-звезд важен с научной точки зрения, поскольку он представляет собой шаг в направлении более надежного измерения времени. Например, сохранились отчеты о наблюдении лунных затмений, относящиеся ко времени не позднее VII в. до н. э., когда время определялось по кульминациям зикпу-звезд с внесением небольших дополнительных уточнений, определяемых по водяным часам. (Как уже упоминалось, единицей измерения времени был уш, соответствующий нашим 4 минутам.)
Серия МУЛ.АПИН не пользовалась зодиакальными знаками как средством деления пути Солнца среди звезд на двенадцать частей, но она оперировала в целом схожей системой, поскольку в ней приводится список созвездий на пути Луны. Похоже, речь идет о восемнадцати созвездиях, носящих имена богов, встречаемых Луной на своем пути, а не появившихся позже двенадцати знаках зодиака. Конечно, путь Луны по небу более или менее совпадает с солнечным – расхождение составляет всего лишь пять градусов, или около того, – поэтому короткий список является частью более длинного. Из текста становится ясно, что пути движения Солнца, Луны и пяти планет рассматривались как схожие. Невзирая на существование способа деления неба на восемнадцать частей, солнечный год к этому времени, определенно, делился на двенадцать месяцев.

30
Рисованная копия фрагментов карты звездного неба из библиотеки в Ниневии, основателем которой считают Ашшурбанапала, последнего из великих ассирийских царей, правившего в 668–627 гг. до н. э. На этом глиняном диске приведены клинописные названия и схематические изображения звезд и созвездий (звезды соединены линиями, как на современных картах). Против часовой стрелки снизу: Сириус (Стрела), Пегас и Андромеда (Поле и Плуг), Овен, Плеяды, Близнецы, Гидра с Вороном и Девой, Весы. Следует отметить, что небо разделено на восемь частей. (Британский музей, табличка K 8538, скопировано Леонардом Кингом [1912], исправлено Иоганном Кохом [1989].)
Другим примером того, как серия МУЛ.АПИН может свидетельствовать о возрастающем значении математики в астрономии, является список времен, когда тень от вертикального стержня (гномона) высотой в один локоть достигает 1, 2, 3, 4, 5, 6, 8, 9 или 10 локтей в длину в разные сезоны. И снова мы имеем здесь дело не с отчетом о наблюдениях в строгом смысле этого слова, а скорее с результатом некой рационализации, воплощенным в перечислении твердо установленных правил, задающих соразмерность между временем восхода Солнца и длиной тени. Проще говоря, хотя этот перечень и несовершенен, он научен в буквальном смысле этого слова, и какую бы часть этих табличек мы ни взяли, мы найдем там систематическое приведение наблюдательных данных к какому-либо рациональному порядку. Например, они содержат правила расчета времени восхода и захода Луны в зависимости от ее фазы. (Так, в новолуние она садится почти одновременно с заходом Солнца; затем ее заходы происходят с задержкой на одну пятнадцатую часть ночи в каждый следующий день; а после пятнадцатой ночи приводятся аналогичные правила, но уже для ее восходов.) Похожие правила оставались в ходу еще в эпоху Римской империи. Будучи основанным на арифметических процедурах, этот материал имел высокое практическое значение. Одна из простейших схем включения в календарь дополнительных дней основывается на определении даты первого месяца в году, когда Луна проходит через Плеяды. Согласно этому правилу, в «идеальный год» это случается в первый день. Если же это случается в третий день, то надлежит произвести интеркаляцию.
Для сравнения, процедуры, применяемые в отношении планет, были значительно примитивнее, и даже теория Луны, содержащаяся в этой работе, чрезмерно проста по сравнению с возможными достижениями того времени, когда изготовлялись копии многих из сохранившихся табличек. Они имеют давнюю историю, но, вероятно, созданы где-то на широте Ниневии в начале первого тысячелетия. Вне зависимости от точности содержащейся в них информации, они свидетельствуют о глубокой заинтересованности в разработке теоретических основ астрономии.
ВАВИЛОНСКАЯ АСТРОНОМИЯ В ПЕРИОД НЕЗАВИСИМОСТИ И ПЕРСИДСКОГО ПРАВЛЕНИЯ
Похоже, что в течение всего периода, пришедшегося на падение Ассирийской империи, возрождение вавилонского наследия при халдейском правлении, а затем персидское завоевание, интеллектуальная жизнь и религиозные искания были столь же насыщены, как и прежде. Клинописные тексты продолжали писаться на шумерском и аккадском языках, хотя в гражданской жизни и тот и другой уступили место арамейскому языку и алфавиту. Предзнаменования стали использоваться для предсказаний, осуществляемых в новом стиле – на основе гороскопов, то есть на сопоставлении с небесами того, что считалось важным в данный момент – начало путешествия, сражение, чье-либо рождение и т. д. Проводились систематические наблюдения планет, а также Луны и затмений – не спорадически, а без каких-либо значительных перерывов – вплоть до окончания эпохи Селевкидов. Описания затмений удивительно подробны и включают как числовые, так и другие характеристики, иногда даже направление дующего ветра. Записи, которые считались особенно важными, хранились в текстах селевкидских архивов. Их можно разделить на две главные категории – то, что Абрахам Закс назвал «астрономическими дневниками», и (встречающиеся гораздо реже) подборки данных, содержащие наблюдения какого-либо отдельного астрономического явления за несколько лет.
Дневники (наиболее ранние из них датируются 652 г. до н. э.) содержат описание многих «значимых» событий самого разного толка – положений планет по отношению к неподвижным звездам, погодных условий, солнечных гало, землетрясений, эпидемий, уровней воды и даже рыночных цен. Угловые расстояния определялись в «пальцах» и «локтях» (по 24 пальца в каждом); те же единицы использовались для измерения длины. В случаях, когда при интерпретации данных наблюдения можно было сопоставить локти с градусами, один локоть оказывался равным примерно 2,2 градуса, но при вычислениях обычно используют величину 2 градуса.
Собрания наблюдений доказали свое огромную значимость позднее спустя долгое время. В частности, александрийский астроном Птолемей выбрал год восшествия на трон Набонасара (747 г. до н. э.) как точку отсчета своего календаря, главным образом потому, что имевшиеся в его распоряжении давние наблюдения начинались именно с этого времени. Некоторые доступные сегодня данные по затмениям восходят к 731 г. до н. э. Они включают также лунные и солнечные затмения, распределенные по 18-летним периодам, наблюдения Юпитера (12-летние периоды), Венеры (8-летние периоды, их механизм рассмотрен выше) и другие данные, касающиеся Меркурия и Сатурна. С течением времени добавилась более детальная информация, например записи о соединениях с неподвижными звездами и удалениях от них. Регистрация периодичности движения планет также являлась нововведением; хотя она и была известна задолго до этого, но не фиксировалась в явном виде даже в текстах МУЛ.АПИН. Эти записи широко использовались как вспомогательное средство для прогнозирования – короткие периоды для приблизительных прикидок и более длительные периоды в том случае, если требовалась бо́льшая точность.
18-летний солнечный и лунный период имел огромное значение в позднейшей истории календаря. Вавилоняне открыли период, по истечении которого цикл затмений начинает воспроизводиться примерно в том же порядке не только по характеру прохождения, но и по времени суток. Они обнаружили, что это случается каждые 18 лет или, точнее, 6585⅓ суток (18,03 года), образующие целое число (223) синодических месяцев (от новолуния до новолуния). Им повезло с этим открытием, поскольку, используя современную техническую терминологию, время суток, когда случается затмение, существенным образом зависит от движения Луны «в аномалии». Аномалистический месяц отсчитывается от перигея до перигея (перигей – ближайшая к Земле точка лунной орбиты), и получается, что 223 синодических месяца приблизительно равны 239 аномалистическим месяцам.
Сейчас самое время ввести представление о драконическом месяце, который измеряется относительно узлов лунной орбиты – точек на небе, где пути Солнца и Луны пересекаются. Если принять во внимание причины обоих видов затмений, становится очевидным, что для наступления затмения Солнце и Луна должны одновременно находиться вблизи узлов. (Луна может отклоняться от солнечной траектории примерно на пять градусов, а видимые угловые размеры обоих объектов составляют только около половины градуса. Угловые размеры земной тени на расстоянии лунной орбиты, в которую Луна вступает во время лунного затмения, – около 84′.) Здесь опять 223 синодических месяца равны примерно 242 драконическим месяцам, и это целочисленное совпадение является условием столь хорошего соответствия 18-летнего периода для расчета затмений.
Некоторые современные авторы до сих пор ошибочно называют период из 223 месяцев саросом, используя греческое слово, когда-то обозначавшее гораздо более долгий вавилонский период времени (3600 лет). Современное использование этого слова имеет долгую и путаную историю; оно появилось не ранее чем в X в. н. э. и известно нам по энциклопедии Суда. Сами древние греки иногда, чтобы избавиться от разницы в ⅓ дня, брали период из 669 месяцев, так называемый экселигмос. Он также был известен ранее вавилонянам.
223‐месячный период, как иногда полагают, использовался главным образом для приведения в соответствие солнечного и лунного календарей, однако его астрономическая ценность, очевидно, заключалась не только в этом. В долгосрочной перспективе он мог помочь отыскать фундаментальные астрономические периоды, относящиеся к движению Солнца и Луны, от которых так сильно зависит точная теория планетных движений. Тем не менее самые первые попытки использования 223‐месячного периода связаны с определением дат возможных затмений, без какой-либо гарантии наступления затмения в действительности. Вероятнее всего, он сначала использовался для лунных затмений, и лишь спустя какое-то время – для солнечных. Согласно открытию вавилонян, затмения должны происходить через каждые 6 месяцев, но иногда случаются через пять. Предположим, что в одном 223‐месячном периоде содержится x 6‐месячных интервалов и y 5‐месячных. Тогда 6x + 5y = 223. Это уравнение имеет единственное решение, в котором x равен 33, а y – 5. Табличные схемы с датами возможных лунных затмений, включающие в себя эти числа, составлены вавилонянами не позднее 575 г. до н. э., но самые ранние известные нам описания затмений были начаты в 747 г. до н. э., и они уже содержали предсказанные затмения. В более поздние периоды существовали предсказания затмений с указанием времени дня или ночи, когда, предположительно, должно начаться затмение.
Желающие оценить точность упомянутых выше соотношений, связанных с 223‐месячным периодом, могут использовать указанные современные значения для продолжительностей трех типов месяцев, а именно – синодического (29,5306 суток), аномалистического (27,5546 суток) и драконического (27,2122 суток). Для справки на будущее, есть еще один, четвертый тип месяца – сидерический, определяемый как период обращения Луны относительно звезд при наблюдении с Земли; он имеет численное значение 27,3217 суток. (Все сутки считаются сутками солнечного года.) Однако рассматривая 223‐месячный период с современной точки зрения и принимая во внимание то, что ни одно периодическое соотношение такого рода не может быть точным, мы упускаем из виду следующее: схема, воспроизводящая себя через целое количество дней, относилась к области желаемого, но не действительного. Оперирование округленными значениями также замалчивает тот факт, что отдельные месяцы немного различаются по продолжительности, в результате чего реальная длина 223‐месячных периодов превышает целое количество дней на небольшую переменную величину (колеблющуюся между 6 и 9 часами). Существуют две известные нам вавилонские схемы моделирования продолжительности 223‐месячного периода, свидетельствующие о выдающихся достижениях тех, кто занимался их разработкой.
По сравнению с этими открытиями, отыскание периодичностей, требуемых для лунно-солнечного календаря (объединяющего месяцы в годы), должно представляться относительно тривиальной задачей, и тем не менее она была одной из тех, которые относились к вопросам высочайшей важности во всех ближневосточных религиях, в Древней Греции, а затем – в исламском и христианском мирах. Ко времени VI в. до н. э. вавилоняне использовали 8-летний период (99 синодических месяцев), а затем 27-летний период (334 месяца), но гораздо чаще употреблялся период, устанавливающий равенство между 19 годами и 235 месяцами. Безукоризненность этого соотношения может быть легко проверена с помощью приближенного значения продолжительности синодического месяца, приведенного выше, однако, совершая проверку, мы можем легко упустить один очень важный момент. Что в данном случае мы должны выбрать в качестве продолжительности года?
Если взять 365,25 суток, то расхождение составит около 0,06 суток. Число 365,25, как мы знаем, само является приближенным, и тут мы снова должны учитывать различие между двумя способами определения единицы времени, в данном случае – солнечного года. По аналогии с лунным месяцем можно ввести понятие сидерического года, измеряемого по движению Солнца относительно неподвижных звезд. Согласно наиболее общеупотребительному астрономическому определению, по крайней мере после греков, год измеряется иначе (тропический год) – по повторяющемуся прохождению Солнца через точки равноденствий или солнцестояний. Сегодня отсчет обычно производится от момента прохождения Солнцем весеннего равноденствия – в высшей степени абстрактной точки, которая позже стала использоваться в качестве точки отсчета в астрономической системе координат – точки весны (или «Головы Овна»). Она образуется пересечением эклиптики и небесного экватора, и в день весеннего равноденствия Солнце проходит через эту точку при движении с юга на север.
Почему указанные два способа определения года дают неодинаковый результат? Причина этого была обнаружена и убедительно объяснена только во II в. до н. э. греческим астрономом Гиппархом. Рассматривая вопрос в долгой перспективе, можно сказать, что это расхождение является следствием непостоянства ориентации земной оси в пространстве. В результате точка весны – точка отсчета, задаваемая положением земной оси, – перемещается на фоне звезд. Поэтому продолжительность года, рассматриваемая как интервал между повторными прохождениями Солнца через точку весны – то есть тропический год – отличается от сидерического года. Первый насчитывает (сегодня) 365,2422 солнечных суток, а сидерический год – 365,2564 солнечных суток.
Разница крайне мала, но вавилонская астрономия была очень точной, и несколько циклических соотношений, упоминаемых вавилонянами, дают возможность убедиться в том, что они получены с использованием сидерического года. Поскольку древнегреческие астрономы обычно пользовались тропическим годом, мы имеем здесь дело с одним из нескольких фундаментальных расхождений в подходах, применяемых указанными двумя влиятельными группами астрономов.
Если это справедливо для Солнца и Луны, то в равной степени справедливо и для планет: существуют простые периодические соотношения, найденные вавилонянами задолго до нашей эры. Мы уже видели на примере Венеры: за 5 циклов изменения своего положения на небе относительно Солнца (на это у нее уходит ровно 8 лет) она снова возвращается в исходное положение относительно звезд. Вводя обозначение [5ц, 8в, 8л], мы можем утверждать, что некоторые из соотношений такого типа (во всяком случае, перечисленные ниже) использовались задолго до того, как их письменно зафиксировали при Селевкидах: для Меркурия это [145ц, 46в, 46л], для Марса [37ц, 42в, 79л] и [22ц, 25в, 47л], для Юпитера [76ц, 7в, 83л] и [65ц, 6в, 71л], наконец, для Сатурна [57ц, 2в, 59л]. То, как использовались эти периоды, объясняется в текстах особого типа, названных Заксом «целевыми-годовыми текстами».
Указанные соотношения не точны, и знавшие об этом вавилоняне использовали вспомогательные правила для их корректировки. Например, Венера после пяти обращений вокруг Солнца отстает в своем восьмилетнем цикле движения относительно звезд на 2½ градуса. Соображения такого рода вели к установлению более длительных периодических зависимостей. Если говорить о Венере, то поскольку ее отставание составляет 1/144 часть окружности, то через 720 циклов изменения своего положения на небе относительно Солнца (720 = 144 × 5) она совершит также целое число полных оборотов, и это составит 1151 солнечный год (8 × 144 – 1).
Кроме того, имелись аналогичным образом полученные долгопериодические зависимости для других планет; результатом особого тщания, с которым рассчитывались эти длительные периоды, стало появление, по сути, самостоятельного астрономического раздела, нашедшего широкое применение от Индии на востоке до (в более скромной форме) Греции на западе. Согласно одному преданию (рассказанному римским философом Сенекой), вавилонянин Беросс – жрец бога Бела и основатель астрономической школы на греческом острове Кос (III в. до н. э.) учил, что когда все планеты выстроятся в соединении в последнем градусе Рака, то наступит сначала мировой пожар, а затем – всемирный потоп. Здесь мы тоже наблюдаем своего рода идею периодичности. С учетом выяснившегося характера периодичностей, повторение планетных влияний легко становится частью религиозной и астрологической догмы и хорошо сочетается с представлением, будто вся история вообще и даже само человеческое бытие есть не что иное, как периодический феномен. Нужно сделать только одно – найти интервал времени, после которого история повторяется, то есть отыскать наименьшее общее кратное всех долгих планетных периодов. Для получения простого ответа задача была слишком трудна. В отдельных вариантах предания о жреце бога Бела указывалось число лет с большим количеством нулей, например 2 160 000 (600 × 3600). Введенный гораздо позже индуистский временной период под названием махаюга является всего лишь удвоенным значением указанного числа, а это ясно демонстрирует его связь с вавилонским времяисчислением. Когда греки предложили свою идею «Великого года», они тоже, как правило, предлагали большие числа, кратные 360.
Число 360, известное нам как количество градусов в окружности, является своего рода фирменным знаком Вавилона. К началу V в. до н. э. у вавилонян уже существовали задатки координатной системы, поскольку они начали делить зодиак на двенадцать «знаков» одинаковой длины, называя их именами созвездий или значимых групп звезд – Овен, Телец (или Плеяды), Близнецы, Рак и т. д. Однако и тогда, и в более поздние времена существовал риск перепутать знаки с созвездиями из‐за сходства их названий. Со временем вероятность ошибки еще более возросла, поскольку прецессионное смещение полностью вывело звезды за пределы их первоначальных зодиакальных знаков. По этой причине вавилонская система координат, задаваемая относительно отдельных звезд, а не точки весны, была далека от совершенства, хотя их выбор понятен: звезды вполне наблюдаемы, а точка весны – нет.
Эти системы отличались друг от друга, но хорошей иллюстрацией того, что эти отличия часто не принимались во внимание, является общее для всех вавилонян утверждение, согласно которому точка весны находится в 8˚ Овна. Это замечание просочилось во второразрядную средневековую астрономию, а когда утратился контекст его употребления, оно окончательно потеряло всякий смысл. (Позже оно приобрело новое значение в контексте теории приливов и отливов, к чему мы вернемся в главе 8.)
Первый греческий текст, где использовались градусные астрономические обозначения, написал Гипсикл в середине II в. до н. э. (Более ранние авторы определяли угол в долях окружности или квадранта.) Вавилонские градусы ввел в употребление Гиппарх, самый влиятельный астроном до Птолемея. Однако Страбон, живший столетием позже, утверждает, что Эратосфен пользовался делением окружности на шестьдесят равных частей.
ВАВИЛОНСКАЯ АСТРОНОМИЯ В ПЕРИОД СЕЛЕВКИДОВ
Введение системы небесных координат – в данном случае деление зодиака на двенадцать знаков по тридцать градусов в каждом – имело громадное значение для развития математической астрономии. Точные планетные периоды могли быть получены и без нее – из наблюдений, осуществляемых в течение долгого времени, однако такая система имела существенное значение для анализа нюансов планетного движения. Мотивы проведения такого анализа должны были быть в той или иной мере рациональными, хотя они имели много общего с религией и астрологическими предсказаниями.
Древняя месопотамская звездная религия поощряла только примитивную астрологию простых предзнаменований. В других ближневосточных религиях, таких как орфизм и митраизм, поддерживалась чуть более развитая зодиакальная астрология, и с расширением Персидской империи некоторые из этих верований получили распространение в римской и греческой цивилизациях. Из всех восточных религий зороастризм заслуживает того, чтобы сказать о нем подробнее. Эта религиозная доктрина, приписываемая пророку Зороастре (или Заратустре), постепенно стала господствующей религией в Иране, и по сей день имеются изолированные общины, практикующие ее в этой стране и в Индии. Доктрина основана на моральном дуализме добрых и злых начал и имеет много общего с древнейшими вавилонскими мифами, например с мифом о противостоянии Мардука и Тиамат. Однако ее отношение к астрономии менее очевидно. В своих поздних версиях она способствовала распространению учения о том, что естественное место человеческой души – на небесах, или, точнее, принимая во внимание западные трактовки, на планетных сферах. Были те, кто говорил о связи между зороастрийскими верованиями и ростом числа гороскопов рождения, особенно в Греции. Существовало убеждение: когда душа нисходит с небес (где она жила в согласии с вращением звезд), чтобы вселиться в человеческое тело, она продолжает подчиняться звездам. (Подобные рассуждения можно найти, например, в диалоге «Федр» афинского философа Платона.) Такая философская идея не может исчерпывающе объяснить феноменальный расцвет астрологии в поздний эллинистический период, но как бы то ни было, сам расцвет представляется вполне реальным, а это существенно увеличило спрос на астрономические предсказания. Греки прослышали о Зороастре в V в. до н. э., за столетие до Платона, однако будет небезынтересно узнать, что человеком, в значительной степени ответственным за распространение в Греции зороастрийских философских идей, являлся один из величайших греческих астрономов, живший в одно время с Платоном. Речь идет об Евдоксе Книдском – об этом ученом мы подробнее поговорим в следующей главе.
Каково бы ни было философское влияние зороастризма, его астрономическое содержание довольно наивно. Существовало определенное число рутинных процедур, в ходе которых использовалось астрономическое знание, например предсказание того, каким будет урожай, по утреннему восходу Луны после первого появления Сириуса; однако нет никаких оснований полагать, что персы всерьез верили в саму предсказуемость подобного рода вещей. И даже само астрологическое учение, по всей видимости, оказалось заимствованным. Математическая астрономия, необходимая для практики составления гороскопов, была практически полностью вавилонской. Старейший из известных клинописных гороскопов датируется 410 г. до н. э. Его нашли в одном из вавилонских храмов. В век Платона греки уже отдавали должное «магам» или халдеям, и в течение всей классической Античности эти слова употреблялись как синонимы слова «астролог». Тем не менее этот факт не должен (как это часто делалось в прошлом) отрицать блестящие математические достижения вавилонян, легшие в основу греческой астрологии.
Сохранилось более трехсот клинописных табличек этого типа. Многие из них повреждены, другие разбиты на фрагменты, хранящиеся раздельно в музеях разных стран. Сегодня их принято делить на «процедурные тексты» (в которых содержится разъяснение методов расчета) и «эфемериды» (где приведены результаты вычислений для заданного периода времени, подобно тому как это делается в современном «Морском астрономическом ежегоднике»). Количественно эфемериды (в переводе с греческого это слово означает просто «годный на день») в три раза превышают процедурные тексты. Все они были найдены в Вавилоне (при раскопках в 1870–1890 гг.) и Уруке (при раскопках в 1910–1914 гг.), так что даже сегодня мы можем не до конца отдавать себе отчет в том, каковы все достижения этих людей.
Стремление решить проблему Луны, вполне возможно, привело к обнаружению аналогичных решений для планет. Сколько дней в одном месяце? Вавилонский месяц начинался с первого появления тонкого лунного серпа после захода Солнца. Отсчет дней велся также, начиная с вечера. При таком способе определения месяц содержал целое количество дней и, как показывает опыт, их число равно либо 29, либо 30. Но какому из них отдать предпочтение? Сегодня у нас есть общая картина явления – модель, в отношении которой мы можем применить стандартные геометрические процедуры и получить ответ. И даже сегодня это не так уж просто сделать. Не имея предшественников, способных снабдить их такой моделью, вавилоняне должны были действовать в обратном порядке. Для начала попробуем оценить наиболее очевидные трудности, с которыми они столкнулись, путем демонстрации того, как мы сами могли бы провести подобный анализ сегодня.
Начнем с грубого оценочного предположения, что продолжительность месяца равна в точности 30 дням. Солнце движется по зодиаку со скоростью примерно 1˚ в сутки, поэтому от одного до другого соединения с Луной оно пройдет 30˚. Если считать по соединениям, то более быстро движущаяся Луна должна будет пройти 390˚, то есть двигаться со скоростью 13˚ в сутки в течение 30-дневного периода. (Более точное среднее значение этого числа составляет 13,176˚, но скорость Луны может заметно меняться.) Однако для предсказания времени первого появления лунного серпа необходимо принять во внимание несколько факторов:
1. Поскольку Солнце обладает высокой яркостью, то два светила должны находиться на заданном минимальном расстоянии друг от друга, иначе лунный серп будет неразличим.
2. Время, за которое Луна преодолеет это расстояние, зависит от относительной скорости Луны и Солнца. Среднее значение относительной скорости равно примерно 12˚ в сутки, однако эта «суточная элонгация» может варьироваться в пределах двух-трех градусов в ту или другую сторону.
3. Критическое расстояние зависит от яркости фона неба, а она в свою очередь зависит от угла между горизонтом и линией, соединяющей заходящее Солнце и лунный серп (см. ил. 31). Это, в свою очередь, определяется несколькими факторами: а) временем года, которое есть не что иное, как другой способ определения положения Солнца на «эклиптике» – годовом пути Солнца, проходящем через середину пояса зодиака; b) отклонением Луны от этого пути, ее «эклиптической широтой», достигающей 5˚; и c) географическим положением наблюдателя (широтой), определяющей углы пересечения звездами горизонта при восходе и заходе.
Вот, вкратце, описание процедуры, которой мы, вероятно, должны следовать. Самое удивительное заключается в том, что вавилоняне умели каким-то образом определять многие факторы, анализируя свои наблюдения в начале месяца. Они проделывали это, используя только арифметические методы, то есть не прибегая к геометрическим моделям, и если мы воспроизводим здесь их результаты в графической форме, то только потому, что это экономит нам время. (Для получения полного представления о том, как это делалось на самом деле, нужно познакомиться с работой Отто Нейгебауера «Astronomical Cuneiform Texts», где содержится соответствующий расшифрованный и проанализированный материал.)

31
Первое наблюдение лунного серпа. Солнце находится ниже западного горизонта, линия его спуска не показана. (Она не совпадает с эклиптикой и определяется вращением неба вокруг Полюса мира.) Луна может находиться в пределах чуть более 5° в ту или другую сторону от эклиптики.
Известны две основные системы, посредством которых осуществлялось представление различных солнечных, лунных и планетных движений. В первой, называемой «Системой А», предполагалось, что на достаточно большом участке зодиака скорость (например, Солнца) остается постоянной величиной с каким-либо определенным значением, затем происходит изменение значения, и оно снова считается постоянным в течение достаточно продолжительного промежутка времени до момента следующего изменения и т. д. Возникает потребность в правилах перехода. Если представить зависимость скорости от времени графически, то получим кривую, напоминающую по внешнему виду зубчатую стену крепости с бойницами (в общем случае – нерегулярную), которую часто называют «зигзагообразной функцией». «Система Б», на первый взгляд, выглядит более сложно. В ней предполагается, что каждая строка в таблице положений (или чего-либо другого) отличается от предыдущей, но разница образует постоянное положительное либо отрицательное число, исключая те случаи, когда возникает значение, заведомо выходящее за пределы максимума или минимума. Если это случается, направление изменений (увеличение или уменьшение) меняется на противоположное. Если мы построим график по этой таблице значений, он будет иметь неровную пилообразную форму зигзагообразной функции. Система А, как было установлено на практике, является более гибкой, поскольку может быть легко использована с любым количеством шагов различной длины, а это делает ее более точной по сравнению с жесткой конфигурацией Системы Б.
Перемена направлений в зигзагообразных функциях производится в соответствии со строгими правилами, которые легче всего объяснить с помощью ил. 32. На этом рисунке изображен график, построенный по эфемеридам, составленным на 179 г. эры Селевкидов (133–132 гг. до н. э.). По горизонтальной шкале отложена последовательность месяцев (как они тогда понимались), их названия перечислены в первом столбце таблички. Они, как выяснилось, маркируют дни, когда происходило соединение Солнца с Луной. Вертикальная шкала соответствует второй колонке таблички, содержащей шестидесятеричные числа, равные по порядку величины 28 или 29. Следующая колонка таблицы, не отображенная на графике, может быть интерпретирована как перечисление долгот Солнца и Луны в моменты их соединений. Смысл чисел, записанных во второй колонке, стал понятен только после того, как их проанализировали современные ученые. Поскольку оказалось, что вторая колонка содержит разности между соседними записями в третьей колонке, она (вторая колонка), очевидно, должна содержать, как мы сказали бы сейчас, скорости Солнца (изменение долготы в течение месяца). Пользуясь графическим способом объяснения чисто арифметических величин, мы можем сказать: зигзаги, построенные с помощью прямых линий, возникли как аппроксимация вавилонянами определенного процесса, для отображения которого нам сегодня понадобилась бы по меньшей мере синусоида. И все же это было их выдающимся достижением.
Можно легко посчитать период зигзагообразной функции в месяцах. На ил. 32 он записан в виде числа 12;22,08,53,20. Это значение соответствует продолжительности года, измеряемой в синодических месяцах. Его получили, очевидно, не прямыми наблюдениями, а с помощью одного из циклических соотношений, о которых мы упоминали ранее. Похоже, в данном случае использовалось равенство: 810 лет = 10 019 месяцев. Конечно, для выведения этих уравнений необходимо было проводить наблюдения, но поиск правильных числовых соотношений также играл свою роль. К сожалению, нам известны только итоговые результаты этих расчетов.

32
Зигзагообразная функция вавилонян в современном графическом представлении.
Нашлись и другие характерные равенства, например 225 лет и 2783 месяца, где на один год приходится 12;22,08 месяцев. Это число обнаружено в табличках, составленных с использованием как Системы А, так и Системы Б. Одним из наиболее неожиданных открытий для тех, кто работал с этими клинописными табличками, стало то, что, хотя Система А была более древней, обе системы регулярно использовались в течение всего периода, к которому относятся сохранившиеся таблички (ок. 250–50 гг. до н. э.), как в Вавилоне, так и в Уруке.
Относительно редко встречающиеся лунные эфемериды охватывали периоды более одного года. Большинство из них содержали столбцы со скоростями и положениями Луны и Солнца. В некоторых указывалась продолжительность дней или ночей, согласующаяся с положением Солнца в предыдущем столбце. У нас есть возможность рассчитать это, используя методы сферической тригонометрии, но вавилоняне пользовались только арифметическими методами. Иногда встречаются колонки с широтами Луны, а иногда – колонки с максимальными фазами затмений. Алгоритм (принцип расчета) для определения максимальной фазы затмения применялся каждый месяц, вне зависимости от того, намечалось оно или нет. Это может быть расценено, с одной стороны, как нечто несовместимое с духом эмпирической науки, с другой, как свидетельство высокого уровня абстрагирования и ясного осознания понятия математической функции. В числе вспомогательных процедур можно упомянуть такие, как исправление результатов расчета скорости Солнца, она на первом этапе вычислений считалась постоянной, но о ее переменности было хорошо известно. Осуществление этих исправлений в Системе Б сопряжено с бо́льшим количеством трудностей, чем в Системе А, а это отчасти объясняет причину ее долгого использования.
Как уже пояснялось на с. 85, существовало ясное понимание того, что ни лунное, ни солнечное затмения невозможны в случае, если потенциально затмеваемый объект располагается в момент новолуния или полнолуния на слишком большой широте. Предсказание солнечных затмений гораздо более сложная проблема, чем предсказание лунных. По этому поводу можно только сказать, когда они не произойдут. Для их предсказания необходимо обладать гораздо большей информацией о расстояниях между Землей, Солнцем и Луной и их размерах. Не существует твердых доказательств того, что были известны закономерности повторяемости солнечных затмений (еще один способ их предсказания), хотя есть те, кто настаивает на обратном.
Упомянутые таблички содержали данные о долгих периодах солнечных и лунных движений, но имелись и другие, в которых с помощью аналогичных методов отмечались ежедневные изменения, и из них могло быть выведено, например, равенство: 251 синодический месяц = 269 аномалистических месяцев. В данном случае продолжительность синодического месяца получалась равной 29;31,50,08,20 суткам, а аномалистического – 27;33,20 суткам. Могут возникать сомнения по поводу высокой точности этих чисел, однако сегодня мы пользуемся практически идентичными значениями, отличающимися от приведенных на одну шестимиллионную и четыре шестимиллионных соответственно. (С того времени эти периоды изменились, хотя и на очень малую величину, так что приведенное сравнение нельзя считать абсолютно строгим, хотя это не умаляет его исключительных достоинств.) Еще более интересно провести историческое сравнение продолжительности указанного здесь вавилонского синодического месяца с месяцем, используемым в Европе эпохи Высокого Средневековья в так называемых Толедских таблицах. Эти параметры идентичны как по значению, так и по целям, хотя их разделяет более тысячи лет.
Когда в эпоху Селевкидов вавилоняне обратили свое внимание на планеты, их арифметические преобразования (используем еще раз нашу графическую аналогию) стали на шаг ближе к идеальной синусоиде. Кроме того, существовали таблички, которые задавали, если можно так выразиться, широ́ты Луны, и в них простые зигзагообразные линии были уже модифицированы, что приблизило их к идеальной синусоиде, как показано на ил. 33. Перед объяснением того, как действовали вавилоняне, будет полезно получить примерное представление о реальном движении планет и о том, как оно воспринимается земным наблюдателем. Поэтому следующее неисторическое отступление содержит изложение базовых сведений по вопросам, разбираемым в этой и следующих главах, в которых рассматриваются классические теории планетных движений.

33
Графическое представление решения вавилонянами того, что может быть обозначено как проблема лунной широты. (Здесь мы принимаем во внимание только общие принципы. Строго говоря, все это, скорее всего, делалось для получения вспомогательной функции, позволяющей осуществить предвычисление затмений, но базовая идея может быть выражена и в категориях определения долготы.)
ДВА ПОДХОДА К ИЗУЧЕНИЮ ПЛАНЕТНЫХ ДВИЖЕНИЙ: НЕИСТОРИЧЕСКОЕ ОТСТУПЛЕНИЕ
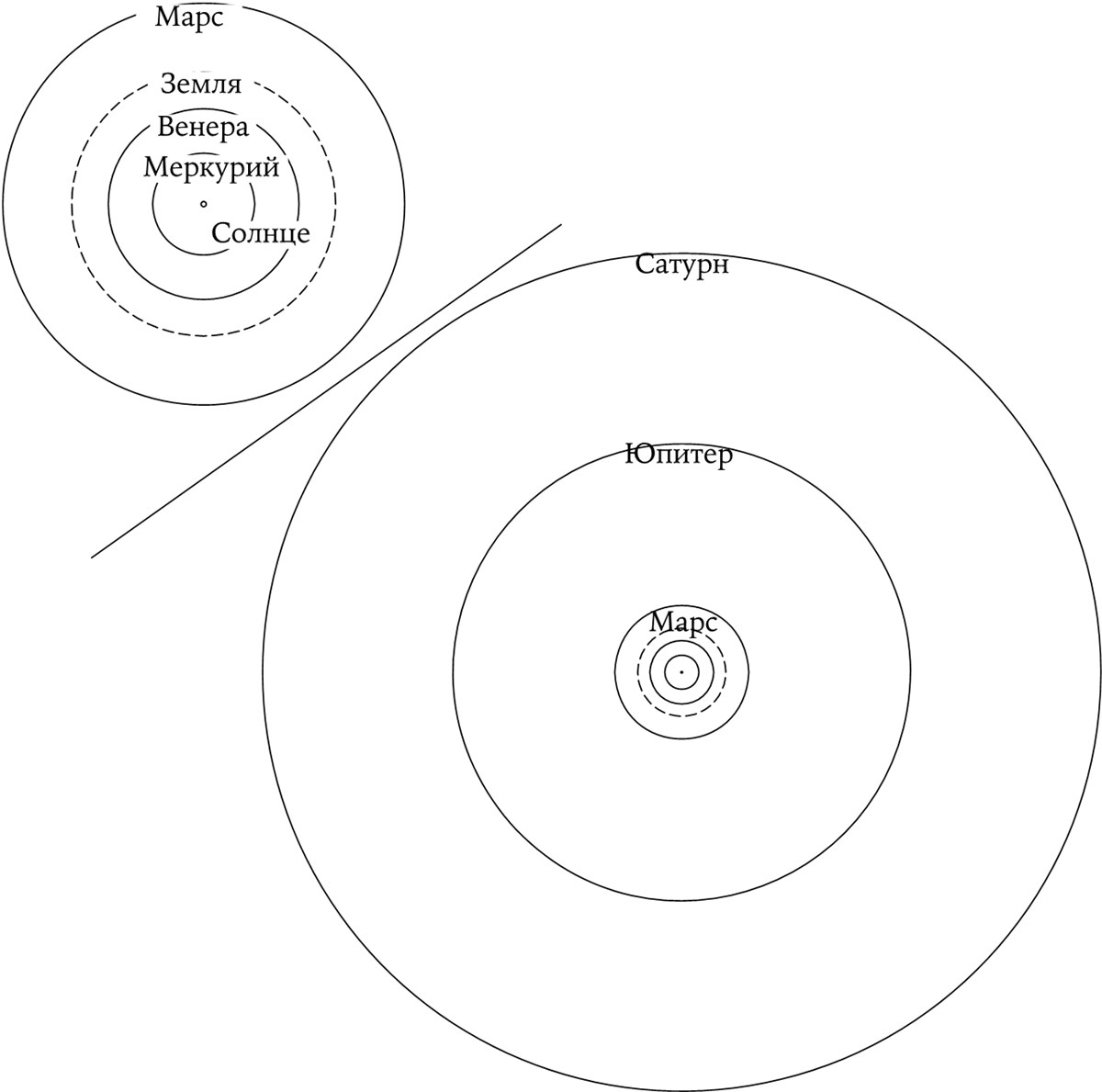
Все планеты, известные до XVIII в., движутся по своим орбитам вокруг Солнца. Меркурий – ближайшая к Солнцу планета, за ним следуют Венера и потом Земля. Орбиты Марса, Юпитера и Сатурна находятся за пределами земной орбиты (ил. 34). «Нижние» и «верхние» планеты (или «внутренние» и «внешние») несколько различаются по характеру своего движения при наблюдении с Земли. Как удалось показать Иоганну Кеплеру, каждая орбита представляет собой эллипс, в фокусе которого находится Солнце; однако в первом приближении все орбиты можно считать круговыми с одним общим центром, где располагается Солнце. Представим себе схематичное изображение этой системы с булавкой в точке, обозначающей Солнце. Если мы вытащим булавку и воткнем ее в точку, обозначающую Землю, то относительные положения планет останутся прежними, и нетрудно догадаться, что тогда мы можем рассматривать планеты обращающимися по окружностям, центр которых совпадает с движущимся Солнцем.
34
Предполагается, что орбиты планет – круговые. Размеры орбит на обоих рисунках изображены приблизительно в одном масштабе.
Рассмотрим простейший случай движения нижней планеты Меркурий. Теперь, как мы полагаем, она является спутником Солнца. Пользуясь традиционной терминологией, можно назвать круг, описываемый Солнцем, кругом дифферента (дословно – «несущий круг»), тогда орбита спутника – переносимый круг – будет эпициклом. Другая нижняя планета, Венера, будет двигаться по более широкому эпициклу. В случае верхних планет эпициклы и дифференты поменяются ролями, но у нас пока нет нужды вдаваться в эти подробности.
Описание индивидуального движения отдельных планет с помощью эпициклов имело громадное значение в истории астрономии, хотя необходимо подчеркнуть: каждая планета рассматривалась в отдельности, ее эпициклическое движение считалось полностью автономным, и пришлось пройти долгий и мучительный путь для понимания того, что Солнце наличествует в системе эпицикла и дифферента каждой планеты. Только после того как это было окончательно осознано Коперником, оказалось возможным объединить планеты в единую систему или, фигурально выражаясь, проткнуть одной булавкой все точки нахождения Солнца в каждой отдельно взятой системе.
Такой способ объяснения предоставляет богатые возможности для внесения уточнений; например, сообщая эпициклу небольшой наклон к плоскости солнечной орбиты, можно учесть факт расположения планет не всегда строго в этой плоскости, а потому они могут смещаться по широте. «Эклиптическая долгота» измеряется вдоль эклиптики с началом отсчета в месте пересечения эклиптики (солнечного пути) с экватором. Этим началом отсчета является точка весеннего равноденствия, о которой мы уже упоминали выше. «Эклиптической широтой» называется координата, измеряемая от эклиптики в направлении полюса – северного или южного.
Эпициклическое описание было типично для поздней греческой астрономии, но не для вавилонян. После того как выяснились его достоинства, решение астрономических задач значительно упростилось. Стратегия заключалась в том, чтобы подобрать подходящую геометрическую модель и получить из нее все необходимые следствия, например о последовательности восходов и заходов планет. После этого полученные теоретические следствия могли быть проверены с помощью наблюдений. Если модель оказывалась более или менее верной, то эти и последующие наблюдения давали астрономам возможность определить или уточнить численные характеристики модели, такие как параметры и относительные размеры кругов, угловые скорости при движении по кругам и времена, когда планеты проходили через особым образом заданные точки, от которых велся отсчет их движения. Вавилоняне, появившиеся на исторической сцене гораздо раньше, действовали в более или менее обратном порядке: то, что для греков (равно как и для нас) было выведенным следствием, для них являлось точкой отсчета – исходным фактом. Рассмотрим, например, как они оперировали с восходами и заходами на горизонте. Это очень естественно – обращать внимание на первое появление светил, и интерес к такого рода явлениям являлся общим для большинства ранних культур. Однако такие наблюдения предоставляли астрономам крайне скудную информацию, и факт получения на их основе далеко идущих теоретических обобщений можно считать настоящим чудом.
Мы уже упоминали о первом и последнем появлении звезды Сириус, которая значительную часть года бывает скрыта в солнечных лучах, а также о том, что планеты тоже могут быть невидимы какое-то время по тем же самым причинам. Нижние планеты – Меркурий и Венера – никогда не отходят от Солнца слишком далеко относительно своего положения в соединении и подчиняются моделям движения, вкратце упомянутым ранее (см. ил. 35 и приведенную выше ил. 29). Как и раньше, мы можем рассмотреть этот вопрос с современной точки зрения. Когда нижняя планета движется по той части своей орбиты, которая обозначена пунктиром, ее угловое расстояние от Солнца настолько мало, что она теряется в сиянии Солнца. В точке FM она становится впервые видимой, в данном случае в качестве утренней звезды. При наблюдении с Земли увлекаемая Солнцем планета будет ежедневно смещаться по небу. Тот факт, что она будет наблюдаться по утрам незадолго до восхода Солнца, с очевидностью следует из верхней части рисунка, где орбита изображена почти под ребром к наблюдателю. LM является точкой, в которой она последний раз будет наблюдаться в качестве утренней звезды, а FE и LE – точками первого и последнего появления планеты как вечерней звезды.

35
Утренние и вечерние восходы и заходы Меркурия и Венеры. Нетрудно изобразить аналогичную диаграмму для внешних планет, орбиты которых находятся за пределами орбиты Земли.
Когда мы имеем дело с нижними планетами, по определению находящимися недалеко от того же места на горизонте, где и Солнце, наше представление на основе четырех точек (FM, LM, FE, LE) является самоочевидным. Ведь как мы смогли убедиться, гелиакический восход в данном случае является первым наблюдаемым появлением светила на горизонте до восхода Солнца (FM), а гелиакический заход – последним наблюдаемым заходом светила сразу после заката (LE). Однако восходы Марса, Юпитера и Сатурна могут наблюдаться после того, как зайдет Солнце, а заходы – непосредственно перед рассветом, поэтому для того, чтобы начать рассуждение о них, нам нужно дополнить нашу классификацию такой категорией, как «первый утренний заход». Употребление понятий «акронический» (не путать с «ахроническим») и «космический», часто используемых для обозначения восходов и заходов в указанном выше смысле, бывает неочевидным при недостаточно внимательном отношении к описываемому явлению. Лучше не определять их вовсе, но при знакомстве с работами, где они употребляются, помнить, что первое прилагательное относится к регистрации вечернего события (не важно, первого или последнего), а второе – утреннего.

36
Спиральная траектория Меркурия относительно Земли. Солнце обращается вокруг Земли, как показано на рисунке, и орбита Меркурия, обращающегося вокруг Солнца, движется вместе с ним. Изображенная здесь спиральная кривая охватывает период 400 дней.
Допустим, Земля неподвижна, а Солнце обращается вокруг нее. На самом деле, как мы знаем, планеты обращаются вокруг Солнца, следовательно (если мы принимаем это допущение), движение планет будет казаться спиралевидным, как в немного измененном виде показано для Меркурия и Венеры на ил. 36 и 37. Планеты никогда не наблюдаются слишком далеко от плоскости движения Солнца относительно звезд (эклиптики). Как уже говорилось, именно вдоль этого видимого пути мы отсчитываем (небесную) долготу. Для альтернативного представления планетного движения, совершающегося в соответствии с нашими геометрическими схемами, мы можем просто составить таблицу зависимости их небесной долготы от времени или, что еще лучше, изобразить ее в виде графика. На ил. 38 приводится вид этой зависимости для Меркурия, где по горизонтальной оси отложена шкала времени длиной примерно в один год, а по вертикальной – долгота Меркурия, отсчитываемая от точки весеннего равноденствия. Изображена и долгота Солнца: это диагональ, проходящая через середину кривой Меркурия, – линия, относительно которой Меркурий как бы осциллирует. За год Меркурий совершает вокруг Солнца около четырех оборотов. (Сидерический период его обращения равен 0,24 тропического года.) На графике отмечены точки первой и последней видимости (в соответствии с обозначениями, приведенными в предыдущем абзаце) и так называемые планетные стояния, в которых планеты кажутся неподвижными на фоне звезд, то есть когда их прямое движение меняется на попятное (S1) и наоборот (S2).
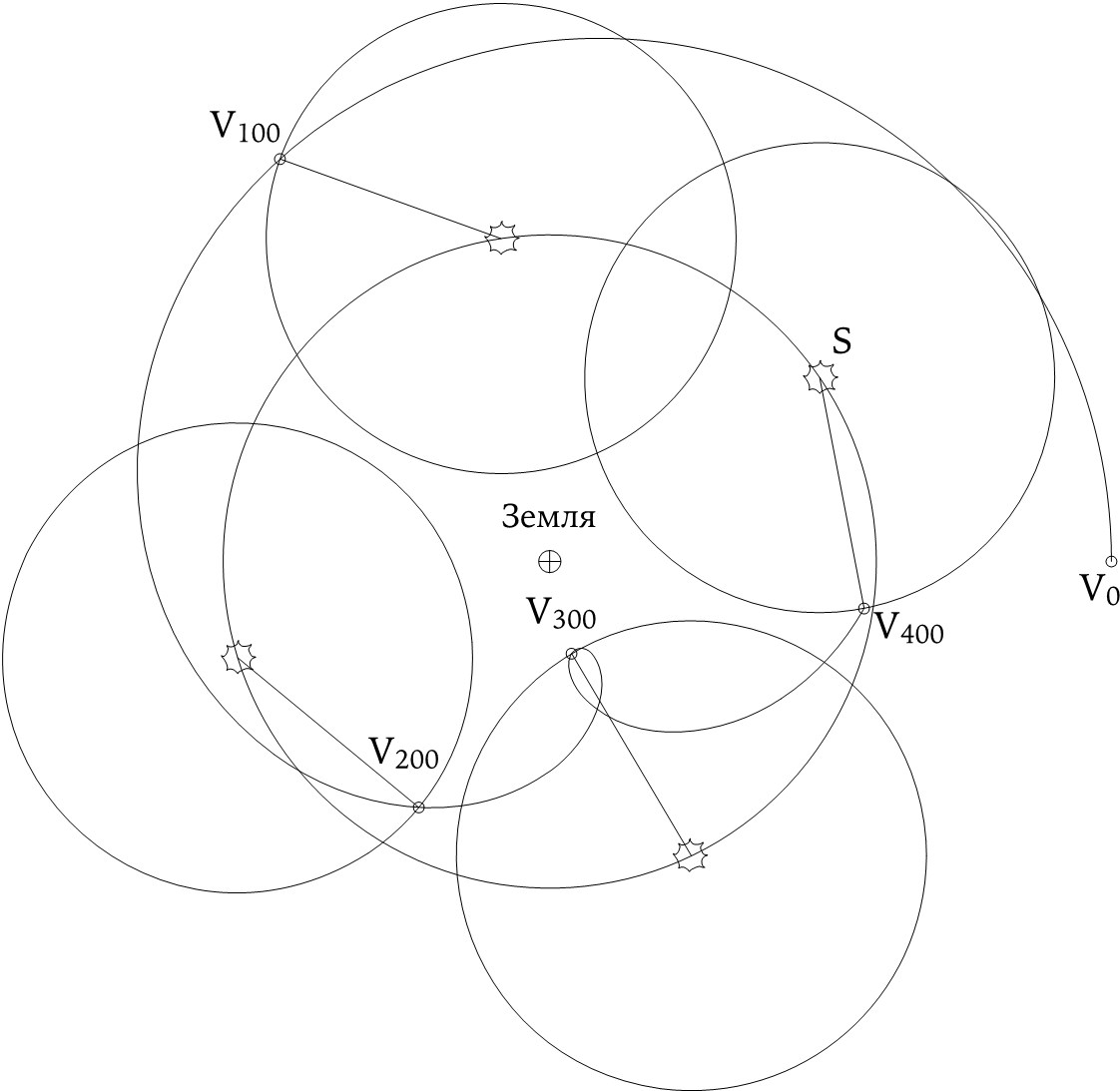
37
Спиральная траектория Венеры (V) относительно Земли. Диаграмма в целом похожа на изображенную на ил. 36, однако теперь Солнце (S) и соответствующие положения планетной орбиты изображены с интервалом в 100 дней, что вместе образует 400 дней. Как и прежде, в качестве начальной точки мы выбираем положение, когда Солнце находится на линии, соединяющей Венеру с Землей. (Эта ситуация не типична. Приблизительная симметрия относительно 100-дневного интервала – не правило, а случайное стечение обстоятельств.)

38
График изменения долгот Меркурия и Солнца примерно за один год. Используемые обозначения (FM, LM и т. д.) приводятся в соответствии с тем, как они определены выше в настоящей главе.
Характер движения верхних планет может быть проиллюстрирован на примере Марса (ил. 39 и 40). В данном случае декартов график охватывает период более шести лет, и так как вертикальная ось отображает долготу – координату сугубо циклическую, – то линии, соответствующие как Солнцу (правильные прямые), так и Марсу, должны периодически обрываться. Здесь также можно выделить несколько очевидных общих принципов. Близость к Солнцу, делающая планету труднодоступной для наблюдения, наступает в середине продолжительного периода достаточно ровного прямого движения, в то время как в период попятного движения планета находится в противостоянии (на расстоянии 180° от Солнца по долготе). Линии, соответствующие Солнцу, очевидно, распределены по годовым интервалам, и это распределение со всей определенностью свидетельствует о том, что изгибы кривой Марса отстоят друг от друга чуть меньше, чем на два года. На деле, сидерический период Марса равен 1,88 тропического года. Также приблизительная оценка этой периодичности может быть получена из ил. 39, где спираль, отображающая движение Марса за период более чем 700 дней, возвращает планету почти в точности в ту же точку, из которой она вышла.

39
Спиральная траектория Марса относительно Земли согласно модели, имеющей много общего с применявшейся для нижних планет. Нарисованные положения планеты разделены 100-дневными интервалами. Показано, что планета возвращается в исходную точку примерно через два года. Приведенная здесь диаграмма предваряет более содержательное обсуждение эпициклических моделей в главе 4. Их связь с современными представлениями о Солнечной системе (даже в упрощенной первоначальной форме) затруднена отсутствием на рисунке в явном виде точек, соответствующих положению Солнца, вокруг которого обращается Марс. Однако связь с Солнцем может быть установлена по радиусам эпициклов, отмечающим положение Марса в эпицикле. Эти радиусы, как видно, постепенно меняют свое направление. Причем это происходит таким образом, что полный цикл завершается за один год, аналогично тому, как это происходит с пространственной линией, соединяющей Землю и Солнце.

40
Изменение долготы Марса (извилистые линии) и Солнца за период 2400 дней (сравните с приведенными выше графиками Меркурия и Солнца). Эти графики представляют собой всего лишь регистрацию наблюденных положений планеты по долготе. Задача астронома заключается в том, чтобы объяснить их.
ВАВИЛОНСКАЯ ПЛАНЕТНАЯ ТЕОРИЯ
Мы уже видели, насколько важен был интерес к горизонтным событиям для выработки общих правил, легших в основу таблиц с материалами наблюдений Венеры времен Амми-цадуки. Интересно заметить, что, когда вавилоняне анализировали особенности первого и последнего, а также вечернего и утреннего появлений, они рассматривали их как не связанные друг с другом явления. Как будто бы каждый из этих объектов обладал собственным существованием, располагаясь на эклиптике. Рассмотрим, например, точки, обозначенные на графике Меркурия как FM (см. ил. 38 выше). Если взять большое количество таких точек и рассмотреть их независимо от прочих, то они образуют более или менее прямую линию, параллельную графику движения Солнца, но эта линия не будет идеально ровной. Для расчета отклонения от этого (в нашем представлении) прямолинейного графика вавилоняне использовали ту же арифметическую методику, которую они применяли в отношении Солнца и Луны. Если использовать графический подход, то суть проблемы заключается в том, чтобы разбить получившуюся линию на сегменты, или, другими словами, найти точки разрыва и градиенты соответствующих компонентов. Вавилоняне, похоже, выражали эти градиенты (угловые скорости) посредством отношения целых чисел и делали это следующим образом: «Меркурий совершает 1513 явлений за 480 лет». Или, ссылаясь на вторичный, более понятный нам результат: «Меркурий восходит 2673 раза за 848 лет».
Найти такие соотношения не так-то просто, и то, что вавилоняне были связаны по рукам и ногам лунным календарем, еще более осложняло ситуацию, поскольку планетные периоды, безусловно, не имели ничего общего с движением Луны. Тем не менее это не имело такого уж большого значения, поскольку, хотя они и не выражали даты в сутках, применялась другая единица – одна тридцатая часть среднего синодического месяца. Сегодня ее обычно называют титхи (слово, пришедшее из поздней индуистской астрономии, где использовалась та же единица). По продолжительности титхи очень близки к суткам. Лунное движение замысловатым образом варьируется, но поскольку титхи по определению являются средней величиной, они, в принципе, вполне могут быть использованы в хорошо разработанной астрономической системе. Нельзя сказать, что эта единица была оптимальным выбором с точки зрения астрономии, однако она обладала очевидными преимуществами для тех, чья религия требовала обращения к древнему лунно-солнечному календарю.
Помимо совокупности правил, характеризующих явления типа FM, были найдены аналогичные правила для явлений LM, FE и LE. Общий принцип заключался в нахождении величин (долгот и времен, измеряемых в титхи), прибавляемых к исходным данным (для FM) для получения последующих явлений. Итоговый график, посредством которого мы можем воспроизвести эти арифметические преобразования, является вполне приемлемой аппроксимацией синусоидальной формы приведенных выше графиков.
Одним из наиболее изощренных элементов этих упражнений стало внесение в вычислительные схемы определенных «феноменов», на деле не поддававшихся наблюдению. Лучшей аналогией, объясняющей эту ситуацию, по всей видимости, является пример с полнолуниями. Точный момент этого явления наступает большей частью тогда, когда Луна находится под горизонтом, но расчеты предсказывали его вне зависимости от того, была она видна или нет. Другие, уже рассмотренные нами, «феномены» (FM, LM, FE и LE) аналогичным образом исходно возникали благодаря наблюдаемым событиям, а затем постепенно превращались в вычислительные абстракции, так сказать, идеальные точки на нашем идеальном графике.
Впоследствии во многом похожие процедуры применялись ко всем планетам, хотя в данном случае теоретические разработки оказались не столь впечатляющими. Общей целью являлось вычисление долгот и дат основных планетных явлений. Для верхних планет: первое появление после периода невидимости и исчезновение; противостояние; два стояния, когда планета останавливается перед тем, как сменить направление движения. Большинство сохранившихся данных относится к Юпитеру. Таблички Марса из Урука замечательны тем, что они довольно точно отражают весьма сильно меняющуюся скорость этой планеты. Для внутренних планет появления и исчезновения подразделялись на происходящие в западной части неба и происходящие на востоке. В случае Венеры учитывались еще и стояния. (У Меркурия они очень трудно наблюдаемы.) В табличках из Вавилона и Урука представлены все известные к тому времени планеты. Невозможно с точностью сказать, какой из этих двух городов дал начало рассмотренным методам и когда их применили впервые, однако Систему A, скорее всего, разработали за пятьдесят лет до или пятьдесят лет после начала IV в. до н. э., а Систему Б – чуть позже. В обоих городах были в ходу несколько различных методик арифметического представления, и такая ситуация сохранялась по меньшей мере до I в. н. э. Сказать о том, что общие идеи методов являлись всегда одинаковыми, равносильно заявлению, будто все самолеты летают по одной и той же траектории. В рамках данной работы невозможно подробно изложить особенности каждого из методов. Однако сохранилось несколько табличек, и это необходимо отметить, в которых «точки графика», являющиеся промежуточными по отношению к ключевым событиям (FM, FE, первое стояние и т. д.), дополнялись промежуточными точками. Эти точки определялись непрямой интерполяцией (непрямолинейными сегментами, если использовать нашу графическую интерпретацию), а посредством методов, основанных на определении разностей второго и даже третьего порядка. Есть науки, до сего дня не достигшие такого уровня сложности.