1.2. Простые проценты
При использовании простых ставок процентов сумма процентов определяется исходя из первоначальной суммы или базы. Схема простых процентов предполагает неизменность базы, с которой происходит начисление процентов.

Рассмотрим на примере, как выводится формула расчета наращенной суммы, используя принцип простых процентов.
Клиент приходит в Банк, чтобы выбрать самый доходный вклад на 3 года, сумма его ограничена 100 рублей. Банк предлагает ему 2 вклада под 10% годовых, с начисление простых и сложных процентов. Клиент ничего не понимает в финансовых расчетах, и сотрудник банка решает ему объяснить схему начисления простых процентов.

По итогам первого года сумма вклада с процентами будет составлять 110 рублей, исходя из первоначальной суммы вклада и начисленных процентов.
К концу второго года сумма вклада будет увеличена на сумму процентов за этот год, т.е. на 10 рублей.
На момент закрытия вклада сумма с процентами будет составлять уже 130 рублей, т.к. за третий год также будут начислены проценты от первоначальной суммы вклада.
Если упростить данный расчет, то он будет выглядеть следующим образом.

Если вместо цифр поставить соответствующие обозначения, получается следующая формула:

Разберем для закрепления небольшой пример.
Ростовщик выдал клиенту 300 рублей, через 6 месяцев клиент отдал ему 336 рублей. Необходимо узнать, какова была процентная ставка в месяц по данной сделке?
Итак, у нас есть формула начисления простых процентов
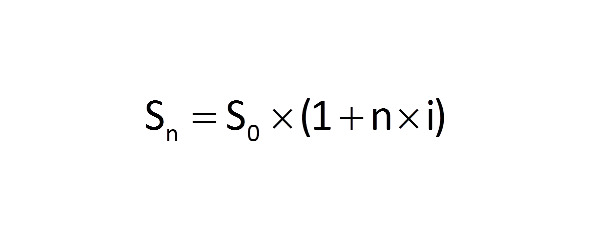
Что нам известно? Известно, что итоговая сумма составила 336 рублей, начальная сумма составляла 300 рублей, период составил 6 месяцев. Необходимо найти неизвестное i в данной формуле, используя простейшие математические расчеты.
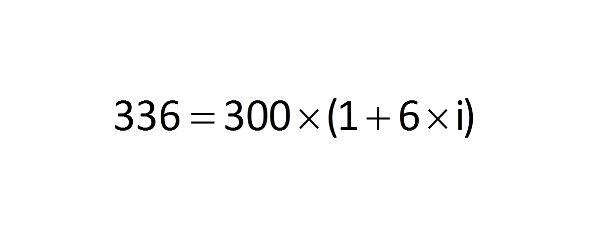
Таким образом, процентная ставка в месяц составила в данном примере 2%.
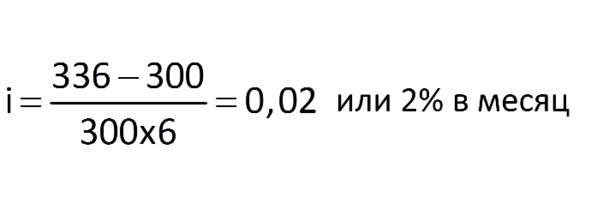
Если представить этот расчет в уже знакомых нам обозначениях, то он будет выглядеть так:
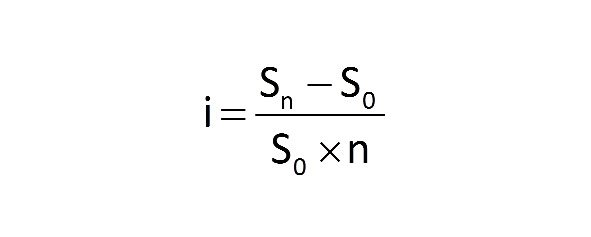
Данную формулу можно применять для различных расчетов. Например, находит начальную сумму, если известны прочие данные уравнения.