Все науки. №7, 2022. Международный научный журнал - читать онлайн

УДК 519.9

Нематов Ислом

Кандидат физико-математических наук, доцент кафедры «Математики» факультета математики-информатики Ферганского государственного университета Алиев Ибратжон Хатамович Студент 2 курса факультета математики-информатики Ферганского государственного университета

Ферганский государственный университет, Узбекистан

Аннотация. Дискретная математика всё больше получающая популярность также смогла найти и собственное применение благодаря введению новых информационных наук с использованием двоичной системы счисления, как в лице классической, так и квантовой информатики. В данной работе рассмотрен вопрос относительно нахождения не только известного ещё с 60-х годов XX века косвенного, но и непосредственного прямого применения операций импликации и эквиваленции, поиск коих продолжался до настоящего времени.

Ключевые слова: дискретная математика, импликация, эквиваленция, прямое применение, практическое применение, техническое осмысление, электрическая схема.

Annotation. Discrete mathematics, which is increasingly gaining popularity, has also been able to find its own application thanks to the introduction of new information sciences using the binary number system, both in the face of classical and quantum computer science. In this paper, the question of finding not only the indirect, but also the direct direct application of implication and equivalence operations known since the 60s of the XX century, the search for which has continued to the present time, is considered.

Keywords: discrete mathematics, implication, equivalence, direct application, practical application, technical understanding, electrical circuit.

На настоящий момент в дискретной математике и логике активно используются самые различные операций, позволяющие описывать проведение действий над суждениями. Так основными операциями являются конъюнкция, дизъюнкция и отрицание, так известные как логическое умножение, логическое сложение и логическое отрицание, соответственно. Они позволяли оперировать над различными суждениями, принимающими результат либо «истинно» – 1, либо «ложно» – 0.

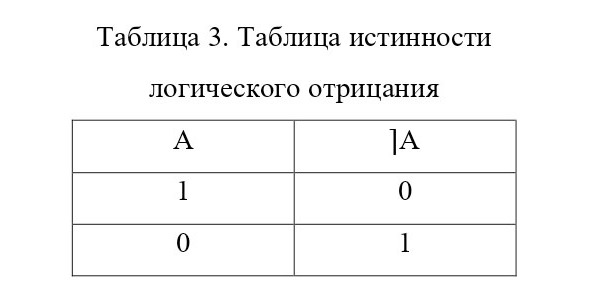
Каждый из операций при этом обладал своей таблицей истинности. Для конъюнкции это (Табл. 1), для дизъюнкции – (Табл. 2) и логического отрицания – (Табл. 3).

При этом для конъюнкции (логического «И») имеет место в практическом описании схема последовательного соединения (Рис. 1), описываемое в следующих случаях:

1. При отсутствии тока через «А» и через «В», в результате нет тока;

2. При наличии тока в «А», но в отсутствии через «В», в результате нет тока;

3. При отсутствии тока в «А», но в наличии в «В», в результате нет тока;

4. При наличии тока в «А» и в наличии в «В», в результате ток есть.

Рис. 1. Последовательное соединение

Для дизъюнкции (логического «ИЛИ») аналогичное представление можно увидеть в лице параллельного соединения (Рис. 2), описываемое уже в следующих случаях:

1. При отсутствии тока через «А» и через «В», в результате тока нет;

2. При наличии тока в «А», но в отсутствии через «В», в результате ток есть;

3. При отсутствии тока в «А», но в наличии в «В», в результате ток есть;

4. При наличии тока в «А» и в наличии в «В», в результате ток есть.

Рис. 2. Параллельное соединение

Для логического отрицания (логического «НЕ») же всё ещё более проще, ибо его можно представить как обычную обратную кнопку (Рис. 3), описывая действия следующим образом:

1. При наличии тока в «А», в результате тока нет;

2. При отсутствии тока в «А», в результате ток есть.

Рис. 3. «Кнопка» – логическое отрицание в цепи

Но вместе с этими операциями, присутствовали также операции импликации и эквиваленции, где импликация – логическое следствие или утверждение «Отсюда следует», а эквиваленция – логическая равносильность и или утверждение «Тогда и только тогда» обладало следующей таблицей истинности (Табл. 4), а эквиваленция – (Табл. 5).

При этом обе операции ещё не были применены на практике в прямом виде, так как это выглядело для конъюнкции и дизъюнкции. На сегодняшний день применяется преобразование для импликации (1) и для эквиваленции (2).

То есть импликацию можно представить как отрицание первого и дизъюнкцию со вторым утверждением, а эквиваленцию как конъюнкцию отрицаний обоих суждений на дизъюнкцию конъюнкции обоих суждений. Если же проверить на таблице истинности (1) и (2), то результат будет действительным (Табл. 6-7).

И представленные методы считались единственно возможными по сей день, пока наконец не был создан электрический элемент, своего рода соединение, при котором выполнялась бы в прямом случае импликация и эквиваленция.

Первое устройство – импликатор, состоит из вакуумной колбы 7 с катодом 3 и анодом 1, между коими помещена анодная сетка 2. Расстояние между катодом и анодом l выверено с той точностью, что оно меньше, либо равно свободному пробегу электронов, вылетевших из катода до анода. Также имеется изолированный электрод 6, подведённый с внешней стороны (за колбой) к штырю катода 3, но не соединённый с ним (Рис. 4).

Рис. 4. Схема импликатора

Таким образом, пусть анодная сетка 2 будет выступать в роли второго утверждения, катод 3 в роли первого, а анод 1 в роли результата. Вместе с этим вводится условие, что перед поступлением тока 4 к катоду 3 поставлен делитель 5, который реагирует на величину поступившего тока, если ток больше или равен определённого значения, принятого за истинность первого суждения, то оно подключается к катоду 3, в обратном случае к электроду 6 выходящий из анода. При этом исключением является случай, когда на анодной сетке 2 есть ток, при этом полагается, что на катод и к цепи катода ток не идёт вовсе.

Итак, в данной схеме можно рассмотреть четыре ситуации:

1. Если на катоде тока нет, и на анодной сетке тока нет, то ток течёт по электроду к аноду, в результате ток есть;

2. Если на катоде ток есть, но на анодной сетке тока нет, то электроны долетают до анода, в результате ток есть;

3. Если на катоде тока нет, но на анодной сетке тока нет, электронов в колбе также нет, из-за чего в результате тока нет;

4. Если на катоде ток есть и на анодной сетке ток есть, то электроны получают дополнительное ускорение, откуда выходит, что в результате ток также есть.

Данное устройство, как видно, хоть и с парой условностей, которых можно вполне заменить сводящими элементами, своего рода датчиками или переключателями, полностью выполняет функцию импликации. Но здесь интересно также упомянуть, что не использовалась ни конъюнкция, ни дизъюнкция, ни даже отрицание, если конечно не считать «переключатель» крайне отдалённым родственником отрицания, что было бы неуместно. Более того данная система выступает как единый элемент, полностью выполняющий поставленную задачу.

Говоря же о таком виде соединения, то его следует называть «близким смешанным» соединением, либо «Промихтовое» соединение, от латинского prore – «близко» и mixta – «смешанный», поскольку тут участвует одновременно и параллельное, и последовательное соединение, но уже более образно, из-за чего данное соединение выступает новым – третьим видом.

Ситуация же с эквиваленцией выступает аналогично, но отличие в том, что расстояние между катодом 3 и анодом 1 – L (для эквивалентора) должна быть строго больше длины пробега электронов, чтобы они не смогли долететь до него, без помощи анодной сетки, что, впрочем, и объясняет, почему импликатор соединённый «близко-смешанным» соединением. При применении же эквивалентора (Рис. 5) – устройства, выполняющий функцию эквиваленции, имеет место также 4 случая:

1. Если на катоде тока нет, и на анодной сетке тока нет, то ток течёт по электроду к аноду, в результате ток есть;

2. Если на катоде ток есть, но на анодной сетке тока нет, то электроны не долетают до анода, в результате тока нет;

3. Если на катоде тока нет, но на анодной сетке тока нет, электронов в колбе также нет, из-за чего в результате тока нет;

4. Если на катоде ток есть и на анодной сетке ток есть, то электроны получают дополнительное ускорение, откуда выходит, что в результате ток есть.

Рис. 5. Схема эквивалентора

Эквивалентор аналогично по типу соединения в таком случае соединён «дальне-смешанным» или «Лонмихтовым» соединением, от латинского longe – «далеко» и mixta – «смешанный».

Таким образом, можно продемонстрировать два элемента – импликатор и эквивалентор полностью выполняющие функции импликации и эквиваленции в современной электронике находя совершенное применение, позволяя в разы сокращать пространства, ибо данные схемы могут быть выполнены в сколь угодно малом размере, наряду с заменой «диодно-ламповой» части с наличием вакуума современными триодами с обычным дополнительным переключаемым соединением для импликатора и более модернизированные триодами с теми же переключателями и соединением для эквивалентора.

Представляя данную схему, можно надеяться, что оно принесёт свою пользу, внося свой вклад в развитие современной науки и техники, совершенствуя и привнося новое в науку, а также открывая перед всей человеческой цивилизацией новые ещё более грандиозные горизонты!

Использованная литература

1. Мендельсон Э. «Введение в математическую логику». – М. Наука, 1971.

2. Эдельман С. Л. Математическая логика. – М.: Высшая школа, 1975. – 176 с.

3. Игошин В. И. Задачник-практикум по математической логике. – М.: Просвещение, 1986. – 158 с.

4. Гиндикин С. Г. Алгебра логики в задачах. – М.: Наука, 1972. – 288 с.

5. Барабанов О. О. Импликация / Труды XI международных Колмогоровских чтений: сборник статей. – Ярославль: Изд-во ЯГПУ, 2013. С.49-53.