Все науки. №3, 2022. Международный научный журнал - читать онлайн

Каримов Боходир Хошимович

Кандидат физико-математических наук, доцент физико-технического факультета Ферганского Государственного Университета

Ферганский Государственный Университет, Узбекистан

Аннотация. В настоящей работе обнаружен и исследован фотовольтаический и фоторефрактивный эффект и определён единственное отличное от нуля фотовольтаический коэффициент k_ijk для кубическом кристалле ZnS. Этот коэффициент K₁₄ =2∙10^—9A∙см∙ (Вт) ^-1. Коэффициенты k_ijk более чем на порядок превышают соответствующие коэффициенты в LiNbO3:Fe. Использование в голографической записи фото-пьезоэлектриков дает преимущества. В этом случае запись осуществляется двумя когерентными лучами с поляризацией соответствующей фотовольтаическому току. При реконструирование записанной голограммы достигается путем освещения кристалла лучом когерентного света той же длины волны. Однако, поляризация этого луча выбирается таким образом, чтобы освещение не приводило к генерации фотовольтаического тока. Стирание записанной голограммы достигает путем равномерного освещение поверхности лучом света с предыдущей поляризации.

Ключевые слова: фотовольтаический эффект, кубический кристалл, фотовольтаические коэффициенты, голографический эффект, фото-пьезоэлектрик.

Annotation. In this paper, the photovoltaic and photorefractive effect is discovered and investigated, and the only non-zero photovoltaic coefficient kijk is determined for a cubic ZnS crystal. This coefficient K14 =2*10—9A*cm* (W) -1. The kijk coefficients are more than an order of magnitude higher than the corresponding coefficients in LiNbO3:Fe. The use of photo-piezoelectrics in holographic recording gives advantages. In this case, the recording is carried out by two coherent beams with polarization corresponding to the photovoltaic current. The reconstruction of the recorded hologram is achieved by illuminating the crystal with a beam of coherent light of the same wavelength. However, the polarization of this beam is chosen in such a way that the illumination does not lead to the generation of photovoltaic current. The erasure of the recorded hologram is achieved by evenly illuminating the surface with a beam of light from the previous polarization.

Keywords: photovoltaic effect, cubic crystal, photovoltaic coefficients, holographic effect, photo-piezoelectric.

ВВЕДЕНИЕ

Фото-ЭДС (или фотонапряжение) в полупроводниках независимо от ее природы не может превышать ширину запрещенной зоны, т.е. несколько Вольт. Например, в однородном полупроводнике Демберовское (диффузионное) фото напряжение для сколь угодно большой интенсивности возбуждающего света не превышает значения [1].

Где E_g – ширина запрещенной зоны полупроводника, n₁ и n₀ – соответственно неравновесная и равновесная концентрации носителей, N_c – плотность состояний.

Другим примером может служить возникающие фотонапряжение при освещении p-n —перехода [2].

которое также не превышает E_g. Здесь и – соответственно концентрации электронов в n – области и дырки в р – области. и – энергии уровня Ферми в n – и р – областях.

Исключение из этого правила составляли лишь полупроводниковые текстуры в которых наблюдается эффект аномально больших фото напряжений (АФН эффект), обусловленный сложением элементарных фото-ЭДС Дембера (1) или элементарных фото-ЭДС (2), развивающихся на отдельных р-n —переходах текстуры [3].

В таких текстурах из напиленных слоев CdTe, Ge, Si, GaAs, PbS, CdSe и т. д. фото напряжения могут достигать значений порядка нескольких сотен Вольт на сантиметр длины в направлении сложения элементарных фото-ЭДС (1) или (2).

В последние годы стало ясно, что в термодинамических неравновесных условиях возможны токи иной природы, обусловленные отсутствием среды центра симметрии. Важнейшим этого класса эффекта является аномальный фотовольтаический эффект (АФ эффект).

АФ эффект заключается в том, что при равномерном освещении короткозамкнутого сегнетоэлектрика через него протекает стационарный ток, который в [4,5] был назван фотовольтаическим. Было показано, что именно фотовольтаический ток приводит к аномальному фотовольтаическому эффекту (АФ эффект) в сегнетоэлектрике.

Аномальный фотовольтаический эффект, обнаруженный для сегнетоэлектриков впервые в [4,5] является частным случаем АФ эффекта, описываемого для кристаллов без центра симметрии тензором третьего ранга [5,6]:

Согласно (3), при равномерном освещении линейно поляризованным светом однородного кристаллов без центра симметрии (сегнето, пиро или пъезоэлектрического кристалла) в нем возникает фотовольтаический ток J_i, знак и величина которого зависят от ориентации вектора поляризации света с проекциями.

Компоненты тензора a_ijk отличны от нуля для 20 ацентричных групп симметрии. Если электроды кристалла разомкнуть, то фотовольтаический ток генерирует фотонапряжения

где

и соответственно

темновая и фотопроводимость, расстояние между электродами. Генерируемое фотонапряжения порядка 10³—10⁵В, превышающее величину ширины запрещенной зони E_g на два – четыре порядка.

В соответствии с (3) и симметрией точечной группы кристалла можно написать выражения для фотовольтаического тока. Сравнение экспериментальной угловой зависимости (b) с (3) позволяет определить фотовольтаический тензор a_ijk или фотовольтаический коэффициент

(a* – коэффициент поглошения света).

1. ФОТОВОЛЬТАИЧЕСКИЙ ЭФФЕКТ В ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛАХ ZnS

В работе изложен результаты исследования объемного фотовольтаического эффекта в пьезоэлектрических кристаллах ZnS, принадлежащих к кубической точечной группе m.

Исследовались кубические кристаллы ZnS, вырашенные гидротермальным методом в растворах H₃PO₄ и KOH в лаборатории гидротермального синтеза института кристаллографии Российской АН.

В отличие от сегнетоэлектриков [4, 5] фотовольтаический эффект в ZnS можно наблюдать только в поляризованном свете [8,9]. В соответствии (3) и симметрией точечной группы при освешении кристалла в z направлении оси 4 порядка (оси z) выражение фотовольтаического тока в z направлении имеет вид:

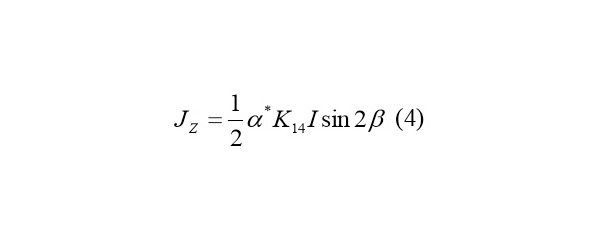
где – угол между плоскостью поляризации света и осью х.

Измерение фотовольтаического тока J_z и генерируемого им поля

(s_ф– фотопроводимость) производилось путем снятая стационарных вольт-амперных характеристик [5].

На рис.1 представлена ориентационная зависимость в направлении [001], снятая при Т = 143К при освещении светом с длинной волны l=500 нм (a*=5 см^-1) и интенсивностью I=2.3∙10^—3 Вт∙см^-2. Кристалл освещается плоско поляризованным светом в направлении [001].Сравнение этой угловой зависимости с (4) даёт

K₁₄ =2∙10^—9A∙см∙ (Вт) ^-1.

Таким образом, значение модуля К₁₄ в исследованных кристаллах ZnS существенно выше, чем у известных сегнето- и пьезоэлектриков [4, 5,6].

В интервале Т=140—300⁰К модуль К₁₄ обнаруживает слабую температурную зависимость. Благодаря этому, а также из-за сильной температурной зависимости фотопроводимости s_ф, генерируемое в направление оси z поле

изменялось в пределах от 1В·см^-1 (Т=300⁰ К) до 40В·см^-1 (Т=143⁰К) и не зависело от интенсивности света I.

Рис.1 Ориентационная зависимость плотности фотовольтаического тока J_z в направлении [001]. (T=143K, I=2.3∙10^—3 Вт∙см^-2, =500 нм)

В кристаллах ZnS, выращенных гидротермальным методом фотовольтаический эффект имеет в основном примесный характер. Это видно из рис.2 где представлены спектральные распределения фотопроводимости s_ф (1) фотовольтаического тока (2), отнесенные к единицы падающей энергии и края оптического поглощения (3).

Примесная полоса в спектральном распределении имеет место вблизи l=500 нм. Там же расположен примесный максимум фотопроводимости. Для кристаллов, выращенных в кислотной или щелочной среде примесный максимум, имеет разное положение и сдвигается в пределах 450—500 нм.

Рис.2. Спектральное распределение фотовольтаического тока J_z (2), фотопроводимости s_ф (1) и оптического поглощения * (3) приТ=143К. =45⁰

2. ФОТОРЕФРАКТИВНЫЙ ЭФФЕКТ В КУБИЧЕСКИХ КРИСТАЛЛАХ ZnS

Влияние неравновесных носителей на двулучепреломленние сегнето и пьезоэлектрических кристаллах получило в литературе название фоторефрактивного эффекта (ФР эффект) и нашёл широкое использование для регистрации объемных голограмм. ФР эффект заключается в следующем. В результате локального освещения или пьезоэлектрического кристалла интенсивным проходящим светом (сфокусированным лучом лазера) в объеме кристалла внутри светового пучка имеет место обратимое изменение двулучепреломления, главным образом за счёт изменения показателя преломления необыкновенного луча n_e. Величина этого изменение достигает 10^—4 -10^-3 для некоторых пироэлектриков (LiNbo₃ LiTa0₃), а время его существования может изменяться в широких пределах, от миллисекунд в BaTiO₃ до месяцев в LiNbO₃. Запись голограммы осуществляется благодаря объемной модуляции значения Dn, соответствующей модуляции записывающего луча. Разрешающая способность записи исключительно высокие, 10²—10⁴ лин/мм. [7,9].

Главное преимущество этого метода оптической памяти по сравнению с фотографическими слоями заключается в возможности параллельной записи, считывания и стирания.

Как показано знак и величина фотовольтаического тока зависит от симметрии кристалла и поляризации света. Фотовольтаический ток приводит к генерации в том же направлении аномально больших фотонапряжений. Таким образом, за время экспозиции t в кристалле возникает макроскопическое поле.

Благодаря линейному электрическому эффекту поле приводит к ФР эффекту:

где r_ij– электрооптические коэффициенты. Уравнение (6) записано в главой системе координат. После освещение поле сохраняется в кристалле длительное время благодаря захвату неравновесных электронов и дырок. Этот механизм захвата ответствен за оптическую память. Стирание может осуществляться путем отжига кристалла при 170С. Имеются и другие метода стирания.

В высокоомных кристаллах ZnS, можно наблюдать ФР эффект, знак и амплитуда которого зависит от ориентации плоскости поляризации света (4) рис.1. Использование в голографической записи фотопьезоэлектриков дает преимущества. В этом случае запись осуществляется двумя когерентными лучами с поляризацией соответствующей фотовольтаическому току Ј_z и полю Е_z в z-направлении (). Реконстуирование записанной голограммы достигается путем освещения кристалла лучом когерентного света той же длины волны. Однако, поляризация этого луча выбирается таким образом, чтобы освещение не приводило к генерации фотовольтаического тока в z – направлении (). Стирание записанной голограммы достигает путем равномерного освещение поверхности лучом света с предыдущей поляризации (). Таким образом, использование света с разным направлением плоскости поляризации позволяет реконструировать голограмму, записанную в фотопьезоэлектрике без заметного повреждения. Рис.3 показывает голографический запись, восстановление, и стирание записи в фотопьезоэлектрике.

Также АФ эффект в кристллах без центра симметрии может быть применён как новый тип элементов-фотовольтаических преобразователей энергии. КПД преобразователей световой энергии в электрическую энергию на основе фотовольтаического эффекта пака низок.

Однако, сегнето, ипеъзоэлектрики могут использоваться для генерации опорных напряжений низкой мощности. При этом спектральный чувствительность этих элементов варьируется широкой области: от вакуумной ультрафиолетовой до красной видимой области.

Имеется возможности применения этих процессов в бесеребрянной фотографии и видиконов, а также в нанотехнологии.

ЗАКЛЮЧЕНИЕ

Обнаружен и исследован фотовольтаический и фоторефрактивный эффект и определён единственное отличное от нуля фотовольтаический коэффициент

K₁₄ =2∙10^—9A∙см∙ (Вт) ^-1 для кубическом кристалле ZnS. Коэффициенты K₁₄ более чем на порядок превышают соответствующие коэффициенты в LiNbO3:Fe.

Показана возможность использование фотопьезоэлектриков в голографической записи. В этом случае запись осуществляется двумя когерентными лучами с поляризацией соответствующей фотовольтаическому току. Реконстуирование записанной голограммы достигается путем освещения кристалла лучом когерентного света той же длины волны. Однако, поляризация этого луча выбирается таким образом, чтобы освещение не приводило к генерации фотовольтаического тока. Стирание записанной голограммы достигает путем равномерного освещение поверхности лучом света с предыдущей поляризации. Также стирание может осуществляться путем отжига кристалла при 170С.

Автор благодарит С. Шамирзаеву за обсуждение.

Использованная литература

1. Рывкин. С. М. Фотоэлектрические явления в полупроводниках. М.: Физматгиз. 1963. 494С.

2. Бьюб Р. Фотопроводимость твердых тел. М.: ИЛ. 1962. 558С.

3. Э.И.Адирович. Фотоэлектрические явления в полупроводниках и оптоэлектроника. Ташкент: Фан. 1972. 343 С.

4. Glass A.M., Voh der Linbe D., Nerren T.J.//High- voltage Bulk Photovoltaic effect and the Photorefractive process in LiNbO₃. J. Appl. Phys. Let, 1974. N4. v.25. p.233—236.

5. Фридкин В. М. Фотосегнетоэлектрики. М.: Наука. 1979. С.186—216.

6. В.И.Белиничер. Исследования фотогальванических эффектов в кристаллах. Дисс. на соискание. докт. физ-мат. наук. Новосибирск. 1982. 350 С.

7. Леванок А. П., Осипов В. В. Механизмы фоторефрактивного эффекта.// Изв. Ан. Россия, 1977. Т.41. №4. C.752—769.

8. Стурман Б. И., Фридкин В. М. Фотогальванические эффекты в средах без центра инверсии. М.: Наука. 1992. 208 С.

9. Фридкин В. М. //Объемный фотовольтаический эффект в кристаллах без центра симметрии. Кристаллография. 2001. Т.46 №4. С.722—726.

Алиев Ибратжон Хатамович

Студент 2 курса факультета математики-информатики Ферганского Госудрственного Университета

Ферганский Государственный Университет, Узбекистан

Аннотация. Развитие физики резонансных ядерных реакций, о которой неоднократно говорилось в целом ряде самых различных публикаций, становиться причиной для дальнейшего исследования применения данного метода относительно различных ядер и проведения подробных расчётов.

Ключевые слова: ядерная реакция, протон, изотоп магния, кулоновский барьер, длина волны, частицы, истинное сечение.

Annotation. The development of the physics of resonant nuclear reactions, which has been repeatedly discussed in a number of very different publications, becomes a reason for further investigation of the application of this method with respect to various nuclei and for conducting detailed calculations.

Keywords: nuclear reaction, proton, magnesium isotope, Coulomb barrier, wavelength, particles, true cross section.

Пятая ядерная реакция, исследуемая на сегодняшний день, что и придаёт ей данный коэффициент, представляется следующим образом (1).

Протон с энергией в 4,457595117 МэВ и массой в 1,00728 а. е. м., налетает на алюминий-27 с атомной массой в 26,98153863 а. е. м., с выделением изотопа магния-24 с массой 23,9850417 а. е. м., а также альфа-частицы с массой 4,001506179 а. е. м.

Изначально, необходимо определить, какое количество энергии затратит протон, приближаясь к ядру алюминия, а именно высоту кулоновского барьера (3), определив радиус ядра алюминия-27 в (2).

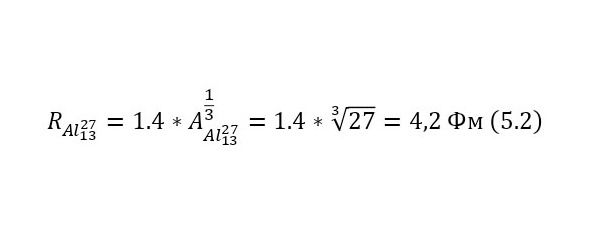
Следовательно, нынешняя энергия протона, после затраты на кулоновский барьер, составляет 0,4 эВ. Теперь, необходимо вычислить энергетический выход данной ядерной реакции, с указанными массами в (4).

Поскольку эта реакция экзо-энергетическая, то нет смысла вычислять для неё порог реакции, остаётся лишь записать пару энергетических уравнений (5—6) и затем вычислить энергии, приобретаемые магнием-24 и альфа-частицей.

Из этих энергетических уравнений стало ясно, что кроме выхода реакции, добавляется и оставшаяся кинетическая энергия, благодаря чему общая энергия, распределяемая между частицами, составляет 2,115204957 МэВ из равенства (7). Теперь, для распределения этих энергий достаточно воспользоваться (8) и (9).

И наконец, остаётся определить сечение ядерной реакции и число взаимодействий. Изначально, необходимо вычислить длину волны налетающих протонов, для этого достаточно определить их импульс через (11), перед этим вычислив скорость в (10), а затем уже длину волны в (12).

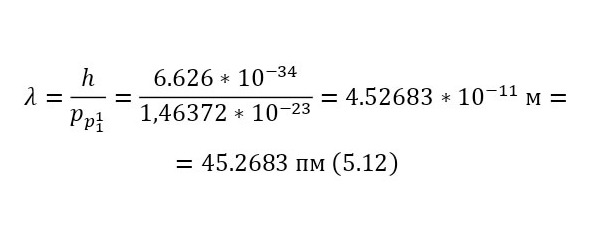
Переходя уже к исчислению сечений, достаточно воспользоваться (13), но также необходимо использование коэффициента, о котором говорилось ранее, по этой причине применяется и (14), и только после вычисляется истинное сечение (15), для некоторых подсчётов, этот коэффициент становится равным единице, поэтому просто не указывается, но в данном случае, если подсчитать таким же образом.

Теперь, когда сечение известно, для этой реакции, остаётся ввести число взаимодействий (19), перед этим вычислим число атомов на кубометр (16) и указав толщину пластины в 78 мкм, поскольку пробег протона (максимальное расстояние на котором может пройти при определённой энергии) с энергией 3 МэВ составляет это значение.

А также необходимо определить в (18) начальное число бомбардирующих протонов, указав, что их общая сила тока 25 А, а время одного акта, который вытекает уже из параметров циклотрона, описываемый в предыдущих главах составляет 328,13 нс, что гораздо больше времени даже самой долгой реакции, откуда можно вычислить заряд (17), а из него уже и число протонов (18).

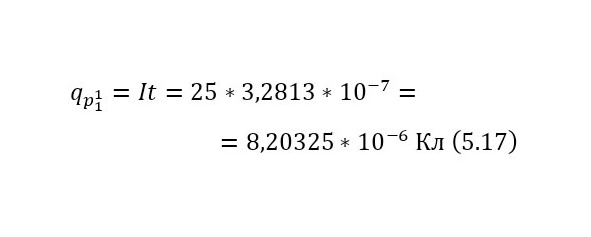
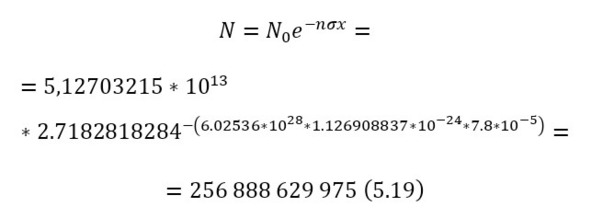
Это число всех частиц, прошедших сквозь пластину и не вошедших в реакцию, а для того, чтобы вычислить те, которые вошли в реакцию, достаточно определить разность в (20), а затем уже вычислить из них заряд, учитывая, что альфа-частица несёт 2 элементарных заряда (21) и силу тока (22).