Глава 1 Внутри пространственно-временного континуума
Тайны времени. Прошлое, настоящее и будущее одинаково реальны
В одну реку можно войти дважды, если это река времени. И не только войти, но и изменить ход событий. Однако потом это будет уже другая река. Небольшая часть человечества издревле догадывалась об этом, но лишь сегодня наука вплотную подошла к разгадке тайны.
Впервые физическое определение времени дано в «Началах» Исаака Ньютона: «Абсолютное, истинное, математическое время само по себе и по своей сущности без всякого отношения к чему-либо внешнему протекает равномерно и иначе называется длительностью». Подобное понимание времени достаточно долго доминировало в физике, вплоть до начала XX века.
Альберт Эйнштейн в специальной теории относительности показал, что абсолютного времени не существует. Его течение зависит от инерциальной системы отсчёта, в которой происходят измерения. В движущихся с большой скоростью системах время течёт медленнее. Чем ближе приближается наблюдатель к скорости света, тем больше эффект замедления времени. Причём этот эффект ещё более возрастает, если двигаться с ускорением. Так, путешествие до галактики М31 (Туманность Андромеды), расстояние до которой около 2,52 млн световых лет, космонавт, летящий в корабле с ускорением в 1g (что соответствует земной гравитации), по своим часам преодолеет за 53 года. На Земле же пройдёт 3 млн лет. Польский математик Герман Минковский дал топологическую интерпретацию эффекта замедления времени в движущейся системе отсчета. Он объяснил замедление времени при приближении к скорости света увеличением проекции временного интервала четырёхмерного многообразия континуума, где время выступает как четвёртое измерение к трём измерениям пространства. Таким образом, специальная теория относительности открывает механизм путешествия в будущее.
Общая теория относительности демонстрирует другой механизм перемещения во времени. Для попадания в будущее необходимо искривить пространство вокруг наблюдателя. Чем более искривлено пространство, тем медленнее течёт для него время, поскольку проекция временного интервала четырёхмерного континуума резко увеличивается. В случае замыкания пространства (примером служат чёрные дыры) время практически останавливается, поскольку длина проекции временного интервала стремится к бесконечности. По мнению Н.С. Кардашёва, огромные чёрные дыры, которые находятся в центрах большинства галактик, можно использовать как машины времени для попадания в будущее на сколь угодно далеко. Если пройти через них по расчётной траектории, тогда градиент кривизны будет незначителен и не окажет существенного влияния на движущегося наблюдателя.
Теория относительности не запрещает путешествие в прошлое. Для этого достаточно вызвать «скрутку» пространства, которая бы пересекла мировые линии прошлого, ибо время как четвёртое измерение приравнено к пространству. Но здесь нас ждёт «парадокс дедушки». Предположим мы вернулись в прошлое и встретили там своего деда, взяли да и убили его. Тогда возникает вопрос, а как мы тут сами оказались? Этот парадокс был решён физиком Хью Эвереттом. Согласно его точки зрения, такие действия могут привести к отщеплению линии развития Вселенной, и это будет уже другой параллельный мир, из которого мы переместились в прошлое. Между тем последние физические исследования в квантовой сфере показали, что эффекта бабочки не существует (его проявления крайне незначительны) и изменения в прошлом не могут вызвать кардинальных изменений в будущем. Б. Ян и А.Н. Синицын из Лос-Аламосской Национальной лаборатории в эксперименте на квантовом компьютере наблюдали, как временная шкала исправляла сама себя, и чем в более удалённом прошлом происходят изменения, тем меньше они будут заметны в настоящем. Однако проблема всё же остаётся и требует дальнейших теоретических исследований, потому что процесс перехода этого эффекта в макромир ещё не изучен.
И именно квантовая механика открывает другие пути для путешествия во времени. Соотношение неопределённости Гейзенберга, касающееся вероятностного положения микрообъекта и его импульса, приводит к пространственному туннельному эффекту. Поскольку положение микрообъекта не определено, он может обнаруживаться в разных областях пространства. В результате ток проходит через изолятор (эффект Джефферсона), а луч лазера через зеркало, что, казалось бы, невозможно с точки зрения классической физики и здравого смысла.
Вместе с тем такая же неопределённость существует между энергией и временем. Поэтому возможен туннельный эффект и во времени: если его усилить и задать направление, то можно путешествовать как в прошлое, так и в будущее, сформировав своего рода временную кротовую нору. В современной физике существуют две концепции времени: динамическая и статическая. Согласно динамической концепции, прошлого уже нет, будущего ещё нет, а реально только настоящее. Она согласуется со здравым смыслом, но имеет один существенный недостаток – отсутствие критерия настоящего. Статическая концепция времени исходит из того, что прошлое, будущее и настоящее обладают одинаковым статусом реальности, т. е. они реально существуют [1]. Согласно статической теории, различия между прошлым, настоящем и будущем того же рода, что и различия между точками пространства. Тогда становится более понятным возможность путешествия во времени, поскольку это просто переход на другой фрагмент реальности.
Особого внимания заслуживает субъективное восприятие времени. По современным данным его течение зависит от скорости обработки мозгом информации. Чем быстрее происходит обработка информации субъектом, тем более замедленным вокруг него выглядит реальность. В мозге была обнаружена структура – супрахиазматическое ядро, объёмом 1 мм3, состоящая из 100 тыс. клеток, которая и задаёт темп времени для всего организма [2].
В 2007 году Дэвидом Иглманом и его коллегами из Университета штата Техас был проведён интересный эксперимент. Испытуемых вводили в состояние стресса, сбрасывая с 30-метровой высоты на защитную сетку. На руке у каждого был экран, мерцание которого не позволяло видеть изображение, находящееся на нём, поскольку его частота была столь высока, что мозг не мог распознать информацию. Во время падения темп обработки информации увеличивался, что соответствовало замедлению информационных потоков, поступающих в мозг. Участники субъективно оценивали длительность своего падения на 36 % дольше, чем это было на самом деле. Тем не менее они не смогли идентифицировать ускоренно демонстрирующееся изображение на наручном экране. Результаты эксперимента указывают на то, что субъективное время не является единым целым, которое ускоряется или замедляется, а состоит из отдельных компонентов. Авторы исследования предполагают, что феномен замедления восприятия времени в стрессовых ситуациях происходит при вовлечении в эмоциональную память миндалевидного тела головного мозга [3].
Сегодняшняя реальность такова, что развитие цивилизации позволило создать технику и технологии по преодолению пространства, но до сих пор не созданы хронотехнологии, обеспечивающие путешествие во времени. Остаётся надеяться, что в недалёком будущем появятся технологические решения и этой проблемы.
Топологическое многообразие микро-, макро- и мегамира
Топология, по сути, является наукой о пространстве. Её возникновению предшествовал длительный период развития математической мысли. Геометрия Евклида в течение двух тысячелетий рассматривалась в качестве единственной геометрии нашего мира. Однако работы Лобачевского и Гаусса показали, что она является лишь одним из типов геометрий, которые могут быть реализованы не только как объекты математического мышления. Великое достижение математической мысли конца XIX и начала XX века, как отмечал немецкий математик Гильберт, заключалось в том, что удалось изгнать чертежи из математики и свести геометрию к алгебре. Возникновение алгебраической геометрии явилось предтечей топологии, которая пошла ещё дальше в своём развитии. В отличие от алгебраической геометрии, изучающей метрические свойства пространства, топология сконцентрировала своё внимание на его качественных свойствах.
С точки зрения топологии, выделяются количественные и качественные (собственно топологические) свойства пространства [4]. К количественным свойствам относятся кривизна, измерение углов, измерение площадей. Качественные свойства пространства представлены размерностью, ориентированностью, связанностью.
Немецкий математик Гаусс ввёл понятие кривизны или деформации пространства, а также разработал метод, позволяющий исследовать искривление той или иной поверхности. Он создал обобщающую систему координат, где угол между осями может быть криволинейным. Кратчайшее расстояние между двумя точками в обобщённой системе координат получило название геодезической линии. Изменился постулат о параллельных прямых в евклидовой геометрии, согласно которому через точку, лежащую вне данной прямой, можно провести только одну прямую параллельную данной. Теперь между точкой, лежащей вне геодезической линии, можно было в зависимости от кривизны не провести ни одной геодезической линии параллельной данной или провести их бесконечное количество. В первом случае кривизна положительна, и пространство замкнуто. Образом такого пространства является шар, на котором все геодезические линии, как дуги больших радиусов, пересекаются, а сумма углов треугольника больше 180 градусов. Во втором случае геодезические линии имеют бесконечную длину, пространство разомкнуто, оно имеет отрицательную кривизну. На поверхности с отрицательной кривизной траектории разбегаются и нигде не пересекаются. Сумма углов на подобной поверхности будет меньше 180 градусов. Моделью такой поверхности является седло, а также обратная сторона тора или бублика. Геометрия Евклида оказалась геометрией плоского пространства с кривизной равной нулю. Кривизна во взаимодействии с качественными свойствами порождает огромное топологическое разнообразие пространства.
Рассмотрим такое топологическое свойство, как размерность. Точка как математический объект не имеет измерения. Движение точки порождает линию. Она имеет одно измерение – длину и представляет пример одномерного пространства. Перпендикулярное движение точки относительно линии порождает двухмерное пространство или плоскость. Продолжим алгоритм и получим трёхмерное, а затем четырёхмерное и N-мерные пространства. Представить себе многомерную метрику нельзя, возможности нашего мозга ограничены, но вычислить её можно, используя для этого многоиндексные массивы или матрицы, где количество столбцов и будет определять мерность пространства. Необходимо использовать компьютеры и выполнить проекции, перебрав многомерное многообразие в двухмерных или трёхмерных проекциях. В настоящее время аппарат многомерной метрики широко используется в различных областях науки.
Важной характеристикой размерности пространства является чётность или нечётность. Например, в четырёхмерном пространстве любые две точки будут разделены чем-либо трёхмерным, в двухмерном – одномерном. В подобном пространстве возможно существование таких пар точек, для которых сфера или плоскость, заключающая одну из них, не сможет отделить эти объекты друг от друга. Препятствие в этом случае всегда можно обойти и достичь одной и другой точки, не проникая в сферу. Жук сможет выползти из закрытого ящика стола, желток можно отделить от белка, не разбивая яйцо. Тюрьма в таком пространстве невозможна. Заключённые всё равно убегут, так как препятствия всегда можно обойти.
Ориентированность – ещё одно важное качественное свойство пространства. Под ориентированностью понимается сохранение при движении в таком пространстве положений верх-низ и право-лево. Действительно, двигаясь в этом пространстве, и даже совершая кругосветное путешествие, придя в отправную точку или место нашего движения, мы не заметим никаких изменений – положения лево-право и верх-низ не изменились. Такое пространство называется ориентированным. Неориентированное пространство – это такое пространство, при движении в котором, возможно изменение состояний, приводящих к ситуации, когда левое станет правым, а пол поменяется местами с потолком. Как это возможно? Немецкий математик Мёбиус продемонстрировал топологический конструкт, получивший название в его честь, реализующий пример неориентированного пространства. Если взять вытянутую в прямоугольник бумажную ленту, перекрутить её на пол-оборота и склеить противоположные края, то мы получим так называемый лист Мёбиуса. С одной стороны, его геометрия в небольших масштабах не отличается от евклидовой, но с другой – если жук проползёт из исходной точки этого конструкта и вернётся назад, то он окажется на противоположной стороне листа, и низ станет верхом, а левое будет правым. Не пересекая края листа, можно кисточкой покрасить одной краской обе его поверхности. Это пример так называемой односторонней поверхности и неориентированного пространства.
Может ли такое произойти с нашим трёхмерным пространством? В принципе, это возможно. Если на больших расстояниях, следуя указанному алгоритму, деформировать пространство, то космонавт, вернувшись после путешествия, обнаружит, что левое стало правым, а низ превратился в верх.
Топология особым способом описывает свойства геометрических фигур. С точки зрения этой науки, пирамида, куб, шар являются проявлениями одного и того же топологического образца, поэтому эти фигуры одинаковые, несмотря на их различную геометрию. Она изучает свойства геометрических фигур, которые сохраняются при деформациях, лишь бы это не сопровождалось разрывами и склеиваниями. Деформируя пирамиду, можно перевести её в шар, но ни при каких усилиях шар не превратить в тор.
Важнейшей топологической характеристикой является связанность. Если взять на круге какую-нибудь кривую, то деформациями мы можем стянуть её в точку. Такое пространство называется односвязанным. Между тем, если эта кривая будет находиться на кольце, то сжать её в точку не удастся. Только сделав разрез, она превратится в односвязанную поверхность. Связанность измеряется количеством разрезов области пространства N, которые переводят его в односвязанное, увеличенное на единицу. Связанность характеризуется прерывностью пространства, наличием в нём разрывов. Какое это имеет отношение к физическому пространству нашей Вселенной? Выясняется, что самое непосредственное. С точки зрения теории суперструн, пространство имеет, по крайней мере, девять измерений, три из которых расширились в момент рождения Вселенной, а остальные шесть остались на микроуровне, искривлены и компактифицированы. Более того, в пространстве имеются прерывности. При взаимодействии с таким сложным топологическим конструктом суперструны реализуют физические процессы, происходящие в микромире, благодаря чему теория суперструн единообразно описывает основные виды физических взаимодействий.
Топология разводит такие понятия, как бесконечность и безграничность, которые раньше отождествлялись [5]. Безграничность – это топологическое свойство пространства, указывающее, что у него нет границ ни в каком направлении. Бесконечность – метрическое свойство, согласно которому можно продвигаться как угодно далеко. Примером безграничного, но не бесконечного пространства является шар. Перемещаясь по шару, мы не встретим никаких границ при своём движении, но это пространство метрически конечно, так как имеет вполне определённую площадь. Напротив, плоскость – это пример бесконечного и безграничного пространства. В целом для топологических характеристик пространства необходимо применять понятия, характеризующие их свойства, как замкнутое (метрический признак «конечное») или открытое (метрический признак «бесконечное»), ориентированное или неориентированное, а также показатель связанности.
В настоящее время топология является ключом к пониманию многих процессов, происходящих как в макро-, так и в микромире. Какой в наших представлениях окажется Вселенная на разных уровнях масштаба, во многом будет зависеть как от развития самого топологического знания, так и от его применения в различных научных сферах.
Апория Зенона «Дихотомия». Предельный квант пространства
Апории Зенона были придуманы для того, чтобы обосновать идею своего учителя Парменида, который в противовес Гераклиту, утверждавшему положение о текучести бытия, рассматривал бытие как целостное и неподвижное. А движение с его точки зрения проявлялось как человеческая иллюзия.
Апория в переводе с греческого означает безысходность или безвыходное положение, являющееся хотя и вымышленным, но логически верным. Апория представляет собой правильное логическое утверждение или вывод, не соответствующий эмпирической реальности.
Апории Зенона долгое время не давали покоя философам, а потом и учёным, и только современная физика смогла разрешить эти головоломки. Рассмотрим самую простую апорию – «Дихотомия». Предположим, говорит Зенон, что путник идёт из пункта А в пункт Б. Прежде чем он пройдёт весь путь, он должен преодолеть половину этого расстояния, но до того, как он пересечёт половину, он должен пройти половину половины и так далее. Процесс деления пространства уходит в бесконечность, и движение становится невозможным [6]. Здесь не спасёт и понятие предела. Сумма бесконечно малых величин станет бесконечно большой, и чтобы преодолеть бесконечность, потребуется вечность. Действительно, если процесс деления пространства не остановится (с точки зрения математики, даже одномерный и ограниченный объект – линия, состоит из бесконечного количества точек, так как точка не имеет размера), тогда логика Зенона справедлива.
Современная физика пришла к пониманию, что существует предельный квант пространства, и он равен 10-33 см. Данный размер кванта возникает из соотношения калибровочных коэффициентов трёх миров: микро-, макро- и мегамира, являющихся физическими константами, которые представлены постоянной Планка, гравитационной постоянной и скоростью света. Это значит, что до данного уровня сохраняются все известные свойства пространства, в том числе и его делимость. Поэтому процесс, постулированный Зеноном, прекратится, как только будет достигнут уровень квантового размера, поскольку только до квантового уровня пространство обладает известными науке свойствами.
Аналогичный пример можно привести из химии. «Минимальными носителями» химических свойств являются атомы. Элементарные частицы, из которых они состоят: электроны, протоны, нейтроны и другие частицы химическими свойствами уже не обладают. Поэтому химия – это наука об атомно-молекулярных взаимодействиях. За границами атома его компоненты изучает физика элементарных частиц, и свойства этих частиц качественно иные.
Конечно, можно возразить, что же нам мешает взять ещё меньшую величину? Ответ на это возражение заключается в следующем – за границами кванта свойства пространства становятся качественно иными, и процесс деления там уже невозможен. К сожалению, наука ещё не скоро выйдет на уровень кванта пространства, это, вероятно, станет реальным только в отдалённом будущем. Тем не менее существует подход, разрабатываемый лауреатом Нобелевской премии Герардом Хоофтом. Его идея базируется на существовании параллельной Вселенной, имеющей голографическую природу, которая транслируется в наш мир. Согласно расчётам голландского физика, пространство нашей Вселенной имеет пиксельную природу по аналогии с экраном жидкокристаллического телевизора или компьютера. При этом размер пиксела, т. е. кванта пространства составляет 10-16 метра, а это уже, в принципе, доступно для современной техники.
Апория «Стрела» в свете современных физических теорий
Вопросы, поставленные древнегреческими мыслителями, остаются актуальными и в настоящее время. Логика Зенона вскрыла парадоксальную природу пространственно-временной реальности. Его апория «Стрела» обнаруживает иллюзорность обыденных представлений о свойствах пространства и времени. Зенон показывает, что рассуждения о движении постулируют вывод прямо противоположный нашему чувственному опыту. В этой апории утверждается, что летящая стрела покоится, и её движение является заблуждением, порождаемым нашими органами чувств. Его доказательство выглядит довольно необычным. Пусть стрела летит из точки А в точку С, и на своём пути она проходит точку B. Возникает вопрос, когда стрела проходит точку B, она находится в точке В? Казалось бы, ответ является очевидным: а где же ей ещё находиться… Между тем Зенон делает ошеломляющий вывод о том, что если стрела находится в точке В, значит она покоится. Тогда всё пространство на интервале АС можно представить как совокупность точек состояний покоящейся стрелы. Движение стрелы отсутствует.
Для опровержения этой логики необходимо допустить, что в какой-то момент времени стрела вообще не находится в пространстве, и что само пространство нельзя рассматривать как совокупность точек, не имеющих измерения. Самое главное, что пространство не является чем-то фундаментальным, каким оно воспринимается нашими чувствами и описывается такими теориями, как квантовая механика и теория относительности.
Каким же образом можно представить состояние стрелы, которая в определённый момент времени не должна находиться в пространстве? Ответ можно найти в квантовой механике, описывающей физику микромира. Природа микрофизической реальности носит вероятностное соотношения импульса объекта и его положения в пространстве. Поскольку положение не определено, то объект может обнаруживать себя, исчезая в одной точке пространства и возникая в любой другой, определяемой вероятностью его появления. Это так называемый туннельный эффект, являющийся следствием необычности квантового мира. За его экспериментальное подтверждение Джефферсон получил Нобелевскую премию. Он взял проводник электрического тока, разрезал его и поместил между двумя концами тончайший слой изолятора. Как известно, изолятор не проводит электрический ток, и в макромире так бы и случилось. Тем не менее ток через изолятор прошёл, электроны туннелировались через препятствие. Ещё более наглядную демонстрацию туннельного эффекта провели отечественные физики. Они поместили внутри световода тончайшее зеркало. Как известно, зеркало отражает свет, и он не может пройти через него. Однако лазерный луч миновал зеркало, сохранив закодированную в нём информацию, поскольку фотоны осуществили эффект туннелирования. Поэтому туннельный эффект частично разрешает парадокс Зенона, так как объект исчезает в одной точке пространства и появляется в другой, за счёт чего и происходит движение.
В современных физических теориях, описывающих микромир, пространство не может рассматриваться как бесконечная совокупность точек. В них постулируется существование кванта пространства и времени. Для пространства он составляет 10-35 метра, а для времени 10-44 секунды. Следовательно, пространство и время квантованы и только до этих масштабов сохраняют известные нам свойства. Более того, и само пространство состоит как бы из пикселов по аналогии с дисплеем компьютера. Исходя из голографической и информационной теорий, немецкий физик Хоофт пришёл к выводу, что кванты пространства нашей Вселенной имеют больший размер и составляют 10-16 метра. За счёт вероятностной природы возникает неопределённость на микроуровне самого пространства, что порождает «шум», который мешал регистрации гравитационных волн. Если само пространство имеет неопределённость, то и положение объекта не определено. В теории суперструн возможны нарушения непрерывности пространства, возникновения разрывов и «дырок», поскольку пространство представляет собой жёсткую и упругую среду. Попадая в такие разрывы, микрообъект может исчезать в них. Постулирование многомерности, гравитационных аномалий, возникновение червоточин также может приводить к исчезновению объекта и возникновению его в пространстве и даже в другом времени. Возможно эти механизмы и объясняют туннельный эффект, позволяющий разрешить парадокс Зенона «Стрела».
Ещё более необычными, но открывающими новые воззрения на природу пространства и времени, а также и движение, выглядят физические представления о нефундаментальности собственно пространства и времени. Пространство с этой точки зрения носит эмерджентный характер и порождается другой реальностью. В теории петлевой гравитации, альтернативной теории суперструн, пространство и время состоят из дискретных компонентов, называемых «кусками или атомами пространства-времени». При этом атомы пространства-времени объединены в сеть, соединяющую их одномерными и двухмерными поверхностями. Окружающее нас пространство выглядит как трёхмерный континуум, но на самом деле упаковано и пересекается атомами пространства-времени. Согласно струнной теории, пространство возникает из, казалось бы, несвязанной системы в виде квантовой запутанности подобно тому, как на дороге образуются пробки, благодаря коллективному решению водителей. Сами автомобили не есть движение, оно порождается движением автомобилей.
Под запутанностью понимается взаимодействие объектов, при котором между ними возникает взаимосвязь, сохраняющаяся, пока они изолированы от остального мира, и находятся независимо далеко друг от друга. Эйнштейн называл это «жутким действием на расстоянии».
Именно запутанность обеспечивает удержание пространства и не даёт рассыпаться на отдельные фрагменты [7]. Так, непрерывность и связанность обеспечивают единство и основу пространственно-временного континуума. Если разрушить запутанность, то пространство развалится, и мир исчезнет. Следовательно, само пространство возникает из основополагающего квантового явления. С другой стороны, появление пространства и времени больше похоже на коллективное поведение песчинок песчаной дюны, формирующейся на ветру. Пространство-время происходит из квантов пространства-времени, которые как зёрна песка не демонстрируют свойств самой дюны. Согласно теории суперструн и петлевой гравитации, пространство и время производятся более фундаментальной реальностью.
Данные подходы не являются единственными. Наиболее продуктивной является теория голографической Вселенной, согласно которой объекты возникают в результате постоянной проекции, своего рода «проявления» из другой двухмерной Вселенной, имеющей голографическую природу. Данный подход позволяет объяснить квантовый эффект запутанности и целостности, в том числе самого пространства. На уровне этой первичной реальности действует принцип «всё во всём», где каждая часть воспроизводит структуру целого, в том числе это относится и к самому пространству, демонстрируя инвариантность относительно масштабирования. Трансляция, своего рода проекция этой фундаментальной реальности, постоянно порождает пространство-время и объекты нашей Вселенной. Задача науки исследовать механизмы трансляции и физические способы воздействия на неё. Апории Зенона, открывшие парадоксы пространства-времени и движения привели к фантастическим теориям и поставили вопрос, насколько иллюзорна наша реальность, размышления над которым и способствовали развитию физики.
Играет ли Бог в кости?
Вопрос заключается в том, что либо объективная реальность это во многом следствие генерации случайных процессов, либо это наше незнание механизмов её порождающих. Особенностью случайности является её вероятностная природа и непредсказуемость в конкретных реализациях. Но что тогда есть реальность? Имеет ли она вероятностную природу, или Бог не знает результаты своей деятельности, поскольку Он играет в кости. Значит в действительности или не всё подконтрольно Богу, или природа случайности заключается всего лишь в нашем незнании.
Эти две сформулированные философские концепции являлись предметом спора выдающихся физиков XX века Альберта Эйнштейна и Нильса Бора о природе микромира. Бор считал, что микромир имеет вероятностную природу и объективный характер. Эйнштейн, напротив, полагал, что за фасадом случайности скрываются фундаментальные закономерные процессы, где никакая непредсказуемость существовать не может.
Спор двух гениев во второй половине XX века обрёл научно-техническую возможность выяснить, какая из этих кардинальных позиций верная. Джон Стюарт Белл сформулировал теорию скрытых параметров, позволяющую избежать схоластики и экспериментально проверить данные концепции. Французский физик Ален Аспе (Alain Aspect) и его последователи осуществили эксперименты, которые позволили установить истинность этих позиций. Если прав Эйнштейн, то степень скоррелированности процессов в микромире имеет меньше значение, если оно высокое, то прав Бор.
Два фотона, генерируемые из одного источника, находясь в состоянии суперпозиции, движутся в противоположных направлениях к поляризационным плёнкам. Вероятность успешно миновать плёнку для каждого составляет 50/50, однако в эксперименте либо они оба пролетают преграды, либо ни один из них. Третьего варианта не регистрировалось [8].
Результаты опыта Аспе и других исследователей подтвердили позицию Бора. Интересно, что на уровне макромира этот эксперимент выглядел бы следующим образом. Представим двух людей, сидящих спинами друг к другу и одновременно бросающих монеты. Если у них постоянно и одновременно выпадает, то орел, то решка – прав Бор. Если иначе, то прав Эйнштейн.
Тем не менее, не всё так однозначно. Существуют случайные процессы (правильнее их называть псевдослучайными), которые заключаются в генерации псевдослучайных чисел с помощью компьютерных алгоритмов, например, в программе Excel. Однако они не имеют никакой случайности, и всё же в конкретных последовательностях соответствуют ей. Это чёткие алгоритмы, математические формулы, в которых на самом деле нет случайности, но они проходят все тесты на её реализацию. Принимаются именно как случайные, как будто были получены в результате бросания игральных костей или оборота колеса рулетки. Эти числа имеют случайное распределение при определённых ограничениях, широко используются в науке и технике, но они детерминированы. Существует возможность, что и в природе есть некие скрытые механизмы, так же, как и в искусственной генерации псевдослучайных чисел, которых мы пока просто не знаем.
Кроме этого, есть голографическая модель реальности, согласно которой, всё, что существует в нашей Вселенной, есть проекция другой двухмерной Вселенной, имеющей голографическую природу, где случайности нет. Она имеет сложную квазипериодическую основу, состоящую из комплекса многих колебаний, но которые, в принципе, расчётны. И хаоса там нет и быть не может.
В таком случае наш мир возникает в результате трансляции параллельной Вселенной, и, зная первичную голографическую реальность, обладая алгоритмами реализации, можно понять, предсказать или устранить случайность. Тогда победа в споре остаётся за Эйнштейном, а значит, случайностей в нашем мире не существуют. Бог не играет в кости…
«Вещь в себе» и квантовомеханическая интерпретация реальности
Иммануил Кант был не только выдающимся философом, но и физиком, который на 100 с лишним лет предвосхитил основное положение физики микромира. Речь идёт о его понимании реальности и её взаимодействии с человеческим субъектом. Основные положения этого изложены в его труде «Критика чистого разума», вышедшего в свет в 1781 году.
И. Кант утверждал, что вещи существуют вне и независимо от человеческого субъекта, которые он называл «вещами в себе». На самом деле, кроме уже отмеченной, есть по крайней мере три трактовки, чем они являются. Это то, что остаётся непознанным в явлении, а также то, что лежит в трансцендентной сфере, находящейся за пределами нашего опыта и наконец то, что представляет идеал безусловного познания [9]. Почему же Кант считал, что «вещи в себе» непознаваемы?
Он исходил из положения о взаимодействии «вещей в себе» с чувственностью человеческого субъекта. Основными формами, по его мнению, являются пространство и время, а не ощущения и восприятие, т. е. пространство и время не есть атрибуты внешнего мира, присущие объектам. Поэтому «вещам в себе» нельзя приписывать их свойства. Они ими не обладают. Результат взаимодействия порождает явления, но они не открывают нам подлинного существования объектов внешнего мира. Кант приводит пример: «Предположим, что вы укололись иглой и почувствовали боль, но боль и игла – это разные вещи», т. е. формы чувственности, взаимодействующие с объектами, видоизменяют их свойства, и отделаться от этого невозможно.
При этом даже рациональные способности, такие как рассудок и разум, здесь не помогут. Они предназначены лишь для обработки материала явлений чувственной сферы и не могут выйти за её пределы. Если разум, оперирующий идеями и принципами, попытается выйти в трансцендентные сферы, то он запутается в противоречиях.
С чем же столкнулась физика на рубеже XX века, когда стала изучать микромир? Оказалось, что микрофизические объекты проявляли свойства волн или частиц в зависимости от того с какими приборами они взаимодействовали. Возник так называемый квантовый дуализм, некий кентавр, несущий в себе противоречие. Действительно, волна непрерывна, а частица дискретна. Как один и тот же объект может обладать такими двойственными свойствами?
Датский физик Нильс Бор вышел из этой ситуации, сформулировав принцип дополнительности, согласно которому всё зависит от взаимодействия микрообъекта с приборами. Приборы вмешиваются в состояния объекта и видоизменяют его. Отделаться от их влияния невозможно, поэтому разные приборы и по-разному проявляют эффект этого взаимодействия [10]. В связи с этим приписывать самим микрообъектам свойства либо волн, либо частиц неправомерно, они такими свойствами не обладают. На вопрос о том, а как же всё-таки микрообъекты выглядят без приборов, ответ Н. Бора был таков: «Мы не знаем, поскольку нет средств установить это». Ну и чем данное положение в принципе отличается от учения И. Канта о «вещах в себе»?
Формулировка немецким физиком Вернером Гейзенбергом принципа неопределённости ещё более запутало картину микрофизической реальности и привело к странным и во многом необъяснимым эффектам. Принцип неопределённости основывается на вероятностном понимании явлений микромира, в частности, пространственного и импульсного описания микрофизических явлений. Если, скажем, пространственное положение объекта не определено, то он может обнаруживать свою локализацию в определённой сфере, что ведёт к туннельному эффекту. Если поместить тонкое зеркало внутри световода, то фотоны пройдут через него и пронесут с собой информацию. Поскольку их положение не определено, то они туннелируются через препятствие. Долгое время считалось, что принципы дополнительности и неопределённости органично связаны между собой, однако в настоящее время установлено, что они имеют самостоятельное значение.
В 1936 году физики пришли к консенсусу, определившему, что оба подхода к определению микрообъектов имеют равноправный, хотя и противоречивый характер. Действительно, для описания волновых свойств используется уравнение Шрёдингера или преобразование Фурье, в то время как для описания частиц необходимо применять матричное исчисление. Математика оказывается совершенно различной.
Понимание того, что квантовые явления находятся в состоянии суперпозиции и демонстрирует их запутанность. Так, если микрообъекты находятся в этих состояниях и, даже если в пространстве они разделены огромными расстояниями, то воздействие на один объект приводит к мгновенному изменению параметров другого объекта. Это получило название принципа нелокальности. До сих пор более-менее внятного объяснения этому феномену нет, поскольку современная наука почему-то считает, что никакое физическое взаимодействие не может распространяться быстрее скорости света.
Возможно, физика XXI века сумеет разрешить эти парадоксы, и агностицизм И. Канта и Н. Бора будет преодолён. Если концепция голографической Вселенной окажется верной, то указанные противоречия могут быть легко объяснимы, и наконец удастся узнать, как выглядит микрофизическая реальность без приборов. Но это будет уже совсем другая наука.
Суперструны как предтеча новой теории Всего
Триумф физики заключается в создании теории относительности, описывающей физические процессы в макромире и квантовой механике, открывающей природу микромира. Несмотря на то, что эти концепции очень точны, попытка их объединения наталкивается на серьёзные методологические трудности, приводящие к парадоксам. Квантовая теория в лице стандартной модели универсальным образом описала и объединила три вида физических взаимодействий: электромагнитное, слабое и сильное ядерное, получив надёжное подтверждение в проведённых экспериментах. Между тем присоединить в рамках этой теории гравитацию до сих пор не удалось. В общей теории относительности гравитация рассматривается как кривизна пространства, в то же время в квантовой механике гравитационной волне как ряби пространства-времени должна соответствовать частица, называемая гравитоном. Построить объединённую теорию, базирующуюся на квантовой гравитации, до сих пор не удаётся. Дело в том, что на микроуровне из-за соотношения неопределённостей рождаются виртуальные частицы. В масштабах размеров меньше порядка 10-15 метра их энергии огромны, что приводит к резким деформациям, а по сути, к вспениванию пространства. В этих условиях математический аппарат квантовой механики перестаёт работать, поскольку в рамках данной теории предполагается, что пространство плоское, т. е. евклидово. Такое парадоксальное противоречие требует пересмотра одной из теорий или отказу от них обеих с заменой на концепцию с более фундаментальным пониманием реальности.
Перспектива в этих исследованиях появилась в 80-х годах прошлого века, когда М.Б. Грином была предложена так называемая теория суперструн. Согласно этой теории, пространство не рассматривалось как совокупность точек, что характерно для квантовомеханических представлений, а имело определённый размер, соответствующий предельному значению 10-35 метра. Другим важным концептуальным подходом явился отказ от трёхмерной пространственной метрики и постулирование многомерного пространства, в частности имеющего девять измерений и время. Более того, предполагалось, что эти пространственные измерения находятся в свёрнутом определённым способом состоянии. В момент Большого взрыва шесть измерений расширились и продолжают расширяться, что характерно и для сегодняшнего состояния Вселенной. В некоторых аспектах этой теории остальные шесть компактифицированных измерений, наоборот, продолжают сворачиваться. Вместо точечного представления частиц постулируется единый объект – суперструна, размеры которой составляют 10-35 метра, а сила натяжения, похожего на струну этого объекта, составляет 1019 Гэв или 1039 тонн. Спектр колебаний, взаимодействующей с пространством суперструны, порождает всё многообразие мира элементарных частиц и предсказывает, что если любое направление спина частицы рассматривать как отдельное с безмассовым состоянием, то всего будет 8064 безмассовых и 18 883 584 с наименьшей, отличной от нуля массой состояний. В теории суперструн гравитация действует в расширенном до девяти пространственных и одного временного измерения. Как и в теории относительности, движение совершается по кратчайшим траекториям, называемым геодезическими, только теперь это поверхность в десятимерном пространстве-времени [11].
В рамках этой теории рассматриваются два вида струн – открытых и замкнутых. Открытые струны имеют концы, с которыми связаны соответствующие заряды. Их колебания порождают безмассовые частицы со спином 1. Открытые струны могут сталкиваться своими концами, порождая третью струну. В то же время она может разорваться, породив пару новых открытых струн. Возможно соединение концов открытой струны, что приводит к образованию замкнутой струны. Колебания замкнутой струны включают безмассовый гравитон со спином 2. Любая теория с открытыми струнами предполагает наличие замкнутых струн, и теории с замкнутыми струнами не могут пренебречь гравитацией. Безмассовые состояния в теории суперструн содержат кроме гравитона частицы со спином 0 и 1/2, а также калибровочные частицы со спином 3/2, называемые гравитино. При энергиях меньше планковских безмассовые частицы тождественны объектам в квантовой теории супергравитации.
Важным моментом в теории суперструн является взаимодействие струнных объектов с пространством. Это приводит к топологическому многообразию пространственных форм. В пространстве могут возникать разрывы, нарушаться непрерывность, меняться связанность, что характеризуется возникновением «дырок». Если струна навьётся на тор, то её колебания проявятся как массивные магнитные монополи. Если теория относительности геометризировала физику, сведя гравитацию к метрическому показателю кривизны, то современная физика всё более топологизируется и требует учёта не только метрических свойств пространства, но и качественных, таких как размерность, связанность, ориентированность, включая всю палитру топологического многообразия.
В настоящее время теория суперструн критически пересматривается. Тому есть несколько причин. Прежде всего, отсутствует возможность её экспериментальной проверки, так как необходимые энергии не могут быть получены на современных ускорителях. Поэтому учёные рассматривают эту теорию как разработанный инструмент для дальнейших исследований. Так, по мнению американских исследователей, есть нечто более фундаментальное, из чего возникает пространство и время. В качестве таковой выдвигается идея параллельной голографической Вселенной, из двухмерного состояния которой в виде проекции, и возникает наш мир. Как отмечает Малдасена, для тестирования квантовой гравитации следует обратиться к космологии. Очевидно, именно там и присутствует то, что сегодня неизвестно и непонятно. В то же время лабораторные эксперименты могут пригодиться, если удастся найти удачные аналогии. А пока вопросы о том «Что есть пространство?» и «Что есть время?» остаются актуальными со времён древних греков.
Хаос и порядок. Прогнозирование и управление случайностями
Что понимается под хаосом, и какими свойствами он обладает? Это высокая степень энтропии, т. е. беспорядка, непредсказуемость, проявляющаяся в виде случайности. К явлениям неподдающимся точному предсказанию относятся атмосферные процессы, движение брошенной игральной кости, течение горной реки, биржевые колебания, броуновское движение.
Ранее считалось, что, обладая огромными вычислительными мощностями, можно предсказать поведение таких процессов. Эта точка зрения была обоснована французским математиком Лапласом. В свете классического детерминизма в этом мире случайностей не существует. Случайность – это наше незнание о процессах.
В начале XX века другой французский математик Пуанкаре опроверг эту точку зрения. Исследования показали – случайность есть объективное свойство природных процессов, и её нельзя устранить, накапливая информацию о системе. Оказалось, что и простые детерминированные системы могут порождать случайность, которую также нельзя устранить, наращивая информацию о них. Такие процессы назвали случайно-подобными. Они определены законами и правилами детерминирующих их изменений, которые не несут никакой случайности. Тем не менее быстрый рост неопределённости не допускает долговременного прогноза.
Необходимо отличать детерминированный хаос от стохастических процессов, связанных с массой действующих факторов. Эти различия, во-первых, заключаются в том, что детерминированные случайно-подобные процессы полностью воспроизводимы на любом этапе их реализации, в отличие от стохастических, которые таким свойством не обладают. Во-вторых, стохастические процессы сохраняют своё устойчивое поведение в противоположность детерминированным хаотическим. Например, представим себе расписание поездов. Воздействие стохастического фактора существенно не изменит структуры расписания, в отличие от случайно-подобного, который полностью его обрушит.
К моделям, порождающим хаотическое поведение, относят перемешивание, и кухонный миксер отлично выполняет эту операцию. Более мощный алгоритм генерации хаоса заключается в растяжении и сжатии траекторий в пространстве. Наглядно этот процесс демонстрирует «операция пекаря». Когда пекарь печёт пироги, для улучшения качества теста он разминает его с помощью скалки, а затем складывает. В результате близкие траектории разбегаются и становятся далёкими, а далёкие сближаются. При добавлении в тесто капли пищевого красителя уже через два десятка операций первоначальное пятно увеличит свою площадь в 20 млн раз, а его толщина сократится до молекулярного слоя. Краска полностью смешается с тестом. Хаос действует таким же образом. Складывание устраняет первоначальную информацию о системе, а растяжение стирает крупномасштабную, лишая нас возможности каких-либо предсказаний о её поведении [12].
И, несмотря на то, что хаос накладывает ограничения на возможность прогнозирования, он предполагает наличие связей там, где их ранее не подозревал никто. Хаос позволяет находить порядок в различных явлениях, таких как атмосферные фронты, капающий кран, физико-химические процессы.
Так что же такое порядок? В отличие от хаоса – это определённость, малая степень энтропии, периодичность, закономерность, наличие устойчивых связей между явлениями. В свете изложенного в самом хаосе есть порядок. Ещё в первой половине XX века английским математиком Рамсеем была доказана теорема, смысл которой стал понятен лишь в настоящее время – полный беспорядок невозможен. Чем больше мощность хаоса, тем больше в нём очагов порядка. Достаточно управляющими сигналами воздействовать на эти очаги, и станет возможно осуществить переход в упорядоченные состояния, чем сегодня и занимается новая наука – теория управляемого хаоса [13].
В настоящее время идёт поиск законов перехода хаоса в порядок. Если такие законы будут открыты, то нас ждёт научная революция, открывающая фантастические технологические возможности, по сравнению с которыми киборг Т-1000 в фильме «Терминатор-2: Судный день» покажется просто детской игрушкой.
Теория катастроф
В обыденной жизни часто происходят ситуации, которые сопровождаются резкими скачкообразными трансформациями, несмотря на привычные плавные движения. Классические методы математического анализа, основа которых была создана ещё Ньютоном и Лейбницем, ориентированные на исследования гладких плавных изменений, не справляются с описанием и прогнозированием подобных процессов.
Теоретические принципы, сформулированные классической наукой, базируются на парадигме того, что протекающие в нашей действительности процессы рассматриваются в виде постоянно меняющихся параметров. Однако большинство совершающихся трансформаций происходят скачкообразно, резкими качественными изменениями объектов и процессов: внезапное разрушение моста, закипание жидкости, возникновение тюремных бунтов, наступление биржевого кризиса или крушение самолётов. И такие кардинальные метаморфозы возникают обычно на фоне предшествующих весьма плавных изменений системы, когда их появлению вроде бы ничего не предвещает. Собственно катастрофой называется скачкообразные внезапные трансформации, возникающие в системе в виде её ответа на предшествующие плавные изменения внешних условий. При этом такие трансформации крайне плохо поддаются предсказаниям [14]. Однако в современной области математических знаний, которая носит название теории катастроф, разработаны методы, позволяющие в определённых условиях производить оценки подобных явлений.

Фазовое пространство Ляпунова. Изменение цвета показывает переход системы от упорядоченного состояния к хаотическому [15]
Французский математик Рене Том предложил называть теорией катастроф топологическую теорию динамических систем, используемую для оценки метаморфоз явлений природы, а также совокупность приложений теории особенностей, указав на наличие в подобных процессах структурной устойчивости. При установленных ограничениях переменных и параметров всё многообразие протекающих процессов можно свести всего к семи (!) классическим топологическим конструктам, к которым и будет стремиться поведение системы [16]. Анализируя топологические портреты, являющиеся особыми зонами в фазовом пространстве состояний, возможно установить границы бифуркационных множеств, при попадании в которые система станет совершать скачкообразные трансформации.
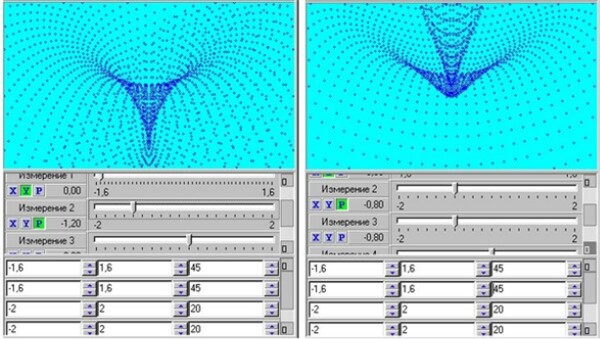
Двухмерные образы катастроф. Эллиптическая и параболическая омбилики
При стратификации успеваемости существуют довольно устойчивые группы, соответствующие как максимуму (отличники и близкие к ним студенты), так и слой студентов, соответствующий минимуму – имеющих неудовлетворительную успеваемость и занимающихся по нижней грани оценки удовлетворительно. Они находятся на разных листках топологической поверхности достижений. С точки зрения теории катастроф, в педагогическом процессе основные усилия по контролю знаний и обучению должны быть сконцентрированы на тех студентах, которые находятся в бифуркационной зоне. Так как студенты, имеющие посредственную успеваемость, могут скачком перейти в область хороших и отличных достижений, а хорошо успевающие студенты очень быстро выйти из опасной зоны бифуркации и обрести устойчивый ранг высоких оценок. Располагая данными IQ студентов, параметрами, обеспечивающими качество учебного процесса и используя методы теории катастроф, можно будет прогнозировать, и в определённых пределах более эффективно управлять качеством образования.
Практическое применение теории катастроф заключается в том, что огромное количество явлений, встречающихся в мире, она позволяет свести к очень ограниченному набору стандартных форм, и уже с их помощью провести количественные и качественные оценки динамично изменяющихся феноменов. Так как методы теории катастроф универсальны, они могут использоваться в сфере политики, экономики, управления, медицины, образования и т. п. Таким образом, научное познание получает новые эффективные инструменты для исследования феноменов реальности, до настоящего времени недоступных традиционным методикам и технологиям.
Фракталы в природе и организме человека
Статус математики в отношении природных процессов долгое время был не определён. В действительности нет точек, прямых линий, идеальных кругов и других фигур геометрии Евклида. С точки зрения здравого смысла, математика – это игра разума и задача познания с целью лишь описания явлений и их классификации. Поэтому древнегреческое знание не развило физику и естествознание. Создать физику и другие естественные науки – значит применить к действительности однородные точные математические и геометрические законы.
Только в Новое время Галилей, Ньютон и их последователи смогли обнаружить эти формы в механическом движении и простых механических системах. Тем не менее многие природные системы обладают огромной степенью сложности, несравнимой с использованием простых образов классической геометрии, поэтому их моделирование на такой основе оказывается невозможным. Действительно, как построить модели кроны деревьев, горного хребта, изрезанной береговой линии в объектах евклидовой геометрии? Как смоделировать сложные биологические объекты, обладающие многообразной конфигурацией, такие как нейронная сеть, система кровообращения, ацинусное строение легких, структура почек?
Столь сложной оказывается и динамическое поведение природных процессов, например, турбулентность, ритмы сердца и головного мозга. Для моделирования подобных явлений в конце XX века был создан новый тип геометрии, получившей название фрактальной. Термин фрактал был введён американским математиком Бенуа Мандельбротом в 1983 году, когда вышла его книга «Фрактальная геометрия природы». Фракталы – это, прежде всего, язык геометрии, но они выражаются в алгоритмах, наборах своего рода математических процедур, которые трансформируются в геометрические формы с помощью компьютеров. Основной принцип строения фрактала «всё во всём» или, как отмечают математики, он обладает инвариантной структурой относительно масштабирования. Это значит, что фрактал проявляет одинаковое строение на разных уровнях масштаба и, кроме этого, обладает дробной размерностью, в отличие от линий и площадей, имеющих целостное значение.
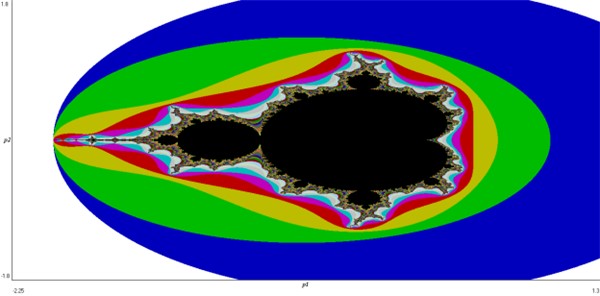
Множество Мандельброта. Построено в программе WinSet 3.0

Множество Жюлиа. Построено в программе WinSet 3.0
Существует два типа основных алгоритмов, каждый из которых имеет огромное многообразие комбинаций: линейные и нелинейные. Линейный алгоритм можно представить в виде копировальной машины, способной сжимать, т. е. уменьшать изображение, или увеличивать его. Таким образом, благодаря повторяющимся операциям, формируется образ объекта. Примером работы подобных алгоритмов служит изображение листа папоротника, треугольник Вацлава Серпинского, впервые описавшего этот объект ещё в 1916 году. Треугольник Серпинского обладает самоподобием, выражающемся в том, что каждая его часть, сколь малой она не была бы, воспроизводит структуру всего большого треугольника [17].
Другой тип фрактальных алгоритмов является нелинейным. Для этого используются итерационные циклы, имеющие степенные функции, иногда реализуемые в комплексных числах. Собственно такое изображение было получено Мандельбротом и получило название в его честь.
Несмотря на то, что эти функции достаточно просты, при проведении компьютером огромного количества операций с их помощью удаётся строить модели, в принципе, любых природных и биологических объектов. Поэтому фрактальная геометрия является языком объектов, и сомнения в её применимости к многообразию природы отпадают. Причём это не только просто воспроизведение природных структур, фрактальная геометрия даёт количественные характеристики тех или иных сложных конструктов, выраженные в понятиях фрактальной размерности, например, Хаусдорфа – Безиковича, Минковского и других [18].
Оказалось, что и динамические системы, демонстрирующие сложное хаотическое поведение при их моделировании, воспроизводят фрактальную структуру. К таковым можно отнести аттрактор Лоренца, возникающий в погодных явлениях, универсальность Фейгенбаума в турбулентности и даже в броуновском движении. Если при визуализации тех или иных процессов (для этого используется аппарат построения фазового пространства состояний) возникает фрактал, то, как правило, это след хаоса.
В человеческом организме много фракталоподобных структур, но чистые фракталы и в природе, и в биологических системах практически не встречаются. Как уже отмечалось, фракталы обладают самоподобием, или как говорят математики, они инвариантны относительно масштабирования, демонстрируя одинаковую структуру на разных уровнях рассмотрения. Фрактальные структуры, как правило, являются следом хаотических процессов. Поэтому динамический детерминированный хаос имеет тесную связь с этими объектами и проявляет себя в фазовом пространстве состояний в виде фрактальных или фракталоподобных структур.
Биологические системы имеют множество фракталоподобных образований [19]. К ним относятся структура кровеносных сосудов, нейронные сети, в том числе коры головного мозга. Фрактальное строение тонкого кишечника заметно увеличивает поверхность всасывания. Наиболее явно демонстрирует фрактальную природу структура дыхательных путей, которая обеспечивает более высокий уровень газообмена. Фракталоподобной структурой обладают сердечные артерии, что повышает устойчивость к повреждающим факторам, которые могут вызвать инфаркт миокарда. Несмотря на то, что анатомические и гистологические фрактальные структуры выполняют разные функции в организме, имеется нечто общее, что их объединяет. А именно, они обеспечивают запас прочности и устойчивости к различным действующим факторам, которые могут иметь и повреждающее воздействие.
Особый интерес представляет физиология и клиническая практика динамической работы сердца. Традиционно в физиологии и медицине сложилось представление о том, что ритм сокращений здорового сердца носит устойчивый регулярный характер, т. е. интервалы между сокращениями (ударами) сердца являются постоянными. Данные записи стандартного ЭКГ подтверждали эту точку зрения. Тем не менее тщательный анализ показал, что даже у здоровых людей ритм подвержен значительным колебаниям. На протяжении почти полувека господствовала концепция гомеостаза, согласно которой физиологические системы стремятся поддерживать постоянство своей среды и функций, возвращаясь, несмотря на флюктуации, к состоянию устойчивого равновесия.
Согласно этой концепции, вариабельность ритма сердца (ВРС) – это просто временные ответные реакции на воздействия внешних факторов. Многообразные влияния на ВРС, включая нейрогуморальные механизмы высших нервных центров, обуславливают нелинейный характер изменений ритма сердца, т. е. в основе феномена ВРС лежат случайные и случайно-подобные процессы, следовательно, наиболее точно и полно отображающими ВРС методами должны служить методы нелинейной динамики. Используя подход к вариабельности ритма сердца как к стохастическому феномену, следует пересмотреть методологию её изучения. В этом случае стандартные математические методы анализа оказываются ограниченными, так как являются неспособными оценивать явления, принципиально отличающиеся от традиционных линейных процессов. Поэтому становится понятным несостоятельность широко применяемых в клинике линейных математических методов и возникает необходимость в разработке новых способов оценки ВРС, которые бы позволили наиболее точно характеризовать это явление [20].
Совсем другая картина обнаруживается, если временная дискретизация ЭКГ в его стандартной форме 0,5–0,25 с заменяется на 1–4 мс. В результате ритм сердца приближается к хаотическому, а его визуализация в фазовом пространстве демонстрирует фрактальную природу. Применение методов оценки фрактальной размерности подобных образов устанавливает прямо противоположную парадигму. Именно здоровое сердце при такой дискретизации сигнала обнаруживает хаотичность своей работы. И наоборот «скатывание» в периодику и регулярность, проявляющееся в виде изменения фрактальных показателей, свидетельствует о надвигающейся катастрофе, что подтверждается в современных клинических исследованиях.
Новая парадигма утверждает, что нерегулярность, непредсказуемость, хаотичность являются характеристиками здоровья, а снижение изменчивости, потеря хаотичности, возникновение выраженной периодичности служат признаками надвигающейся или уже существующей патологии.
Рождение НЕ́ЧТО из НИЧТО́. Как из хаоса возникает порядок
Возможно ли, что дверь в закрытой комнате без внешних воздействий загорится сама собой, или в пирамиде самозаточится лезвие бритвы? Современная наука может утвердительно ответить на эти вопросы.
При комнатной температуре молекулы воздуха (являющиеся метафорически твёрдыми и жёсткими шариками) находятся в беспорядочном движении, и именно поэтому они не оказывают существенного воздействия на объекты, находящиеся в помещении. Их траектории, как утверждает кинетическая теория, носят вероятностный характер, но всё же существует хоть и чудовищно малая возможность, что, когда движение станет упорядоченным и направленным, большая часть молекул (или они все) ринется потоком на дверь, что приведёт к её возгоранию вследствие кинетического удара.
Но как может самозаточиться лезвие в пирамиде, причём известно, что даже колонии микроорганизмов, находящиеся в её центре, практически не размножаются? А если предположить, что именно форма пирамиды при взаимодействии с движущимися частицами индуцирует расслоение хаотического движения и направляет часть этого потока на лезвие, которое затачивается вследствие механического воздействия?
Возникает резонный вопрос, существуют ли способы, позволяющие нарастить минимальные вероятности подобных реализаций, обойдя второй закон термодинамики и открыть условия перехода хаоса в порядок? Ещё в XIX веке были известны явления подобного рода – ячейки Бенара, когда вязкая жидкость под действием небольшого, но строго определённого количества тепла вместо того, чтобы случайным образом распределяться по поверхности, формировала сотовую структуру, обусловленную конвекционными потоками.
Для того чтобы понять всю сложность подобного рода переходов, необходимо напомнить смысл основных понятий, где под хаосом понимается высокая степень энтропии, беспорядочность, неопределённость, случайность и непредсказуемость. Напротив, под порядком понимается малая степень энтропии, определённость, периодичность, предсказуемость, наличие закономерностей.
Каким же образом первое способно перейти во второе? Системный подход, исследующий эту проблему, сформировался в науке в конце XX века, что привело к возникновению новой области междисциплинарных исследований, получившей название синергетики. Творцами этой науки являются И.Р. Пригожин и Г. Хакен, установившие некоторые условия таких переходов: наличие открытых систем, осуществляющих обмен информацией, веществом, энергией с внешней средой и имеющих избыток энергии в самой системе. Следует отметить приоритет отечественных учёных Б.П. Белоусова и А.М. Жаботинского, открывших периодические реакции в химических процессах, считавшиеся невозможными с точки зрения официальной науки 50-х годов XX века, поскольку постулировалось, что химические взаимодействия между молекулами носят беспорядочный характер [21]. И только когда Жаботинский построил математическую модель брюсселятора, соответствующую этой химической реакции, пришло признание существования не только периодических автоколебательных процессов, но и возникновения упорядоченных структур и спиральных волн в химии.
Возникшие теория динамических систем и её часть – нелинейная динамика (физика хаоса), установили наличие частичной расчётности в хаотических явлениях. Прежде всего, речь идёт о детерминированном хаосе, особых явлениях, вызываемых жёсткими определёнными факторами, самими по себе не несущими никакой случайности, тем не менее под воздействием которых, системы демонстрировали хаотическое поведение. Используя математический аппарат фазового пространства, удалось визуализировать поведение динамической системы, что привело к открытию странных аттракторов – зон, в которых осуществляется реализация хаотических процессов.
Аттракторы – это участки фазового пространства, куда стремятся траектории процессов. Странные аттракторы отвечают за поведение хаотических систем и имеют необычную геометрию. Они относятся к фракталам, демонстрирующим одинаковое строение на разных уровнях масштаба, и в перспективе способным послужить основой для исследования управления перехода от хаоса к порядку.

3D визуализация множества Мандельброта, одного из самых сложных объектов фрактальной геометрии. Построено в программе WinSet 3.0 [22]
Особо следует отметить работу английского математика Рамсея, доказавшего теорему, согласно которой даже в хаосе есть порядок, и хотя он очень «хрупок», но он существует и чем больше мощность хаоса, тем больше в нём элементов порядка [23]. Наши древние предки распознали в созвездиях образы животных и людей, так появились знаки Зодиака. Современный человек видит в созвездиях правильные геометрические фигуры, которые в принципе не могли бы возникнуть, так как распределение звёзд в Галактике имеет случайный характер. Данные формы и представляют собой следствие теоремы Рамсея, поскольку количество звёзд, находящихся в случайном движении составляет огромное множество (по некоторым оценкам 200 млрд). Этого вполне достаточно для возникновения элементов порядка, чем и являются на самом деле данные структуры. Следствие теоремы Рамсея может послужить основой для наращивания порядка не только в детерминированном хаосе, но и в стохастических системах, где действует огромное количество факторов.
А что же происходит в космосе? Почему-то никто не обращает внимание на то, что термоядерные процессы, протекающие в звёздах, приводят к усложнениям. Ведь в звёздах из простейшего атома водорода синтезируются все сложные элементы периодической системы. Жизнь и человечество являются продуктами жизнедеятельности этих объектов, если бы их не было, то не было бы атомов, сложных соединений, в том числе органических, из которых состоит белковая жизнь. До сих пор современной науке не понятен феномен возникновения живой системы, являющейся сверхупорядоченной, устойчивой, самоорганизующейся и самовоспроизводящейся. Остаётся только надеяться, что наука ближайшего будущего будет способна ответить на эти вопросы.
Возникновение НИЧТО́ из НЕ́ЧТО. Переход от периодических и упорядоченных процессов к хаосу
В нашем мире присутствует как хаос, так и порядок. Значительная часть действительности во Вселенной представлена периодическими и квазипериодическими (сложными периодическими) процессами. Вопрос, насколько они обладают устойчивостью в различные моменты времени, имеет далеко нетривиальное значение.
Взять хотя бы Солнечную систему. Планеты движутся вокруг нашей звезды по орбитам близким к круговым, их положение в каждый момент времени расчётно и периодично. Несмотря на достижения небесной механики, существующей более двухсот лет, вопрос об устойчивости Солнечной системы всё ещё не решён. Останется ли наша планета Земля на своей орбите или упадёт на Солнце, улетит в дальний космос, столкнётся с другими планетами, не имеет ясности до сих пор. Отсутствует однозначное понимание и механизмов образования Солнечной системы. Так, согласно одной из моделей, она сразу в момент своего возникновения была таковой. Другой подход делает акцент на сложную эволюцию этой системы, и он, конечно, является более предпочтительным.
Возможны ли переходы от периодичности к хаотичности, существуют ли механизмы, обеспечивающие такую трансформацию? Возникшая в конце века новая область научного знания, получившая название нелинейной динамики, установила три основных сценария перехода к хаосу.
Первый, это последовательный каскад бифуркаций (изменение, раздвоение, удвоение) периода цикла (сценарий Фейгенбаума), возникающий под действием параметра, превышающего критическое значение [24]. В результате последовательности бифуркаций происходит мягкое возникновение хаотических траекторий, наряду с которыми существуют и окна периодичности. Было доказано, что из существования отображения в фазовом пространстве состояний (визуализаций) цикла периода 3 возникает хаотическая последовательность. Поэтому Т. Ли и Дж. Йорк назвали свою работу «Период три рождает хаос» [25]. Однако ни в работах Шарковского, установившего упорядоченные циклы (порядок Шарковского), ни в работах Ли-Йорка ничего не говорится об устойчивости циклов и размеров окон периодичности. Реализация сценария Фейгенбаума, благодаря своей универсальности, наблюдается во многих процессах от конвекции жидкости, находящейся в тепловом потоке переходящим в состояние турбулентности, до колебаний цен акций фондового рынка.
Второй – является жёстким переходом к хаосу всего через одну бифуркацию (сценарий Помо-Манневиля) [26]. Данный скачок сопровождается явлениями перемежаемости, заключающейся в том, что происходит чередование почти регулярных колебаний с зонами хаотического поведения. Это имеет огромное значение в понимании природных процессов, связанных с возникновением турбулентности. Происходит качественная перестройка в фазовом пространстве состояний, получившая название кризисов, в результате чего возникает хаос.
Третий – включает переходы к хаосу через различные квазипериодические процессы (сценарий Рюэля-Такенса) [27]. Согласно этому сценарию, переход к хаотическому поведению совершается после появления третьей частоты в двухчастотном квазипериодическом процессе. Тем не менее возможно возникновение хаоса и в двухчастотном режиме через разрушение квазипериодичности.
Необходимо отметить, что допустимы сложные комбинации представленных сценариев. Особый вариант возникновения хаоса осуществляется через явление резонанса, для которого характерно совпадение частот взаимодействующих процессов. Параметрический резонанс, как правило, приводит к резкому усилению колебаний, и при определённых условиях возможна их трансформация в хаотические и непредсказуемые состояния. Можно привести пример флаттера, резонансного воздействия в авиастроении, когда авиация вышла на субзвуковые скорости, а также разрушение ракетоносителя Королевской техники в результате резонанса колебаний работающих двигателей.
Возникшая в конце XX века теория катастроф, смогла объяснить и рассчитать скачкообразные переходы или метаморфозы как в природе, так и в любых сферах бытия, связанных с потерей устойчивости и упорядоченности. Действительно, внезапно закипает вода, вспыхивают бунты в тюрьмах, разрушается кристаллическая решетка вещества, а лишняя соломинка ломает спину верблюда. Причём никаким резким воздействиям эти объекты не подвергались. Их состояния плавно менялись, как и в предшествующие моменты времени, и ничто не предвещало катастрофу – резкое изменение в структуре или поведении системы. Основоположники теории катастроф Том, Зиман и Уитни выделили семь типов топологических конструктов или фазовых портретов, попадая в которые и пересекая бифуркационные зоны, система теряет устойчивость и разрушается. В результате возникает неупорядоченность вплоть до хаоса [28].
Возможен и обратный процесс, и это получило название бимодальности, где всё зависит от истории изменения. Установлено, что если количество воздействующих параметров не превышает пять, а переменных изменений два, то существует семь типов бифуркационных множеств, вычислив которые, и имея мониторинг движения, можно управлять состоянием системы, не допуская катастрофических явлений. Математика универсальна, и в настоящее время методы теории катастроф применяются уже практически во всех сферах реальности от физики твёрдого тела до психологии, экономики и политтехнологий.
Что первично хаос или порядок? Миры, где есть только что-то одно
Если рассматривать нашу Вселенную, то можно констатировать, что в этом мире преобладает случайность. Действительно, распределение звёзд в галактиках, расположение самих галактик, пылевых облаков, строение нейронной сети головного мозга, в чём-то напоминающее галактические распределения, всё это согласуется со вторым законом термодинамики, который утверждает возрастание энтропии как меры беспорядка, становящейся максимальной при равновероятностных состояниях. Хаос доминирует в нашем мире.
Тем не менее во Вселенной существуют и обратные процессы, стремящиеся к упорядоченности и усложнению. В звёздах протекают термоядерные реакции, в результате которых из простого элемента – водорода синтезируются все сложные атомы. Планеты вращаются вокруг звёзд, которые в свою очередь вращаются вокруг галактических ядер. К примеру, для нашего Солнца вместе с планетной системой такой цикл по разным оценкам составляет 220–240 млн лет и называется галактическим годом. Даже в химических реакциях присутствуют периодические и автоколебательные процессы, возникают явления самоорганизации. Наконец биологическая жизнь есть мощное антиэнтропийное явление, само возникновение которой с точки зрения современной науки имеет почти нулевую вероятность (единица, делённая на 201820). Но вопреки этому она существует и, согласно некоторым гипотезам, достаточно распространена во Вселенной [29].
В нашем мире присутствуют как случайность, беспорядочность, так и упорядоченность, и усложнение. Так что же первично, хаос или порядок? Для ответа на этот вопрос, необходимо выяснить в каком виде существует первичная реальность, и от какого критерия зависит наличие в ней либо хаоса, либо порядка.
Развитие топологии (науки о пространстве) позволило установить глобальный параметр, определяющий характер этих процессов в действительности – размерность пространства. Пространство может иметь любую размерность вплоть до N. И это ни метафора, и ни выверт математической мысли. Так, пространство нашей Вселенной имеет девять измерений, шесть из которых свёрнуты и образуют сложный топологический конструкт [30]. Они обнаруживают себя на планковском уровне масштаба, составляющим 10-35 м, в то время как трёхмерное пространство в момент Большого взрыва претерпело инфляцию (раздувание) и продолжает расширяться, это макро- и мегамир, в котором мы живём. Топологией установлено, что если размерность пространства меньше 3, например, 2 (плоскость) или 1 (линия), то в этих мирах хаос невозможен и случайностей не существует. Тогда как в пространстве размерности 3 присутствует и хаос, и порядок. Но, если пространство во Вселенной имеет больше трёх размерностей, например, 4, 5…N, то в этих Вселенных царит хаос, а периодика невозможна, впрочем, как и усложнение. Даже атомы здесь отсутствуют, это миры элементарных частиц и случайностей.
Идеи голографической и Мультивселенной, в частности: работы Бома, Малдасены, Хоофта предполагают, что наш мир является проекцией голографической двухмерной параллельной Вселенной, где существуют только квазипериодические процессы, а случайностей и хаоса не существует. Они возникают в результате трансляции этой голографической основы в нашу девятимерную Вселенную. Следовательно, первичная реальность носит квазипериодический характер и существует в виде голографической целостности.
Таким образом, порядок первичен, поэтому и реализуются антиэнтропийные процессы, базирующиеся на первичной основе параллельной реальности. И, несмотря на глобальную тенденцию энтропийной направленности, в нашей Вселенной присутствует локальная негэнтропийная реализация. Открытие условий, законов и механизмов этих процессов может реализовать фантастический вариант входа в первичную реальность, позволит научиться управлять её основой, что может изменить мир нашей Вселенной и нас самих.
Поразительно, но, по оценкам космологов, количество параллельных Вселенных может составлять огромное число – 10500. Однако, вероятно, только некоторые из них, могут оказывать на нас существенное влияние, а в настоящее время речь идёт о воздействии лишь одной – голографической Вселенной.
Жизнь как неслучайное явление. Информационный подход
Энтропийные явления царствуют в нашем мире. Информация в термодинамике определяется как обратная энтропия, т. е. выступает как мера упорядоченности. Если взглянуть на нашу земную форму жизни с точки зрения этого подхода, поражает огромная информационная ёмкость живой системы. Ведь даже самый простой микроорганизм на Земле имеет почти нулевую вероятность возникновения (1:201820). Каким образом в нашей Вселенной могла возникнуть и существовать такая сложнейшая система?
Возможно, решение этого вопроса заключается в единообразной трактовке самого понятия информации. Между тем общей теории информации не существует, это дело ближайшего будущего, на данный момент имеется несколько принципиально разных концепций, трактующих данный феномен. Наибольшее распространение получил вероятностный подход, сформулированный Хартли и Шенноном. С их точки зрения информация выступает как мера уменьшения неопределённости в наступлении статистических событий. Подход Шеннона является более широким по сравнению с Хартли, так как включает разновероятностные события. Он может быть использован для выяснения разницы мер структур, имеющих вероятностные характеристики, и определения меры детерминированности, следовательно, апостериорной (полученной в результате опыта) информации. В качестве эталона выступает полный беспорядок, для которого характерна предельно высокая степень энтропии.
Существуют также трактовки информации как разности мер структур, но не имеющих вероятностную природу, а задаваемых в различных алгебрах [31].
В рамках шенноновского понимания информации Винером была заложена основа кибернетического подхода, наиболее близкая к пониманию функционирования живой материи. Им было сформулировано два важных положения: первое, информация не существует без своего носителя, по отношению к которому она инвариантна, и второе, она представлена в сигнальной форме и имеет кодовый характер. Иными словами, информация есть выражение порядка организованных сигналов, являющихся отображением источника. Отсюда пришла идея генетического кода как основы биологических процессов. Был открыт универсальный носитель генетической информации – ДНК, а также РНК, которая содержится в некоторых вирусах. Именно эта концепция лежит в основе понимания сущности живого.
Имеется и другой подход, рассматривающий информацию как меру комплексности (сложности) объектов. В рамках идей конструктивной математики, согласно которой все объекты являются построенными (сконструированными), возникла алгоритмическая концепция, сформулированная отечественным учёным А.Н. Колмогоровым. В ней информация определяется как минимальная длина компьютерной программы, с помощью которой этот объект был построен. Например, если мы возьмём числовой ряд 1.2.3.4.5…N, то для построения любого члена ряда нам понадобится всего один оператор, так как следующий член ряда возникает после прибавления к предыдущему единицы. Иначе говоря, есть одна формула, с помощью которой он строится и, следовательно, такой ряд как математический объект обладает малой информационной ёмкостью. А вот если взять набор случайных чисел, которые не имеют компактного алгоритма описания, то тогда, сколько имеется этих чисел, столько и потребуется операторов для их представления, и информационное содержание такого объекта будет громадно, а он сам сверхсложен.
Некоторые учёные рассматривают хаос как сверхпорядок, поскольку он является сверхсложным. Наверное, неслучайно хаотические структуры, являющиеся фракталами, буквально пронизывают ткани живых организмов, вырастая из хаосогенных механизмов. И это требует переоценки даже основных понятий нормы и патологии в таких, казалось бы, классических науках, как биология и медицина.
Особый подход к пониманию информации был сформулирован отечественным учёным К.А. Валиевым, где информация определяется как изменение состояний системы. Он является более универсальным, поскольку количество состояний определяет информационную ёмкость, а их изменения – переработку информации. Тогда получают своё логическое объяснения такие объекты, как прионы, не имеющие ДНК и РНК, а также нанобактерии, представляющие собой кристаллическую форму жизни. Возможно, мы просто не там ищем жизнь в космосе. Иные её формы могут находиться у нас на Земле буквально под ногами. В принципе, на возникновение жизни в космосе могло сказаться и влияние параллельной голографической Вселенной. Ведь в этой Вселенной, имеющей двухмерные пространственные параметры, не существует случайностей, есть лишь сложные периодические процессы, а жизнь тоже по-своему периодична.