Уродливая Вселенная. Как поиски красоты заводят физиков в тупик - читать онлайн

Откуда мы пришли

В школе я ненавидела историю, но с тех пор осознала целесообразность цитирования умерших людей для обоснования своих суждений. Я даже не притязаю на то, чтобы дать вам экскурс в историю роли красоты в науке, поскольку на самом деле я больше интересуюсь будущим, чем прошлым, и к тому же другие этим уже занимались ⁹. Однако, если мы хотим увидеть, как физика изменилась, мне нужно рассказать вам, какой она была.

До конца XIX века ученым было довольно привычно считать красоту природы за признак божественности. Хотя они искали – и находили – объяснения, которые прежде были в ведении Церкви, неизъяснимая гармония, раскрываемая законами природы, обнадеживала верующих в том, что наука не представляет риска для сверхъестественного.

Примерно на рубеже веков, когда наука отделилась от религии и стала более профессионализированной, ее приверженцы перестали приписывать красоту законов природы божественному влиянию. Они изумлялись благозвучию, царящему в законах, что управляют Вселенной, но вопрос интерпретации оставляли открытым или по меньшей мере отмечали собственные верования как личное мнение.

В XX веке эстетическая привлекательность трансформировалась из приятного бонуса научных теорий в главного советчика при их построении, пока в конце концов эстетические принципы не переросли в математический критерий. Сегодня мы больше не раздумываем над аргументами о красоте – их ненаучное происхождение «затерялось в математике».

Среди первых ученых, сформулировавших количественные законы природы, был немецкий математик и астроном Иоганн Кеплер (1571–1630), работавший под сильным влиянием религиозных убеждений. У Кеплера была модель Солнечной системы, в которой известные тогда планеты – Меркурий, Венера, Земля, Марс, Юпитер и Сатурн – вращались по круговым орбитам вокруг Солнца. Радиусы орбит определялись правильными многогранниками – платоновыми телами, – вставленными друг в друга, и полученные таким образом расстояния между планетами хорошо согласовывались с наблюдениями. Идея была привлекательной. Кеплер считал, что «совершеннейший из строителей… с необходимостью должен был создать творение, обладавшее безупречной красотой».

Благодаря таблицам, фиксировавшим точные положения планет, Кеплер позднее убедился, что его модель неверна, и сделал вывод, что планеты движутся вокруг Солнца по эллиптическим орбитам, а не круговым. Его новая идея тут же была встречена неодобрением – она не соответствовала эстетическому стандарту того времени.

В частности, Кеплера критиковал Галилео Галилей (1564–1642), веривший, что «только круговое движение естественно подобает естественным телам, составляющим Вселенную и приведенным в наилучшее расположение»¹⁰[9]. Другой астроном, Давид Фабрициус (1564–1617), возмущался: «Своими эллипсами вы уничтожили кругообразность и равномерность движений, что представляется мне тем нелепее, чем больше я об этом думаю…» Фабрициус, как и многие в то время, предпочитал корректировать орбиты планет «эпициклами», то есть круговыми движениями меньшего радиуса вокруг круговых же орбит. «Если бы вы только могли сохранить идеальную круговую орбиту и обосновать свою эллиптическую орбиту другими небольшими эпициклами, – писал Фабрициус Кеплеру, – было бы намного лучше»¹¹.

Но Кеплер был прав. Планеты действительно движутся вокруг Солнца по эллипсам.

После того как объективные данные вынудили его отказаться от безупречных многогранников, Кеплер, в более позднем возрасте, пришел к убеждению, что планеты при движении рождают музыку. В своем трактате «Гармония мира», изданном в 1619 году, он вывел, как звучит каждая из планет, и заключил, что «Земля поет ми-фа-ми». Это была не лучшая его работа. Однако кеплеровский анализ планетных орбит заложил основы для последующих исследований Исаака Ньютона (1643–1727), первого ученого, который строго использовал математику.

Ньютон верил в существование Бога, чье влияние видел в законах, которым подчиняется природа. В 1726 году он написал: «Такое изящнейшее соединение Солнца, планет и комет не могло произойти иначе, как по намерению и по власти могущественного и премудрого существа»¹²[10]. С момента их открытия ньютоновские законы движения и тяготения были радикально пересмотрены, но в качестве приближений остаются действующими и сегодня.

Ньютон и его современники без раздумий совмещали религию и науку – тогда это было общепринятой практикой. Вероятно, особенно к тому был склонен Готфрид Вильгельм Лейбниц (1646–1716), разработавший дифференциальное и интегральное исчисление примерно в то же время, что и Ньютон, но независимо от него. Лейбниц верил, что мир, который мы населяем, «наилучший из всех возможных миров», а все существующее зло необходимо. «Каждая вновь обретенная истина, каждый опыт или теорема – это новое зеркало, в котором отражается красота Бога»¹³. Лейбниц считал, что несовершенство мира «основывается только на том, что мы слишком мало знаем всеобщую гармонию Вселенной и скрытые основания деятельности Бога»¹⁴[11]. Иными словами, согласно Лейбницу, ужасное ужасно, поскольку мы не понимаем, что есть красота.

Аргумент Лейбница, как любят рассуждать философы и теологи, бесполезен без определения, что вообще означает «наилучший». Но сама идея, что наша Вселенная оптимальна в некотором смысле, закрепилась в науке и пробилась сквозь века. Как только она была выражена математически[12], она выросла в гиганта, на чьих плечах стоят все сегодняшние физические теории. Современные теории отличаются лишь тем, как они требуют от системы «наилучшего» поведения. Общая теория относительности Эйнштейна, например, может быть выведена из требования, чтобы искривление пространства-времени было как можно меньшим. Подобные методы существуют и для других взаимодействий. И до сих пор физики стараются найти всеобъемлющий принцип, в соответствии с которым наша Вселенная «наилучшая», – к этой проблеме мы вернемся позже.

Как мы сюда попали

По мере того как проходили столетия и математика становилась все эффективнее, отсылки к Богу в физике потихоньку сходили на нет или вплетались в сами законы природы. В конце XIX века Макс Планк (1858–1947) верил, что «святость непостижимого Божества как бы придает святость постижимым символам»[13]. Затем, когда XIX век перетек в XX, красота постепенно трансформировалась в руководящий принцип физиков-теоретиков, закристаллизовавшийся с развитием Стандартной модели.

Герман Вейль (1885–1955), математик, сделавший важный вклад в физику, даже и не думал оправдываться за свои не очень-то научные методы: «В своей работе я всегда пытаюсь объединить истину с красотой, но, когда мне приходилось выбирать одно или другое, я обычно выбирал красоту»¹⁵. Астрофизик Эдвард Артур Милн (1896–1950), авторитетный ученый в период разработки общей теории относительности, считал красоту «дорогой к знанию, а точнее единственным знанием, которым стоит обладать». В своем выступлении 1922 года в Клубе естественных наук Кембриджского университета он выражал недовольство изобилием неприглядных исследований:

Поль Дирак (1902–1984), нобелевский лауреат, в чью честь названо уравнение, пошел еще на шаг дальше и выдал инструкции: «Исследователь в своих усилиях выразить фундаментальные законы природы в математическом виде должен главным образом стремиться к математической красоте»¹⁷[14]. В другой раз, когда Дирака попросили кратко сформулировать свою философию физики, он подошел к доске и написал: «ФИЗИЧЕСКИЕ ЗАКОНЫ ДОЛЖНЫ ОБЛАДАТЬ МАТЕМАТИЧЕСКОЙ КРАСОТОЙ»¹⁸. Историк Хельге Крах завершил биографию Дирака следующим наблюдением: «…После 1935 года [ему], как правило, не удавалось достигать физических результатов непреходящей ценности. Не будет неуместным заметить, что принцип математической красоты направлял его мышление только в течение более позднего периода»¹⁹.

Альберт Эйнштейн (1879–1955), вообще не нуждающийся в представлении, довел себя до состояния, в котором верил, будто мышление само по себе способно раскрывать законы природы: «Я убежден, что посредством чисто математических конструкций мы можем найти те понятия и закономерные связи между ними, которые дадут нам ключ к пониманию явлений природы. <…> Поэтому я считаю в известном смысле оправданной веру древних в то, что чистое мышление в состоянии постигнуть реальность»²⁰[15]. Справедливости ради отметим, что ученый в иных случаях все же подчеркивал необходимость наблюдений.

Жюль Анри Пуанкаре (1854–1912), внесший большой вклад как в математику, так и в физику, но наиболее известный, пожалуй, благодаря своему открытию детерминированного хаоса, восхвалял практическое применение красоты: «Мы видим, таким образом, что поиски прекрасного приводят нас к тому же выбору, что и поиски полезного…»²¹[16] Пуанкаре считал «экономию мышления» (Denkökonomie – термин, введенный Эрнстом Махом) «источником как красоты, так и практической пользы». Человеческое чувство прекрасного, утверждал он, «играет роль… тонкого критерия», помогающего исследователю разработать хорошую теорию, и «эта гармония одновременно удовлетворяет нашим эстетическим потребностям и служит подспорьем для ума, который она поддерживает и которым руководит»²²[17].

Да и Вернер Гейзенберг (1901–1976), один из основателей квантовой механики, смело верил, что красота владеет истиной: «Когда сама природа подсказывает математические формы большой красоты и простоты… то поневоле начинаешь верить, что они “истинны”, то есть что они выражают реальные черты природы»²³[18]. Как вспоминает его жена:

Опасайтесь прогулок под луной с физиками-теоретиками – иногда восторженность берет над нами верх.

Из чего мы сделаны

В мою бытность подростком, в 1980-е годы, не много было научно-популярных книг о современной теоретической физике или, не дай бог, математике. Биографии умерших людей – вот где приходилось искать. Просматривая книги в библиотеке, я воображала себя физиком-теоретиком, который пыхтит трубкой и думает великие думы, устроившись в кожаном кресле и рассеянно поглаживая бороду. Что-то в этой картинке казалось мне неправильным. Но идея, что математика плюс мышление способны раскрыть тайны природы, произвела на меня неизгладимое впечатление. Если это навык, которому можно выучиться, я хотела этому выучиться.

Одной из немногих научно-популярных книг, освещавших современную физику, в 1980-х годах была «Пугающая симметрия» Энтони Зи ²⁵. Тогда и до сих пор профессор Калифорнийского университета в Санта-Барбаре, он писал: «Мои коллеги и я, мы интеллектуальные преемники Альберта Эйнштейна, нам приятно думать, что мы тоже ищем красоту». И Зи изложил программу: «В этом веке физики стали крайне дерзки. <…> Им уже мало просто объяснить то или другое явление, они преисполнились веры, что Природе внутренне присуща прекрасная простота».

Они не только «преисполнились веры» в красоту, но и изыскали способ выразить свою веру в математической форме. Как писал Зи, «физики выработали понятие симметрии как объективного критерия для оценки устройства Природы. Когда есть две теории, физики чувствуют, что более симметричная, как правило, является и более красивой. В глазах физика красота подразумевает симметрию».

Для физика симметрия – это организующий принцип, избавляющий от ненужного повторения. Любой тип регулярности, схожести или порядка может быть математически запечатлен как выражение симметрии. Наличие симметрии всегда изобличает избыточность и допускает упрощение. Следовательно, симметрии объясняют больше с меньшими затратами.

Например, вместо того чтобы объяснять вам, что небо чистое на западе, на востоке, на севере, на юге, на юго-западе и так далее, я просто могу сказать, что оно чистое в любом направлении. Эта независимость от направления есть вращательная симметрия, благодаря которой достаточно описать, как система выглядит в одном направлении, после чего добавить, что она такая же и во всех других. Выгода – меньшее количество слов или, как в наших теориях, меньшее число уравнений.

Симметрии, с которыми имеют дело физики, представляют собой более абстрактные версии этого простого примера – вроде вращений относительно нескольких осей во внутренних математических пространствах. Но все они работают одинаково: найдите преобразование, относительно которого законы природы остаются инвариантными, – и вы нашли симметрию. Подобным преобразованием симметрии может быть что угодно, для чего вы можете записать четкую процедуру, – сдвиг, отражение, поворот или любая другая операция, какую вы только можете придумать. Если эта операция не меняет законов природы – вы нашли симметрию. С ней вы экономите усилия, которые необходимо было бы затратить, чтобы объяснить, к каким изменениям ведет эта операция: вместо этого вы просто констатируете, что изменений нет. Это и есть «экономия мышления» Маха.

В физике мы используем много разных типов симметрии, но у них у всех есть одна общая черта: симметрия – очень сильный объединяющий принцип, поскольку объясняет, как вещи, некогда казавшиеся очень разными, на самом деле, связанные преобразованием симметрии, составляют одно целое. Часто, однако, непросто найти правильную симметрию, чтобы упростить большие объемы данных.

Самым ошеломительным успехом принципов симметрии было, вероятно, создание кварковой модели. С момента появления ускорителей в 1930-х годах физики соударяли частицы друг с другом со все возрастающей энергией. К середине 1940-х они достигли энергий, позволяющих прощупать структуру атомного ядра, – и количество частиц стало расти. Сначала были заряженные пионы и каоны. Затем нейтральный пион и нейтральный каон, первые дельта-резонансы, частица, прозванная «лямбда», заряженные сигма-частицы, ро-частицы, омега-мезон, эта-, К*– и фи-мезон – и это было только начало. Когда Леон Ледерман спросил Энрико Ферми, что тот думает о недавнем открытии частицы, названной К₂⁰, Ферми ответил: «Молодой человек, если бы я мог упомнить названия этих частиц, я стал бы ботаником»²⁶.

Всего физики детектировали сотни частиц, каждая из которых была нестабильной и быстро распадалась. Казалось, эти частицы никак друг с другом не связаны, и это шло вразрез с надеждой физиков на то, что законы природы будут упрощаться для более фундаментальных составляющих материи. К 1960-м годам главной исследовательской задачей стало вместить этот «зоопарк частиц» в целостную теорию.

Одним из наиболее популярных подходов в то время был следующий: попросту отказаться от желания получить объяснение и записывать свойства частиц в большую таблицу – матрицу рассеяния, или S-матрицу, – которая была самой противоположностью красоты и экономии. А затем пришел Марри Гелл-Манн. Он определил подходящие свойства частиц – названные гиперзарядом и изоспином, – и оказалось, что все частицы разделяются на симметричные группы, так называемые мультиплеты.

Позднее стало понятно: закономерности мультиплетов означают, что наблюдаемые частицы состоят из более мелких объектов, которые – по тогда еще не вполне понятным причинам – никогда не детектировались сами по себе, по отдельности. Гелл-Манн назвал эти более мелкие составляющие «кварками»[19]. Более легкие объединения – мезоны – состоят из двух кварков, а более тяжелые – барионы – из трех. (Все мезоны нестабильны. К барионам относятся нейтроны и протоны, образующие атомное ядро.)

Симметрия получающихся систем, будучи однажды раскрытой, бросается в глаза (рис. 1). Примечательно, что, когда Гелл-Манн предложил эту идею, некоторые мультиплеты все еще были неполны. И поэтому требования симметрии побудили его предсказать существование частиц, необходимых для «дозаполнения наборов», в частности существование бариона омега-минус. Позднее тот был найден со свойствами, вычисленными Гелл-Манном, и ученый в 1969 году был награжден Нобелевской премией. Красота одержала победу над неприглядностью, постмодернистским S-матричным подходом.

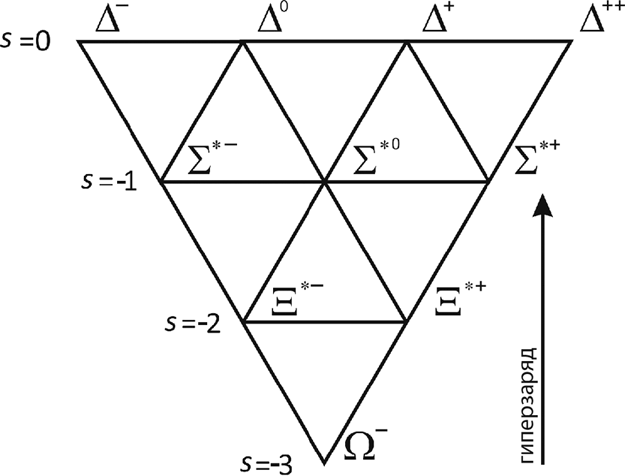
Рис. 1. Декуплет барионов – пример использования симметрий в теоретической физике. Гелл-Манн воспользовался его незавершенностью и предсказал существование частицы омега-минус (Ω^—) в нижней вершине.

Этот случай был только началом череды успехов на счету симметрий. Принципы симметрии также управляли работой – увенчавшейся опять-таки успехом – над объединением электромагнитного взаимодействия со слабым в электрослабое взаимодействие. Аналогично сильное взаимодействие было объяснено симметрией между элементарными частицами. Теперь и теории относительности Эйнштейна – специальная и общая – могли восприниматься как выражение требований симметрии.

Таким образом, современная вера в красоту как ориентир основывается на применении этого критерия в развитии Стандартной модели и общей теории относительности. Его часто оправдывают экспериментальной полезностью: замечено, что он работает, и кажется крайне целесообразным продолжать его использовать. Гелл-Манн сам сказал, что «в фундаментальной физике красивая или элегантная теория с большей вероятностью оказывается верна, чем неэлегантная теория»[20]. Ледерман, молодой человек, спрашивавший Ферми о частице К₂⁰, также впоследствии получил Нобелевскую премию и тоже обратился в веру поборников красоты: «Мы верим, что природа лучше всего описывается уравнениями как можно более простыми, красивыми, компактными и универсальными»²⁷.

Стивен Вайнберг, также удостоенный Нобелевской премии – за объединение электромагнитного и слабого взаимодействий, – любит проводить аналогию с коневодством: «[Коневод] смотрит на лошадь и говорит: “Прекрасная лошадь”. Хотя он или она может выражать чисто эстетическое чувство, я думаю, за этим стоит нечто большее. Коневод перевидал множество лошадей и по своему опыту работы с ними знает, что вот та лошадь, которая побеждает на скачках»²⁸.

Однако как опыт работы с лошадьми не помогает при конструировании гоночных машин, так и опыт теорий прошедшего столетия, вероятно, несильно поможет при создании теорий лучше прежних. Да и без оправдательных отсылок к опыту красота остается такой же субъективной, какой была всегда. Современные физики осознают это очевидное противоречие научному методу, однако же применение эстетических критериев стало широко распространенным. И чем дальше область исследований от экспериментальной проверки, тем больше учитывается эстетическая привлекательность соответствующих теорий.

В фундаментальной физике, которая настолько далека от экспериментальных испытаний, насколько только наука может быть, все еще оставаясь наукой, оценивание красоты особенно ярко выражено. Многие из моих коллег даже не пытаются отрицать, что уделяют больше внимания теориям, которые считают привлекательными. Их типичное предостережение против субъективных оценок неизменно сопровождается последующим «но» и отсылкой к распространенной практике.

Так, Фрэнк Вильчек, получивший в 2004 году вместе с Дэвидом Гроссом и Хью Дэвидом Политцером Нобелевскую премию за исследования сильного взаимодействия, пишет в своей книге «Красота физики», что «наше чувство прекрасного никак напрямую не приспособлено к фундаментальным работам Природы». Но: «Попробовав вкус красоты в сердце мира, мы жаждем большего. В этих поисках, я думаю, нет более многообещающего проводника, чем сама красота»²⁹[21].

Герард Хоофт, первым сформулировавший математический критерий естественности, который теперь направляет значительную часть исследований в теоретической физике элементарных частиц (и тоже удостоенный Нобелевской премии), предостерегает: «Красота – опасное понятие, поскольку она всегда может вводить людей в заблуждение. Если у вас есть теория, оказавшаяся красивее, чем вы исходно ожидали, это служит намеком на то, что все верно, что вы правы. Но никаких гарантий и в помине нет. На ваш взгляд, теория, положим, и красива, но она может быть просто ошибочной. И с этим ничего не поделаешь». Но: «Разумеется, когда мы читаем о новых теориях и видим, как они красивы и просты, у них есть немалое преимущество. Мы верим, что такие теории имеют гораздо больше шансов оказаться успешными»³⁰