Часть I
Глава 1. Десять историй о стратегии
НАЧНЕМ КНИГУ с десяти историй о стратегии, взятых из разных сфер жизни. Они дают первое представление о том, что такое оптимальный образ действий. Многие из вас, несомненно, попадали в подобные ситуации в повседневной жизни и находили правильное решение либо с помощью размышлений, либо методом проб и ошибок. Для кого-то некоторые из предложенных решений могут оказаться неожиданными, но мы приводим здесь эти примеры не для того, чтобы вас удивить. Наша цель – показать, что такие ситуации встречаются часто, что все они сводятся к определенному набору взаимосвязанных вопросов и что системный анализ этих ситуаций может принести свои плоды.
В следующих главах предлагаем рекомендации по созданию эффективных стратегий, основанных на этих концепциях. Отнеситесь к этим историям как к закуске перед главным блюдом: они предназначены для того, чтобы только возбудить ваш аппетит, а не насытить.
Хотите верьте, хотите нет, но мы предлагаем вам сыграть с нами в одну игру. Мы выбрали число от 1 до 100; ваша задача – угадать это число. Если вы правильно назовете его с первой попытки, мы заплатим вам 100 долларов.
Конечно же, мы вовсе не собираемся платить вам 100 долларов: это обошлось бы слишком дорого, особенно учитывая то, что мы намерены помочь вам с угадыванием числа. Но когда вы будете играть, мы хотим, чтобы вы думали, будто мы действительно заплатим вам эти деньги; а мы будем играть с вами на этих же условиях.
Вероятность угадать число с первой попытки достаточно низкая: от 1 до 100. Для того чтобы повысить ваши шансы на выигрыш, дадим вам пять попыток, а после каждой попытки будем говорить, какое число вы назвали – большее или меньшее. Разумеется, чем быстрее вы назовете правильное число, тем большим будет вознаграждение. Если вы угадаете число со второй попытки, получите 80 долларов. На третьей попытке ваше вознаграждение сокращается до 60 долларов, на четвертой – до 40, и на пятой оно составит 20 долларов. Если вам понадобится больше пяти попыток, это значит, что игра закончена и вы не получите ничего.
Готовы играть? Мы тоже готовы. Скорее всего, вы задаете себе вопрос: как можно играть с книгой? Это действительно сложно, но все-таки возможно. При желании можете зайти на сайт www.artofstrategy.net/ и сыграть в интерактивном режиме. А здесь мы можем предположить, как вы будете вести игру, и делать соответствующие ответные ходы.
Ваша первая догадка 50? Это самое часто встречающееся предположение и, к сожалению для вас, слишком большое число.
Возможно, ваша вторая попытка – 25? Назвав первым число 50, вторым большинство людей выбирают 25. Очень жаль, но это число слишком маленькое. На следующем этапе большинство людей называют число 37. К сожалению, 37 – тоже слишком мало. Как насчет 42? Снова слишком мало.
Давайте сделаем паузу, взглянем на ситуацию со стороны и проанализируем ее. У вас осталась пятая попытка – последний шанс выиграть у нас деньги. Вы знаете, что нужное число больше 42 и меньше 50. У вас есть семь вариантов: 43, 44, 45, 46, 47, 48 и 49. Какое из этих чисел вы выберете?
До настоящего момента вы пытались угадать число, выбирая среднее значение из оставшегося интервала. Это идеальная стратегия для игры, в которой число было выбрано случайным образом[8]. Вы получаете максимально возможную информацию из каждой своей догадки, поэтому сможете приблизиться к искомому числу за самое короткое время. Говорят, что генеральный директор Microsoft Стивен Балмер использовал эту игру в качестве испытания во время собеседований при приеме на работу. В понимании Балмера правильный ответ должен быть таким: 50, 25, 37, 42, …. Его в первую очередь интересовало, способен ли кандидат на вакантную должность решить эту задачу самым логичным и эффективным способом.
Мы предлагаем другое решение. В задаче Балмера число выбиралось произвольно, поэтому стратегия инженера «разделить совокупность на два и победить» была вполне уместной. Получение максимума информации из каждой догадки сводит к минимуму предполагаемое число догадок, а значит, позволяет выиграть наибольшее количество денег. Однако в нашем случае число выбиралось не в произвольном порядке. Помните, мы с самого начала предупредили, что будем играть так, как если бы действительно собирались платить вам деньги? Нам никто не возместит те суммы, которые гипотетически придется вам выплатить, значит, лучше сберечь их, чем отдавать вам. Поэтому мы сознательно выбрали число, которое вам будет трудно вычислить. Подумайте сами: разве было бы разумно с нашей стороны загадывать число 50? Это стоило бы нам целого состояния!
Главный урок теории игр заключается в том, что необходимо ставить себя на место другого игрока. Мы поставили себя на ваше место и предположили, что вы назовете сначала число 50, затем 25, затем 37 и 42. Понимание того, как вы будете играть, позволило существенно снизить вероятность того, что вы угадаете наше число, и тем самым сократить количество денег, которые нам пришлось бы выплачивать.
Объяснив это до завершения игры, мы дали вам фору. Теперь вы понимаете, в какую именно игру играете на самом деле. Каким будет ваше последнее предположение, за которое вы можете получить 20 долларов? Какое число вы выбираете?
Это число 49?
Поздравляем! Себя, а не вас. Вы снова попались в ловушку! Мы загадали число 48. На деле все эти рассуждения о выборе числа, которое трудно найти, выбирая среднее число из интервала, были направлены именно на то, чтобы ввести вас в заблуждение. Мы хотели, чтобы вы выбрали число 49, тем самым обезопасив наше число 48. Помните: наша задача – не отдать вам свои деньги.
Для того чтобы победить нас в этой игре, вы должны были опережать нас хотя бы на один шаг. Вам следовало размышлять так: «Они хотят, чтобы мы выбрали 49, значит, я выберу 48». Разумеется, если бы мы предположили, что вы настолько умны, мы выбрали бы число 47 или даже 49.
Смысл нашей с вами игры не в том, чтобы показать вам, какие мы хитрецы, а в том, чтобы наглядно проиллюстрировать, что именно делает любую ситуацию игрой: вы должны принимать во внимание цели и стратегии других игроков. Когда вы угадываете число, выбранное случайным образом, это число никто не пытается от вас спрятать. Следовательно, вы можете применить инженерный подход, выбрав среднее значение из интервала и тем самым получив лучший результат. Но если вы играете в реальную игру, нужно проанализировать, как будет действовать другой игрок и как его решения повлияют на вашу стратегию.
Должны признаться читателям в том, что смотрели реалити-шоу Survivor[9]. Мы ни за что не стали бы победителями на том острове. Если бы мы не сдались из-за мук голода, другие участники игры наверняка избавились бы от нас за то, что мы «умники». Однако нам было очень интересно попытаться предсказать, чем закончится игра. Для нас не стало неожиданностью, что невысокий нудист с плотным телосложением Ричард Хэтч перехитрил, обыграл и продержался дольше всех остальных участников, став первым победителем этого реалити-шоу на канале CBS и выиграв приз 1 миллион долларов. У него был особый дар: способность действовать стратегически и не выглядеть при этом стратегом.
Самый хитрый тактический ход Хэтч сделал в последнем эпизоде. В игре остались только три участника. Соперниками Ричарда были 72-летний бывший «морской котик» Руди Бош и 23-летний речной гид Келли Вигглсворт. Последнее испытание состояло в том, чтобы встать на опору и держаться рукой за идола иммунитета, стоящего в центре круга. Участник игры, простоявший дольше всех, выходил в финал. Важно и то, что победитель решал, кто из двух проигравших пройдет с ним в финал.
На первый взгляд может показаться, что в этом испытании главную роль играла физическая выносливость. Но давайте проанализируем ситуацию более внимательно. Все три игрока понимали, что наиболее вероятный победитель – Руди. Единственное, на что мог рассчитывать Ричард, – это выйти в финал вместе с Келли.
Существовали только две возможности добиться этого. Первая – Келли победит в этом испытании и выберет Ричарда. Вторая – Ричард победит и выберет Келли. Ричард мог рассчитывать на то, что Келли выберет именно его. Она осознавала, что Руди очень популярен среди участников игры и что для нее единственный шанс одержать победу состоит в том, чтобы выйти в финал с Ричардом.
Казалось, ситуация складывалась так, что кто бы ни выиграл в последнем испытании, Келли или Ричард, каждый из них выберет другого в качестве соперника. Следовательно, Ричард мог бы попытаться остаться в игре – по крайней мере до тех пор, пока Руди не сойдет с опоры. Единственная проблема состояла в том, что между Ричардом и Руди давно сложился союз. Если бы Ричард победил в испытании и не выбрал Руди, это восстановило бы Руди и всех его друзей против Ричарда. И это могло стоить Ричарду победы. Одна из характерных особенностей шоу Survivor состоит в том, что победителя определяют выбывшие из игры участники. Следовательно, каждый участник игры должен очень осмотрительно вести себя с соперниками.
С точки зрения Ричарда, последнее испытание могло развиваться по одному из трех сценариев.
• Побеждает Руди. Он выбирает Ричарда, но при этом у Руди больше шансов на победу.
• Побеждает Келли. Она достаточно умна, чтобы понимать: ее единственный шанс на победу – избавиться от Руди и бороться в финале с Ричардом.
• Побеждает Ричард. Если он выберет Руди, тот победит его в финале. Если он выберет Келли, она может победить его, поскольку Ричард потеряет поддержку Руди и его многочисленных друзей.
Сопоставив все возможные варианты развития событий, Ричард пришел к выводу, что для него лучше всего проиграть в данном испытании. Ему необходимо, чтобы Руди выбыл из игры, но будет лучше, если Келли сделает за него всю грязную работу. Самым умным шагом было бы сделать ставку на победу Келли в этом испытании. Она уже победила в трех из четырех предыдущих; кроме того, поскольку Келли, будучи гидом, проводила экскурсии на природе, она была в наилучшей физической форме.
Такой вариант развития событий давал Ричарду приятный бонус: отпадала необходимость стоять на опоре под жарким солнцем. В самом начале испытания ведущий шоу Джефф Пробст предложил ломтик апельсина тому, кто решит прекратить дальнейшую борьбу. Ричард сошел с опоры и получил апельсин.
Через 4 часа 11 минут Руди сделал неудачную попытку сменить положение, оторвался от идола иммунитета и проиграл испытание. Для участия в финале Келли выбрала Ричарда. Руди решил исход голосования, отдав свой голос в пользу Ричарда, и Ричард Хэтч оказался первым победителем реалити-шоу Survivor.
Если оценивать ситуацию в ретроспективе, этот расчет кажется достаточно простым. Но Ричард смог предвидеть все возможные варианты развития событий еще до того, как они произошли[10]. В главе 2 вы найдете ряд инструментов, которые помогут вам прогнозировать ход игры и даже дадут возможность попробовать свои силы в очередном сезоне реалити-шоу.
В этой книге мы часто делаем отступления, которые называем «задачами для тренировки мышления». В таких отступлениях рассматриваются более сложные элементы игры, которые мы обошли молчанием в основном тексте. Например, в приведенном примере Ричард мог бы немного подождать, чтобы увидеть, кто выйдет из игры первым. Если бы первой сошла с опоры Келли, Ричарду было бы более выгодно победить Руди и выбрать Келли, чем позволить Руди выиграть и бороться с ним в финале. Кроме того, Ричард мог бы подумать и о том, что Келли достаточно находчива, чтобы просчитать те же варианты и тоже первой выйти из игры. В следующих главах вы узнаете о том, как использовать системный подход к поиску способов достижения победы в игре. Наша конечная цель – помочь вам изменить свой подход к оценке стратегических ситуаций и осознать тот факт, что у вас далеко не всегда будет время для анализа всех возможных вариантов развития событий.
Действительно ли у спортсменов бывает «счастливая рука»? Порой создается впечатление, что Яо Мин[11] просто не способен не попасть мячом в корзину или что Сачин Тендулкар[12] не может не выиграть сотню в крикете. Спортивные комментаторы, наблюдающие за такими длинными периодами непрерывных успехов некоторых спортсменов, утверждают, что у них «счастливая рука». Однако профессора психологии Томас Гилович, Роберт Валлоне и Амос Тверски считают, что этот вывод не соответствует реальному положению дел[13]. Они утверждают, что, если бросать монету достаточно долго, рано или поздно она много раз подряд выпадет «орлом» либо «решкой». По мнению этих психологов, комментаторы, которым порой не о чем говорить, просто выбирают из длинного игрового сезона периоды успешной игры. Они наступают точно так же, как после целой серии подбрасываний монета выпадает одной стороной несколько раз подряд. Эти психологи предлагают более точный, научно обоснованный тест на примере игры в баскетбол. Они подсчитывают все случаи, когда определенный игрок попадает мячом в корзину, после чего вычисляют процент тех эпизодов, когда следующий бросок тоже оказывается удачным. Такие же расчеты делаются и для тех случаев, когда за попаданием следует промах. Говорить о «счастливой руке» можно только тогда, когда после попадания в корзину далее чаще следует попадание, а не промах.
Психологи провели этот тест среди игроков баскетбольной команды Philadelphia 76ers. Полученные результаты опровергли теорию «счастливой руки». Когда игрок делал удачный бросок, в следующий раз он чаще всего промахивался; когда он промахивался, следующий бросок чаще оказывался удачным. Именно такая закономерность наблюдалась даже у Эндрю Тоуни, имевшего репутацию игрока, способного сделать серию удачных бросков. Значит ли это, что мы должны говорить здесь о руке, действующей по принципу стробоскопа, как в проблесковом маяке, в котором свет то включается, то выключается?
Теория игр предлагает другое объяснение. Статистические данные говорят об отсутствии у игроков способности делать длинные серии удачных бросков, однако они и не опровергают возможность того, что игроки со «счастливой рукой» действительно могут так или иначе «подогреть» игру. Различие между серией удачных бросков и «счастливой рукой» возникает в силу взаимодействия между стратегией нападения и стратегией защиты. Предположим, у Эндрю Тоуни действительно «счастливая рука». Разумеется, в таком случае игроки команды-соперника начнут оттеснять его от мяча, что может снизить процент попаданий мяча в корзину.
И это еще не все. Когда защитники соперника фокусируются на Тоуни, один из его товарищей по команде остается без опеки и его шансы забросить мяч в корзину повышаются. Иными словами, «счастливая рука» Тоуни обеспечивает повышение командной результативности, хотя индивидуальная результативность самого Тоуни может снизиться. Таким образом, чтобы проверить, есть ли «счастливые руки» у игроков команды, нужно проанализировать периоды успешной игры команды в целом.
Подобный феномен наблюдается во многих командных видах спорта. В американском футболе блестящий раннинбек помогает своим товарищам по команде делать пасы вперед, а талантливый ресивер – продвигать мяч вперед, поскольку противник вынужден «опекать» звездных игроков. В 1986 году в финале Чемпионата мира по футболу звезда аргентинской команды Диего Марадона не забил ни одного гола, но его передачи через кольцо защитников команды Западной Германии обеспечили Аргентине два гола. Ценность звездного игрока нельзя оценивать только по его личной результативности; его вклад в повышение результативности других членов команды играет важнейшую роль, а статистические данные о числе голевых передач позволяют этот вклад оценить. В хоккее индивидуальная результативность игроков определяется в равной степени числом как голевых передач, так и забитых шайб.
Игрок может помочь даже самому себе, когда одна его «счастливая рука» поддерживает другую. Звездный игрок команды Cleveland Cavaliers Леброн Джеймс ест и пишет левой рукой, но броски в корзину предпочитает делать правой (хотя левой рукой он по-прежнему бросает мяч точнее). Защитники знают, что Леброн правша, поэтому стараются защищать свою корзину от бросков правой рукой. Но они не могут сосредоточиться только на этом, поскольку броски Леброна левой рукой слишком эффективны, чтобы оставлять их без защиты.
Что произойдет, если в период между сезонами Леброн поработает над улучшением бросков левой рукой? Защитники команды-соперника отреагируют на это, уделяя больше внимания прикрытию его бросков слева. В результате у Леброна появится больше возможностей для бросков правой рукой. В этом примере левая рука не только знает, что делает правая, но и помогает ей.
В развитие этой темы в главе 5 мы показываем, что, если левая рука сильнее, ее можно использовать даже реже, чем правую. Многие из вас наверняка поняли это на собственном опыте во время игры в теннис. Если у вас удар слева слабее, чем удар справа, соперники узнают об этом и будут чаще играть против вашей левой руки, но благодаря такой практике ваш удар слева улучшится. Когда ваши удары слева и справа станут в равной степени эффективными, соперники больше не смогут воспользоваться слабостью вашей левой руки. Вы начнете чаще использовать удар справа – в этом и есть истинное преимущество отработки удара слева.
После первых четырех заплывов в финале Кубка «Америки»[14] яхта Liberty со шкипером Деннисом Коннером вела со счетом 3:1 в серии заплывов на определение лучшей из семи яхт. Утром в день пятого заплыва на причал, где должна была пришвартоваться яхта Liberty, доставили ящики с шампанским. На яхте для зрителей жены членов экипажа Liberty, одетые в майки и шорты в красных, белых и голубых тонах, уже предвкушали, как их всех будут фотографировать, когда их мужья в очередной раз выиграют кубок, обладателем которого на протяжении 132 лет подряд оказывались Соединенные Штаты Америки[15]. Но этому не суждено было случиться.
На старте яхта Liberty получила 37 секунд преимущества, когда Australia II совершила фальстарт и поэтому вернулась на линию старта. Шкипер австралийской яхты Джон Бертран попытался наверстать упущенное, отклонившись от курса влево в надежде на удачную перемену ветра. Деннис Коннер решил оставить Liberty справа от курса. Но рискованный шаг Бертрана оправдал себя. Направление ветра сместилось на пять градусов в выгодную для Australia II сторону; в итоге эта яхта выиграла гонку, опередив Liberty на 1 минуту 47 секунд. Коннера раскритиковали за то, что он не последовал по тому же курсу, который взяла Australia II, это оказалось серьезной стратегической ошибкой. После еще двух заплывов яхта Australia II выиграла всю серию.
Парусная регата дает возможность проанализировать интересный обратный вариант стратегии следования за лидером. Как правило, лидирующий парусник копирует стратегию корабля, идущего вслед за ним. Когда отстающий парусник меняет курс, лидер делает то же самое. Лидер копирует действия отстающего, даже если его стратегия явно неэффективна. Почему? Потому что в парусном спорте – как и в бальных танцах – важна только победа. Если вы уже занимаете первое место, самый верный способ оставаться первым – имитировать действия тех, кто идет следом за вами[16].
Фондовые аналитики и составители экономических прогнозов тоже часто придерживаются стратегии подражания. Ведущие специалисты по составлению прогнозов заинтересованы в том, чтобы следовать за большинством и делать прогнозы, не противоречащие прогнозам других аналитиков: это снижает вероятность того, что люди изменят свое мнение о способностях этих специалистов. С другой стороны, новички часто применяют рискованные стратегии; они предсказывают либо резкий подъем, либо стремительное падение экономики. В большинстве случаев их выводы оказываются ошибочными, и о них все забывают. Тем не менее время от времени некоторые из них делают правильные прогнозы и благодаря этому становятся знаменитыми.
Конкуренция в сфере промышленности и технологий предлагает новые доказательства в пользу этой точки зрения. На рынке персональных компьютеров компания Dell известна скорее не своими инновациями, а способностью выводить унифицированные технологии на массовый рынок. В свое время большинство новых идей родились в Apple, Sun и других начинающих компаниях. Рискованные инновации – это их главный и, возможно, единственный шанс получить свою долю на рынке. Такая ситуация складывается не только на рынке высокотехнологичных продуктов. Компания Procter & Gamble, своего рода «Dell» на рынке подгузников, начала использовать на своих подгузниках изобретенные в Kimberly-Clark застежки-липучки и благодаря этому восстановила доминирующее положение на рынке.
Существует два способа двигаться вторым. Вы либо начинаете копировать действия лидера, как только он раскроет свой подход (как в парусной регате), либо ждете, когда станет ясно, успех или неудачу принесет этот подход (как в компьютерной сфере). В бизнесе ожидание – это более выгодный путь, поскольку в отличие от спорта конкуренция в бизнесе проходит не по принципу «победитель получает всё». Поэтому лидеры рынка не следуют за компаниями, неожиданно достигшими успеха, пока не убедятся в преимуществах их курса.
Когда католическая церковь потребовала от Мартина Лютера отказаться от своих выступлений против власти пап и соборов, он не стал отрекаться от своих убеждений: «Я не могу и не хочу ни от чего отрекаться, ибо неправоверно и неправедно делать что-либо против совести». Он не пошел на компромисс: «На том стою и не могу иначе»[17]. Непреклонность Лютера основывалась на убежденности в том, что его позиция ниспослана ему Богом. Там, где шла речь о праведности, не было места компромиссу. Стойкость Лютера повлекла за собой долгосрочные последствия: его выступления против папства положили начало протестантской Реформации и существенным изменениям в средневековой католической церкви.
Непреклонность помогла Шарлю де Голлю стать весьма влиятельным игроком на арене международных отношений. Его биограф Дон Кук сказал: «Де Голлю удалось добиться власти, не имея ничего, кроме незыблемых моральных принципов, интеллекта, личных качеств и ощущения собственного предназначения»[18]. Однако главной чертой Шарля де Голля была его непреклонность. Во время Второй мировой войны, будучи самопровозглашенным лидером побежденной и оккупированной страны, он сам организовал переговоры с Рузвельтом и Черчиллем. В 60-х годах его президентское «Нет!» несколько раз предотвращало вступление Франции в Европейское экономическое сообщество (ЕЭС).
Каким образом непреклонность Шарля де Голля обеспечивала ему сильную позицию на переговорах? Когда он занимал поистине несокрушимую позицию, у других участников переговоров оставались только два варианта – принять ее или отвергнуть. Например, именно де Голль выступил против вступления Англии в Европейское экономическое сообщество – в 1963-м, а затем в 1968 году. Другие страны были вынуждены либо принять его вето, либо разрушить ЕЭС. Де Голль тщательно взвешивал свою позицию, чтобы добиться ее принятия. Однако нередко это приводило к несправедливому распределению выгод в пользу Франции. Непреклонность де Голля лишала другую сторону возможности выдвинуть приемлемое для нее встречное предложение.
На практике это легче сказать, чем сделать, – по двум причинам. Первая связана с тем, что в большинстве случаев во время переговоров обсуждаются условия, не имеющие отношения к сиюминутным выгодам. Ощущение, что вы занимаете слишком корыстолюбивую позицию, может повлечь за собой нежелание других участников переговоров иметь с вами дело в будущем. Или же они займут на следующих переговорах более жесткую позицию, пытаясь не допустить возможных потерь. На личностном уровне нечестная победа может испортить деловые или даже личные отношения с другими людьми. На самом деле биограф Шарля де Голля Дэвид Шонбрун обвинил его в шовинизме: «В отношениях между людьми тот, кто сам никого не любит, редко бывает любим; тот, кто не умеет дружить, не имеет друзей. Именно поэтому неприятие де Голлем дружбы навредило Франции»[19]. То, что кажется компромиссом сейчас, может оказаться более эффективной стратегией в будущем.
Вторая проблема заключается в том, чтобы обрести необходимый уровень непреклонности. Мартин Лютер и Шарль де Голль выработали твердость благодаря личным качествам, но это дорого обходится. Несгибаемый характер нельзя включать и выключать по ситуации. Непреклонность ослабляет оппонента и вынуждает его пойти на уступки, однако с таким же успехом приводит к тому, что небольшие потери перерастают в серьезные проблемы.
Фердинанд де Лессепс был посредственным инженером, но обладал невероятной дальновидностью и решительностью. Он стал знаменитым благодаря строительству Суэцкого канала в условиях, в которых это казалось невозможным. Лессепс не признавал невозможного и по этой причине смог добиться своей цели. Впоследствии он попытался применить тот же метод при строительстве Панамского канала, но это закончилось катастрофой[20]. Пески Нила подчинились его воле, тропическая малярия – нет. Проблема Лессепса состоялась в том, что его жесткий характер не позволял ему признать поражение даже тогда, когда битва была проиграна.
Как достичь избирательной непреклонности? Здесь нет идеального решения, но существуют способы, с помощью которых можно выработать определенный курс и неуклонно ему следовать (это тема главы 7).
Синди Нэксон-Шехтер хотела сбросить вес. Она точно знала, что для этого нужно: меньше есть и больше двигаться. Она знала все о пищевой пирамиде и о скрытых калориях в напитках. Тем не менее ничто не помогало ей похудеть. После рождения второго ребенка она набрала почти 20 килограммов, и ей никак не удавалось от них избавиться.
Именно поэтому Синди приняла предложение канала ABC помочь ей похудеть. 9 декабря 2005 года она пришла в фотостудию, расположенную в районе Вест-Сайд на Манхэттене. Там ей предложили надеть бикини. Синди не надевала бикини с девяти лет, и теперь было не совсем подходящее время для того, чтобы сделать это снова.
Обстановка в фотостудии напоминала то, что разворачивается за кулисами во время подготовки к выпуску журнала Sports Illustrated с фотографиями супермоделей в купальных костюмах. Повсюду стояли осветительные приборы и фотоаппараты, а на Синди было только бикини цвета лайма. Продюсеры предусмотрительно установили в помещении скрытый обогреватель, чтобы Синди не мерзла. Щелк. Улыбка. Щелк. Улыбка. О чем, черт возьми, она думала? И снова щелк.
Если все пойдет так, как рассчитывает Синди, никто не увидит этих ее фотографий. Она заключила с ABC Primetime сделку: если Синди потеряет за два месяца семь килограммов, эти фотографии будут уничтожены. Но при этом ей никто не станет ничем помогать. Никакого тренера, никакого инструктора, никаких специальных диет. Она уже и без того знала, что ей делать. Все, что было нужно, – это дополнительная мотивация и повод для того, чтобы начать прямо сегодня, а не завтра.
Теперь у Синди появилась дополнительная мотивация. Если она не сбросит обещанного веса, канал АВС покажет ее фотографии и видео в прайм-тайм. Синди уже подписала разрешение на это, отказавшись от любых претензий в адрес телеканала.
Сбросить семь килограммов за два месяца – задача достижимая, но не такая уж и легкая. Впереди вырисовывалась серия праздничных вечеринок и рождественских ужинов. Синди не могла рисковать, откладывая поставленную задачу до Нового года. Она должна была начать сразу же.
Синди хорошо знала обо всех опасностях избыточного веса: повышенный риск диабета, острых сердечно-сосудистых заболеваний и даже смерти. Но этого все равно было недостаточно, чтобы напугать ее и заставить действовать. Чего Синди боялась больше всего – так это того, что ее бывший друг увидит ее в бикини на национальном телеканале. Вряд ли стоило рассчитывать на то, что он не будет смотреть это шоу. Если ему не скажет об этом сама Синди, это сделает ее лучшая подруга.
Лори Эдвардс не устраивал ни ее внешний вид, ни самочувствие. Не помогло и то, что она работала барменом в окружении горячих молодых парней двадцати с лишним лет. Не помогала ни диета Weight Watchers («Стражи веса»), ни South Beach («Южный берег»), ни Slim-Fast («Худеем быстро») – всего не перечислить. Лори двигалась не в том направлении, поэтому ей необходимо было помочь изменить ее курс. Когда Лори рассказала о шоу своим подругам, они подумали, что это самая глупая затея из всего, что она когда-либо делала. Фотографии запечатлели такое выражение лица, словно она задавалась вопросом: «Что я творю?»
Рэй тоже хотел сбросить вес. Он недавно женился, и ему было только двадцать с лишним лет, но выглядел он на все сорок. Когда он вышел на съемочную площадку в своем купальном костюме, фотографии получились не очень привлекательные. Щелк. Улыбка. Щелк.
Сам Рэй не пошел бы на такой риск. Однако его жена хотела, чтобы он похудел, и была готова помочь ему. Она предложила соблюдать диету вместе с ним. А затем сделала еще более смелый шаг. Жена Рэя тоже надела бикини. Она не была такой же полной, как Рэй, но тоже не решилась бы носить бикини.
Жена Рея и Синди оказались в разных ситуациях. Жена Рэя не заключала сделку, как Синди. Ей не нужно было взвешиваться. Ей даже не нужно было сбрасывать вес. А ее фотографии показали бы только в случае, если бы Рэю не удалось похудеть.
Для Рэя это означало, что его ставки поднялись еще выше. Он мог потерять либо вес, либо жену.
Все эти люди, две женщины и одна супружеская пара, обнажили перед камерами свою душу, и не только. Почему они пошли на это? Они были не из тех, кто любит выставлять себя напоказ. Продюсеры АВС тщательно проверили их всех. Никто из пяти участников шоу не хотел, чтобы эти фотографии появились на ТВ; все они были уверены в том, что этого не произойдет.
Эти люди играли против своего будущего «я». Сегодняшнее «я» хочет, чтобы будущее «я» придерживалось диеты и занималось физическими упражнениями. Будущее «я» хочет мороженого и телевизора. В большинстве случаев берет верх будущее «я», потому что именно ему приходится делать что-то реальное. Весь секрет в том, чтобы изменить стимулы, движущие будущим «я», тогда изменится его поведение.
В греческой мифологии Одиссей хотел услышать пение сирен. Он знал, что, если позволит своему будущему «я» послушать эту песню, его же будущее «я» направит корабль на скалы. Поэтому он связал себе руки – в буквальном смысле слова. Одиссей приказал своим людям привязать его руки к мачте и залепить уши воском. При соблюдении диеты этот подход известен как стратегия пустого холодильника.
Синди, Лори и Рэй пошли еще дальше. Они поставили себя в такое положение, выбраться из которого им помогло бы только строгое соблюдение диеты. Возможно, вы считаете, что всегда полезно иметь больше вариантов. Но если мыслить стратегически, сокращение числа возможных вариантов событий может принести больше пользы. Томас Шеллинг пишет в своей книге о том, как афинский полководец Ксенофонт сражался, встав спиной к глубокому ущелью. Он специально выбирал такую позицию, чтобы у его солдат не было возможности отступать[21]. В той битве у них одеревенели спины, но они победили.
Точно так же Кортес потопил свои корабли после прибытия в Мексику. Это решение поддержал весь его отряд. При огромном численном преимуществе противника 600 солдат Кортеса решили, что они либо разобьют ацтеков, либо погибнут. Ацтеки могли отступить в глубь своей территории, а у солдат Кортеса не было никакой возможности для бегства или отступления. Сделав поражение еще более пагубным, чем оно было бы само по себе, Кортес повысил свои шансы на победу – и победил[22].
Что помогло Кортесу и Ксенофонту, то помогло и Синди, Лори и Рэю. Через два месяца, как раз ко Дню святого Валентина, Синди похудела почти на восемь килограммов. Рэй сбросил десять килограммов и уменьшил объем талии на две дырочки в ремне. Угроза обнародования фотографий стала тем мотивом, который заставил их начать, но когда они действительно начали работать над собой, то делали это только для себя. Лори сбросила требуемые семь килограммов за первый месяц. Но она продолжала работать и за следующий месяц похудела еще на шесть килограммов. Избавившись от тринадцати килограммов (что составило 14 процентов ее веса), Лори смогла носить одежду на два размера меньше. Ее подруги больше не считают, что участие в шоу ABC – это глупая идея.
К этому моменту вас уже не должен удивить тот факт, что один из авторов этой книги принимал участие в создании этого шоу[23]. Возможно, нам следовало бы назвать эту книгу «Стратегическое похудение» – она продавалась бы очень хорошо. Увы, мы назвали книгу иначе. Но мы еще вернемся к этому типу стратегических действий в главе 6.
В статье, посвященной реформе финансирования избирательных кампаний, «оракул из Омахи» Уоррен Баффет[24] предложил ограничить взносы частных лиц суммой от 1000 до 5000 долларов, а также запретить все остальные взносы. Никаких взносов от корпораций, профсоюзов; никаких «мягких денег». Звучит замечательно, за исключением того, что это неосуществимо.
Реформа финансирования избирательных кампаний встречает такое сопротивление, поскольку законодатели, которые должны ее одобрить, больше всего теряют, если она будет принята. Именно преимущества в сборе пожертвований гарантируют их занятость[25]. Как можно заставить людей делать то, что противоречит их интересам? Это значит поставить их в ситуацию, известную как дилемма заключенных[26]. Вот что говорит об этом Уоррен Баффет:
Представьте себе, что некий эксцентричный миллиардер (только не я!) делает такое предложение: если законопроект будет отклонен, этот эксцентричный миллиардер любым допустимым способом пожертвует миллиард долларов («мягкие деньги» делают возможным все) в пользу политической партии, которая отдаст больше всего голосов за принятие законопроекта. Благодаря такому дьявольскому применению теории игр законопроект спокойно пройдет через Конгресс, на что наш эксцентричный миллиардер не потратит ни цента (а это говорит о том, что он не так уж эксцентричен)[27].
Представьте себе, что вы законодатель от Демократической партии, и проанализируйте возможные варианты своих действий. Если вы считаете, что республиканцы поддерживают законопроект, а вы сами выступаете против, тогда в случае успеха вы обеспечите республиканцам 1 миллиард долларов, тем самым отдав в их руки ресурсы, благодаря которым они будут занимать доминирующее положение на протяжении следующих десяти лет. Следовательно, вам нет никакого смысла выступать против законопроекта, если его поддерживают республиканцы. С другой стороны, если республиканцы выступают против этого законопроекта, а вы поддерживаете его, у вас есть шанс заработать 1 миллиард долларов.
Таким образом, что бы ни делали республиканцы, демократы должны поддержать законопроект. Разумеется, та же логика применима и к республиканцам. Они должны поддержать законопроект независимо от позиции демократов. В итоге обе партии поддержат законопроект, а наш миллиардер получит желаемое даром. Баффет отмечает, что сам факт эффективности такого плана «подтвердил бы абсурдность заявлений о том, что деньги не влияют на голоса конгрессменов».
Такая ситуация обозначается термином «дилемма заключенных», поскольку обе стороны вынуждены предпринимать действия, противоречащие их взаимным интересам[28]. В классическом варианте дилеммы заключенных полиция допрашивает двух подозреваемых отдельно друг от друга. Каждому из них предлагают сознаться и обещают гораздо более суровый приговор, если он не успеет сознаться первым. Таким образом, каждый из заключенных считает для себя более выгодным признаться в совершении преступления, хотя обоим было бы лучше, если бы они молчали.
Трумен Капоте приводит наглядный пример дилеммы заключенных в своей книге «Хладнокровное убийство»[29]. Ричард «Дик» Хикок и Перри Эдвард Смит арестованы за бессмысленное убийство семьи Клаттеров. Свидетелей не было, однако тюремный осведомитель назвал полиции их имена. Во время допроса полиция настроила их друг против друга. Капоте позволяет нам проникнуть в мысли Перри:
…Это, как и выдуманный «свидетель», было сказано просто для того, чтобы заставить его подергаться. Этого не может быть. Или они имеют в виду… Эх, если бы он только мог поговорить с Диком! Но их держали порознь; Дик сидел в камере на другом этаже. …А Дик? Возможно, они и с ним провернули такой же трюк. Дик был умным, убедительным актером, но «стержня» в нем нет, он слишком легко поддается панике. …«И прежде чем уйти из этого дома, вы убили всех, кто там был». Очень может быть, что каждому из бывших заключенных в Канзасе они поют одну и ту же песенку. Они, наверное, допросили сотни людей и многих из них обвинили в этом убийстве; мы с Диком просто еще двое таких же…
И Дик тоже не спал в своей камере ниже этажом и, как он вспоминал позже, так же жаждал поговорить с Перри – выяснить, что этот урод им рассказал[30].
В итоге признался сначала Дик, а затем и Перри[31]. Такова природа этой игры.
Проблема коллективных действий – один из вариантов дилеммы заключенных, хотя в таком случае «заключенных» не двое, а гораздо больше. В одной детской сказке мыши решили, что жить им было бы гораздо безопаснее, если бы у кота на шее висел колокольчик. Проблема в одном: кто рискнет жизнью, чтобы повесить колокольчик коту на шею?
С такой проблемой сталкиваются и мыши, и люди. Как диктаторам, не пользующимся любовью народа, удается долго управлять огромными массами людей? Почему один хулиган может терроризировать всю школу? В обоих случаях слаженные действия масс имеют хорошие шансы на успех.
Однако процесс коммуникации и координации, необходимый для совершения таких действий, сопряжен с большими трудностями, а диктаторы, зная силу масс, предпринимают особые меры, чтобы еще более затруднить этот процесс. Когда люди вынуждены действовать порознь и только надеются на то, что когда-нибудь наступит подходящий момент, возникает вопрос: «Кто будет первым?» Такой лидер заплатит большую цену – разбитый нос или даже жизнь. А наградой ему будет посмертная слава или благодарность потомков. В этом мире есть люди, которыми движет долг или честь, но большинство считает, что такая цена превосходит возможные выгоды.
Хрущев впервые выступил с осуждением сталинских чисток на ХХ съезде Коммунистической партии Советского Союза. После его драматической речи кто-то из присутствующих спросил, чем в это время занимался он сам. Хрущев попросил задавшего этот вопрос встать и назвать свое имя. Зал молчал. Хрущев произнес: «Вот этим занимался и я».
Каждый человек действует в собственных интересах, что приводит к неблагоприятным последствиям для всей группы. По всей видимости, дилемма заключенных – самая сложная в теории игр. Мы вернемся к этой теме в главе 3, чтобы обсудить, что можно предпринять в данном случае. Но должны с самого начала предупредить вас: мы не утверждаем, что исход игры устроит игроков. Многие экономисты (в том числе и мы сами) без устали твердят о преимуществах свободного рынка. Этот вывод основан на предположении о том, что система свободного ценообразования определяет поведение индивида. В большинстве случаев стратегического взаимодействия нет невидимой руки рынка, которая руководила бы действиями пекаря, мясника или любого другого человека. Следовательно, нет и оснований ожидать, что исход игры будет благоприятным для отдельных ее участников или для общества в целом. Недостаточно играть хорошо – вы должны быть уверены в том, что играете в правильную игру.
Судя по всему, у Такаши Хашиямы[32] проблемы с принятием решений. Два крупнейших аукционных дома, Sotheby’s и Christie’s, сделали весьма привлекательные предложения о проведении аукциона по продаже коллекции произведений искусства стоимостью в 18 миллионов долларов, принадлежащей его компании. Вместо того чтобы выбрать один аукционный дом из этих двух, Хашияма предложил обоим сыграть в игру «камень, ножницы, бумага» и так определить победителя. Да, да, «камень, ножницы, бумага». Камень разбивает ножницы, ножницы разрезают бумагу, а бумага обертывает камень.
В Christie’s выбрали ножницы, в Sotheby’s – бумагу. Ножницы режут бумагу, поэтому аукционный дом Christie’s получил заказ и заработал комиссионные в 3 миллиона долларов. Учитывая, что ставки были столь высокими, могла ли теория игр помочь в этой ситуации?
На первый взгляд может показаться, что в такой игре невозможно предсказать действия ее участников. Если бы в Sotheby’s знали, что в Christie’s выберут ножницы, тогда там выбрали бы камень. Не имеет значения, что вы выберете: всегда найдется то, что окажется сильнее. Следовательно, очень важно, чтобы соперник не мог предсказать ваш ход.
В процессе подготовки к игре представители Christie’s обратились за советом к местным экспертам, а именно – к детям своих служащих, которые регулярно играют в эту игру. Одиннадцатилетняя Элис сказала следующее: «Все знают, что всегда нужно начинать с ножниц». Флора, сестра-близняшка Элис, добавила свое мнение: «Камень – это слишком очевидно, а ножницы бьют бумагу. Поскольку они новички, им лучше всего начать с ножниц»[33].
В Sotheby’s придерживались другого подхода. Там считали, что это дело случая, поэтому здесь нет места для стратегии. Выбор бумаги был не хуже остальных вариантов.
В этом примере интересно то, что каждая сторона по-своему права. Если бы в Sotheby’s выбрали свою стратегию произвольно (исходя из того, что камень, ножницы и бумага имеют равные шансы), то что бы ни предпочли в Christie’s, было бы в равной степени хорошо. Каждый вариант имеет одну треть шансов на выигрыш, одну треть – на проигрыш, и одну треть – на ничью.
Но в Christie’s выбрали стратегию не случайным образом. Следовательно, представителям Sotheby’s стоило бы подумать о том, какой совет могут получить в Christie’s, и сделать все возможное, чтобы переиграть их. Если всем действительно известно, что начинать следует с ножниц, тогда Sotheby’s лучше начать с любимого выбора Барта Симпсона[34] – старого доброго камня.
В каком-то смысле оба участника этой игры наполовину неправы. Поскольку у Sotheby’s не было стратегии, усилия Christie’s не имели смысла. Но именно с учетом этих усилий Christie’s представителям Sotheby’s стоило бы рассуждать стратегически.
Когда речь идет об одном сеансе игры, делать произвольный выбор не так уж сложно. Но если игра повторяется, необходимо найти более искусный подход. Смешивание ходов не сводится к предсказуемой смене стратегий. Ваш соперник, понаблюдав за вами, может столь же легко использовать любую закономерность в вашей игре, как и многократное повторение одной неизменной стратегии. Непредсказуемость – вот что самое важное в смешивании ходов.
Как оказалось, большинство людей ведут себя предсказуемо. Вы можете проверить это сами, сыграв в игру «камень, ножницы, бумага» в режиме онлайн: компьютерные программы способны распознавать закономерности, поэтому и побеждают вас[35]. Пытаясь все запутать, игроки слишком часто применяют одни и те же стратегии поочередно. Это приводит к неожиданному успеху «лавинной» стратегии: камень, камень, камень.
Кроме того, людям свойственно принимать решения под влиянием того, что сделала другая сторона в прошлый раз. Если бы и Sotheby’s, и Christie’s начали игру с ножниц, была бы ничья и игру пришлось бы начинать заново. Учитывая то, что сказала Флора, в Sotheby’s рассчитывали бы, что Christie’s сыграет камнем (чтобы побить их ножницы). Поэтому в Sotheby’s выбрали бы бумагу, а в Christie’s отдали бы предпочтение ножницам. Разумеется, такой шаблонный подход тоже не может быть правильным. Если бы он был верным, в Sotheby’s могли бы сыграть камнем и одержать победу.
Представьте себе, что произошло бы, если бы существовала некая известная всем формула выбора объектов для проведения налоговой проверки. Перед подачей налоговой декларации вы могли бы с помощью этой формулы определить, будет ли налоговая служба вас проверять. Если проверка возможна, но вы видите способ «подкорректировать» свою декларацию о доходах до тех пор, пока формула больше не будет предсказывать проверку, скорее всего, вы так бы и сделали. Если же проверка неизбежна, вы предпочли бы сказать правду. Предсказуемость действий налоговой службы закончилась бы тем, что налоговая проверка проводилась бы не там, где следовало. Все, кто попадает под проверку, знали бы, что их ждет, и предпочли бы действовать честно. С другой стороны, те люди, которым удалось избежать проверки, отвечали бы только перед своей совестью. Если налоговая служба выбирает объекты для проверки в произвольном порядке, попасть под такую проверку рискуют все, и это создает дополнительный стимул для честности.
Важность рандомизированной стратегии оказалась одним из первых открытий теории игр. Это достаточно простая и интуитивно понятная идея, но она требует уточнения, чтобы ее можно было успешно использовать на практике. Теннисисту недостаточно знать, что ему придется отбивать подачи соперника слева и справа. Он должен иметь какое-то представление о том, как часто ему придется отбивать удар справа – в 30 или 64 процентах случаев; ему также необходимо понимать, что ответ на этот вопрос зависит от относительной силы ударов с обеих сторон. В главе 5 мы расскажем о методах, позволяющих найти ответ на этот вопрос.
Мы хотели бы завершить этот раздел следующим замечанием. В игре «камень, ножницы, бумага» больше всех проиграл не аукционный дом Sotheby’s, а господин Хашияма. Его решение использовать эту игру предоставило двум аукционным домам равные возможности заработать комиссионные. Вместо того чтобы позволять двум соперникам договориться о разделе комиссионных, он мог бы устроить свой собственный аукцион. Обе компании были готовы и даже весьма заинтересованы в том, чтобы взять на себя продажу его коллекции произведений искусства и получить при этом 12 процентов комиссионных[36]. Победителем стал бы тот аукционный дом, который предложил более низкую ставку. Я слышу 11 процентов? Раз… два…
В фильме Guys and Dolls[37] азартный игрок Скай Мастерсон рассказывает о том, какой ценный совет он получил когда-то от своего отца:
Однажды ты встретишь на своем пути парня, который покажет тебе абсолютно новую, нераспечатанную колоду карт. Затем он предложит тебе пари на то, что вытянет из колоды пикового валета, и если выиграет, то пустит тебе струю сидра в ухо. Но, сынок, ни в коем случае не соглашайся на это пари, иначе ты закончишь тем, что в твоем ухе будет полно сидра – и это так же верно, как то, что ты стоишь здесь передо мной.
В одном из эпизодов фильма Натан Детройт предложил Скаю Мастерсону такое пари: чего Минди продает больше – штруделей или творожных пирогов. Натан знал правильный ответ (штрудели) и был готов поручиться, что Скай поставит на творожный пирог[38].
На первый взгляд этот пример может показаться крайностью. Разумеется, никто не стал бы заключать столь глупое пари. Или стал бы? Посмотрите на рынок фьючерсных контрактов на Чикагской бирже опционов. Когда какой-то биржевой игрок предлагает продать вам фьючерсный контракт, он заработает деньги только в случае, если вы их потеряете[39].
Если вы фермер и выращиваете сою на продажу, тогда фьючерсный контракт станет вашей страховкой от риска неблагоприятного колебания цен в будущем. Точно так же, если вы продаете соевое молоко и вам необходимо будет купить сою, для вас такой контракт – тоже страховка, а не азартная игра.
Однако объем торгов фьючерсными контрактами на бирже говорит о том, что большинство людей, которые покупают и продают их, – это трейдеры, а не фермеры или производители. Для них эта сделка представляет собой игру с нулевой суммой. Когда оба участника сделки соглашаются заключить ее, каждый из них считает, что заработает деньги. Следовательно, один из участников сделки ошибается. Таков характер игры с нулевой суммой: выигрывает только одна сторона.
В этом и есть парадокс. Как могут оба участника сделки считать, что они перехитрят друг друга? Кто-то из них наверняка неправ. Почему вы считаете, что ошибается кто-то другой, а не вы? Предположим, у вас нет инсайдерской информации. Если кто-то готов продать вам фьючерсный контракт, любые деньги, которые вы заработаете, потеряет другая сторона. Почему вы считаете, что вы умнее? Не забывайте: другой участник сделки готов заключить ее с вами только потому, что считает себя умнее вас.
В покере игроки сталкиваются с этим парадоксом, когда дело доходит до повышения ставок. Если игрок делает ставки только тогда, когда у него хорошие карты, другие участники игры вскоре поймут это. В ответ на повышение ставок они откажутся от борьбы, так что этот игрок не сможет сорвать большой банк. Если найдутся игроки, которые пойдут на повышение ставок, это означает, что у них карты еще лучше, поэтому нашего бедного игрока ожидает большой проигрыш. Другие игроки могут сыграть против сильной карты, только если им кажется, что вы блефуете. Для того чтобы убедить их в этом, следует делать ставки достаточно часто, время от времени допуская при этом блеф. В результате возникает интересная дилемма. Вы хотели бы, чтобы другие игроки сбросили карты, когда вы блефуете, это дало бы вам возможность выиграть с плохими картами. Но тогда вы не сможете победить, взяв большой банк. Чтобы убедить других игроков в необходимости поднять ставки, вам нужно, чтобы вас поймали на блефе.
Чем опытнее игроки, тем труднее убедить их в том, чтобы они делали против вас большие ставки. Возьмем в качестве примера эпизод игры с крупными ставками между Эриком Линдгреном и Дэниелом Негреану – двумя ведущими игроками в покер.
…Негреану, почувствовав плохую карту, поднял ставки на две тысячи долларов. «Я уже поставил двести семьдесят тысяч, так что у меня осталось две тысячи», – сказал Негреану. Но Эрик смотрит на мои фишки и говорит: «Сколько у тебя осталось?» – и идет ва-банк, поставив на кон все, что у него было. Согласно правилам турнира, у Негреану было всего 90 секунд на принятие решения о том, стоит ли ему делать такую же ставку. При этом он рисковал проиграть все свои деньги, если Линдгрен блефует, или ему пришлось бы сбросить карты и потерять изрядную сумму тех денег, которые он уже внес в банк.
«Я не думал, что он может быть настолько глупым, – сказал Негреану. – Но он и не был глупым. Он просто был на шаг впереди. Он знал, что я знаю, что он не сделает такую глупость, поэтому, сделав эту так называемую глупость, он на самом деле прекрасно сыграл»[40].
Разумеется, не следует делать ставки против таких чемпионов покера – но когда же все-таки стоит рискнуть? Граучо Маркс[41] однажды произнес ставшую знаменитой фразу о том, что он ни за что не вступил бы в клуб, который согласится его принять. По той же причине, возможно, не стоит принимать пари, которые предлагают вам другие люди. У вас должно вызвать обеспокоенность даже то, что вы выиграли аукцион: тот факт, что вы предложили самую большую сумму, означает, что другие участники аукциона не считают предмет торгов таким ценным, как вы. Существует особый термин для обозначения ситуации, когда кто-то выигрывает аукцион, а затем обнаруживает, что переплатил: «проклятие победителя».
Каждое действие говорит нам кое-что о том, что известно человеку, который его совершил, и вы должны использовать эту информацию наряду с тем, что знаете сами, в качестве руководства к действию. В главе 10 мы расскажем о том, как избежать «проклятия победителя», принимая участие в аукционах.
Существуют правила игры, которые поставят вас в равные условия с другими игроками. Один из способов заключения сделок при наличии односторонней информации заключается в том, чтобы предложить менее информированному участнику сделки выбрать, какую позицию занять. Если бы Натан Детройт заранее согласился заключить пари, какую бы сторону ни выбрал Скай, ему не помогла бы даже имеющаяся у него информация. На фондовом и валютном рынке, а также на других финансовых рынках люди могут занимать любую сторону сделки. На некоторых биржах, в том числе на Лондонской фондовой, когда вы спрашиваете о котировке акций, маркетмейкер обязан назвать вам и цену покупки, и цену продажи еще до того, как он узнает, на какой стороне сделки вы находитесь. Без таких превентивных мер маркетмейкеры могли бы получать прибыль за счет конфиденциальной информации, а сторонние инвесторы так боялись бы обмана, что это могло бы привести к обвалу всего рынка. Цена покупки и цена продажи не равны друг другу; разница между ними обозначается термином «спред между ценой продавца и покупателя». На ликвидных рынках такой спред совсем небольшой, а это говорит о том, что любой приказ на покупку или на продажу содержит не так уж много информации. Мы вернемся к роли информации в главе 8.
Однажды поздно вечером после конференции в Иерусалиме два американских экономиста (в том числе один из авторов этой книги) взяли такси и попросили водителя отвезти их в отель. Водитель сразу же понял, что они американские туристы, и отказался включать счетчик. Вместо этого он заявил, что любит американцев, и пообещал взять с нас меньше денег, чем было бы по счетчику. Разумеется, мы несколько скептически отнеслись к его обещанию. С какой стати этот незнакомец станет предлагать нам более низкую цену, чем по счетчику, если мы готовы заплатить то, что с нас причитается? Как мы вообще узнаем, не слишком ли большую цену назначил водитель?
С другой стороны, мы не обещали водителю заплатить больше, чем по счетчику. Мы решили воспользоваться своими знаниями теории игр. Если мы сразу же начнем торговаться, а наши переговоры зайдут в тупик, нам придется искать другое такси. Но если мы отложим эти переговоры до того момента, когда приедем в отель, наша позиция будет гораздо сильнее. А найти такси было очень трудно.
И вот мы приехали. Водитель потребовал 2500 израильских шекелей (2,75 доллара). Кто знает, была ли эта сумма справедливой? Поскольку в Израиле принято торговаться, Барри возразил против такой суммы и предложил 2200 шекелей. Водитель пришел в ярость. Он заявил, что невозможно добраться оттуда сюда за такую сумму. Прежде чем мы смогли продолжить переговоры, он заблокировал все двери и с головокружительной скоростью отправился по обратному маршруту, игнорируя сигналы светофора и пешеходов. Неужели нас похитили и везут в Бейрут? Нет. Наш водитель вернулся на то место, где мы сели в его такси, довольно грубо прогнал нас из салона и прокричал вслед: «Посмотрим, как далеко вы теперь уедете за 2200 шекелей».
Мы нашли другое такси и ровно за 2200 шекеля добрались до отеля.
Разумеется, потраченное нами время не стоило трехсот шекелей. С другой стороны, сама эта история стоила денег. Она показывает, насколько опасно вести переговоры с тем, кто еще не читал нашу книгу. Короче говоря, гордость и иррациональность игнорировать нельзя. Иногда лучше дать обвести себя вокруг пальца, если это обойдется вам совсем недорого.
Из этой истории можно извлечь еще один урок. На самом деле мы поступили в той ситуации не очень дальновидно. Представьте себе, насколько сильнее была бы наша позиция в переговорах с водителем, если бы мы начали обсуждать цену уже после того, как вышли из автомобиля. (Разумеется, когда вы нанимаете такси, необходимо придерживаться обратной логики. Если вы скажете водителю, куда вам нужно ехать, еще до того, как сесть в машину, это может закончиться тем, что ваш таксист сразу начнет искать другого клиента. Сначала сядьте в такси, а затем говорите, куда вам нужно ехать.)
Через несколько лет после публикации этой истории мы получили следующее письмо:
Дорогие профессора!
Вы, конечно же, не знаете моего имени, но, думаю, вспомните мою историю. Я учился в Иерусалиме, а по вечерам подрабатывал водителем такси. Теперь я работаю консультантом. Я случайно наткнулся на вашу книгу, когда она была опубликована на иврите. Возможно, вам будет интересно, что я тоже рассказываю эту историю своим клиентам. Да, все это действительно происходило поздно вечером в Иерусалиме. Что же касается остального, насколько я помню, все было несколько иначе.
Из-за учебы и работы по вечерам у меня почти не оставалось времени, которое я мог бы проводить со своей невестой. Поэтому я нашел такой выход: решил брать ее с собой в поездки по городу, посадив на переднее сиденье. Хотя она и молчала тогда, с вашей стороны было большой ошибкой не упомянуть о ней в своем рассказе.
Мой счетчик сломался, но вы мне не поверили. А я слишком устал, чтобы спорить. Когда мы приехали, я запросил с вас вполне справедливую цену – 2500 шекелей. Я даже надеялся, что вы округлите эту сумму до 3000 шекелей. Вы, богатые американцы, вполне могли себе позволить заплатить 50 центов чаевых.
Я поверить не мог, что вы пытаетесь обвести меня вокруг пальца. Ваш отказ заплатить справедливую цену опозорил меня в глазах моей невесты. Хотя я и был беден, я не нуждался в ваших подачках.
Вы, американцы, считаете, что мы должны радоваться каждой крошке, которую вы нам бросаете. Но послушайте: мы должны преподать вам урок игры под названием жизнь. Мы с женой вместе уже двадцать лет, и мы до сих пор смеемся над глупыми американцами, которые потратили полчаса на поездки в такси туда-сюда, лишь бы сэкономить каких-то двадцать центов.
Искренне ваш,
(имя не указано)
По правде говоря, мы не получали такого письма. Мы просто хотели проиллюстрировать один важный урок теории игр: необходимо понимать позицию другого игрока. Вы должны проанализировать, что он знает, что его мотивирует и даже что он думает о вас. В известном высказывании Джорджа Бернарда Шоу о золотом правиле идет речь о том, что не следует поступать с другими так, как вы хотели бы, чтобы они поступали с вами, ведь у них могут быть совсем другие вкусы. Стратегическое мышление подразумевает, что вы должны приложить максимум усилий к тому, чтобы понять позицию и взаимосвязи между другими участниками игры, в том числе позицию тех игроков, которые предпочитают молчать.
Мы подошли к последнему важному моменту. Вам может казаться, что вы играете в одну игру, тогда как это всего лишь часть более крупной игры. Более крупная игра есть всегда.
Приведенные примеры познакомили нас с принципами принятия стратегических решений. Далее представим краткую формулировку этих принципов в виде уроков, извлеченных из наших историй.
Мыслите по принципу 4:8, когда пытаетесь разобраться, к чему стремится другой игрок[42]. Вспомните о способности Ричарда Хэтча просчитать все дальнейшие шаги, чтобы понять, что следует делать. История о «счастливой руке» учит, что в стратегии, как и в физике, «на всякое действие есть противодействие». Мы живем и действуем не в вакууме. Следовательно, не можем рассчитывать на то, что, когда мы изменим свое поведение, все остальное останется неизменным. Успех Шарля де Голля в переговорах означает, что «заклинившее колесо получает смазку»[43]. Однако проявлять непреклонность не так уж и легко, особенно если приходится быть еще более непреклонным, чем упрямый соперник. Этим упрямым соперником вполне может оказаться ваше будущее «я», тем более если речь идет о соблюдении диеты. Если вы сражаетесь или следуете диете, отрезав пути к отступлению, это поможет вам укрепить свою решимость.
Истории о дилемме заключенных и о мышах, которые мечтали о том, чтобы на шее кота висел колокольчик, показывают, как трудно добиться результата, если это требует координации действий и самопожертвования. В технологических гонках в не меньшей степени, чем в парусных, отстающие пытаются использовать более инновационные стратегии, а лидеры часто имитируют действия тех, кто следует за ними.
Пример с игрой «камень, ножницы, бумага» подчеркивает стратегическое преимущество непредсказуемости ваших действий. Такой образ действий имеет и дополнительный плюс: он делает жизнь немного более интересной. Наш водитель такси дает понять, что другие участники игры – тоже люди, а не машины. Гордость, раздражение и другие эмоции могут воздействовать на их решения. Поставить себя на место другого человека – это значит воспринимать ситуацию с его, а не с вашей точки зрения.
Мы могли бы привести еще много других примеров и извлечь из них определенные уроки, но это не самый удачный способ методического изучения стратегических игр. Для этого лучше подойти к данной теме по-иному. Мы выбираем определенный принцип (например, стратегическое обязательство, сотрудничество или смешивание стратегий) и анализируем иллюстрирующие этот принцип примеры до тех пор, пока вы не поймете его суть в полной мере. Затем предоставим вам возможность применить данный принцип в учебном примере, который приводится в конце соответствующей главы.
Мы считаем, что все происходящее в жизни – это игра, даже то, что на первый взгляд игрой не кажется. Возьмем в качестве примера следующий вопрос из GMAT (Graduate Management Admissions Test) – теста для поступающих в магистратуру по курсу менеджмента.
К сожалению, авторские права не позволяют привести здесь сам вопрос, но это не должно нас останавливать. Какой из следующих вариантов ответа правильный:
а) 4π кв. дюймов
b) 8π кв. дюймов
c) 16 кв. дюймов
d) 16π кв. дюймов
e) 32π кв. дюймов
Мы понимаем, что вы находитесь в невыгодном положении, поскольку не знаете самого вопроса. И все же считаем, что, применив теорию игр, сможете найти правильный ответ.
Анализ примера
В этой серии ответов из общей закономерности выпадает ответ c. Поскольку он так отличается от остальных ответов, есть вероятность, что это неправильный ответ. Учитывая, что во всех ответах в качестве единицы измерения указан квадратный дюйм, можно предположить, что в ответе должен быть полный квадрат, например 4π или 16π.
Это хорошее начало, которое говорит о наличии неплохих навыков сдачи тестов, но мы еще даже не начали применять теорию игр. Подумайте о том, какую игру ведет человек, составляющий эти вопросы. Каковы его цели?
Этому человеку нужно, чтобы люди, которые понимают задачу, нашли правильный ответ, а люди, не понимающие задачу, не смогли бы ее решить. Следовательно, необходимо тщательно подобрать неправильные ответы с точки зрения их привлекательности для тех, кто не знает правильного ответа. Например, если на вопрос «Сколько футов в одной миле?» среди возможных вариантов есть ответы «жираф» или даже «16π», вряд ли их выберет кто-либо из сдающих тест.
Теперь проанализируем ситуацию с другой стороны. Предположим, 16 квадратных дюймов – это и есть правильный ответ. Какой вопрос нужно поставить, чтобы правильный ответ был 16 квадратных дюймов, но человек, сдающий тест, подумал бы, что верный ответ – 32π квадратных дюйма? Таких вопросов не так уж много. Людям не свойственно использовать число π просто ради забавы. «Ты видел мою новую машину? Она проезжает 10π миль на одном галлоне бензина». Следовательно, мы можем смело исключить 16 квадратных дюймов из числа правильных ответов.
Теперь проанализируем полные квадраты: 4π и 16π. Предположим, правильный ответ – 16π квадратных дюймов. Возможно, вопрос был поставлен так: чему равна площадь круга с радиусом 4 дюйма? Формула вычисления площади круга выглядит так: πr2. Однако тот, кто не помнит формулу площади круга, мог бы перепутать ее с формулой длины окружности, 2πr. (Да, мы знаем, что длина окружности измеряется в дюймах, а не в квадратных дюймах, но человек, способный допустить такую ошибку, вряд ли понимает это.)
Обратите внимание, что если r = 4, тогда 2πr равно 8π – из-за этого человек может выбрать неправильный ответ b. Кроме того, этот человек может еще больше все перепутать и использовать формулу 2πr2, что заставит его выбрать 32π, или ответ e, в качестве правильного. Этот человек может опустить π и выбрать ответ 16, или с, либо забыть о том, что нужно возвести радиус в квадрат, и выберет формулу πr для вычисления площади, что наведет его на мысль выбрать ответ 4π, или а. В общем, если правильный ответ – 16π, мы можем привести убедительные доводы в пользу того, как человек, сдающий тест, может выбрать каждый из оставшихся неправильных ответов.
Но что если правильный ответ – 4π (тогда r = 2)? Вспомните о том, что люди часто допускают ошибку, путая окружность с площадью. Если студент использует неправильную формулу 2πr, он получит 4π, хотя и с неправильной единицей измерения. С точки зрения человека, составляющего тест, нет ничего хуже, чем позволить сдающему тест получить правильный ответ на основании ошибочных рассуждений. Следовательно, ответ 4π был бы худшим правильным ответом, поскольку позволил бы слишком многим некомпетентным людям выбрать правильный ответ и сдать тест.
На этом этапе можно прекратить дальнейший анализ. Мы убеждены в том, что правильный ответ – 16π. Поразмышляв о целях составителя теста, мы можем вычислить правильный ответ, даже не зная самого вопроса.
Тем не менее мы не рекомендуем вам сдавать тесты, не ознакомившись сначала с вопросами. Мы допускаем, что если вы достаточно умны, чтобы понять всю эту логику, значит, наверняка знаете формулу площади круга. Но в жизни бывает всякое. Вы вполне можете столкнуться с ситуацией, когда среди ответов на тестовые вопросы встретится нечто совершенно вам незнакомое или соответствующий материал не был охвачен в том курсе, который вы изучали. В таких случаях анализ игры под названием «сдача тестов» поможет вам найти правильный ответ.
Глава 2. Решение игр методом обратных рассуждений
В комиксе Peanuts («Крошки») повторяется такой эпизод: Люси держит мяч на земле и предлагает Чарли Брауну разбежаться и ударить по нему. В самый последний момент Люси убирает мяч, Чарли Браун, взмахнув ногой по воздуху, падает на спину, а Люси злорадствует.
Любой посоветовал бы Чарли отказаться играть с Люси. Даже если бы Люси не проделала эту выходку с ним в прошлом году (и год назад, и еще годом раньше), Чарли уже знаком с ее характером, так что мог бы предсказать ее действия.
Когда Чарли решает, стоит ли ему принимать предложение Люси, ее действия относятся к будущему. Но тот факт, что она совершит эти действия в будущем, не означает, что Чарли должен считать их непредсказуемыми. Ему следовало бы знать, что из двух вариантов (позволить ему ударить по мячу и посмотреть, как он падает) Люси, скорее всего, отдаст предпочтение последнему. Следовательно, Чарли должен исходить из того, что, когда придет время, она отодвинет мяч в сторону. Если рассуждать логически, вероятность того, что Люси позволит Чарли ударить по мячу, на самом деле крайне мала. Полагаться на такую вероятность – значит допустить победу надежды над опытом, как сказал доктор Джонсон[44] по поводу повторного брака. Чарли должен отбросить эту вероятность как несущественную и предвидеть, что, приняв предложение Люси, он неизбежно упадет на спину. Это значит, что ему следует отклонить предложение.










Отличительный признак любой стратегической игры – взаимозависимость решений игроков. Участники такой игры могут придерживаться двух способов взаимодействия. Первый способ – это последовательное взаимодействие, как в случае с Чарли Брауном. Когда наступит очередь Чарли принимать решение, он должен заглянуть в будущее и проанализировать, как его текущие действия повлияют на действия Люси, а также на его собственные действия в будущем.
Второй способ – это параллельное взаимодействие, как в истории о дилемме заключенных, изложенной в главе 1. В этом случае игроки действуют одновременно, ничего не зная о текущих действиях других игроков. Тем не менее каждый участник игры должен осознавать, что есть и другие активные игроки, которые тоже понимают, что они не одни в этой игре, и так далее. Следовательно, каждому участнику игры нужно поставить себя на место всех остальных игроков и попытаться вычислить результат игры. Его собственный оптимальный ход – неотъемлемый элемент таких расчетов.
Играя в стратегическую игру, вы должны определить, какой тип взаимодействия в ней присутствует – параллельный или последовательный. В некоторых играх, таких как футбол, есть элементы взаимодействия обоих типов. Это означает, что вы должны привести свою стратегию в соответствие с конкретной ситуацией. В этой главе дано общее описание тех идей и принципов, которые помогут вам играть в последовательные игры; игры с параллельными ходами – это тема главы 3. Мы начинаем с достаточно простых примеров, вроде истории с Чарли Брауном. Это сделано с определенной целью: такие истории сами по себе не представляют большой ценности, а правильные стратегии можно легко найти посредством обычной интуиции, что позволяет четко обозначить основные идеи. В следующих главах приводятся более реалистичные и сложные учебные примеры.
Общий принцип всех игр с последовательными ходами гласит, что каждый игрок должен проанализировать будущие ответные действия других игроков и эту информацию использовать для поиска своего оптимального хода в настоящем. Эта идея настолько важна, что ее необходимо сформулировать в виде основного правила стратегического поведения:
ПРАВИЛО № 1: смотрите вперед и рассуждайте в обратном порядке.
Проанализируйте, к чему могут привести ваши первоначальные решения, и на основе этой информации рассчитайте оптимальный ход.
В истории с Чарли Брауном сделать это было достаточно легко любому желающему (кроме самого Чарли Брауна). Из двух возможных вариантов он выбрал тот, на котором – также из двух возможных – остановилась и Люси. Большинство стратегических ситуаций содержат более длинную последовательность решений с несколькими вариантами выбора в каждой точке принятия решения. Процесс принятия правильных решений в таких играх можно представить в виде древовидной схемы. Позвольте объяснить вам, как пользоваться такими «деревьями».
В контексте первого правила стратегической игры (смотреть вперед и рассуждать в обратном порядке) последовательность решений возможна даже тогда, когда решения принимает один человек, не вовлеченный в стратегическую игру с другими людьми. Возьмем в качестве примера фрагмент стихотворения Роберта Фроста о дороге в осеннем лесу[45]:
И если станет жить невмоготу,
Я вспомню давний выбор поневоле:
Развилка двух дорог – я выбрал ту,
Где путников обходишь за версту.
Всё остальное не играет роли[46].
Представим эту ситуацию в виде следующей схемы:
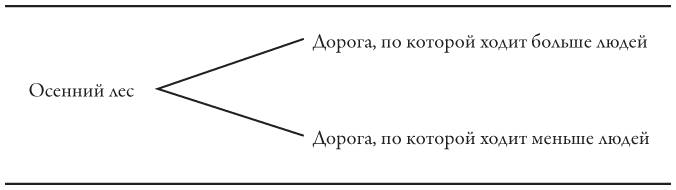
Но на этом выбор не должен заканчиваться. У каждой дороги могут быть свои развилки, а значит, карта дорог будет более сложной. Вот пример из нашей собственной жизни.
У путешественников, которые хотят добраться из Принстона в Нью-Йорк, есть выбор. В первой точке принятия решения им необходимо определить способ передвижения: автобусом, поездом или автомобилем. Те, кто предпочитает машину, могут выбрать мост Верразано-Нэрроуз, тоннель Холланда, тоннель Линкольна или мост Джорджа Вашингтона. Те, кто сядет на поезд, должны решить, стоит ли им пересесть на поезд PATH[47] или ехать дальше, до Пенсильванского вокзала. Оказавшись в Нью-Йорке, путешественникам, которые выбрали поезд или автобус, предстоит подумать, как им добираться до пункта назначения дальше: пойти пешком, поехать на метро (воспользовавшись обычной местной или скоростной линией), автобусом или на такси. Оптимальный выбор зависит от многих факторов, таких как цена, скорость, возможные транспортные пробки, конечный пункт в Нью-Йорке или даже просто нежелание дышать воздухом платной автострады в Нью-Джерси.
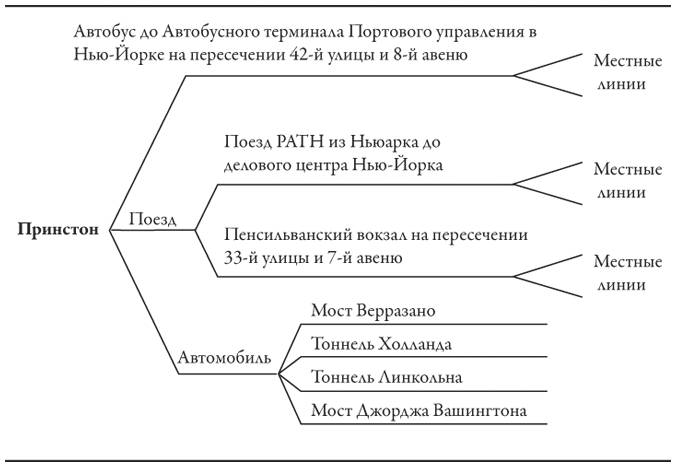
Дорожная карта, на которой представлены возможные варианты в каждой точке разветвления дальнейшего пути, напоминает дерево с ветвями, появляющимися одна за другой, поэтому такую схему и называют деревом. Правильный способ использования такой карты, или дерева, состоит не в том, чтобы выбирать маршрут, первая ветвь которого покажется вам самой лучшей – например, потому, что вы предпочитаете ездить на машине, а не поездом при прочих равных условиях, а затем поедете по мосту Верразано-Нэрроуз, когда до него доберетесь. Вы должны проанализировать свои будущие действия и использовать полученную информацию для того, чтобы сделать правильный выбор на более ранних этапах. Например, если вы хотите попасть в деловой район города, лучше поехать скоростным поездом, а не автомобилем, поскольку скоростная подземная дорога PATH обеспечивает прямое сообщение между Ньюарком и деловым центром Нью-Йорка.
С помощью такого дерева можно показать возможные варианты развития событий в стратегической игре, но в этом случае прибавится еще один элемент. В любой игре участвуют не менее двух человек. Следовательно, в разных точках ветвления дерева решения могут принимать разные игроки. Человеку, который делает выбор в той или иной точке ветвления, необходимо проанализировать не только свои будущие решения, но и решения других игроков. Он должен предвидеть, что они сделают, попытаться поставить себя на их место и поразмышлять так, как размышляли бы в соответствующей ситуации они. Для того чтобы подчеркнуть разницу, мы будем использовать два термина для обозначения деревьев: «дерево игры» – это дерево, которое отображает последовательность решений в стратегической игре; «дерево решений» представляет последовательность решений, принимаемых одним человеком.
История о Чарли Брауне, которая открыла эту главу, чрезвычайно проста, но она поможет ознакомиться с концепцией дерева игры. Игра начинается в тот момент, когда Люси предлагает Чарли ударить по мячу, а Чарли должен решить, стоит ли ему принимать это предложение. Если Чарли откажется, игра на этом закончится. Если он примет предложение Люси, она должна будет выбрать: позволить Чарли ударить по мячу или убрать мяч в сторону. Мы можем показать это, прибавив еще одну развилку на этой «дорожной карте».
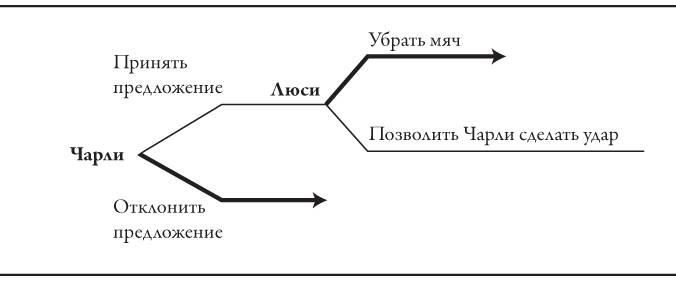
Как уже сказано, Чарли должен быть готов к тому, что Люси выберет верхнюю ветвь. Следовательно, ему нужно удалить нижнюю ветвь из вариантов выбора Люси. Если он сам выберет верхнюю ветвь, это непременно приведет к неприятному падению. Таким образом, для Чарли лучший выход – выбрать нижнюю ветвь. На рисунке эти варианты выбора обозначены жирными линиями со стрелками.
Вы считаете, что это слишком простой пример? Вот его вариант в сфере бизнеса. Представьте себе следующий сценарий. Уже будучи взрослым, Чарли проводит отпуск в бывшей марксистской стране Фридонии, где недавно были проведены реформы. Чарли беседует с местным бизнесменом по имени Фредо, и тот рассказывает, какие замечательные возможности получения прибыли он создал бы, если бы располагал достаточным капиталом. А затем он делает Чарли предложение: «Инвестируй в меня 100 000 долларов, и через год я превращу их в 500 000 долларов, которые мы с тобой поделим поровну. Следовательно, за год ты увеличишь свой капитал более чем в два раза». Возможность, о которой говорит Фредо, действительно очень заманчива, и Чарли охотно подписал бы соответствующий контракт в соответствии с законами Фридонии. Но насколько надежны эти законы? Если в конце года Фредо сбежит со всеми этими деньгами, сможет ли Чарли, уже находясь в Соединенных Штатах, подать на него иск о невыполнении договорных обязательств в суд Фридонии? Этот суд может или вынести предвзятое решение в пользу гражданина своей страны, или действовать слишком медленно, или его может подкупить Фредо. Все это означает, что Чарли предстоит сыграть с Фредо в игру, дерево которой показано на следующем рисунке. (Обратите внимание: если Фредо выполнит контракт, он выплатит Чарли 250 000 долларов; из этой суммы необходимо вычесть первоначальную инвестицию в размере 100 000 долларов. Следовательно, прибыль Чарли составит 150 000 долларов.)
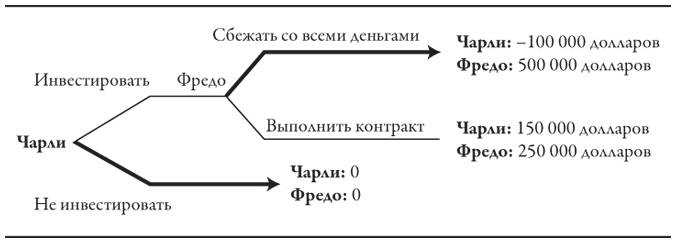
Как вы думаете, что сделает Фредо? При отсутствии понятных и веских причин верить его обещаниям Чарли должен предвидеть, что Фредо сбежит со всеми деньгами (подобно тому как маленькому Чарли следовало в свое время подумать о том, что Люси уберет мяч в сторону). Деревья этих двух игр на самом деле во многих отношениях идентичны. Однако сколько раз таким «чарли» не удавалось сделать правильные выводы в подобных ситуациях?
Какие у Чарли могут быть причины верить обещаниям Фредо? Возможно, он имеет отношение и ко многим другим предприятиям, которые нуждаются в финансировании из Соединенных Штатов или которым необходимо экспортировать свои продукты в США. В таком случае Чарли мог бы нанести Фредо ответный удар, разрушив его репутацию в Соединенных Штатах или добившись ареста его товаров. Следовательно, эта игра может быть частью более крупной игры, возможно, даже длительного взаимодействия, которое гарантирует честность Фредо. Однако если сделка носит разовый характер (как в показанном выше примере), логика обратных рассуждений очевидна.
Нам хотелось бы на примере этой игры подчеркнуть три важных момента. Во-первых, разные игры можно выразить в виде идентичных или очень похожих математических форм (деревьев или таблиц, подобных тем, что приведены в следующих главах). Использование формального математического представления позволяет провести параллели и перенести знания об игре из одной ситуации в другую. Это важная функция теории в любой предметной области: она дает возможность выделить существенные общие элементы на первый взгляд разных ситуаций, а также придерживаться унифицированного, а значит, более простого подхода к их анализу. Многим свойственно подсознательное неприятие теории как таковой. Но мы считаем, что это неправильно. Безусловно, у любой теории есть свои ограничения. Конкретные условия или события способны существенно дополнить или изменить рецепты, которые предоставляет теория. Однако если полностью отказаться от теории, можно лишиться ценной отправной точки для размышлений, а это серьезно затруднит решение проблемы. Нужно постараться сделать теорию игр своим помощником, а не препятствием в деле стратегического мышления.
Второй момент. Фредо должен понимать, что стратегически мыслящий Чарли отнесется к его предложению с недоверием и не станет вкладывать деньги, тем самым лишая его возможности заработать 250 000 долларов. Следовательно, у Фредо есть весомый стимул сделать свое обещание заслуживающим доверия. Будучи индивидуальным предпринимателем, Фредо почти не имеет влияния на слабую правовую систему страны, а значит, не может развеять подобные сомнения инвестора. Какие еще методы имеются в его распоряжении? Мы проанализируем вопрос достоверности стратегий и способы ее достижения в главах 6 и 7.
Третий и, вероятно, самый важный момент касается результатов, к которым придут участники игры в зависимости от того, какой вариант возможного развития событий выберут. Далеко не всегда складывается так, что, если один игрок получает больше, другой – непременно меньше. Ситуация, когда Чарли решает вложить деньги, а Фредо – выполнить контракт, более выгодна им обоим, чем ситуация, в которой Чарли не делает инвестиции. В отличие от соревнований или конкурсов, в таких играх нет победителей и проигравших; если говорить на языке теории игр, эти игры не должны быть играми с нулевой суммой. Они могут завершиться выигрышем или проигрышем обеих сторон. На самом деле в большинстве игр в бизнесе, политике и социальном взаимодействии присутствует как общность интересов (например, когда Чарли и Фредо могут оба получить прибыль, если Фредо найдет способ убедить партнера в том, что он выполнит контракт), так и конфликт интересов (в частности, если Фредо решит нажиться за счет Чарли и скрыться со всеми деньгами после того, как тот сделает инвестиции). Именно сочетание общности и конфликта интересов делает анализ таких игр столь интересным и актуальным.
Мы решили взять пример более сложного дерева игры из области политики. В одной из карикатур на американскую политику показано, что Конгресс США не прочь выделять средства из федерального бюджета на местные нужды, а президенты страны всячески стараются сокращать раздутые бюджеты, которые принимает Конгресс. Разумеется, у президентов есть свои предпочтения в отношении таких расходов, поэтому они хотели бы сокращать только те расходы, которые им не нравятся. Для этого им необходимо иметь право выборочного вето, которое предоставило бы им возможность сокращать расходы по отдельным статьям. В докладе «О положении в стране», представленном Конгрессу США в январе 1987 года, Рональд Рейган весьма красноречиво высказался по этому поводу: «Дайте нам тот инструмент, который есть у 43 губернаторов, – право постатейного вето, чтобы мы могли исключать бессмысленные проекты и привилегии, предоставляемые по политическим соображениям: все те статьи, которые сами по себе не уцелели бы».
На первый взгляд, право налагать вето на отдельные статьи законопроекта только укрепит власть президента и ни при каких обстоятельствах не приведет к негативным последствиям. Тем не менее существуют ситуации, в которых президенту лучше было бы обойтись без такого инструмента. Дело в том, что наличие у президента права выборочного вето повлияет на стратегию принятия законов, которой придерживается Конгресс. Простая игра покажет, как именно это может произойти.
Применительно к данной теме суть ситуации, сложившейся в 1987 году, сводилась к следующему. Предположим, на рассмотрение представлены две статьи расходов: модернизация городов («М») и система противоракетной обороны («П»). Конгрессу больше нравилось первое, тогда как президенту – второе. Тем не менее и Конгресс, и президент предпочли включить в законопроект обе эти статьи, а не сохранять статус-кво. В таблице отображена оценка возможных сценариев развития событий в случае двух игроков (4 – самая высокая оценка, 1 – самая низкая).

Дерево игры при условии, что у президента нет права выборочного вето, изображено на рисунке. Президент подпишет законопроект, в котором будут предусмотрены обе статьи – как М, так и П – или в котором будет только статья П, но наложит вето на законопроект, если в него будет включена только статья М. Зная об этом, Конгресс выбирает вариант с включением обеих статей. Мы снова показываем выбор, сделанный в каждом узле дерева, обозначив соответствующие варианты жирными линиями со стрелками. Обратите внимание: мы делаем это во всех тех точках, в которых президенту предположительно придется делать выбор, хотя некоторые варианты выбора поставлены под вопрос предыдущими решениями Конгресса. Дело в том, что выбор Конгресса в значительной мере зависит от анализа возможных шагов президента в случае, если бы Конгресс отдал предпочтение другому варианту. Для того чтобы проиллюстрировать эту логику, необходимо отобразить действия президента во всех возможных ситуациях.

Анализ этой игры позволяет сделать следующий вывод: в данном случае обе стороны посчитают нужным выбрать второй предпочтительный вариант (оценка 3).
Теперь предположим, что у президента есть право выборочного вето. В этом случае дерево игры будет выглядеть так:
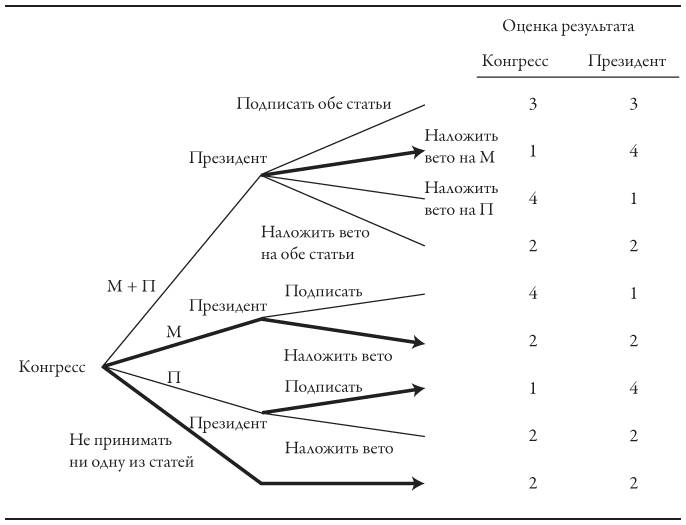
При этом Конгресс делает такой прогноз: в случае принятия обеих статей президент наложит вето на статью М и оставит только статью П. Следовательно, для Конгресса лучше всего либо принять только М и увидеть, как президент налагает вето на эту статью, или не принимать обе статьи. Возможно, Конгресс отдаст предпочтение первому варианту развития событий, если сможет извлечь политическую выгоду из вето президента. С другой стороны, президент тоже может извлечь для себя политическую выгоду из такого поддержания бюджетной дисциплины. Предположим, оба варианта уравновешивают друг друга, а это значит, что у Конгресса нет особых предпочтений в отношении того или иного выбора. Однако оба варианта дают каждой из сторон возможность получить результат, занимающий только третье место (оценка 2). Следовательно, даже президент может оказаться в затруднительном положении из-за наличия дополнительной свободы выбора[48].
Эта игра иллюстрирует важный концептуальный момент. В ситуации, когда решения принимает один человек, наличие большей свободы действий не принесет никакого вреда. Но в играх дополнительная свобода действий может навредить, поскольку способна повлиять на поведение других участников игры. Более того, связывание ваших же рук иногда идет на пользу. Такое «преимущество обязательства» рассматривается более подробно в главах 6 и 7.
Мы применили метод обратных рассуждений в очень простой игре (Чарли Браун), а затем использовали его в более сложной игре (выборочное вето). Основной принцип остается неизменным независимо от уровня сложности игры. Однако если речь идет об играх, в которых у каждого игрока в каждой точке принятия решений существует несколько вариантов выбора, дерево игры может очень быстро стать настолько сложным, что его будет трудно строить или использовать. Так, например, в шахматах из корневой вершины исходит 20 ветвей: шахматист, играющий белыми фигурами, может или передвинуть каждую из своих пешек на одну или две клетки, или сделать ход конем в одном из двух направлений. На каждый из этих ходов шахматист, играющий черными фигурами, может ответить 20 ходами. Следовательно, уже на этом уровне у нас имеется 400 разных путей. Число ветвей, исходящих из узлов на следующих уровнях, еще больше. Полное решение шахматной партии посредством построения дерева игры не под силу даже самому мощному компьютеру из всех, которые существуют в наше время или могут быть созданы в ближайшие несколько десятилетий. Следовательно, в таких случаях необходимо применять другие методы, такие как метод частичного анализа. Далее мы расскажем о том, как шахматисты решили эту проблему.
Между этими двумя крайними уровнями находятся игры среднего уровня сложности в таких областях, как бизнес, политика и повседневная жизнь. По отношению к таким играм можно использовать два подхода. Первый сводится к применению компьютерных программ для построения деревьев и расчета решений[49]. С другой стороны, многие игры среднего уровня сложности решаются посредством логического анализа дерева игры без построения самого дерева. Проиллюстрируем этот подход на примере игры в одном из ТВ-шоу, в котором каждый участник пытается «переиграть, перехитрить и продержаться дольше» всех остальных участников.
В реалити-шоу Survivor канала CBS можно найти много интересных стратегий. В одном из эпизодов «Survivor: Таиланд» две команды (или два племени) сыграли в игру, которая стала прекрасной иллюстрацией применения принципа «смотреть вперед и рассуждать в обратном порядке» в теории и на практике[50]. На игровом поле между племенами установили двадцать один флажок; члены каждого племени должны были по очереди убирать эти флажки. Когда наступала очередь одного из племен, его представитель мог убрать 1, 2 или 3 флажка. Убирать 0 флажков (иными словами, передавать свою очередь) не разрешалось, так же как убирать четыре или больше флажков за один раз. Побеждала команда, которая забирала последний флажок, если он оставался один, или все, если оставалось два или три[51]. Проигравшее племя должно было изгнать своего же представителя, что ослабляло позиции племени в будущих испытаниях. На самом деле проигрыш в данном случае сыграл решающую роль, и в итоге член другого племени выиграл главный приз – миллион долларов. Таким образом, способность выбрать правильную стратегию для этой игры была весьма ценной.
Участники шоу были разделены на два племени – Сук Джай и Чуай Ган; племя Сук Джай делало первый ход. В этом племени начали с того, что убрали 2 флажка, оставив на поле 19 флажков. Прежде чем читать дальше, сделайте небольшую паузу и подумайте: сколько флажков вы решили бы убрать на их месте?
Запишите где-нибудь ответ на этот вопрос и продолжайте читать. Для того чтобы понять, как следует играть в эту игру, и сопоставить правильную стратегию с тем, как на деле сыграли оба племени, обратите внимание на два показательных момента. Во-первых, перед началом игры оба племени получили по несколько минут на обсуждение этого испытания. Один из членов племени Чуай Ган, афроамериканец Тед Роджерс, который был разработчиком программного обеспечения, отметил: «В конце игры мы должны оставить их с четырьмя флажками». Это действительно так: оставшись с 4 флажками, племя Сук Джай должно убрать 1, 2 или 3 флажка. В таком случае племени Чуай Ган останется только дождаться своей очереди, убрать 3, 2 или 1 флажок соответственно – и победить. В племени Чуай Ган правильно поняли и использовали эту возможность: когда оставалось 6 флажков, они убрали два из них.
Но есть еще один показательный момент. На предыдущем ходе, когда племя Сук Джай забрало 3 флажка из оставшихся 9, одна из представительниц этого племени Ши Энн, которая умела четко формулировать мысли и по праву гордилась своими аналитическими способностями, вдруг осознала: «Если Чуай Ган возьмет два флажка, нам конец». Это означало, что племя Сук Джай только что сделало неправильный ход. Что же следовало делать дальше в этой ситуации?
Ши Энн или одному из ее соплеменников следовало бы размышлять так же, как это сделал Тед Роджерс, и попытаться оставить другое племя с четырьмя флажками, но применив эту логику к следующему ходу этого племени. Как оставить другое племя с 4 флажками на его следующем ходе? Оставив его с 8 флажками на предыдущем! Когда это племя заберет 1, 2 или 3 флажка из восьми, вы возьмете 3, 2 или 1 флажок, оставив его с четырьмя флажками, как и планировали. Следовательно, племени Сук Джай необходимо было бы поменяться местами с племенем Чуай Ган и взять только 1 флажок из 9. Аналитический ум Ши Энн начал активно работать, но с опозданием на один ход! По всей видимости, у Теда Роджерса аналитические способности были еще лучше. Но так ли это?
Почему племя Сук Джай оказалось с 9 флажками на предыдущем ходе? Потому что в Чуай Ган убрали с поля 2 флажка из 11 на своем предыдущем ходе. Теду Роджерсу следовало продолжить свои рассуждения на один ход дальше. Племени Чуай Ган нужно было забрать 3 флажка, оставив Сук Джай с 8 флажками – а это проигрышная позиция.
Эти же рассуждения можно продолжить в обратном порядке. Для того чтобы оставить другое племя с 8 флажками, вам следует оставить его с 12 флажками на предыдущем ходе; для этого необходимо оставить его с 16 флажками на ход раньше и с 20 флажками на ход до этого хода. Таким образом, племени Сук Джай следовало начать игру, убрав с игрового поля только 1 флажок, а не 2, как случилось на самом деле. Такой ход обеспечил бы этому племени неизбежную победу, оставив племя Чуай Ган с 20, 16, … 4 флажками на очередных ходах[52].
А теперь вспомним первый ход племени Чуай Ган. У них было 19 флажков. Если бы в Чуай Ган придерживались своей же логики, им следовало взять 3 флажка, оставив Сук Джай с 16 флажками и тем самым обрекая это племя на неизбежное поражение. Начиная с любого этапа игры, на котором соперник произвел неправильный ход, команда, делавшая очередной ход, могла перехватить инициативу и выиграть. Но племя Чуай Ган тоже играло не идеально[53].
В таблице показаны как фактические, так и правильные ходы обоих племен на каждом этапе игры. (Запись «Нет хода» означает, что любой ход проигрышный при условии, что соперник делает правильный ход.) Из этой таблицы видно, что практически во всех случаях оба племени делали неправильный выбор. Исключением стал только ход племени Чуай Ган, когда они оказались с 14 флажками, но даже он, скорее всего, был случайным, поскольку на следующем ходе племя убрало с поля 2 флажка из 11, тогда как следовало взять 3 флажка.
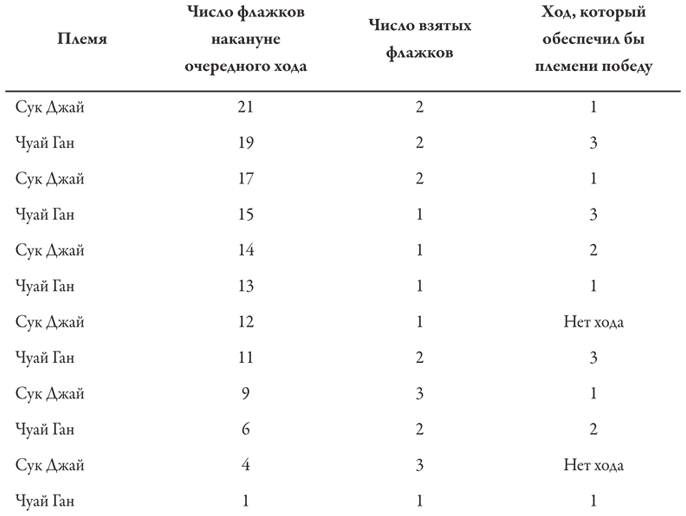
Не судите эти племена слишком строго: для того чтобы научиться играть даже в самые простые игры, требуются время и опыт. На своих занятиях мы проводили эту игру парами или в группах студентов и пришли к выводу, что даже студентам первого курса университетов Лиги плюща[54] требуется сыграть три или даже четыре раунда, прежде чем они полностью усвоят логику игры и начнут играть правильно с первого хода. (Кстати, какое число флажков выбрали вы, когда мы попросили вас сделать это, и как аргументировали этот выбор?) Следует отметить, что люди обучаются быстрее, когда наблюдают за игрой со стороны, чем когда играют сами. Возможно, позиция наблюдателя позволяет увидеть общую картину игры и строить свои рассуждения более спокойно, чем в роли участника.
Для того чтобы помочь вам лучше понять логику рассуждений в этой игре, предлагаем первую задачу для тренировки мышления (такие задачи помогут вам отработать навыки стратегического мышления). Ответы вы сможете найти в конце книги, в разделе «Решения».
ЗАДАЧА ДЛЯ ТРЕНИРОВКИ МЫШЛЕНИЯ № 1
Позвольте нам изменить правила игры на прямо противоположные: теперь вы выиграете, если заставите другую команду взять последний флажок. Сейчас ваш ход, и у вас 21 флажок. Сколько флажков вы возьмете?
Теперь, когда вы укрепили свое мышление, решив эту задачу, рассмотрим другие элементы стратегии, которая применяется в играх данного класса.
У игры с флажками было одно свойство, которое делало ее полностью разрешимой, – это отсутствие неопределенности любого вида, будь она обусловлена естественным элементом случайности, мотивами и возможностями других игроков или их фактическими действиями. На первый взгляд, это довольно простая идея, и все-таки она требует уточнения и разъяснения.
Во-первых, на любом этапе игры, когда племя должно было сделать свой ход, ему были известны все условия игры, в частности, сколько осталось флажков. Во многих других играх присутствует элемент чистой случайности, которую создает сама природа или боги случайностей. Например, во многих карточных играх дело обстоит так: когда игрок принимает решение, он не знает наверняка, какие карты на руках у других игроков, хотя может делать какие-то предположения на основании их предыдущих действий. В следующих главах рассматриваются игры, в которых присутствует естественный элемент случайности.
Во-вторых, племени, которому предстояло сделать выбор, была известна цель другого племени – одержать победу. Чарли Брауну тоже следовало бы знать, что Люси нравится наблюдать за тем, как он падает на спину. Игроки точно знают цели другого игрока или игроков во многих простых играх и спортивных соревнованиях, но так бывает далеко не всегда в играх, которые люди ведут в бизнесе, политике и в процессе социального взаимодействия. В таких играх мотивы игроков представляют собой сложное сочетание эгоизма и альтруизма, стремления к честности и справедливости, краткосрочных и долгосрочных соображений и так далее. Для того чтобы понять, какой выбор сделают другие игроки на следующих этапах игры, необходимо знать их цели, а если таких целей несколько – какова их приоритетность. Вы можете так и не узнать об этом, поэтому вам придется делать обоснованные предположения. Не стоит думать, что у других людей такие же предпочтения, как у вас или у гипотетического «человека рационального», но вы должны тщательно проанализировать их ситуацию. Поставить себя на место другого человека – достаточно трудная задача, которую часто усложняет ваша эмоциональная привязанность к своим целям и стремлениям. Более подробно на неопределенности данного вида мы остановимся далее в этой главе, а также в других главах книги. Пока же просто обращаем ваше внимание на то, что неопределенность мотивов других игроков – это именно тот вопрос, с которым целесообразно обратиться к независимой третьей стороне – консультанту по вопросам стратегии.
И последнее: участники многих игр сталкиваются с неопределенностью выбора других игроков, которую иногда обозначают термином «стратегическая неопределенность», для того чтобы отличить ее от неопределенности, обусловленной естественной случайностью (как в случае раздачи карт или отскока мяча из-за неровностей поля). В игре с флажками не было стратегической неопределенности, поскольку каждое племя точно знало, какой предыдущий ход сделало другое племя. Однако во многих других случаях игроки действуют одновременно или в такой быстрой последовательности, что один не успевает увидеть ход другого и сделать адекватный ответный ход. В футболе вратарь, которому предстоит отбить пенальти, должен принять решение, в какую сторону двигаться – направо или налево, хотя он не знает заранее, куда прицелится игрок, который будет выполнять пенальти. Хороший футболист до последней микросекунды пытается обмануть вратаря, чтобы у того не осталось времени предпринять необходимые действия. То же самое можно сказать о подачах и обводящих ударах в теннисе и во многих других играх. Каждый участник закрытого аукциона должен принимать решения, не зная о том, какой выбор делают остальные. Иными словами, во многих играх игроки делают ходы одновременно, а не в заранее заданной последовательности. Процесс размышлений, на основании которого участникам таких игр приходится делать свой выбор, в некоторых отношениях более сложен, чем метод обратных рассуждений в играх с последовательными ходами (как игра с флажками): каждый игрок должен понимать, что другие делают осознанный выбор и, в свою очередь, анализируют, как размышляет он, и так далее. В следующих главах пойдет речь о том, как выстроить рассуждения и какими инструментами решения воспользоваться для игр с параллельными ходами. В данной же главе сосредоточимся исключительно на играх с последовательными ходами, к которым относится игра с флажками, а также более сложная игра – шахматы.
Построение обратных рассуждений по дереву игры – это правильный подход к анализу и решению игр, в которых игроки делают ходы поочередно. Тот, кто не делает этого (неважно, осознанно или нет), препятствует достижению собственных целей; таким людям следует прочитать нашу книгу или нанять консультанта по вопросам стратегии. Однако это рекомендуемый или стандартный вариант применения метода обратных рассуждений. Имеет ли этот метод определенную эксплицитную или положительную ценность, подобно большинству других научных методов? Иными словами, дает ли применение этого метода правильные результаты в играх, разыгрывающихся в реальной жизни? Исследователи, которые занимаются новыми, увлекательными областями поведенческой экономики и поведенческой теории игр, провели эксперименты, которые позволяют сделать противоречивые выводы.
Самые серьезные критические аргументы возникают в связи с игрой в ультиматум. Это простейшая игра по ведению переговоров, в которой делается только одно ультимативное предложение. В игре принимают участие два игрока: делающий предложение (игрок А) и отвечающий на предложение (игрок Б) – и некая сумма денег, скажем, 100 долларов. Игрок А начинает игру, предлагая игроку Б разделить 100 долларов между ними двумя. Игрок Б решает, стоит ли ему принимать предложение игрока А. Если Б соглашается, деньги делятся на части в соответствии с предложением игрока А, каждый игрок получает соответствующую сумму и игра заканчивается. Если игрок Б не принимает предложение, оба игрока не получают ничего и игра тоже заканчивается.
Сделайте паузу и подумайте. Если бы вы играли в эту игру в роли игрока А, как бы вы предложили разделить деньги?
Теперь поразмыслите над тем, как в эту игру сыграли бы два человека, которые поступают рационально с точки зрения классической экономической теории – иными словами, если бы каждый заботился только о собственных интересах и смог бы правильно просчитать оптимальную стратегию их удовлетворения. Игрок, делающий предложение (А), думал бы так: «Как бы я ни предложил разделить деньги, у Б одна альтернатива: получить предложенную сумму или остаться ни с чем. (Игра проводится только один раз, поэтому Б нет смысла создавать себе репутацию несговорчивого человека или отвечать на действия игрока А той же монетой.) Это означает, что Б примет любое мое предложение. Мне выгоднее всего предложить Б как можно меньше, например один цент, если это позволяют правила игры». Следовательно, игрок А предложил бы Б минимальную сумму, а игрок Б принял бы это предложение[55].
Сделайте еще одну паузу и подумайте. Если бы вы играли в эту игру в роли игрока Б, приняли бы один цент?
Ультимативная игра стала объектом многочисленных экспериментов[56]. Как правило, в ходе таких экспериментов в одном месте собирают около двух десятков человек и в произвольном порядке разбивают их по парам. В каждой паре распределяются роли игрока, делающего предложение, и игрока, отвечающего на предложение. Новые пары тоже формируются в случайном порядке, и игра начинается снова. В большинстве случаев игроки не знают, с кем они будут играть в очередном раунде. Благодаря такому подходу экспериментатор получает несколько наборов данных, работая с одной группой участников эксперимента на протяжении одного сеанса, но при этом отсутствует возможность формирования устойчивых связей, которые могут повлиять на поведение участников эксперимента. В рамках этой общей схемы создаются различные варианты условий, с тем чтобы изучить их влияние на конечный результат.
В этом варианте ультимативной игры игрок А делает предложение игроку Б, как разделить 100 долларов. Если Б принимает предложение А, они делят деньги и игра заканчивается. Но если Б говорит «нет», А должен решить, делать ли еще одно предложение. Каждое очередное предложение игрока А должно быть более щедрым. Игра заканчивается, когда игрок Б принимает предложение или когда игрок А прекращает делать предложения. Как вы думаете, каким будет итог этой игры?
В данном случае можем предположить, что игрок А будет делать предложения до тех пор, пока не предложит игроку Б 99 долларов, оставив себе 1 доллар. Таким образом, согласно древовидной логике обратных рассуждений, игрок Б получит почти все деньги. Если бы вы были игроком Б, стали бы вы держаться до того момента, когда А предложит вам поделить деньги по принципу 99:1? Советуем не делать этого.
По всей вероятности, ваш собственный анализ того, как вы действовали бы в роли первого и второго игроков, дает вам основания предположить, что в реальной жизни результаты этой игры должны отличаться от представленных теоретических прогнозов. И они действительно отличаются, причем во многих случаях существенно. Игроки, которые делают предложение, делят деньги по-разному, но один цент, один доллар или любую другую сумму ниже 10 процентов от суммы, стоящей на кону, называют крайне редко. Средняя сумма (половина игроков предлагают больше этой суммы, половина – меньше) находится в диапазоне от 40 до 50 процентов; во многих экспериментах чаще всего встречается деление 50:50. Игроки, отвечающие на предложения, в половине случаев отвергают те из них, которые обеспечивают им менее 20 процентов от общей суммы.
Почему игроки предлагают достаточно большую долю от общей суммы тем, кто принимает предложения? Здесь вероятны три причины. Во-первых, не исключено, что игрок, делающий предложение, не владеет методом обратных рассуждений. Во-вторых, у предлагающих игроков могут быть и другие мотивы, отличные от сугубо эгоистичного желания получить по максимуму: например, альтруистические побуждения или чувство справедливости. В-третьих, они могут опасаться, что игроки, которым они делают предложение, откажутся от предложенной суммы, если она будет слишком маленькой.
Первая причина маловероятна, поскольку логика обратных рассуждений в этой игре совсем нетрудная. В более сложных ситуациях игроки не всегда в состоянии корректно выполнить все необходимые расчеты, особенно если они новички в этой игре (как мы уже видели в игре с флажками). Но ультимативная игра достаточно проста даже для новичков. Следовательно, этот феномен можно объяснить второй причиной, третьей причиной или их сочетанием.
Первые результаты экспериментов с ультимативной игрой свидетельствовали в пользу третьей причины. Профессор Гарвардского университета Эл Рот и его коллеги пришли к выводу, что в той схеме формирования порога отказов, которая преобладала в их группе испытуемых, предлагающие игроки выбирали свои предложения таким образом, чтобы достичь оптимального соотношения перспективы получения большей доли для себя и риска отказа со стороны отвечающего игрока. Это говорит о наличии незаурядной традиционной рациональности у игроков, делающих предложения.
Однако более поздние исследования, посвященные различиям между второй и третьей возможностями, позволили сделать другие выводы. Для того чтобы разграничить альтруизм и стратегию, были проведены эксперименты с использованием одного из вариантов ультимативной игры – игры в диктатора. В этой игре первый игрок диктует, как должна быть разделена имеющаяся сумма денег; другой должен принять это предложение, каким бы оно ни было. В игре в диктатора предлагающие игроки в среднем отдают существенно меньше, чем в обычной ультимативной игре, но все же они отдают гораздо больше ноля. Следовательно, доля истины есть в обоих объяснениях: поведение предлагающего игрока в ультимативной игре обусловлено как щедростью, так и стратегией.
Однако чем именно вызвана эта щедрость – альтруизмом или соображениями справедливости? Оба объяснения – разные аспекты того, что можно было бы назвать свойственной людям заботой о других. Понять разницу между ними позволяет такое исследование. В эксперименте, который проводится по обычной схеме, после формирования пар роли предлагающего и отвечающего игроков распределяются одним из методов случайного выбора, например подбрасыванием монеты. Благодаря этому у игроков может возникнуть ощущение равенства или справедливости. Для того чтобы исключить этот элемент, роли распределяются посредством предварительного испытания, такого как тест на общий уровень знаний. Победитель становится игроком, который будет делать предложения, воспринимая это как должное, что приводит к снижению предлагаемых сумм в среднем на 10 процентов. Тем не менее предложения по-прежнему остаются гораздо больше ноля, а это говорит о том, что в рассуждениях предлагающих игроков присутствует элемент альтруизма. Не забывайте о том, что они не знакомы лично с отвечающими игроками, поэтому здесь речь идет об альтруизме вообще, а не о заботе о благополучии конкретного человека.
Возможен и третий вариант индивидуальных предпочтений: игрок, который делает предложения, определяя размер предлагаемой суммы, может руководствоваться чувством стыда. Джейсон Дана из Пенсильванского университета, Дейлиен Кейн из Школы менеджмента Йельского университета и Робин Доуз из Университета Карнеги-Меллона провели эксперимент со следующим вариантом игры в диктатора[57]. Диктатору предлагают выделить другому игроку 10 долларов. После того как эта сумма выделена, но прежде, чем она уйдет к другому игроку, диктатору делают такое предложение: он может получить 9 долларов, другой игрок не получит ничего, но он даже не узнает, что принимал участие в эксперименте. Большинство диктаторов принимают это предложение. Следовательно, они готовы отдать один доллар за то, чтобы другой игрок не узнал об их жадности. (Альтруист предпочел бы оставить себе 9 долларов и отдать другому игроку 1 доллар, а не оставлять себе 9 долларов при условии, что другой человек не узнает об этом.) Даже если бы диктатору предложили 3 доллара, он все равно взял бы эти деньги, лишь бы другой игрок оставался в неведении. Это напоминает ситуацию, когда человек готов перейти на другую сторону улицы, лишь бы не подавать милостыню нищему.
Обратите внимание на два следующих аспекта этих экспериментов. Во-первых, они проводятся в полном соответствии со стандартной научной методикой: истинность гипотез проверяется посредством создания приемлемых вариантов контроля в этих экспериментах. Мы приводим здесь несколько самых интересных. (В книге Колина Камерера, ссылку на которую можно найти в примечаниях к главе 2, рассматриваются другие варианты.) Во-вторых, социальные науки допускают сосуществование множества разных причин, что объясняет отдельные аспекты одного и того же феномена. Гипотезы не должны быть ни абсолютно правильными, ни полностью ошибочными; принять одну гипотезу – это не значит отбросить все остальные.
А теперь проанализируйте поведение игроков, отвечающих на предложение. Почему они отказываются, даже если знают, что единственная альтернатива – получить еще меньше? Причина не может быть в том, что они стремятся создать себе репутацию жестких переговорщиков, которая может принести свои плоды в будущих раундах этой игры или в других играх на разделение. Одна и та же пара не играет повторно, а будущие партнеры не имеют доступа к данным о прошлых действиях того или иного игрока. Следовательно, даже если такой мотив, как репутация, присутствует неявно, он принимает более глубокую форму и выступает в качестве общего принципа действий, которого придерживается отвечающий игрок без каких бы то ни было явных рассуждений и расчетов в каждом конкретном случае. Он действует инстинктивно или отвечает на предложение под влиянием эмоций. И это действительно так. В новом направлении экспериментальных исследований под названием «нейроэкономика» деятельность мозга испытуемых во время принятия различных экономических решений фиксируется с помощью функциональной магнитно-резонансной томографии (functional magnetic resonance imaging – fMRI) и позитронно-эмиссионной томографии (positron emission tomography – PET). При этом у отвечающих игроков наблюдается более высокая активность передней части островковой коры головного мозга, когда предложения первого игрока становятся более несправедливыми. Поскольку передняя часть островковой коры более активно реагирует на эмоции (такие как гнев или недовольство), полученный результат помогает объяснить, почему игроки, делающие второй ход, отклоняют несправедливые предложения. Напротив, левая часть префронтальной коры активизируется, когда игрок принимает несправедливое предложение, а это говорит о том, что в такой момент он осознанно контролирует свои действия, пытаясь найти оптимальное соотношение между стремлением выразить свое недовольство и желанием получить больше денег[58].
Многие люди (особенно экономисты) заявляют, что, хотя игроки, отвечающие на предложение, действительно отказываются от маленькой доли небольших сумм, которые предлагают им в ходе лабораторных экспериментов, в реальном мире, где ставки зачастую гораздо выше, вероятность отказа крайне низка. Для того чтобы проверить это утверждение, исследователи провели эксперименты с ультимативными играми в бедных странах, где поставленная на кон сумма равнялась доходу участников экспериментов за несколько месяцев. Число отказов действительно несколько сократилось, но предложения не стали существенно менее щедрыми. Последствия отказа стали более серьезными как для игроков, делающих предложения, так и для игроков, отвечающих на них, поэтому предлагающие игроки, опасающиеся отказа, начали вести себя более осмотрительно.
Поведение человека можно отчасти объяснить присущими ему инстинктами, гормонами или эмоциями, однако некоторые аспекты поведения зависят также от культурной принадлежности. В ходе экспериментов, которые проводились в разных странах, был обнаружен интересный факт. Понятия о том, что можно считать разумным предложением, отличались в разных культурах почти на 10 процентов, хотя представления о таких качествах, как агрессивность и жесткость, разнились в меньшей степени. Результаты экспериментов существенно отличались от остальных только в одной группе: в племени мачигенга, обитающем в районе перуанской Амазонки, предложения были намного меньше (в среднем 26 процентов) и только одно было отклонено. Антропологи объясняют это тем, что племя мачигенга состоит из небольших семейств, оно социально изолировано и в нем нет сложившихся норм распределения материальных благ. Напротив, в двух культурах предложения превышали 50 процентов; в этих культурах сформировалась традиция делать щедрые пожертвования, когда кому-то выпадает удача (такая традиция возлагает на получателя дара обязанность отплатить в будущем еще более щедрым пожертвованием). Эта норма или обычай переносится и на эксперимент, хотя игроки даже не знают, кому они отдают деньги или от кого их получают[59].
Какой вывод следует из результатов этих экспериментов с ультимативными играми, а также других подобных экспериментов? Во многих случаях эти результаты существенно отличаются от того, на что можно было бы рассчитывать, полагаясь на метод обратных рассуждений и предположение о том, что каждый игрок заботится только о собственной выгоде. Что именно можно назвать ложным предположением – способность игроков корректно выполнить обратные рассуждения, или их эгоизм, или сочетание того и другого? И каковы возможные последствия?
Для начала проанализируем метод обратных рассуждений. Мы видели, что участники реалити-шоу Survivor не смогли корректно применить этот метод в игре с флажками. Они играли в эту игру впервые, но даже несмотря на это, в обсуждении игры обнаружились проблески правильных рассуждений. Как показывает наш опыт, студенты полностью осваивают стратегию игры, сыграв в нее или понаблюдав за ней всего три-четыре раза. Многие экспериментаторы неизменно и практически намеренно работают с новичками, которые в большинстве случаев только учатся играть в ту или иную игру. В реальном мире бизнеса, политики и профессионального спорта, где люди имеют достаточно богатый опыт в тех играх, в которые им приходится играть, мы должны быть готовыми к тому, что у игроков гораздо больше знаний и что они чаще всего используют правильные стратегии, выбранные либо после тщательного взвешивания возможных вариантов, либо с помощью интуиции, опирающейся на знания. В более сложных играх стратегически грамотные игроки могут воспользоваться компьютерами или помощью консультантов для выполнения необходимых расчетов; сейчас такая практика встречается достаточно редко, но вскоре получит более широкое распространение. Именно поэтому мы убеждены в том, что метод обратных рассуждений должен оставаться нашей отправной точкой для анализа подобных игр и прогнозирования их результатов. При необходимости первые попытки анализа игры можно привести в соответствие с конкретным контекстом, поскольку начинающие могут допускать ошибки, а некоторые игры слишком сложны для того, чтобы их можно было решить без посторонней помощи.
По нашему глубокому убеждению, из этих экспериментальных исследований можно извлечь более важный урок: люди делают свой выбор, руководствуясь не только собственной выгодой, но и другими соображениями и предпочтениями. Это выводит нас за рамки классической экономической теории. Специалисты по теории игр должны учитывать, какое значение придают справедливости и альтруизму участники той или иной игры. «Поведенческая теория игр скорее раздвигает границы рациональности, а не отбрасывает ее»[60].
Все это к лучшему: понимание мотивов, которыми руководствуются люди, углубляет наше понимание процесса принятия экономических решений, а также процесса стратегического взаимодействия. И это уже происходит: передовые исследования в области теории игр все чаще учитывают такие цели игроков, как справедливость, альтруизм и другие стремления подобного рода (и даже «вторичное» стремление вознаградить или наказать других участников игры, поведение которых отображает или нарушает эти принципы)[61].
Однако мы не должны останавливаться на этом; мы должны сделать следующий шаг и поразмышлять над тем, почему людям свойственно стремление к альтруизму и справедливости, а также почему они часто испытывают такой сильный гнев и возмущение, когда кто-то нарушает эти принципы. Это уводит нас в область предположений, однако одно правдоподобное объяснение можно найти в эволюционной психологии. В группах, члены которых придерживаются таких норм поведения, как справедливость и альтруизм, меньше внутренних конфликтов, чем в группах, которые состоят из эгоистичных индивидов. Следовательно, подобные группы смогут добиться более весомых успехов в коллективных действиях, включая создание материальных благ, которые приносят пользу всей группе, и рациональное использование общих ресурсов. Кроме того, они тратят меньше усилий и ресурсов на внутренние конфликты. В итоге эти группы добиваются большего как в абсолютном выражении, так и в конкуренции с группами, в которых отсутствуют такие нормы поведения. Иными словами, определенная мера справедливости и альтруизма может иметь эволюционную ценность с точки зрения выживания.
Некоторые биологические основания для отказа от несправедливых предложений определились в ходе эксперимента, который провел Терри Бернхем[62]. В его версии ультимативной игры на кону было 40 долларов, а в качестве испытуемых выступали студенты магистратуры Гарвардского университета. У игрока, которому предстояло разделить эту сумму, было только два варианта: предложить другому игроку 25 долларов и оставить себе 15 долларов или предложить 5 долларов и оставить себе 35 долларов. Из тех, кому предложили всего 5 долларов, двадцать студентов приняли это предложение, а шесть отклонили, из-за чего и они сами, и игроки, делившие сумму, не получили ничего. А теперь самое главное. Оказалось, что у шести студентов, которые отказались принять предложение, уровень тестостерона был на 50 процентов выше, чем у тех, кто его принял. Поскольку уровень тестостерона определяет, как человек воспринимает свой статус и насколько агрессивным он может быть, возможно, это и есть генетическая причина эволюционного преимущества того, что биолог-эволюционист Роберт Трайверс назвал «моральной агрессией».
Кроме возможных генетических факторов, в любом обществе существуют негенетические способы передачи норм поведения, в частности, процесс обучения и социализации детей в семьях и в школах. Родители и учителя рассказывают восприимчивым детям, как важно заботиться о других людях, делиться с другими и вести себя хорошо. Безусловно, некоторые из этих убеждений навсегда остаются в сознании детей и оказывают влияние на их поведение на протяжении всей их жизни.
В заключение должны отметить, что справедливость и альтруизм имеют свой предел. В долгосрочной перспективе прогресс и успехи общества немыслимы без инноваций и перемен, а они в свою очередь невозможны без индивидуализма и готовности нарушить социальные нормы и отбросить устоявшиеся стереотипы; этим качествам часто сопутствует эгоизм. Следовательно, необходим баланс между заботой о себе и заботой о других.
Когда вы приобретете некоторый опыт в применении метода обратных рассуждений, то поймете, что его можно использовать во многих стратегических ситуациях в повседневной жизни или в работе даже без построения деревьев. Многие другие игры средней степени сложности решаются посредством специальных компьютерных программ, которые становятся все более доступными для широкого применения. Однако в сложных играх (таких как шахматы) найти полное решение методом обратных рассуждений невозможно.
Теоретически шахматы – это игра, которая идеально подходит для обратных рассуждений, поскольку она состоит из серии последовательных ходов[63]. Игроки делают свои ходы поочередно; за всеми ходами можно наблюдать, и их нельзя отменить; нет никакой неопределенности в отношении позиции или мотивов игроков. Правило, согласно которому в случае повторения одной и той же позиции объявляется ничья, гарантирует завершение партии за конечное число ходов. Мы можем начать с листьев дерева (или концевых вершин) и анализировать игру в обратном направлении. Однако теория и практика – это две разные вещи. Было подсчитано, что общее число вершин дерева игры в шахматах составляет около 10120, то есть 1 с 120 нолями. Сверхмощному компьютеру, быстродействие которого в 1000 раз превышает быстродействие обычного персонального компьютера, понадобилось бы 10103 лет на то, чтобы проанализировать все возможные ходы по такому дереву. Ждать так долго бессмысленно, а прогнозируемое развитие компьютерной техники в обозримом будущем вряд ли существенно улучшит ситуацию. Так какой же выход нашли шахматисты и программисты?
Специалистам по шахматам удалось описать оптимальные стратегии на последних этапах игры. Когда на шахматной доске остается небольшое число фигур, специалисты могут заглянуть в конец игры и методом обратных рассуждений установить, гарантирована ли победа одной стороне или другая сторона может добиться ничьей. Но в середине шахматной партии, когда на доске остается еще достаточно много фигур, определить возможное развитие событий гораздо труднее. Хорошие шахматисты могут просчитать наперед около пяти пар ходов, но это не позволит упростить ситуацию до уровня, который позволил бы уже на этом этапе разыграть правильную стратегию эндшпиля.
Практическое решение этой проблемы сводится к применению двух подходов: анализа ходов методом обратных рассуждений и субъективной оценки шахматной позиции. Первый – это наука, теория игры: умение смотреть вперед и рассуждать в обратном порядке; второй подход – искусство специалиста-практика: способность определить ценность шахматной позиции по числу оставшихся фигур и взаимодействию между ними без определения явно выигрышной стратегии игры с этого момента. Шахматисты часто называют этот феномен «знанием», но вы можете называть это опытом, интуицией или искусством. Лучших шахматистов отличает, как правило, глубина и тонкость знания.
Такое знание можно накопить, наблюдая за многими шахматными партиями и многими игроками, после чего составить свод правил игры. Большая работа в этом плане уже проведена в отношении дебюта, или первых десяти-пятнадцати ходов. Существуют сотни книг, в которых анализируются разные дебюты и обсуждаются их преимущества и недостатки.
Какова роль компьютеров во всем этом? Было время, когда проект написания программ, которые позволили бы компьютеру играть в шахматы, считался неотъемлемой частью новой области науки – искусственного интеллекта, цель которой состояла в создании компьютеров, способных мыслить подобно человеку. Но за многие годы этого так и не удалось добиться, поэтому ученые стали уделять все больше внимания тому, что компьютеры делают лучше всего, – математическим вычислениям. Компьютеры просчитывают наперед больше ходов и делают это быстрее, чем люди[64]. Опираясь на одни только математические вычисления, в конце 1990-х годов специальные шахматные компьютеры, такие как Fritz и Deep Blue, смогли соперничать с лучшими шахматистами.
Рейтинг шахматистов определяется по результатам игр; рейтинг лучших шахматных компьютеров сопоставим с рейтингом 2800, который имеет сильнейший шахматист мира Гарри Каспаров. В ноябре 2008 года Каспаров сыграл матч из четырех партий с последней версией компьютера Fritz – X3D. В итоге в двух партиях каждая из сторон одержала победу, а две партии завершились вничью. В июле 2005 года шахматный компьютер Hydra нанес полное поражение Майклу Адамсу, который занимал 13-е место в рейтинге лучших шахматистов мира: пять партий компьютер выиграл, а одна завершилась вничью. Возможно, не за горами то время, когда компьютерные программы займут первые места в рейтинге и начнут играть друг с другом на чемпионатах мира по шахматам.
Какие выводы следуют из этой истории о шахматах? Она показывает, каким должен быть ход размышлений в любых играх высокого уровня сложности, с которыми вы можете столкнуться. Необходимо объединить принцип «смотреть вперед и рассуждать в обратном порядке» с опытом, который поможет вам оценить промежуточные позиции, достигнутые к концу периода предварительных расчетов. Вы сможете добиться успеха только благодаря такому синтезу науки под названием «теория игр» и искусства ведения конкретной игры, а не с помощью каждого из этих элементов в отдельности.
Стратегия игры в шахматы иллюстрирует еще один важный аспект метода обратных рассуждений: вы должны вести игру с точки зрения обоих игроков. Просчитать лучший ход в сложной игре очень трудно, но еще труднее предвидеть, что сделает другой игрок.
Если бы у вас действительно была возможность просчитать все возможные ходы и контрходы и то же самое мог бы сделать другой игрок, то вы могли бы заранее договориться о том, чем завершится игра. Но поскольку ваши возможности анализа ограничены несколькими ветвями дерева игры, другой игрок может видеть то, чего вы не видите, или упустить то, что очевидно для вас. Как бы там ни было, ваш соперник может сделать ход, которого вы не предвидели.
Для эффективного применения правила «смотреть вперед и рассуждать в обратном порядке» необходимо предвидеть, что сделает на самом деле другой игрок, а не то, что сделали бы на его месте вы. Проблема состоит в том, что, когда вы пытаетесь встать на место другого игрока, очень трудно и даже невозможно забыть о том, в какой ситуации находитесь вы сами. Вы слишком много знаете о том, что планируете сделать на следующем этапе игры, и вам трудно не поддаваться влиянию этих знаний, когда вы анализируете игру с точки зрения другого игрока. Это объясняет, почему в шахматах (или в покере) никто не играет сам с собой: невозможно блефовать или сделать неожиданный ход против себя самого.
У этой проблемы нет идеального решения. Пытаясь поставить себя на место другого игрока, вы должны знать, что знает он, и не знать о том, чего он не знает. Цели другого игрока должны стать вашими целями, а не соответствовать вашим ожиданиям по этому поводу. На практике компании, которые пытаются просчитать ходы и контрходы конкурентов в том или ином сценарии развития бизнеса, нанимают сторонних специалистов на роль другой стороны. Так они могут быть уверены в том, что их партнерам по игре известно не так уж много. Во многих случаях полезнее всего выделить те ходы соперника, которых вы не ожидали, и проанализировать, что привело к такому результату, с тем чтобы впоследствии можно было либо попытаться избежать такого развития событий, либо способствовать ему.
В заключение этой главы вернемся к Чарли Брауну и его попыткам решить вопрос, бить или не бить по мячу. Этот вопрос стал настоящей проблемой для футбольного тренера Тома Осборна в последние минуты борьбы его команды за звание чемпиона. Мы считаем, что он тоже принял неправильное решение. Метод обратных рассуждений поможет нам понять, в чем он ошибся.
В 1984 году состоялся матч кубка по студенческому американскому футболу Orange Bowl («Апельсиновый кубок») между командой Nebraska Cornhuskers («Кукурузники Небраски»), не потерпевшей ни одного поражения, и командой Miami Hurricanes («Ураганы Майами»), которая проиграла только один матч. Поскольку накануне финального матча результаты команды Небраски были лучше, ей достаточно было сыграть вничью, чтобы завершить сезон, заняв первое место.
В начале четвертого периода команда Небраски проигрывала со счетом 31:17. Затем Cornhuskers начали сокращать разрыв. Они заработали тачдаун, после чего счет стал 31:23. Тренеру команды из Небраски Тому Осборну предстояло принять важное стратегическое решение.
В студенческом футболе команда, которая зарабатывает тачдаун, получает право продолжить игру с линии, расположенной в 2,5 ярдов от очковой зоны. У команды есть два варианта дальнейших действий: либо доставить мяч в очковую зону (забежав в нее или передав пас игроку, который уже находится в ней) и заработать еще 2 очка, либо применить менее рискованную стратегию, забив гол – это дает одно дополнительное очко.
Тренер Осборн выбрал более безопасную стратегию, и команда Небраски забила гол, заработав одно очко. Теперь счет был 31:24. Команда Cornhuskers продолжала сокращать разрыв. В последние минуты матча команда заработала последний тачдаун, еще более сократив разрыв: счет стал 31:30. Команде Небраски достаточно было заработать еще одно очко, чтобы выиграть матч и получить титул чемпиона. Но такая победа не принесла бы команде истинного удовлетворения. Осборн понимал: для того чтобы добиться эффектной победы, команда должна выиграть этот матч.
Игроки Cornhuskers вступили в борьбу за победу, пытаясь добиться перевеса в два очка. Ирвин Фриар получил мяч, но не смог доставить его в очковую зону соперника. Команды Майами и Небраски завершили тот год с равными результатами. Но поскольку команда Майами победила Небраску в финальном матче, именно эта команда заняла первое место в турнирной таблице.
Поставьте себя на место тренера Осборна. Вы смогли бы добиться большего?
Анализ примера
Многие болельщики обвиняли Осборна в том, что он попытался добиться победы, вместо того чтобы довольствоваться ничьей. Но нас интересует не этот вопрос. Осборн был готов пойти на риск, чтобы одержать победу, но он сделал это неправильно. Он добился бы большего, если бы его команда сначала попыталась заработать два очка, доставив мяч в очковую зону. Если бы удалось это сделать, команда могла бы попытаться забить гол и получить еще одно очко; в случае неудачи следовало бы сделать еще одну попытку заработать два очка после тачдауна.
Давайте глубже проанализируем эту ситуацию. Когда команда Осборна проигрывала 14 очков, он уже тогда знал, что ему необходимо заработать два тачдауна и три дополнительных очка. Он решил заработать сначала одно очко, а затем еще два. Если бы обе попытки оказались успешными, порядок, в котором они предпринимались, не имел бы значения. Если бы гол, который обеспечивал одно очко, не был забит, а двухочковая доставка мяча в очковую зону завершилась удачно, то порядок тоже не имел бы значения, поскольку матч закончился бы вничью и команда Небраски получила титул чемпиона. Порядок игры имел бы значение только в том случае, если бы команда Небраски сделала неудачную попытку заработать два очка. Согласно плану Осборна это привело команду Небраски к поражению не только в финальном матче, но и во всем чемпионате. Если бы вместо этого команда попыталась заработать сначала два очка, тогда даже неудачная попытка не обязательно привела бы к поражению. Счет остался бы 31:23. Заработав следующий тачдаун, команда сократила бы разрыв и счет стал бы 31:29. Успешная попытка заработать два очка после тачдауна обеспечила бы команде Небраски ничью, и она заняла бы первое место![65]
Мы слышали и контраргумент: если бы Осборн решил сначала заработать два очка, но эта попытка оказалась неудачной, это означало бы, что его команда играет на ничью. В связи с этим команда рисковала утратить моральный дух, и тогда она вряд ли заработала бы второй тачдаун. С другой стороны, если бы команда разыгрывала два решающих очка в самом конце матча, игроки осознавали бы, что на карту поставлено все, и действовали бы соответственно. Этот аргумент ошибочен по нескольким причинам. Во-первых, если бы команда Небраски попыталась заработать два очка только после второго тачдауна и эта попытка оказалась бы неудачной, она проиграла бы. Но если бы команде не удалось заработать два очка после первого тачдауна, у нее все еще оставался бы шанс на ничью. И хотя этот шанс мог оказаться еще меньше, «что-то» – это больше, чем ничего. Аргумент о динамике игры тоже несостоятелен. Хотя команда Небраски действительно могла бы активизировать наступление в финальной игре чемпионата, можно ожидать, что команда Майами усилила бы при этом свою защиту. Этот матч был важен для обеих команд. Что касается наступательного порыва, то если бы команда Осборна заработала два очка после первого тачдауна, это увеличило бы ее шансы заработать еще один тачдаун. Кроме того, это позволило бы команде закончить матч вничью, забив три гола в ворота соперника.
Один из общих выводов этой истории заключается в следующем: если вам приходится рисковать, в большинстве случаев лучше сделать это как можно скорее. Это очевидно для тех, кто играет в теннис: всем известно, что нужно рисковать на первой подаче, а вторую следует делать более осторожно. В таком случае, если первая попытка закончится неудачей, это не значит, что все потеряно. У вас еще есть время для других действий, которые помогут наверстать упущенное или даже продвинуться вперед. Такой подход (идти на риск как можно раньше) применим во многих областях жизни, будь то выбор карьеры, инвестиции или романтические свидания.
Для того чтобы лучше освоить принцип «смотреть вперед и рассуждать в обратном порядке», ознакомьтесь со следующими учебными примерами, приведенными в главе 14: «Как выбрать самое лучшее место»; «Красное – я выигрываю, черное – ты проигрываешь»; «“Отпугиватель акул” с обратным эффектом»; «Жесткий человек, мягкое предложение»; «Трехсторонняя дуэль»; «Выиграть, не зная как».
Глава 3. Решение дилеммы заключенных
Что общего между следующими ситуациями?
• Две заправочные станции или два супермаркета, расположенных в непосредственной близости друг от друга, время от времени начинают жесткие ценовые войны между собой.
• Во время предвыборной кампании как Демократическая, так и Республиканская партия США часто придерживаются центристской политики, пытаясь привлечь на свою сторону избирателей, не определившихся со своими предпочтениями; при этом они игнорируют основных сторонников, придерживающихся крайних левых и крайних правых взглядов.
• «Разнообразие и продуктивность рыбного промысла в Новой Англии достигли беспрецедентного уровня. Однако сформировавшаяся за прошедшее столетие тенденция чрезмерного промысла привела к вымиранию одного вида рыбы за другим. Атлантический палтус, морской окунь, треска, желтохвостая камбала… пополнили ряды тех видов, которые считаются сейчас вымершими с точки зрения коммерческого промысла»[66].
• В конце известного романа Джозефа Хеллера Catch-22[67] Вторая мировая война уже почти завершилась. Йоссариан не хочет быть среди тех, кто погибнет последним: это уже никак не повлияет на исход войны. Он объясняет это майору Денби, старшему по званию офицеру. Денби спрашивает его: «Но, Йоссариан, представь себе, что получится, если каждый американец станет рассуждать подобным образом?» Йоссариан отвечает ему: «Только круглый дурак рассуждает иначе. Разве я не прав?»[68].
Ответ: все это примеры дилеммы заключенных[69]. Как и во время допроса Дика Хикока и Перри Смита (героев романа «Хладнокровное убийство», о которых шла речь в главе 1), у каждого участника игры есть свои причины сделать то, что повлечет за собой неблагоприятные последствия для обоих, поскольку каждый из них отслеживает только собственные интересы. Если один признается в совершении преступления, другому тоже лучше признаться, чтобы избежать сурового приговора; если один решит воздержаться от признания, другой сможет значительно облегчить свою участь, если признается. В действительности заключенные испытывают в подобной ситуации настолько сильное давление, что у них появляется желание признать свою вину независимо от того, виновны они (как в романе «Хладнокровный убийца») или невиновны, но полиция сфабриковала против них дело (как в фильме «Секреты Лос-Анджелеса»).
То же самое происходит и с ценовыми войнами. Если автозаправочная станция Nexon назначит низкую цену, Lunaco тоже лучше снизить цены, чтобы не потерять клиентов; если Nexon берет высокую цену за свой бензин, Lunaco может привлечь многих покупателей на свою сторону, снизив цену. Но если обе заправочные станции будут продавать бензин по низкой цене, ни одна из них ничего не заработает (хотя клиентам такая цена только на руку).
Если демократы примут предвыборную платформу, ориентированную на сторонников центристской политики, республиканцы рискуют потерять всех этих избирателей, а значит, и проиграть выборы, если будут работать только со своими основными сторонниками из числа борцов за экономические и социальные права; если демократы станут опекать только своих основных сторонников из числа представителей национальных меньшинств и профсоюзов, тогда республиканцы смогут привлечь на свою сторону умеренных избирателей, а значит, победить в выборах со значительным перевесом голосов, придерживаясь более центристской позиции.
Если все рыболовы будут ловить рыбу в умеренных количествах, большой улов одного рыболова не истощит рыбные ресурсы; если же все остальные начнут активно увеличивать промысел, тогда любой отдельный рыболов поступил бы глупо, пытаясь в одиночку охранять рыбные ресурсы[70]. В итоге происходит чрезмерный вылов рыбы и некоторые виды вымирают.
В романе «Уловка-22» именно логика Йоссариана делает таким трудным дальнейшее участие в уже проигранной войне.
Как специалисты по теории игр изобрели и назвали эту игру, которая охватывает так много аспектов экономического, политического и социального взаимодействия? Это произошло еще на начальном этапе истории развития дисциплины. Гарольд Кун, который и сам был одним из пионеров теории игр, рассказал об этом на симпозиуме, который проводился в рамках церемоний вручения Нобелевской премии за 1994 год.
Весной 1950 года Альберт Такер, будучи в отпуске, приехал в Стэнфорд, а поскольку там не хватало кабинетов, его разместили в кабинете кафедры психологии. Однажды кто-то из психологов постучал к нему в дверь и спросил, чем он занимается. Такер ответил: «Я работаю над теорией игр». Психолог спросил, не согласится ли он провести семинар по этой теме. Для этого семинара Такер и придумал дилемму заключенного в качестве примера, иллюстрирующего теорию игр, равновесие Нэша, а также парадоксы, сопутствующие равновесиям, нежелательным с точки зрения общества. Поскольку это был поистине фундаментальный пример, он стал темой десятков научных работ и ряда серьезных книг[71].
Другие ученые рассказывают несколько иную историю. По их мнению, математическая структура игры была описана еще до Такера двумя математиками – Меррилом Фладом и Мелвином Дрешером из Rand Corporation (исследовательский центр, который был в свое время оплотом холодной войны)[72]. Гениальность Такера заключалась в том, что он придумал историю, иллюстрирующую математические выкладки. И это действительно было гениально, поскольку подача идеи может решить ее судьбу: запоминающаяся презентация способствует быстрому распространению идеи среди мыслящих людей, тогда как скучная и сухая – может привести к тому, что идея не получит должного внимания или вообще будет забыта.
Мы проиллюстрируем метод решения этой игры примером из бизнеса. Две конкурирующие компании посылочной торговли – Rainbow’s End и B. B. Lean – специализируются на торговле одеждой. Каждую осень они печатают и рассылают зимние каталоги. Обе компании должны придерживаться тех цен, которые указаны в их каталогах, на протяжении всего зимнего сезона. Период подготовки каталогов гораздо более продолжителен, чем окно для их рассылки, поэтому обе компании должны принимать решения о ценах одновременно, не имея никакой информации о решениях конкурента. В обеих компаниях знают, что их каталоги рассчитаны на общую аудиторию потенциальных покупателей, которые умеют делать покупки с умом и ищут низкие цены.
Как правило, в обоих каталогах публикуется практически идентичный ассортимент товаров. Предположим, один из таких товаров – рубашка из высококачественной ткани шамбре. Такая рубашка обходится каждой компании в 20 долларов[73]. По оценкам обеих компаний, если каждая из них назначит за этот товар цену 80 долларов и продаст 1200 единиц, это обеспечит прибыль в размере (80–20) × 1200 = 72 000 долларов. Кроме того, оказалось, что это наилучшая цена для обеих компаний: если они смогут договориться о том, чтобы назначить одинаковую цену, 80 долларов – это та цена, которая обеспечит обеим максимальную прибыль.
В каждой из компаний подсчитали, что если одна из них снизит цену на 1 доллар, а другая оставит ее неизменной, то компания, снизившая цену, привлечет 100 покупателей: 80 покупателей, перешедших от другой компании, и 20 новых (например, тех, кто решил приобрести рубашку, которую не стали бы покупать по более высокой цене, или покупателей, пожелавших заказать товар по каталогу, вместо того чтобы покупать его в местном торговом центре). Таким образом, у каждой компании есть соблазн назначить более низкую цену, чтобы привлечь больше покупателей. Цель всей этой истории – разобраться в том, чем может обернуться такое решение.
Начнем с предположения о том, что обеим компаниям предстоит выбрать одну из двух цен: 80 и 70 долларов[74]. Если одна компания снизит цену до 70 долларов, а другая оставит цену 80, первая компания привлечет на свою сторону 1000 покупателей, тогда как вторая потеряет 800. Следовательно, компания, снизившая цену, продаст 2200 рубашек, а у другой компании объем продаж сократится до 400 единиц; прибыль составит (70–20) × 2200 = 110 000 долларов у компании, снизившей цену, и (80–20) × 400 = 24 000 – у другой компании.
Что произойдет, если обе компании одновременно снизят цену до 70 долларов? При снижении цены на 1 доллар у компаний останутся имеющиеся покупатели и появятся по 20 новых. Следовательно, если обе компании снизят цену на 10 долларов, каждая из них продаст на 10 × 20 = 200 единиц товара больше предыдущих 1200 единиц. Таким образом, каждая компания продаст по 1400 единиц товара и получит прибыль в размере (70–20) × 1400 = 70 000 долларов.
Представим возможную прибыль обеих конкурирующих компаний в наглядном виде. Мы не можем использовать для этого дерево игры наподобие тех деревьев, которые приведены в главе 2. В данном примере два игрока действуют одновременно. Ни один из них не может сделать очередной ход, опираясь на информацию о том, что сделал другой игрок или какой ответный ход он может предпринять. Вместо этого каждый игрок должен анализировать, о чем в это же время думает другой игрок. Отправная точка для таких «рассуждений о рассуждениях» состоит в том, чтобы отобразить в наглядном виде все последствия каждой комбинации возможных вариантов выбора, который могут одновременно сделать обе компании. Поскольку у каждой из них только одна альтернатива: 80 или 70 долларов, это значит, что существует четыре возможные комбинации. Проще всего отобразить их в виде таблицы, состоящей из столбцов и строк, которую мы будем называть таблицей игры, или таблицей выигрышей. Выбор Rainbow’s End (сокращенно RE) будет отображен в строках этой таблицы, а выбор B. B. Lean (BB) – в столбцах. В каждой из четырех ячеек таблицы, соответствующих каждому выбору RE в строке и BB в столбце, содержатся две цифры, обозначающие прибыль каждой компании от продажи рубашки (в тысячах долларов). Цифра, расположенная в левом нижнем углу ячейки, соответствует тому игроку, для которого выделены строки; цифра в правом верхнем углу ячейки – игроку, для которого выделены столбцы[75]. На языке теории игр эти цифры называются выигрышем[76]. Для того чтобы внести полную ясность в то, какие выигрыши соответствуют каждому из игроков, в представленной таблице соответствующие фрагменты ячеек выделены разными оттенками серого цвета.
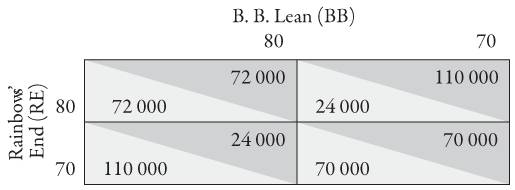
Прежде чем приступить к поиску решения этой игры, мы хотели бы обратить ваше внимание на один ее аспект. Сравните пары выигрышей в четырех ячейках. Лучший результат для RE не всегда означает худший результат для ВВ, и наоборот. В частности, для обеих компаний ситуация в левой верхней ячейке лучше, чем в правой нижней. В конце этой игры не обязательно должен быть победитель и проигравший: это не игра с нулевой суммой. В главе 2 мы уже говорили о том, что инвестиционная игра Чарли Брауна тоже не относится к категории игр с нулевой суммой, как и большинство игр, с которыми мы сталкиваемся в реальной жизни. Во многих играх, таких как дилемма заключенных, главный вопрос заключается в том, как избежать проигрыша или добиться выигрыша обеих сторон.
Проанализируем ход рассуждений менеджера компании RE. «Если ВВ выберет 80 долларов, я могу получить 110 тысяч долларов вместо 72 тысяч, снизив цену до 70 долларов. Если ВВ выберет 70 долларов, мой выигрыш составит 70 тысяч, если я тоже назначу эту цену, и только 24 тысячи долларов, если я оставлю цену 80. Для меня более выгодный вариант (в действительности самый выгодный, поскольку у меня только одна альтернатива) остается неизменным, что бы ни решили в ВВ. Следовательно, мне вообще не нужно думать о том, что думают они; мне просто нужно первым назначить цену 70 долларов».
Если в игре с параллельными ходами есть такое свойство (а именно оптимальный выбор игрока не зависит от выбора других игроков), это существенно упрощает рассуждения игроков, а также анализ, который делают специалисты по теории игр в подобных случаях. Следовательно, наличие такого свойства существенно упрощает решение игры. Специалисты по теории игр обозначают его термином «доминирующая стратегия». Говорят, что у игрока есть доминирующая стратегия, если эта стратегия лучше всех остальных стратегий независимо от того, какую стратегию или сочетание стратегий выберет другой игрок или игроки. Существует простое правило участия в играх с параллельными ходами[77]:
ПРАВИЛО № 2: если у вас есть доминирующая стратегия, примените ее.
Дилемма заключенных – еще более специфичная игра: в ней доминирующая стратегия есть не у одного, а у обоих игроков (или у всех игроков). Менеджер компании ВВ рассуждает точно так же, как менеджер RE; для того чтобы хорошо усвоить эту идею, вы должны самостоятельно проанализировать ход рассуждений менеджера ВВ. Сделав это, вы увидите, что цена 70 долларов – это доминирующая стратегия и для компании ВВ.
Результат применения такой стратегии отображен в правой нижней ячейке таблицы игры: обе компании назначают цену 70 долларов и получают прибыль по 70 тысяч долларов каждая. Необходимо обратить внимание на следующий аспект дилеммы заключенных, который делает ее настолько важной игрой. Когда каждый из игроков применяет свою доминирующую стратегию, оба получают худший результат по сравнению с тем, что они получили бы, если бы доверились друг другу и договорились о том, что каждый выберет другую, доминируемую стратегию. В нашем примере это означало бы, что каждая компания назначит на свой товар цену 80 долларов, для того чтобы получить результат, отображенный в верхней левой ячейке матрицы игры, а именно прибыль в размере 72 тысячи долларов[78].
Для этого было бы недостаточно, чтобы только одна компания назначила на свой товар цену 80 долларов: это повлекло бы за собой очень плохие последствия для этой компании. Так или иначе, обе компании должны назначить высокую цену, чего очень трудно добиться на практике, учитывая существующий у каждой из них соблазн назначить более низкую цену, чем у конкурента. Если обе компании будут преследовать свои эгоистические интересы, они не смогут получить наилучший результат для них обеих. Такой вывод противоречит тому, чему учат нас классические экономические теории, начиная с теории Адама Смита[79].
Это вызывает ряд вопросов, часть которых связана с более общими аспектами теории игр. Что произойдет, если доминирующая стратегия будет только у одного участника игры? Что если ни у одного игрока не окажется доминирующей стратегии? Если оптимальный выбор каждого игрока зависит от того, что в это же время выбирает другой игрок, могут ли они разгадать выбор друг друга и найти решение этой игры? Мы проанализируем ответы на эти вопросы в следующей главе, в которой рассматривается более общий подход к решению игр с параллельными ходами, а именно равновесие Нэша. В данной главе сосредоточимся на решении дилеммы заключенных.
В обобщенном описании дилеммы заключенных две стратегии, имеющиеся в распоряжении каждого игрока, обозначаются так: «сотрудничать» и «предать» (или в некоторых случаях – «обмануть»); мы будем придерживаться именно этих терминов. Предательство – это доминирующая стратегия для каждого игрока; если оба игрока выберут эту стратегию, их выигрыш будет меньше, чем в случае выбора стратегии сотрудничества.
У игроков, столкнувшихся с дилеммой заключенных, есть веские основания для достижения договоренности о совместных действиях, которые позволили бы уйти от ее решения. Например, в Новой Англии рыболовы могут согласиться на ограничение улова ради сохранения рыбных ресурсов на будущее. Проблема состоит только в том, как обеспечить выполнение таких договоренностей в условиях, когда каждая сторона испытывает соблазн обмануть другую (например, выловить рыбы больше, чем позволяет квота). Что говорит теория игр по этому поводу? И что происходит в таких случаях в реальной жизни?
С тех пор как дилемму заключенных сформулировали впервые, прошло более пятидесяти лет. За это время были усовершенствованы теоретические основы этой дилеммы, а также накоплен большой объем данных, полученных как в процессе наблюдений за тем, что происходит в реальной жизни, так и в ходе лабораторных экспериментов. Давайте проанализируем этот материал и посмотрим, какие уроки мы можем из него извлечь.
У стратегии сотрудничества есть обратная сторона: стремление избежать предательства. Игрока можно заинтересовать в том, чтобы он выбрал стратегию сотрудничества вместо доминирующей стратегии предательства, пообещав ему достаточное вознаграждение. Кроме того, его можно удержать от применения стратегии предательства с помощью адекватного наказания.
Метод вознаграждения проблематичен по нескольким причинам. Вознаграждение может носить внутренний характер: один игрок платит другому за выбор стратегии сотрудничества. В иных случаях вознаграждение может быть внешним: третья сторона, заинтересованная в сотрудничестве между двумя игроками, платит им за выбор этой стратегии. Как бы там ни было, вознаграждение нельзя предоставлять игроку, пока он не сделает свой выбор, в противном случае он просто положит его себе в карман, после чего откажется выполнять договоренность. С другой стороны, если вознаграждение просто обещают, игрок может не поверить этому обещанию: когда он выберет стратегию сотрудничества, не исключено, что тот, кто дал это обещание, нарушит его.
Однако, несмотря на все эти трудности, вознаграждение бывает действенным и полезным. Проявив максимум креативности и воображения, игроки могли бы одновременно дать друг другу обещания и сделать их заслуживающими доверия, поместив обещанное вознаграждение на счете условного депонирования, который контролирует третья сторона[80]. В реальной жизни чаще складывается иная ситуация: поскольку игроки взаимодействуют по нескольким направлениям, сотрудничество в одном из них вознаграждается ответной услугой в чем-то другом. Так, самки шимпанзе делятся едой или присматривают за чужими детенышами в обмен на помощь в уходе за шерстью. В некоторых случаях третья сторона может быть заинтересована в обеспечении сотрудничества в игре. Например, ради того чтобы положить конец конфликтам в разных странах мира, Соединенные Штаты Америки и Европейский союз иногда обещают участникам противостояния экономическую помощь в качестве вознаграждения за мирное решение конфликта. Именно таким способом Соединенные Штаты вознаградили Израиль и Египет за сотрудничество в рамках подписания Кэмп-Дэвидских мирных соглашений в 1978 году.
Более распространенный метод решения дилеммы заключенных – наказание. Он имеет прямое действие. В фильме «Секреты Лос-Анджелеса» сержант Эд Эксли обещает Лерою Фонтейну, одному из подозреваемых, что если он согласится стать государственным свидетелем, то получит более мягкий приговор, чем два других подозреваемых, Рэй Коутс и Тайрон Джонс. Но Лерой знает, что, когда он выйдет из тюрьмы, его могут ждать на свободе друзья этих двоих!
Наказание, которое в данном контексте выглядит более естественным, оказывается возможным в связи с тем, что большинство подобных игр представляют собой часть непрерывного взаимодействия. Обман может обеспечить одному игроку краткосрочное преимущество, но навредит его взаимоотношениям с другим игроком и в долгосрочной перспективе обойдется гораздо дороже. Если цена достаточно велика, именно это может удержать игрока от обмана[81].
Наглядный пример такой ситуации предоставляет бейсбол. В Американской бейсбольной лиге питчеры попадают мячом в бэттеров на 11–17 процентов чаще, чем в Национальной бейсбольной лиге. По мнению профессоров Университета Юга в Суони Дага Драйнена и Джона-Чарльза Брэдбери, это обусловлено правилом о назначенном хиттере[82]. В Американской бейсбольной лиге питчеры не бьющие игроки. Следовательно, питчер Американской лиги, который попадает мячом в бэттера, может не бояться ответных действий со стороны питчера команды-соперника. Вероятность того, что мяч попадет в питчера, совсем небольшая, но она повышается в четыре раза, если он попал в кого-то в предыдущей половине иннинга. В таком случае страх получить ответный удар очевиден. Первоклассный питчер Курт Шиллинг объяснил это так: «Вы на самом деле готовы бросить в кого-то мяч, если играете против Рэнди Джонсона?»[83][84].
В ситуации, когда один игрок наказывает другого за обман, действует стратегия «око за око, зуб за зуб». Эта стратегия оказалась настоящим открытием, сделанным в ходе самого известного эксперимента с дилеммой заключенных. В следующем разделе вы узнаете об этом эксперименте и его уроках.
В начале 1980-х годов политолог Мичиганского университета Роберт Аксельрод предложил специалистам по теории игр со всего мира разработать стратегии решения дилеммы заключенных в виде компьютерных программ. Они были распределены по парам, каждая из которых разыгрывала дилемму заключенных 150 раз. На основании набранных очков составили рейтинг программ, принимавших участие в турнире.
Победителем стал профессор математики университета в Торонто Анатолий Рапопорт. Его выигрышная стратегия оказалась одной из самых простых: «око за око, зуб за зуб». Для Роберта Аксельрода этот результат явился большой неожиданностью, поэтому он решил провести еще один турнир, увеличив число участников. Рапопорт и в этот раз подал программу, основанную на той же стратегии, – и снова победил.
Стратегия равноценных ответных действий – один из вариантов правила поведения «поступайте с другими так, как они поступают с вами»[85]. Если говорить более точно, эта стратегия подразумевает сотрудничество на первом этапе, после чего повторяются действия, которые предпринял соперник на предыдущем этапе.
По мнению Роберта Аксельрода, стратегия равноценных ответных действий опирается на четыре принципа, которые должны присутствовать в любой эффективной стратегии для повторяющейся дилеммы заключенных: понятность, доброжелательность, возмездие и прощение. Стратегия равноценных ответных действий очень проста и понятна: сопернику нет необходимости долго размышлять над вашим следующим ходом или просчитывать его. В основе такой стратегии лежит доброжелательность: она никогда не инициирует обман. В этой стратегии есть элемент возмездия: она не оставляет обман безнаказанным. Кроме того, эта стратегия стимулирует прощение: участники игры не держат зла друг на друга слишком долго и готовы возобновить сотрудничество.
Одна из самых впечатляющих характеристик стратегии равноценных ответных действий состоит в том, что она показала лучшие результаты по итогам всего турнира, хотя и не победила (и не могла победить) ни одну из конкурирующих стратегий в прямом противостоянии с ними. В лучшем случае эта стратегия может только сравнять счет с соперником. Следовательно, если бы Аксельрод оценивал каждую игру по принципу «победитель получает все», стратегия равноценных ответных действий имела бы на своем счету только проигрыши и ничьи, а значит, не добилась бы победы по итогам всего турнира[86].
Однако Аксельрод оценивал парные игры между компьютерными программами не по принципу «победитель получает все»: в его турнирах учитывался такой фактор, как готовность к сотрудничеству. Большое преимущество этой стратегии заключается в том, что она сближает соперников. В худшем случае эта стратегия может потерпеть поражение из-за одного предательства, но дальше – только ничья.
Стратегия равноценных ответных действий стала победителем этих соревнований именно потому, что стимулировала сотрудничество, не допуская при этом эксплуатации. Другие стратегии были либо слишком ориентированными на доверие и открытыми для эксплуатации, либо слишком агрессивными и побуждающими игроков выбивать друг друга из игры.
И все-таки мы считаем, что стратегия равноценных ответных действий – ошибочная. Малейший промах или неправильное толкование результатов приводят к полному провалу стратегии. Этот недостаток не был столь очевидным в искусственной среде соревнования между компьютерными программами, поскольку там просто исключались ошибки и неправильное толкование. Однако в случае применения этой стратегии в реальном мире ошибки и заблуждения неизбежны, а результат может оказаться катастрофическим.
Проблема стратегии равноценных ответных действий состоит в том, что обе стороны противостояния повторяют ошибки и заблуждения друг друга. Одна сторона наказывает другую за предательство, и это вызывает цепную реакцию. Соперник отвечает на наказание ответным ударом, который влечет за собой очередное наказание. В таком противостоянии может и не наступить момент, когда одна из сторон приняла бы наказание без ответного удара.
Предположим, Флад и Дрешер разыгрывают стратегию равноценных ответных действий. Поначалу ни один из них не идет на предательство, поэтому какое-то время все складывается хорошо. Затем, скажем, в 11-м раунде игры Флад по ошибке выбирает стратегию «предать» или останавливается на стратегии «сотрудничать», но Дрешер по ошибке считает, что Флад выбрал предательство. В любом случае Дрешер выберет в 12-м раунде ход «предать», но Флад выберет стратегию «сотрудничать», поскольку Дрешер выбрал сотрудничество в 11-м раунде. В 13-м раунде они поменяются ролями. Ситуация, когда один из игроков выберет сотрудничество, а другой – предательство, будет повторяться снова и снова до тех пор, пока очередная ошибка или заблуждение не восстановят сотрудничество между соперниками или не заставят каждого из них выбрать предательство.
Такие циклы или ответные удары часто наблюдаются во время реальных конфликтов между израильтянами и арабами на Ближнем Востоке, или между католиками и протестантами в Северной Ирландии, или между индусами и мусульманами в Индии. На границе между штатами Западная Вирджиния и Кентукки шла памятная вражда между Хэтфилдами и Маккоями. В художественной литературе тоже можно найти яркие примеры того, как такие действия могут привести к непрекращающемуся циклу ответных ударов, как в случае вражды между Грэнджерфордами и Шепердсонами в романе Марка Твена.
Да из-за чего же вышла ссора, Бак? Из-за земли?
– Я не знаю. Может быть.
– Ну а кто же первый стрелял? Грэнджерфорд или Шепердсон?
– Господи, ну почем я знаю! Ведь это так давно было.
– И никто не знает?
– Нет, папа, я думаю, знает, и еще кое-кто из стариков знает; они только не знают, из-за чего в самый первый раз началась ссора[87].
Стратегия равноценных ответных действий не предполагает возможности остановить этот порочный круг. Она слишком ориентирована на возмездие и недостаточно стимулирует прощение. В следующих версиях соревнований, которые устраивал Роберт Аксельрод, предусматривалась возможность ошибок и заблуждений; в итоге другие, более бескорыстные, стратегии показали свое превосходство над стратегией равноценных ответных действий[88].
Здесь мы можем научиться чему-то даже у обезьян. В ходе одного эксперимента с хохлатыми тамаринами одной из обезьян давали возможность потянуть рычаг, чтобы другая могла достать пищу. Однако для того, чтобы потянуть рычаг, следовало приложить усилие. Теоретически каждой обезьяне было бы выгоднее ничего не делать, пока партнер тянет рычаг. Но тамарины научились сотрудничать, чтобы избежать возмездия. Их сотрудничество сохранялось до тех пор, пока одна из обезьян два раза подряд не совершила предательство. Эта стратегия представляет собой разновидность стратегии «зуб за зуб», а именно – «два зуба за зуб»[89].
Дилемма заключенных стала объектом тысяч экспериментов с участием разного числа игроков, с повторениями и с другой трактовкой условий игры. Вот некоторые важные выводы, сделанные в ходе этих экспериментов[90].
Первый и самый важный вывод состоит в том, что игроки выбирают стратегию сотрудничества достаточно часто, даже если два игрока попадают в одну пару только один раз. В среднем почти половина игроков отдают предпочтение сотрудничеству. Самое впечатляющее доказательство этого факта было получено в ходе проведения телевикторины Friend or Foe («Друг или враг») на канале Game Show Network. Командам из двух человек задавали достаточно простые вопросы. Деньги, полученные участниками за правильные ответы, уходили в «трастовый фонд»; за 105 эпизодов в таком фонде накапливалось от 200 до 16 400 долларов. Для того чтобы разделить эти деньги, двум участникам предстояло решить следующую дилемму.
Каждый игрок должен был написать на листе бумаги слово «друг» или «враг». Если оба написали «друг», деньги делились поровну. Если один игрок написал «враг», а другой – «друг», весь выигрыш получал тот, кто написал «враг». Но если оба игрока написали «враг», ни один из них не получал ничего. Что бы ни сделала другая сторона, каждый игрок мог получить минимум столько же, сколько его соперник (или даже больше), если бы он написал «враг», а не «друг». Тем не менее почти половина участников шоу писали слово «друг». Даже когда призовой фонд увеличивался, вероятность того, что игроки выберут сотрудничество, оставалась прежней. Люди были в равной степени готовы сотрудничать, когда на кону стояло три и пять тысяч долларов. К таким же выводам пришли в ходе исследований Феликс Оберхольцер-Джи, Джоэль Вальдфогель, Мэтью Уайт и Джон Лист[91].
Если вы сомневаетесь, можно ли считать телевизионное шоу научным исследованием, обратите внимание на следующий факт: участникам телевикторины выплатили более 700 тысяч долларов. У этого эксперимента с дилеммой заключенных оказалось самое лучшее финансирование за всю историю экспериментов такого рода. Кроме того, по результатам викторины было сделано много важных выводов. Оказалось, что женщины в большей степени готовы идти на сотрудничество, чем мужчины: 53,7 процента (в первом сезоне – 47,5 процента). В первом сезоне участники шоу не имели возможности увидеть результаты других состязаний перед тем, как принимать решение. А вот во втором сезоне были оглашены результаты первых 40 эпизодов, что позволяло увидеть закономерность. Участники шоу учились на опыте своих предшественников. Если команда состояла из двух женщин, коэффициент сотрудничества повышался до 55 процентов, а когда в состав команды входили одна женщина и один мужчина, этот коэффициент падал до 34,2 процента. У мужчин в этом случае коэффициент сотрудничества тоже снижался до 42,3 процента. В целом готовность участников шоу сотрудничать уменьшалась на десять пунктов.
Когда группу участников эксперимента несколько раз разбивают по парам, каждый раз формируя новые пары, число людей, которые выбирают сотрудничество, со временем сокращается. Тем не менее это число не сводится до нуля; вместо этого формируется небольшая группа участников эксперимента, неизменно отдающих предпочтение сотрудничеству.
Если одна и та же пара играет в базовую игру с дилеммой заключенных много раз подряд, в большинстве случаев образуется весьма значительная последовательность взаимного сотрудничества; это продолжается до тех пор, пока один из игроков уже в самом конце серии игр не выберет стратегию предательства. Именно это произошло в ходе первого эксперимента с дилеммой заключенных. Как только Меррил Флад и Мелвин Дрешер придумали эту игру, они предложили двум своим коллегам сыграть в нее 100 раз[92]. В 60 раундах игры оба участника выбрали стратегию сотрудничества. Длинный период взаимного сотрудничества продолжался с 83-го по 98-й раунд, пока в 99-м раунде один из игроков не выбрал стратегию предательства.
Если следовать строгой логике теории игр, то в действительности этого не должно было произойти. Если игра повторяется ровно 100 раз, она представляет собой серию игр с одновременными ходами, а значит, мы можем применить к ней логику обратных рассуждений. Определите, что произойдет в сотом раунде. Это последний раунд игры, поэтому предательство не может быть наказано в следующих раундах. В таком случае, согласно принципу доминирующей стратегии, оба игрока должны выбрать в последнем раунде стратегию предательства. Но как только принимается такое предположение, последним становится, по сути, 99-й раунд. Хотя игрокам предстоит еще один раунд, выбор стратегии предательства в 99-м раунде не может быть наказан в 100-м раунде, поскольку сделанный в этом раунде выбор предопределен. Следовательно, логика доминирующей стратегии применима и к 99-му раунду. Эти рассуждения можно продолжить до первого раунда. Однако в реальной игре, будь то в лаборатории или в реальном мире, игроки склонны игнорировать эту логику и пытаются извлечь выгоду из взаимного сотрудничества. Поведение, которое на первый взгляд может показаться иррациональным (отказ от доминирующей стратегии), оказывается правильным выбором при условии, что другие игроки ведут себя столь же иррационально.
Специалисты по теории игр предлагают следующее объяснение этого феномена. В этом мире есть люди, которые всегда поступают с другими так, как поступают с ними; такие люди готовы сотрудничать до тех пор, пока другие делают то же самое. Предположим, вы не принадлежите к числу этих достаточно милых людей. Если бы в игре с конечным числом повторений вы вели себя так, как того требует ваш тип личности, вы начали бы с обмана. Это раскрыло бы ваш характер другому игроку. Для того чтобы скрыть правду (хотя бы на какое-то время), вам придется вести себя достойно. Зачем вам делать это? Предположим, вы начнете игру, поступив порядочно. Если другой игрок не относится к тем, кто всегда платит той же монетой, он подумает, что вы, возможно, принадлежите к числу тех немногих людей, которых можно назвать порядочными. Временное сотрудничество может принести определенную выгоду, поэтому другой игрок, желая получить эту выгоду, попытается ответить на вашу порядочность тем же. Это пойдет на пользу и вам. Разумеется, при этом вы (так же, как и другой игрок) планируете перейти к стратегии предательства к концу игры. Тем не менее на начальном этапе игры вы оба можете поддерживать взаимовыгодное сотрудничество. Хотя каждый игрок ждет момента, когда удастся воспользоваться порядочностью другого, этот взаимный обман приносит пользу им обоим.
В ходе некоторых экспериментов вместо распределения испытуемых по парам и проведения серии игр с дилеммой заключенных организуется большая игра с участием всей группы. Мы хотим привести здесь особенно интересный и поучительный пример. Профессор Реймонд Батталио из Техасского сельскохозяйственно-машиностроительного университета организовал следующую игру с участием 27 студентов[93]. Все студенты, якобы владельцы гипотетических компаний, должны были решить (одновременно и независимо друг от друга, написав свое решение на листике бумаги), какой объем продукции будет выпускать их компании: 1, который поможет сохранить совокупное предложение на низком уровне, а цены – на высоком, или 2, который позволит получить дополнительный доход за счет других. В зависимости от числа студентов, которые выберут объем продукции 1, деньги будут выплачены им по следующей схеме:

На графике эта схема представлена в наглядном виде.
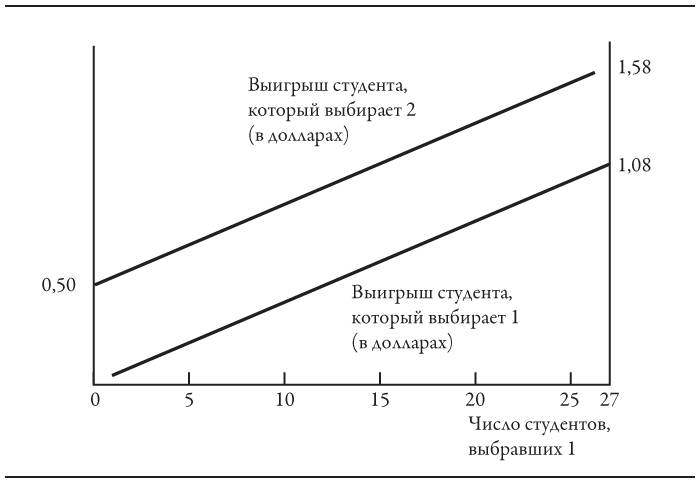
Игра построена таким образом, чтобы студенты, выбравшие 2 («предать»), всегда получали на 50 центов больше, чем студенты, выбравшие 1 («сотрудничать»), но чем больше студентов выбирают 2, тем меньше их совокупный выигрыш. Предположим, все 27 студентов начинают с выбора 1; в таком случае каждый из них получит по 1,08 доллара. А теперь представьте себе, что один из них переключается на вариант 2. В игре остается 26 студентов, выбравших 1; каждый из них получит по 1,04 доллара (на 4 цента меньше, чем по первоначальному плану), но студент, изменивший стратегию, получит 1,54 доллара (на 46 центов больше). Такое распределение выигрыша не зависит от первоначального числа студентов, намеревающихся выбрать 1, а не 2. В данном случае вариант 2 – это доминирующая стратегия. Каждый студент, который переключается со стратегии 1 на стратегию 2, увеличивает свой выигрыш на 46 центов, но в то же время сокращает выигрыш каждого из оставшихся 26 участников игры на 4 цента. Когда все участники игры начнут действовать эгоистично, пытаясь получить максимальный выигрыш, каждый из них получит по 50 центов. Если бы они могли успешно объединить свои усилия и выбрать такой образ действий, который свел бы их общий выигрыш к минимуму, каждый из них получил бы по 1,08 доллара. А как вы сыграли бы в эту игру?
Когда эта игра проводилась на практике (один раз без обсуждения в группе, другой раз с обсуждением, для того чтобы выработать согласованные действия), число студентов, которые были готовы сотрудничать и выбрали вариант 1, колебалось от 3 до 14. В последней игре, в которой студенты объединили свои усилия, их было 4. Совокупный выигрыш составил 15,82 доллара, что было на 13,34 доллара меньше, чем в том раунде игры, в котором студентам удалось договориться. «Я больше никогда в жизни не стану никому доверять!» – недовольно пробормотал студент, который больше всех выступал за согласованные действия. Но каким был его выбор? «Ну, я выбрал 2», – сказал он. Йоссариан понял бы его.
В современных экспериментах с играми в дилемму заключенных с несколькими участниками используется вариант, получивший название «игра со взносами в общий фонд». Каждому игроку предоставляется некая начальная сумма, скажем, 10 долларов. После этого он решает, какую часть этой суммы оставит себе и какую отдаст в общий фонд. Затем экспериментатор удваивает сумму, накопившуюся в общем фонде, и делит ее поровну между всеми участниками игры (как теми, которые сделали взнос в общий фонд, так и теми, которые оставили всю сумму себе).
Предположим, в группу входят четыре игрока: А, Б, В и Г. Независимо от действий других игроков, если А решит внести 1 доллар в общий фонд, после удваивания сумма в общем фонде увеличится на 2 доллара. Но 1,5 доллара достанется при этом игрокам Б, В и Г; сам игрок А получит всего 50 центов. Следовательно, игрок А потеряет еще больше денег, если увеличит взнос в общий фонд; напротив, он будет в выигрыше, если сократит размер этого взноса. И такая ситуация складывается независимо от того, какой взнос в общий фонд делают другие игроки (и делают ли они его вообще). Иными словами, для игрока А доминирующая стратегия состоит в том, чтобы не вносить в общий фонд ничего. То же самое верно и для игроков Б, В и Г. Согласно этой логике, каждый участник игры должен рассчитывать на то, что он сможет стать «безбилетником» – получить выгоду от действий других игроков, не делая никакого взноса в общий фонд. Если все четыре игрока будут придерживаться своей доминирующей стратегии, общий фонд останется пустым, а каждый участник игры просто сохранит свою первоначальную сумму 10 долларов. Если каждый попытается проехаться «зайцем», автобус так и не сдвинется с места. С другой стороны, если бы каждый игрок внес в общий фонд всю имеющуюся у него сумму – 10 долларов, после удваивания в фонде оказалось бы 80 долларов, а доля каждого игрока составила бы 20 долларов. Но у каждого из них свои мотивы в такой игре. В этом и состоит их дилемма.
Игра со взносами в общий фонд – это не только объект лабораторных экспериментов или теоретических изысканий; она разыгрывается в реальном мире в тех случаях социального взаимодействия, когда некое общее благо можно создать только благодаря добровольному вкладу членов группы, но доступ к нему нельзя запретить тем членам группы, которые не внесли свой вклад в общее дело. Такая ситуация складывается, например, в случаях борьбы с наводнениями или рационального использования природных ресурсов: дамбы или плотины невозможно построить так, чтобы паводковые воды затопляли поля только тех обитателей деревни, которые не принимали участия в строительстве противопаводковых сооружений. Что касается рационального использования газа и рыбных ресурсов, на практике просто невозможно в будущем не допускать к этим ресурсам тех, кто сверх меры потреблял их в прошлом. Именно это и создает дилемму в игре с участием нескольких игроков: каждый игрок испытывает соблазн уклониться от работы или не делать взнос в общий фонд, рассчитывая на получение выгоды от вклада других участников группы. Когда так рассуждают все игроки, результат совместных действий оказывается совсем небольшим или вообще отсутствует, что негативно сказывается на всей группе. Эта ситуация встречается настолько часто, что во всех областях социальной теории и социальной политики возникла потребность в глубоком понимании методов решения данной дилеммы.
Возможно, самый интересный вариант этой игры – когда игрокам предоставляется возможность наказывать тех, кто нарушает принятое по умолчанию социальное соглашение о сотрудничестве. Однако связанные с этим издержки должны взять на себя все участники. После того как игра со взносами в общий фонд завершена, информация о взносе каждого игрока доводится до сведения всех остальных. Затем проводится второй этап игры, в ходе которого каждый игрок может предпринять действия, направленные на сокращение выигрыша других игроков, но это обойдется ему в какую-то сумму (как правило, около 33 центов) на каждый доллар того сокращения, которое он выбрал. Иными словами, если игрок А решает сократить выигрыш игрока Б на три доллара, выигрыш игрока А сократится на один доллар. Деньги, высвободившиеся в результате такого сокращения, не передаются никому другому, а возвращаются в фонд экспериментатора.
Результаты этого эксперимента говорят о том, что его участники склонны наказывать нарушителей социальных договоренностей (так называемых социальных обманщиков), взыскивая с них значительную сумму денег. Перспектива наказания существенно увеличивает размер взносов в общий фонд на первом этапе игры. По всей вероятности, наказание – это эффективный способ достижения сотрудничества, который приносит пользу всей группе. Однако тот факт, что люди действительно прибегают к этому методу, кажется неожиданным только на первый взгляд. Наказание других за свой счет – это уже вклад в общее благо. Это доминируемая стратегия, но если она стимулирует обманщика вести себя лучше в будущем, это приносит пользу всей группе, а наказавший получает только малую долю от этой выгоды. Следовательно, наказание должно быть следствием чего-то большего, чем сугубо эгоистический расчет. И это действительно так. В ходе ряда экспериментов проводилась позитронно-эмиссионная томография мозга игроков[94]. Оказалось, что применение наказания активизирует дорсальный стриатум – участок головного мозга, который отвечает за удовольствие и удовлетворенность. Иными словами, люди действительно получают психологическую выгоду или удовольствие, наказывая нарушителей коллективных договоренностей. По всей вероятности, этот инстинкт имеет глубокие биологические корни и прошел процесс отбора потому, что обеспечивает эволюционное преимущество[95].
На основании всех этих примеров и экспериментов можно выделить ряд предпосылок и стратегий успешного сотрудничества. Далее представлено систематизированное описание этих концепций, а также приведены примеры их применения в реальной жизни.
Успешная система наказания должна удовлетворять ряду требований.
Определение обмана. Нельзя наказывать кого-то за обман, не установив сам факт обмана. Если обман обнаруживается быстро и безошибочно, наказание может быть незамедлительным и адекватным. Это позволяет снизить выигрыш от обмана и увеличить связанные с ним издержки, а значит, повышает вероятность успешного сотрудничества. Так, авиакомпании постоянно отслеживают цены конкурентов; если бы в American Airlines захотели снизить плату за перелет из Нью-Йорка в Чикаго, в United Airlines могли бы ответить тем же не более чем через пять минут. Однако компании, желающие снизить свои цены, могут сделать это посредством тайных сделок с клиентами или скрыть снижение цен в сложных сделках со множеством разных условий, таких как сроки доставки, качество продукции, гарантийные обязательства и так далее. В самом крайнем случае каждая компания может отслеживать данные только о своих продажах и прибылях, которые зависят и от ряда случайных факторов, в том числе действий других компаний. Например, объем продаж компании бывает обусловлен колебаниями спроса, а не только тайным снижением цен конкурирующей компанией. В таком случае процесс обнаружения обмана и наказания за него протекает не только медленно, но и не совсем правильно, что усиливает искушение обмануть снова.
В заключение следует отметить, что, когда в одном сегменте рынка работают две-три компании одновременно, они должны установить не только сам факт обмана, но и кем совершен этот обман. В противном случае наказание носит не адресный, а расплывчатый характер и может развязать ценовую войну, которая повредит всем без исключения.
Характер наказания. Далее необходимо решить, каким именно должно быть наказание. Иногда в распоряжении игроков есть возможность наказать других участников игры буквально сразу же после обнаружения обмана даже в процессе однократного взаимодействия. Как мы уже отметили при обсуждении дилеммы, возникшей перед героями фильма «Секреты Лос-Анджелеса», друзья Рэя Коутса и Тайрона Джонса дождутся, когда Лерой Фонтейн выйдет из тюрьмы, и накажут его за то, что он стал государственным свидетелем ради более мягкого приговора. В эксперименте с участием студентов Техасского университета, когда они могли определить, кто нарушил договоренность о выборе варианта 1, у них была возможность применить к обманщикам социальные санкции, такие как остракизм. В этом случае мало кто из студентов пошел на такой риск ради 50 центов.
Другие виды наказания возникают благодаря самой структуре игры. Как правило, это происходит в повторяющихся играх, когда выигрыш от обмана в одном раунде игры приводит к проигрышу в будущих раундах. Достаточно ли этого, чтобы удержать от обмана того игрока, который допускает такую возможность, зависит от размера выигрыша и проигрыша, а также от важности будущих событий по отношению к настоящим. Далее мы проанализируем этот аспект.
Понятность. Потенциальный обманщик должен понимать границы приемлемого поведения, а также последствия обмана. Если эти аспекты игры слишком сложны, игрок может допустить обман по ошибке или потому, что не сумел просчитать свои ходы и играл интуитивно. Возьмем в качестве иллюстрации такой пример. Предположим, компании Rainbow’s End и B. B. Lean постоянно играют в игру с установлением цен и в RE приходят к выводу, что если средняя дисконтированная прибыль RE за последние 17 месяцев окажется на 10 процентов ниже реальной средней нормы прибыли на промышленный капитал за тот же период, это будет означать, что в ВВ пошли на обман. ВВ ничего не известно об этом правиле напрямую; специалистам этой компании придется делать косвенные выводы о том, какое правило применяют в RE, наблюдая за действиями этой компании. Однако сформулированное здесь правило может оказаться слишком сложным для ВВ, так что это не такой уж хороший способ удержать ВВ от обмана. А вот стратегия равноценных ответных действий совершенно понятна: если ВВ пойдет на обман, RE сразу же ответит на это снижением цен.
Неизбежность. Игроки должны быть уверены в том, что предательство будет наказано, а сотрудничество – вознаграждено. Отсутствие такой уверенности – основная проблема некоторых международных соглашений, таких как соглашения о снятии торговых ограничений, которые заключает Всемирная торговая организация (ВТО). Когда одна страна жалуется на то, что другая нарушила соглашение, ВТО инициирует административный процесс, который тянется несколько месяцев или даже лет, а наказание зависит скорее не от фактических обстоятельств дела, а от требований международной политики и дипломатии. Вряд ли такие меры по обеспечению выполнения соглашений можно назвать эффективными.
Размер. Насколько суровым должно быть наказание? По всей видимости, здесь не следует устанавливать никаких ограничений. Если наказание достаточно суровое, чтобы удержать игроков от обмана, просто не будет необходимости его применять. Следовательно, можно ввести достаточно серьезное наказание, которое действительно станет сдерживающим фактором. Например, ВТО предусмотрит в своем уставе пункт о применении ядерного оружия против страны, которая помешает попыткам этой организации удерживать протекционистские тарифы на низком уровне, установленном по общему согласию стран – членов ВТО. Вы наверняка содрогнулись от ужаса – отчасти потому, что допускаете возможность ошибки, которая повлечет за собой такие последствия. Если ошибки действительно возможны (как это и бывает в реальной жизни), наказание необходимо устанавливать на минимальном уровне, обеспечивающем успешное сдерживание при любых обстоятельствах. В самых крайних случаях бывает целесообразно даже простить отдельные случаи нарушения договоренностей. Компании, которая борется за выживание, можно позволить немного снизить цены, не опасаясь ответных мер со стороны конкурентов.
Повторяемость. Вернемся к ценовой игре между компаниями Rainbow’s End и B. B. Lean. Предположим, им из года в год удается поддерживать цены на оптимальном для обеих компаний уровне – 80 долларов. Но вот менеджеры RE рассматривают возможность снизить цену до 70 долларов. По их подсчетам, это принесло бы RE дополнительную прибыль в размере 110 000 – 72 000 = 38 000 долларов. Однако это может разрушить доверие между компаниями. В RE должны понимать, что в будущем ВВ тоже решат снизить цену до 70 долларов и обе компании смогут зарабатывать только по 70 000 долларов в год. Если бы в RE придерживались первоначальной договоренности, обе компании зарабатывали бы по 72 000 долларов. Следовательно, если RE снизит цену, это обойдется ей в 72 000 – 70 000 = 2000 долларов за каждый будущий год. Стоит ли разовый выигрыш в размере 38 тысяч долларов того, чтобы все последующие годы терять по две тысячи долларов в год?
Процентная ставка – один из главных факторов, от которых зависит равновесие между настоящим и будущим. Предположим, процентная ставка составляет 10 процентов в год. Компания RE может положить на счет свои 38 тысяч долларов и зарабатывать по 3800 долларов в год. Это полностью покрывает убытки компании в размере двух тысяч долларов за каждый очередной год. Следовательно, RE выгодно пойти на обман конкурента. Но если процентная ставка составляет только пять процентов в год, тогда сумма 38 тысяч долларов принесет компании всего 1900 долларов в каждом следующем году, а это меньше убытков в размере двух тысяч долларов, которые понесет RE вследствие нарушения договоренности, поэтому компания решает не снижать цену. Процентная ставка, при которой будет достигнуто равновесие, равна 2/38 = 0,0526, или 5,26 процента в год.
Основная идея всех этих рассуждений выглядит следующим образом: если процентная ставка достаточно низкая, будущее имеет относительно более высокую ценность. Например, если процентная ставка – 100 процентов, будущее имеет низкую ценность по отношению к настоящему: год спустя один доллар – это всего 50 центов сейчас, поскольку через год вы можете превратить эти 50 центов в один доллар, заработав еще 50 центов на процентах за этот год. Но если процентная ставка равна нулю, то год спустя один доллар будет стоить столько же, сколько сейчас[96].
В нашем примере более близкая к реальности процентная ставка – пять процентов, поэтому соблазн каждой компании снизить цену на 10 долларов ниже оптимальной для них обеих цены 80 долларов хорошо сбалансирован, а согласование действий в повторяющейся игре не всегда бывает возможным. В главе 4 мы увидим, насколько может упасть цена, если над участниками игры не нависает тень будущего, а соблазн обмануть соперника становится непреодолимым.
Еще один важный фактор, который необходимо учитывать в играх такого рода, – это вероятность дальнейшего взаимодействия. Если рубашка – это предмет преходящей моды, который может и не продаваться на протяжении всего следующего года, перспектива будущих убытков не подавит соблазн обмануть конкурента в текущем году.
Однако Rainbow’s End и B. B. Lean продают много других товаров, кроме этой рубашки. Не приведет ли попытка снизить цену на рубашку к ответным действиям конкурента по всем остальным товарам? И разве перспектива такого серьезного ответного хода недостаточна для того, чтобы удержаться от стратегии предательства? Увы, не так уж просто достичь устойчивого сотрудничества между компаниями, опираясь на практическую ценность их взаимодействия по всему ассортименту товаров. Перспектива ответных действий по всем товарам неразрывно связана с перспективой получить немедленный выигрыш благодаря серии обманных действий по всем этим направлениям, а не только по одному. Если бы таблицы выигрышей по всем товарам были идентичными, прибыли и убытки увеличились бы ровно во столько раз, сколько товаров есть у каждой компании, и это не повлияло бы на общий итог. Следовательно, успешное наказание в дилемме со множеством товаров носит не столь явный характер и зависит скорее от различий между самими товарами.
Третий важный момент, имеющий отношение к данной теме, – это прогнозируемое изменение объема бизнеса в течение продолжительного периода. У такого изменения может быть два аспекта: устойчивый рост или падение и колебания. Если бизнес будет расти, компании, которая рассматривает возможность предательства в текущий момент, необходимо учитывать, что в будущем она рискует понести более серьезные убытки из-за потери сотрудничества. Напротив, если объем бизнеса сокращается, компании испытывают более сильное искушение пойти на предательство и получить максимум возможного сейчас, зная, что их будущее под угрозой. Что касается колебаний, компании более склонны обманывать конкурентов, когда наступает временный подъем: в таком случае обман обеспечит им больше прибыли уже сейчас, тогда как негативное влияние потери сотрудничества ударит по ним лишь в будущем, когда объем бизнеса окажется на среднем уровне. Следовательно, можно предположить, что ценовые войны должны возникать в период высокого спроса. Но так бывает не всегда. Если период низкого спроса наступает вследствие общего падения экономики, у потребителей сокращаются доходы и они делают покупки более осторожно: их лояльность по отношению к той или иной компании может измениться, а реакция на различия в ценах – ускориться. При таком развитии событий компания, снижающая цены, вправе рассчитывать на то, что ей удастся привлечь на свою сторону больше клиентов, переманив их от конкурента, а значит, и получить за счет такого обмана больше прибыли в ближайшем будущем.
И последнее: большую роль в достижении сотрудничества играет состав группы игроков. Если он стабилен и предполагается, что он останется таким и в будущем, это способствует поддержанию сотрудничества. Новые игроки, не заинтересованные в сотрудничестве или у которых нет истории участия в данном соглашении о сотрудничестве, с меньшей вероятностью будут его придерживаться. Если существующая группа игроков ожидает, что в ближайшем будущем появятся новые игроки, которые нарушат принятую по умолчанию договоренность о сотрудничестве, это усиливает их готовность обмануть конкурентов и воспользоваться хотя бы какими-то дополнительными выгодами уже сейчас.
Иногда можно услышать утверждения, будто участники игры с дилеммой заключенных выбирают сотрудничество потому, что принимают решение не только ради себя, но и ради соперника. На самом деле это заблуждение, но люди поступают подобным образом, будто это действительно так и есть.
Каждый участник игры хочет, чтобы другой игрок выбрал сотрудничество, и решает для себя, что его соперник придерживается такой же логики принятия решений, что и он. По мнению такого участника игры, другой игрок должен сделать такие же логические выводы, какие сделал он сам. Следовательно, если игрок выбирает сотрудничество, он считает, что другой игрок сделает то же самое; если же он выбирает стратегию предательства, он приходит к выводу, что это заставит другого игрока тоже предать. Это напоминает категорический императив Канта: «Поступай лишь согласно той максиме, которую ты желал бы видеть всеобщим законом».
Разумеется, это очень далеко от истины. Действия одного игрока не оказывают никакого влияния на другого игрока. И все же людям кажется, что их действия, даже если они незаметны, могут повлиять на выбор других участников игры.
Сила такого образа мыслей была показана в ходе эксперимента с участием студентов Принстонского университета, который провели Эльдар Шафир и Амос Тверски[97]. Исследователи предложили студентам сыграть в игру с дилеммой заключенных. Однако в отличие от обычной схемы проведения такой игры в некоторых случаях они сообщали одному игроку, что сделал другой. Когда студентам говорили, что другой игрок выбрал стратегию предательства, только три процента отвечали на это сотрудничеством. Когда игрокам говорили, что их соперник выбрал сотрудничество, это приводило к увеличению доли игроков, выбравших сотрудничество, до 16 процентов. Следовательно, подавляющее большинство студентов все же предпочитали действовать исходя из собственных интересов. Тем не менее многие из них были готовы ответить сотрудничеством на сотрудничество, даже если ради этого им приходилось чем-то пожертвовать.
Как вы думаете, что происходило, когда студентам не сообщали о выборе других игроков? Осталась ли доля участников игры, готовых пойти на сотрудничество, в пределах от 3 до 16 процентов? Нет, она увеличилась до 37 процентов. На первый взгляд может показаться, что это лишено всякого смысла. Если вы не выбрали сотрудничество, ни тогда, когда знали, что другая сторона выбрала стратегию предательства, ни тогда, когда знали, что другая сторона выбрала стратегию сотрудничества, с какой стати вам выбирать сотрудничество, если вы не знаете, что сделала другая сторона?
Эльдар Шафир и Амос Тверски называют это «квазимагическим мышлением» – верой в то, что, предпринимая какие-либо действия, вы можете повлиять на действия другой стороны. Когда людям сообщают, что сделала другая сторона, они осознают, что не могут этого изменить. Но если они не знают об этом, им кажется, что их действия могут иметь какое-то влияние или что другая сторона так или иначе применит ту же цепочку рассуждений и придет к тем же выводам, что и они. Поскольку вариант «сотрудничать, сотрудничать» более предпочтителен по сравнению с вариантом «предать, предать», они выбирают сотрудничество.
Следует отметить, что такая логика совершенно нелогична. Ваши мысли и действия не имеют никакого влияния на мысли и действия других людей. Им приходится принимать решения, не зная, что вы думаете и какие действия предпринимаете. Тем не менее факт остается фактом: если бы членам общества было свойственно такое квазимагическое мышление, они не становились бы жертвами дилеммы заключенных и получали более весомый выигрыш от взаимодействия друг с другом. Может ли человеческое общество намеренно прививать своим членам такое мышление ради этой великой цели?
Вооружившись в предыдущих разделах таким набором инструментов, как экспериментальные данные и теоретические концепции, выйдем из лаборатории в реальный мир, проанализируем некоторые примеры дилеммы заключенных и попытаемся найти ее решение.
Начнем с дилеммы, которая возникает у конкурирующих компаний в той или иной отрасли. Их общим интересам больше всего отвечают монополизация или картелизация этой отрасли и поддержание цен на высоком уровне. Однако каждая из этих компаний сумеет добиться большего для себя, если нарушит соглашение и пойдет на снижение цен, для того чтобы отнять бизнес у конкурентов. Что же могут сделать эти компании в такой ситуации? Некоторые факторы, способствующие успешному сговору между компаниями (такие как повышение спроса или отсутствие нового игрока, способного нарушить сложившуюся ситуацию), останутся – как минимум частично – вне их контроля. Однако компании могут создать условия для успешного обнаружения обмана и разработать эффективную стратегию наказания.
Достичь такого сговора легче, если компании регулярно проводят встречи своих представителей и обмениваются информацией. В таком случае в процессе переговоров они постараются найти компромисс по поводу того, какие методы работы считать приемлемыми и что представляет собой обман. Процесс переговоров и его итоги способствуют внесению ясности в сложившуюся ситуацию. Если происходит событие, которое можно расценивать как обман (при отсутствии доказательств противного), еще одна встреча позволит понять, что это на самом деле – невинная случайная ошибка или сознательный обман. Следовательно, такой подход способен предотвратить ненужные наказания. Кроме того, встреча помогает выработать адекватные действия в случае, если наказание все-таки понадобится.
Проблема состоит в том, что успешное решение такой дилеммы в рамках группы участников отрасли наносит вред интересам общества. Потребители вынуждены платить завышенную цену, а компании не поставляют часть своих запасов на рынок, чтобы поддерживать цены на высоком уровне. Как сказал Адам Смит, «люди одной профессии редко собираются вместе даже для развлечения, но их встречи заканчиваются заговором против общества или планом увеличить расценки»[98]. Правительства, которые стремятся защитить интересы общества, вмешиваются в подобные ситуации и вводят в действие антимонопольные законы, запрещающие компаниям вступать в сговор[99]. В США антимонопольный закон Шермана запрещает любой сговор, направленный на ограничение торговли и монополизацию отрасли. Ценовой сговор или сговор в целях закрепления доли на рынке – самые распространенные примеры такого сговора. Верховный суд США не только вынес запрет на официальные соглашения подобного рода, но и постановил, что любая явная или негласная договоренность между компаниями, которая приводит к фиксации цен, – это нарушение закона Шермана независимо от первоначальных намерений. Нарушение антимонопольных законов может повлечь за собой не только корпоративные штрафы, но и тюремное заключение высших должностных лиц компании.
Все это не означает, что компании не пытаются применять незаконные методы и избежать наказания за это. В 1996 году ведущая американская компания по переработке сельскохозяйственной продукции Archer Daniels Midland (ADM) и ее японский партнер, компания Ajinomoto, были пойманы на таком сговоре. Они заключили соглашение о разделе рынка и о ценообразовании по различным продуктам, таким как лизин (который производится из кукурузы и используется в целях обогащения корма для кур и свиней). Цель соглашений заключалась в том, чтобы поддерживать высокие цены в ущерб потребителям. Эти компании руководствовались в своих действиях таким принципом: «Конкуренты – это наши друзья, а потребители – наши враги». Неправомерные действия компаний были обнаружены благодаря тому, что один из участников переговоров со стороны ADM стал информатором ФБР и сделал много аудиозаписей и даже несколько видеозаписей встреч между представителями компаний[100].
Самый известный случай нарушения антимонопольных законов, который используется в школах бизнеса в качестве учебного примера, произошел на рынке больших турбин для производства электроэнергии. В 1950-х годах на американском рынке турбин работали три компании: GE[101] была самой крупной из них – на ее долю приходилось 60 процентов рынка; Westinghouse – около 30 процентов рынка и Allied-Chalmers – около 10 процентов. Они сохраняли за собой эти рыночные доли и поддерживали высокие цены с помощью тщательно продуманной схемы координации действий. Вот как она работала. Электроэнергетические компании объявляли тендер на турбины, которые они собирались покупать. Если приглашение на участие в тендере поступало с 1-го по 17-й день лунного месяца, Westinghouse и Allied-Chalmers должны были выставить очень высокие цены на свои турбины, с тем чтобы их предложения наверняка проиграли тендер, а GE по взаимному сговору становилась победителем тендера, предложив самую низкую цену (которая была все же монопольной ценой, обеспечивающей высокую прибыль). Точно так же компания Westinghouse становилась заранее известным победителем, если приглашение на тендер поступало с 18-го по 25-й лунный день, и Allied-Chalmers – с 26-го по 28-й лунный день. Поскольку электроэнергетические компании рассылали приглашения на участие в тендере не по лунному календарю, со временем каждый из производителей получал свою долю на рынке. Любая попытка нарушить договоренность сразу же была бы замечена конкурентами. Однако, поскольку сотрудникам Министерства юстиции даже не пришло в голову привязывать победителей тендера к лунному циклу, этот сговор был защищен от угрозы обнаружения. В итоге органы власти все-таки разобрались в ситуации, некоторые руководители этих трех компаний были приговорены к тюремному заключению, а столь прибыльный сговор провалился. Впоследствии предпринимались и другие попытки применить различные схемы сговора[102].
В 1996–1997 годах вариант схемы с турбинами использовали в процессе подачи заявок на участие в аукционе лицензий на частоты мобильной связи. Компания, которая хотела получить лицензию на использование частоты в том или ином городе, сообщала другим о своем решении бороться за эту лицензию, указав телефонный код этого города в качестве последних трех цифр предлагаемой цены. Другие компании давали ей возможность выиграть аукцион. При условии, что одна и та же группа компаний принимает участие в большом числе таких аукционов на протяжении длительного периода, а также что антимонопольные органы не обнаружат схему, она может действовать достаточно долго[103].
Однако гораздо чаще компании той или иной отрасли предпринимают попытки достичь негласного соглашения, или соглашения по умолчанию, не поддерживая непосредственных контактов. Это исключает риск уголовного преследования за нарушение антимонопольного законодательства, хотя в распоряжении антимонопольных органов есть и другие меры, направленные на разрушение даже негласного сговора. Сложность этой ситуации заключается в том, что такое соглашение не совсем понятно его участникам, а попытки нарушить его трудно обнаружить. Тем не менее компании в состоянии найти способ преодолеть и то и другое.
Вместо установления фиксированных цен они могут договориться о разделе рынка по территориальному признаку, по категории продуктов или по любому другому признаку такого рода. В этом случае обман заметить гораздо легче: ваши продавцы сразу же узнают о том, что конкурирующая компания отняла у вас часть рынка.
Процесс обнаружения факта снижения цен (особенно в розничной торговле) можно упростить, а возмездие сделать быстрым и автоматическим с помощью таких схем, как обещания не уступать и даже превзойти конкурентов и создать самые благоприятные условия для потребителей. Многие компании по продаже электронных приборов и других товаров для дома во всеуслышание заявляют, что продадут свой продукт по цене ниже цены любого конкурента. Некоторые из них даже обещают, что если вы найдете более низкую цену на тот же продукт в течение месяца после его покупки, то они возместят вам разницу или даже удвоят сумму. На первый взгляд может показаться, что такие стратегии стимулируют конкуренцию, гарантируя низкие цены. Однако даже поверхностный анализ этой ситуации с точки зрения теории игр показывает, что в действительности эти стратегии могут иметь прямо противоположный эффект. Предположим, компании Rainbow’s End и B. B. Lean взяли такую стратегию на вооружение и договорились назначить на свои рубашки цену 80 долларов. Теперь каждая из них знает, что, если она снизит цену до 70 долларов, конкурент сразу же узнает об этом. На самом деле самая большая хитрость этой стратегии состоит в том, что она перекладывает задачу раскрытия обмана на потребителей, которые больше всего заинтересованы в обнаружении низких цен. А потенциальный нарушитель договоренности тоже знает, что его конкурент может незамедлительно принять ответные меры, снизив свои цены, – для этого даже не нужно ждать выхода каталога на следующий год.
Обещания не уступать и даже превзойти конкурентов по цене или качеству продукции могут быть достаточно изощренными и уклончивыми. В ходе конкурентной борьбы между Pratt & Whitney (P&W) и Rolls-Royce (RR) за поставку реактивных авиационных двигателей для самолетов Boeing 757 и Boeing 767 компания P&W обещала всем потенциальным покупателям, что ее двигатели будут на восемь процентов более экономичными с точки зрения расхода топлива, чем двигатели RR, в противном случае P&W возместит разницу в затратах на топливо[104].
Принцип наибольшего благоприятствования потребителям гласит, что продавец предложит самую лучшую цену всем, а не избранным потребителям. Если принимать это обещание за чистую монету, может показаться, что производители гарантируют низкие цены. Но давайте глубже проанализируем ситуацию. Этот принцип означает, что производитель не может вести конкурентную борьбу, предлагая выборочные скидки, для того чтобы переманить клиентов от конкурента, и в то же время продавая продукцию по прежним высоким ценам постоянным клиентам. Такой производитель вынужден пойти на общее снижение цен, что обходится ему дороже, поскольку приводит к сокращению маржи прибыли по всем продажам. Как видите, это создает явное преимущество для картеля: выигрыш от обмана становится меньше, что повышает вероятность того, что картель сохранит свое влияние.
Федеральная комиссия по торговле (одна из ветвей американской системы применения антимонопольных законов) проводила расследование о применении этого принципа компаниями DuPont, Ethyl и другими производителями антидетонационных присадок к бензину. По результатам расследования комиссия пришла к выводу об антиконкурентном характере такой практики и запретила компаниям включать такие пункты в контракты с клиентами[105].
В начале этой главы мы упомянули о чрезмерном использовании рыбных ресурсов. Подобные проблемы обусловлены тем, что каждый человек стремится потреблять как можно больше ресурсов ради личной выгоды, перекладывая последствия своих действий на всех остальных людей или на будущие поколения. Профессор Калифорнийского университета Гаррет Хардин назвал этот феномен трагедией общин и использовал в качестве одного из примеров чрезмерный выпас общих пастбищ в Англии в XV и XVI столетиях[106]. Проблема чрезмерного использования общих ресурсов получила широкую известность под тем самым названием, которое и использовал Хардин, – «трагедия общин». В настоящее время заявил о себе более значительный пример этой проблемы – глобальное потепление. Никто не извлекает личной выгоды из сокращения выбросов углекислого газа, но если каждый будет преследовать только собственные интересы, от этого пострадают все.
Это и есть дилемма заключенных со многими участниками, подобная той, с которой столкнулся Йоссариан в романе «Уловка-22», стараясь не рисковать жизнью во время войны. Безусловно, общество осознаёт последствия нерешенности таких дилемм и предпринимает попытки исправить ситуацию. Но как определить, насколько они успешны?
Политолог Университета штата Индиана Элинор Остром вместе со своими коллегами и студентами провела масштабные исследования попыток решения такой дилеммы, как трагедия общин, – иными словами, проблемы рационального потребления и сохранения общественных ресурсов, а также предотвращения чрезмерной эксплуатации и быстрого истощения природных ресурсов. Исследователи изучили как успешные, так и неудачные попытки и определили предпосылки, необходимые для эффективной координации усилий в этой сфере[107].
Во-первых, должны быть установлены четкие правила в отношении членов группы игроков в данной игре – тех, кто имеет право на использование соответствующих ресурсов. Как правило, в качестве такого критерия выступает географическое положение или место постоянного проживания, а также этническая принадлежность, навыки или членство, которое может продаваться на аукционе или предоставляется за вступительный взнос[108].
Во-вторых, следует установить четкие правила, определяющие разрешенные и запрещенные действия. К числу таких правил относятся ограничения на период использования (открытый или закрытый сезон для охоты или рыбной ловли), место (фиксированный участок или ротация участков для вылова рыбы), технологию (размер рыболовных сетей) и, наконец, на количество или долю ресурса (например, количество дров, которые разрешается собрать и вынести из леса одному человеку).
В-третьих, должна быть введена прозрачная и понятная для всех сторон система штрафов за нарушение перечисленных правил. Эта система не обязательно должна представлять собой подробный свод правил; общие нормы поведения в стабильном сообществе могут быть не менее прозрачными и эффективными. Против нарушителей правил могут применяться самые разные санкции – от устного порицания или социального остракизма до штрафов, лишения будущих прав, а в некоторых крайних случаях – лишения свободы. Тяжесть каждого вида наказания тоже может быть разной, но важно придерживаться принципа постепенного ужесточения наказания. В случае первого возможного нарушения правил чаще всего применяется такой метод: установить с нарушителем прямой контакт и потребовать, чтобы он решил возникшую проблему. За первый или второй случай нарушения назначаются достаточно низкие штрафы, которые повышаются только в случае, если нарушения продолжаются или становятся более серьезными.
В-четвертых, должна быть введена эффективная система обнаружения нарушений. Лучший метод состоит в том, чтобы нарушения обнаруживались автоматически в ходе повседневной деятельности игрока. Например, рыболовная компания, у которой есть как хорошие, так и плохие участки, может организовать ротацию прав на хорошие участки. Рыболов, получивший хорошее место для вылова рыбы, сразу же заметит, использует ли это место нарушитель; он лично заинтересован в том, чтобы сообщить о нарушении остальным членам группы и добиться применения адекватных санкций против нарушителя. Еще один пример – введение требований о том, что сбор урожая в лесу или в других зонах общего пользования должен производиться только группами: так обеспечивается взаимный контроль и устраняется необходимость в найме охраны.
В некоторых случаях правила, определяющие разрешенные действия, необходимо разрабатывать, учитывая, существуют ли реалистичные способы обнаружить нарушения. Например, иногда бывает трудно контролировать размер улова, даже если рыболов имеет самые добрые намерения. Поэтому правила рыбного промысла, основанные на количестве выловленной рыбы, используются достаточно редко. Квоты на количество того или иного ресурса более эффективны в случаях, когда это количество легче отслеживать и можно точно измерить, как, например, воду, поставляемую из водохранилищ, а также собранную лесную продукцию.
В-пятых, когда создаются такие правила и системы их введения в действие, очень важно, чтобы информация об этом была доступна потенциальным пользователям ресурсов. Хотя уже после введения правил у каждого пользователя может возникнуть соблазн их нарушить, все они в равной степени заинтересованы в создании эффективной системы правил. При ее создании пользователи могут применить свои знания соответствующего ресурса и технологии его использования, знания о практической осуществимости мер по обнаружению нарушений, а также понимание степени доверия членов их группы к различным видам санкций за нарушение правил. Как показывает практика, в случае централизованного или иерархического управления многие из этих аспектов трактуются неправильно, поэтому такая система регулирования общих ресурсов неэффективна.
В целом Элинор Остром и ее коллеги оптимистично оценивают возможность эффективного решения многих проблем коллективной деятельности посредством использования информации о местных условиях и системах правил, но в то же время она предостерегает против чрезмерного перфекционизма: «Эта дилемма никогда не исчезнет, даже в тех системах, которые работают наилучшим образом. ‹…› Никакой мониторинг или применение санкций не сможет свести соблазн к нулю. Вместо того чтобы думать о преодолении трагедии общин, необходимо создать системы самоорганизации, которые справятся с этой проблемой лучше других».
Как и следовало ожидать, дилемма заключенных возникает не только у человека, но и у других биологических видов. В таких ситуациях, как постройка гнезда, добыча пищи и спасение от хищников, животное может действовать либо эгоистично (в собственных интересах и в интересах близкой родни), либо в интересах всей группы. Какие обстоятельства способствуют эффективным коллективным действиям? Биологи-эволюционисты провели исследования по этому вопросу и обнаружили ряд удивительных примеров и идей. Вот один из таких примеров[109].
Когда британского биолога Джона Холдейна спросили, станет ли он рисковать жизнью ради другого человека, он ответил: «За двух своих братьев или за восьмерых кузенов – да». У вас половина общих генов с родным братом (кроме однояйцевых близнецов) и одна восьмая – с кузеном; следовательно, такие действия увеличивают ожидаемое число копий ваших генов, которые передадутся следующему поколению. Подобное поведение совершенно оправдано с биологической точки зрения: процесс эволюции отдает ему предпочтение. Такая сугубо биологическая основа для кооперативного поведения среди близких родственников объясняет удивительное и сложное взаимодействие, которое наблюдается в колониях муравьев и роях пчел.
При отсутствии похожих генетических связей альтруизм среди животных – редкое явление. Однако взаимный альтруизм возникает и сохраняется между членами группы животных с более низкой генетической идентичностью, если взаимодействие между этими животными носит устойчивый и долгосрочный характер. Вот немного страшный, но интересный пример: летучие мыши-вампиры, обитающие в Коста-Рике, живут колониями около десяти особей, но охотятся порознь. Каждый день может оказаться для одних вампиров удачным, а для других – неудачным. Удачно поохотившиеся вампиры возвращаются в дуплистое дерево, в котором обитает их группа, и могут поделиться добычей, отрыгивая кровь, которую они принесли с охоты. Летучей мыши, которая три дня не получает свою порцию крови, грозит гибель. В колониях мышей-вампиров применяются эффективные методы взаимной страховки против такой угрозы с помощью разделения добычи[110].
Биолог Мэрилендского университета Джеральд Уилкинсон исследовал базовые причины такого поведения, собрав летучих мышей из разных мест и объединив их в одну группу. Он систематически отбирал кровь у некоторых из них и наблюдал за тем, делятся ли с ними кровью другие мыши. В итоге Уилкинсон обнаружил, что мыши делятся кровью только в случае, если один из членов группы находится на грани смерти, но не раньше. По всей вероятности, летучие мыши способны отличить реальную потребность от временного невезения. Еще более интересно то, что кровью делились между собой только те мыши, которые знали друг друга по предыдущим группам, и что они охотнее делились с теми членами группы, которые когда-то уже приходили им на помощь. Иными словами, летучие мыши способны идентифицировать других мышей и запоминать их поведение в прошлом, что приводит к формированию эффективной системы взаимного альтруизма.
Галапагосские острова – среда обитания дарвиновских вьюрков. На этих вулканических островах очень трудные условия для жизни, поэтому эволюционный отбор действует там достаточно сильно. Изменение размера клюва вьюрка даже на миллиметр может оказаться решающим фактором в борьбе за выживание[111].
На каждом из островов свои источники пищи, и клюв вьюрка отражает эти различия. На большом острове Дафне основной источник пищи – кактус. На этом острове птицы с весьма точным названием «кактусовые вьюрки» эволюционировали так, что их клюв идеально приспособлен к сбору пыльцы и нектара из цветков кактуса.
Эти птицы не ведут осознанную игру друг против друга. Тем не менее каждый вариант адаптации их клюва можно считать их стратегией. Стратегии, которые дают вьюркам преимущество в добыче пищи, обеспечивают выживание, выбор партнеров для спаривания и получение большего числа потомства. Клюв вьюрка – это результат такого сочетания естественного и полового отбора.
Однако даже если на первый взгляд все обстоит как нельзя лучше, генетика порой подбрасывает сюрпризы. Старая поговорка гласит: кто рано встает, тому бог подает. На острове Дафне именно вьюрок стал той ранней пташкой, которой достается нектар. Вместо того чтобы ждать девяти часов утра, когда цветки кактуса раскрываются сами, некоторые вьюрки попытались попробовать нечто новое. Они сами вскрывали цветки кактуса, чтобы поживиться раньше всех.
На первый взгляд может показаться, что это дает вьюркам преимущество перед соперниками, прилетающими немного позже. Единственная проблема в том, что, когда птицы вскрывают цветок, они часто обламывают рыльце. Джонатан Вейнер объясняет это так:
Рыльце – это верхушка тонкостенной трубки, которая выступает в виде длинной прямой соломинки в центре каждого цветка. Когда рыльце сломано, цветок становится бесплодным. Мужские гаметы, которые содержатся в пыльце, не могут соединиться с женскими гаметами цветка. В итоге цветок кактуса увядает, не завязав плод[112].
Если у кактуса увядает цветок, исчезает основной источник пищи кактусовых вьюрков. Можно предположить, каким будет результат такой стратегии: нет нектара, нет пыльцы, нет семян, нет плодов – и в итоге нет кактусовых вьюрков. Означает ли это, что в ходе эволюции вьюрки столкнулись с дилеммой заключенных, из-за которой этот вид может вымереть?
Анализ примера
Это не совсем так по двум причинам. Вьюрки занимают определенную территорию, а значит, эти птицы (и их потомки), если на месте их обитания не останется кактусов, могут погибнуть. В этом смысле уничтожение источника пищи для птиц, которые будут обитать в этом районе в следующем году, не стоит лишней порции пыльцы. Следовательно, у птиц с таким отклонением от нормы не окажется преимущества перед другими. Однако вывод будет иным, если эта стратегия получит широкое распространение. Вьюрки расширят поиск пищи, и даже если останутся птицы, которые будут ждать естественного раскрытия цветков, это все равно не спасет рыльца их кактусов. После этого наступит голод, и тогда больше всего шансов выжить будет у тех птиц, которые с самого начала имели сильные преимущества. В таком случае дополнительный глоток нектара сыграет решающую роль.
Здесь мы видим адаптацию по принципу опухолевых клеток. Если популяция остается маленькой, она может вымереть. Но если популяция разрастается до слишком больших размеров, эта стратегия становится самой лучшей. Поскольку такая стратегия становится выигрышной даже в относительном масштабе, единственный способ остановить этот процесс – уничтожить всю популяцию и начать все с самого начала. Если на острове Дафне совсем не останется вьюрков, больше некому будет ломать рыльца цветков и кактусы снова начнут цвести. Когда на остров прилетит пара удачливых вьюрков, у них будет возможность повторить весь процесс с самого начала.
Игра, о которой здесь идет речь, весьма напоминает дилемму заключенных, это один из вариантов игры «охота на оленя», которую проанализировал в свое время философ Жан-Жак Руссо[113]. Если во время такой охоты все участники работают вместе, чтобы поймать оленя, им это удается. Проблема возникает только тогда, когда мимо кого-то из охотников пробегает заяц. Если в погоню за зайцем бросаются слишком много охотников, оставшихся мало для того, чтобы поймать оленя. В таком случае всем лучше пуститься в погоню за зайцами. В охоте на оленя оптимальная стратегия выглядит так: преследовать оленя стоит тогда и только тогда, когда вы уверены в том, что все остальные охотники сделают то же самое. У вас нет причин не преследовать оленя, кроме случаев, когда вы не доверяете другим охотникам.
В итоге мы получаем игру в доверие. Существует два способа играть в эту игру: все действуют сообща – и жизнь прекрасна или каждый преследует только свои интересы – и жизнь становится ужасной, жестокой и короткой. Это не классическая дилемма заключенных, в которой у каждого человека есть стимул обмануть других игроков, какие бы действия они ни предпринимали. В данном случае нет никаких причин нарушать правила, если вы уверены в том, что другие поступают так же. Но доверяете ли вы им? Если даже доверяете, можете ли вы положиться на то, что они поверят вам? Или можете ли вы поверить тому, что они поверят в то, что вы доверяете им? Как сказал Франклин Рузвельт (в другом контексте), нам нечего бояться, кроме самого страха.
Для того чтобы применить свои знания о дилемме заключенных на практике, ознакомьтесь со следующими учебными примерами, приведенными в главе 14: «Сколько стоит один доллар?» и «Проблема короля Лира».
Глава 4. Прекрасное равновесие
Фред и Барни – охотники на кроликов, живущие в каменном веке. Однажды вечером, когда они вместе кутили, между ними завязался разговор о делах. Обменявшись мнениями, они поняли, что, объединив свои усилия, могли бы охотиться на гораздо большего зверя, такого как олень или бизон. Тот, кто охотится в одиночку, не может рассчитывать, что ему удастся завалить такого крупного зверя, как олень или бизон. Но если бы охотники объединились, каждый день охоты на оленя или бизона приносил бы в шесть раз больше мяса, чем день охоты на кроликов в одиночку. Такая кооперация дает большие преимущества: каждый охотник получит от охоты на крупного зверя в три раза больше мяса, чем от охоты на кроликов.
Фред и Барни договорились на следующий день поохотиться на крупного зверя и вернулись в свои пещеры. К сожалению, они слишком много выпили накануне и оба забыли, на какого зверя должны охотиться – на оленя или на бизона. Районы охоты на этих животных находятся в противоположных направлениях. В те времена не было мобильных телефонов, и все это происходило до того, как Фред и Барни стали соседями, поэтому они не могли быстро добраться до пещеры друг друга, чтобы выяснить, куда нужно идти. На следующее утро каждому предстояло самому принять решение.
Для того чтобы решить, куда идти, двум охотникам придется разыграть игру с одновременными ходами. Если мы обозначим количество мяса, которое получает каждый охотник за день охоты на кроликов, как одну единицу, тогда доля каждого из них в случае успешной координации усилий в охоте на оленя или на бизона составит три единицы. Следовательно, таблица выигрышей в этой игре выглядит так:

Эта игра значительно отличается от дилеммы заключенных, о которой шла речь в предыдущей главе. Проанализируем самое главное отличие. Оптимальный выбор Фреда зависит от того, что сделает Барни, и наоборот. Ни для одного из игроков не существует оптимальной стратегии вне зависимости от действий другого; в отличие от дилеммы заключенных в этой игре нет доминирующих стратегий. Следовательно, каждый игрок должен проанализировать возможный выбор другого игрока и с учетом этого искать свою оптимальную стратегию.
Фред размышляет следующим образом: «Если Барни пойдет туда, где пасутся олени, то мне достанется большая добыча, если я пойду туда же, если же я пойду на землю бизонов, то не получу ничего. Если Барни пойдет на землю бизонов, все должно быть наоборот. Вместо того чтобы рискнуть, отправиться в один из этих районов и обнаружить, что Барни пошел в другую сторону, не стоит ли мне поохотиться на кроликов самому, как я делал это всегда, пусть это и принесет мне меньше мяса? Иными словами, не следует ли мне взять одну единицу наверняка, вместо того чтобы рисковать и получить либо три единицы, либо ничего? Это зависит от того, что, по моему мнению, сделает Барни, поэтому мне нужно стать на его место и поразмышлять о том, что думает он. Но ведь он тоже гадает, что буду делать я, и пытается поставить себя на мое место! Есть ли конец у этих повторяющихся по кругу размышлений о размышлениях?»
Прекрасное равновесие Джона Нэша было разработано в качестве теоретического инструмента, позволяющего найти «квадратуру круга» размышлений о размышлениях по поводу выбора других игроков в стратегических играх[114]. Идея состоит в том, чтобы найти такое решение, при котором каждый участник игры выбирает стратегию, больше всего отвечающую его интересам, в ответ на стратегию другого игрока. Если в игре складывается такая ситуация, ни у одного из игроков нет причин менять свой выбор в одностороннем порядке. Следовательно, это и есть потенциально устойчивый результат игры, в которой игроки делают индивидуальный и одновременный выбор своих стратегий. Для начала проиллюстрируем эту идею на нескольких практических примерах, затем обсудим, в какой степени равновесие Нэша позволяет предсказать результаты различных игр; при этом обоснуем причины для осторожного оптимизма и для использования равновесия Нэша в качестве отправной точки анализа практически всех игр.
Проанализируем эту концепцию на примере ценовой игры между компаниями Rainbow’s End и B. B. Lean. В главе 3 у них было только два варианта цены на рубашку: 70 и 80 долларов. Каждая из компаний испытывала сильное искушение снизить эту цену. Теперь увеличим число вариантов выбора, предоставив им возможность менять цену на один доллар в более низком ценовом диапазоне, от 42 до 38 долларов[115]. В предыдущем примере говорится о том, что, если обе компании назначат цену 80 долларов, каждая из них продаст 1200 рубашек. Если одна из компаний снизит цену на один доллар, а другая оставит ее неизменной, тогда компания, снизившая цену, привлечет 100 покупателей: 80 покупателей, перешедших от какой-либо другой компании, и 20 новых – это могут быть покупатели, которые решат приобрести рубашку, которую не купили бы по более высокой цене. Если обе компании снизят цену на один доллар, имеющиеся покупатели не станут менять свои привычки, но у каждой компании появится 20 новых покупателей. Следовательно, если обе компании назначат цену 42 доллара вместо 80, каждая из них получит 38 × 20 = 760 покупателей сверх первоначальных 1200. В этом случае каждая компания продаст по 1960 рубашек и получит прибыль (42–20) × 1960 = 43 120 долларов. Выполнив аналогичные расчеты для других комбинаций цен, получим следующую таблицу выигрышей для этой игры:
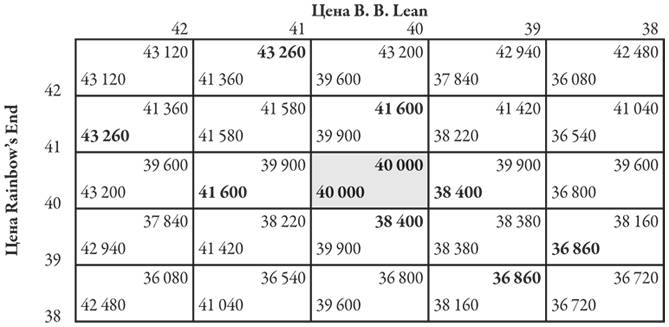
ЗАДАЧА ДЛЯ ТРЕНИРОВКИ МЫШЛЕНИЯ № 2
Попробуйте построить эту таблицу в Excel.
Ответ вы сможете найти в конце книги, в разделе «Решения».
Эта таблица может показаться сложной, но на самом деле построить ее очень легко с помощью Microsoft Excel или любой другой программы табличных вычислений.
Проанализируем ход мыслей менеджеров RE, отвечающих за установление цен. (С этого момента будем для краткости говорить «ход мыслей RE» и «ход мыслей BB».) Если RE считает, что BB выберет цену 42 доллара, тогда прибыль RE в случае выбора других возможных цен отображена в левом нижнем углу каждой ячейки первого столбца прибылей в представленной таблице. Максимальное из этих пяти чисел – 43 260 долларов, что соответствует цене 41 доллар. Следовательно, это и есть оптимальный ответный ход RE в случае, если BB выберет 42 доллара. Точно так же можно определить следующие оптимальные ходы RE: 40 долларов в случае, если, по мнению RE, компания BB выберет 41, 40 или 39 долларов, и 39 долларов – если BB выберет 38 долларов. Для наглядности мы выделили эти цифры в таблице жирным шрифтом. Оптимальные ответные ходы BB на различные варианты выбора RE показаны в верхних правых углах соответствующих ячеек и тоже выделены жирным шрифтом.
Прежде чем двигаться дальше, сделаем два замечания об оптимальных ответных ходах. Во-первых, необходимо внести ясность в значение самого термина. В данном примере две компании делают свой выбор одновременно. Следовательно, в отличие от ситуации в главе 2 каждая компания не может увидеть выбор другой стороны, чтобы ответить на него своим оптимальным ходом, выбранным с учетом решения первой компании. Вместо этого обе компании формирует свою субъективную оценку (которая может основываться на размышлениях, на опыте или на обоснованных предположениях) по поводу того, каким может быть выбор другой компании, и делает ответный ход в соответствии с этой оценкой.
Во-вторых, не всегда самое лучшее решение состоит в том, чтобы продавать свою продукцию по более низкой цене, чем другая компания. Если RE считает, что BB выберет 42 доллара, RE следует выбрать более низкую цену, а именно 41 доллар. Однако если RE считает, что BB выберет 39 долларов, лучший ответный ход RE – более высокая цена, 40 долларов. Выбирая оптимальную цену, компания RE должна учесть два противоположных соображения: продажа продукции по более низкой цене, чем у BB, позволит RE увеличить объем сбыта, но маржа прибыли на единицу проданной продукции снизится. Если RE считает, что BB назначит очень низкую цену, тогда снижение маржи прибыли RE на единицу продукции из-за продажи товаров по цене ниже BB может оказаться слишком большим, поэтому для RE может быть выгоднее пойти на сокращение объема сбыта, чтобы получить более высокую маржу прибыли на каждую проданную рубашку. В самом крайнем случае, если RE считает, что BB будет продавать рубашки по себестоимости, составляющей 20 долларов, установление такой же цены не принесет RE никакой прибыли. Следовательно, RE лучше выбрать более высокую цену, сохранить при этом часть лояльных потребителей и получить от них хотя бы какую-то прибыль.
Вернемся к таблице и внимательно изучим оптимальные ответные ходы каждой компании. Сразу же обращает на себя внимание следующий факт: в одной из ячеек (той, в которой каждая компания выбирает цену 40 долларов) выделены жирным шрифтом обе цифры, отображающие прибыль, которую может получить каждая компания, а именно 40 тысяч долларов. Если RE считает, что BB выберет цену 40 долларов, ее оптимальная цена тоже составит 40 долларов, и наоборот. Если обе компании назначат на свои рубашки цену 40 долларов, субъективная оценка каждой из этих компаний в отношении цены другой компании будет подтверждена фактическим результатом. В таком случае у одной компании не будет причин для изменения цены, если ей станет известна информация о том, какую цену выбрала другая компания. Следовательно, эти варианты выбора образуют в данной игре устойчивую конфигурацию.
Такой результат игры, при котором каждый игрок предпринимает действия, оптимальные с точки зрения его субъективной оценки действий другого игрока, а действия всех игроков соответствуют такой субъективной оценке, и есть та самая «квадратура круга» размышлений о размышлениях. Следовательно, этот результат можно смело назвать точкой покоя в размышлениях игроков, или равновесием данной игры. Собственно говоря, это и есть определение равновесия Нэша.
Для того чтобы отметить равновесие Нэша в данном примере, мы выделили соответствующую ячейку таблицы серым цветом; то же самое будем делать и в следующих таблицах.
Описанная в главе 3 ценовая игра, в которой было только два варианта цен (80 и 70 долларов), – это пример дилеммы заключенных. Более общая игра с несколькими вариантами цен относится к той же категории игр. Если бы две компании смогли заключить достоверный осуществимый договор о согласованных действиях, это позволило бы обеим назначить на свою продукцию гораздо более высокую цену, чем 40 долларов, которую предлагает равновесие Нэша, и это обеспечило бы им обеим более высокую прибыль. Как мы определили в главе 3, если обе компании назначат на свою продукцию цену 80 долларов, они заработают по 72 тысячи долларов против 40 тысяч, полученных согласно равновесию Нэша. Это означает, что потребители могут оказаться в крайне невыгодном положении, если в какой-то отрасли сформируются монополия или картель производителей.
В приведенном примере у обеих компаний были симметричные позиции в отношении таких показателей, как себестоимость и число проданных единиц продукции по каждой комбинации цен. В общем случае не обязательно должно быть именно так: тогда будет получено равновесие Нэша с разными ценами у двух компаний. Тем из вас, кто хочет лучше овладеть всеми этими методами и концепциями, предлагаем решить следующую задачу (желающие могут посмотреть ответ в разделе «Решения»).
ЗАДАЧА ДЛЯ ТРЕНИРОВКИ МЫШЛЕНИЯ № 3
Предположим, компания Rainbow’s End нашла поставщика более дешевых рубашек, поэтому ее цена снизилась с 20 до 11,6 доллара, тогда как в B. B. Lean осталась прежняя цена – 20 долларов. Сделайте перерасчет таблицы выигрышей и найдите новое равновесие Нэша.
У ценовой игры есть много других аспектов, но они более сложны, чем тот материал, который мы рассматривали до настоящего момента. Поэтому проанализируем эти аспекты далее в данной главе. В заключение текущего раздела сделаем несколько общих комментариев по поводу равновесия Нэша.
Есть ли равновесие Нэша в каждой игре? Ответ: в большинстве случаев да, при условии, что мы обобщим концепцию действий или стратегий, разрешив смешивание ходов. Именно это условие было указано в знаменитой теореме Нэша. Мы рассмотрим концепцию смешивания ходов более подробно в следующей главе. Игры, в которых нет равновесия Нэша даже в случае смешивания ходов, настолько сложны или трудны для понимания, что их углубленное изучение под силу только специалистам по теории игр.
Можно ли считать равновесие Нэша эффективным решением в играх с параллельными ходами? Некоторые аргументы и доказательства по этому вопросу изложены в данной главе далее, и наш ответ будет сдержанно-утвердительным.
Есть ли в каждой игре единственное равновесие Нэша? Нет. Рассмотрим ряд важных примеров игр с несколькими равновесиями Нэша, а также проанализируем новые вопросы, возникающие в связи с этим.
Давайте попробуем применить теорию Нэша к игре в охоту. Найти оптимальные ответные ходы в этой игре достаточно легко. Фреду следует просто сделать тот же выбор, который, по его мнению, сделает Барни. Вот каким будет результат:
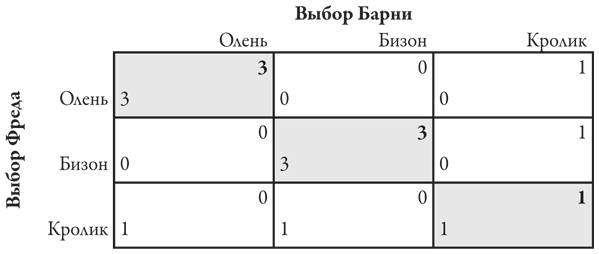
Следовательно, в этой игре есть три равновесия Нэша[116]. Какое из них выберут в итоге оба игрока? Или они вообще не смогут достичь равновесия в этой игре? Концепция равновесия Нэша сама по себе не дает ответов на эти вопросы. Для этого необходим дополнительный анализ, основанный на других рассуждениях.
Если бы Фред и Барни встретились на холостяцкой вечеринке[117], которую устроил их общий друг, выбор охоты на оленя оставил бы более заметный след в их памяти. Если бы согласно обычаям их общины глава семьи говорил, отправляясь на охоту: «Пока, сынок»[118], – более очевидным для них был бы выбор охоты на бизона. Но если бы в семье было принято говорить на прощание: «Береги себя», – более значимым был бы безопасный выбор, гарантирующий хотя бы какое-то количество мяса независимо от выбора другого охотника, а именно охота на кролика.
А что именно представляет собой эта «значимость»? Одна стратегия, скажем, охота на оленя, может быть значимой для Фреда, но этого недостаточно для того, чтобы он выбрал именно ее. Он должен спросить себя, является ли эта стратегия столь же значимой для Барни. А это, в свою очередь, поднимет вопрос о том, считает ли Барни эту стратегию значимой для Фреда. Выбор одного из нескольких равновесий Нэша требует решения той же задачи с размышлениями о размышлениях, что и сама концепция равновесия Нэша.
Для того чтобы такая «значимость» позволяла решить эту задачу, она должна включать в себя несколько уровней. Успешный выбор одного из равновесий Нэша в ситуации, когда оба игрока размышляют и действуют изолированно друг от друга, сводится к такой цепочке рассуждений: для Фреда должно быть очевидным, что для Барни очевидно, что для Фреда очевидно… что это правильный выбор. Если равновесие подразумевает выбор, очевидный до бесконечности в данном смысле, иными словами, если на нем сходятся ожидания игроков, мы называем это фокальной точкой. Это одна из нескольких новаторских концепций, которые ввел в теорию игр Томас Шеллинг.
Существование такой фокальной точки в игре зависит от многих условий, самое важное из которых – общий опыт игроков, который может быть историческим, культурным, лингвистическим или совершенно случайным. Вот несколько примеров, иллюстрирующих эту идею.
Начнем с одного из классических примеров Шеллинга. Предположим, вам сказали, что вы должны встретиться с кем-то в Нью-Йорке в назначенный день, но не сказали, где и когда. Вы даже не знаете, с кем именно вы должны встретиться, поэтому не можете связаться с этим человеком заранее (но вам сказали, что вы узнаете друг друга, когда встретитесь). Вам сказали также, что другой человек получил те же инструкции.
На первый взгляд ваши шансы на успех могут показаться довольно низкими: Нью-Йорк – огромный город, да и день длится долго. Но на самом деле многие люди успешно решают эту задачу. Со временем встречи все просто: полдень – это очевидная фокальная точка; ожидания сходятся на ней почти инстинктивно. С местом встречи немного сложнее, но в Нью-Йорке не так много ориентиров, на которых могут сойтись ожидания игроков. Это существенно сужает диапазон выбора и повышает вероятность успешной встречи.
Томас Шеллинг провел эксперименты с участием людей, приехавших из Бостона и Нью-Хейвена. В те времена эти люди должны были отправиться в Нью-Йорк поездом и приехать на Центральный вокзал; для них фокальной точкой были бы часы на этом вокзале. В наши дни многие люди выбрали бы в качестве места встречи Эмпайр-Стейт-билдинг – возможно, из-за фильма Sleepless in Seattle («Неспящие в Сиэтле») или An Affair to Remember («Незабываемый роман»). Для других очевидным «перекрестком миров» стала бы площадь Таймс-сквер.
Один из нас (Барри Нейлбафф) провел этот эксперимент в рамках ТВ-шоу Primetime на канале АВС, в программе под названием Life: The Game («Жизнь – игра»)[119]. Шесть пар совершенно незнакомых людей отвезли в разные районы Нью-Йорка и попросили найти другие пары, не имея никакой информации, за исключением того, что другая пара будет искать их на тех же условиях. Обсуждение плана действий проходило в каждой паре в полном соответствии с логикой Шеллинга. Каждая пара анализировала, каким может быть очевидное место встречи, а также что думают по этому поводу участники другой пары. Одна команда (скажем, команда А) пришла в своих рассуждениях к выводу о том, что другая команда (команда Б) тоже в это же время размышляла о том, что очевидно для команды А. В итоге три пары прибыли к Эмпайр-Стейт-билдинг и еще три пары – на Таймс-сквер. Все пары выбрали полдень в качестве времени встречи. Но им предстояло разобраться еще с некоторыми вопросами: в Эмпайр-Стейт-билдинг две смотровые площадки на разных уровнях, а Таймс-сквер – очень большая площадь. Однако участники эксперимента проявили находчивость (в том числе использовали таблички с надписями), благодаря чему всем шести парам удалось найти друг друга[120].
Для успешного решения такой задачи важно не то, что место очевидно для вас или для других игроков, а то, что для каждого из вас очевидно, что для других очевидно, что… И если Эмпайр-Стейт-билдинг соответствует этому критерию, значит каждая команда должна отправиться именно туда, даже если кому-то не совсем удобно туда добираться, поскольку это единственное место, в котором каждая команда может рассчитывать найти другую. Если бы в игре участвовали только две команды, одна из них могла бы подумать, что очевидная фокальная точка – это Эмпайр-Стейт-билдинг, а другая – что Таймс-сквер столь же очевидное место встречи; в таком случае эти две команды не смогли бы встретиться.
Профессор Дэвид Крепс из Стэнфордской школы бизнеса провел на занятиях следующий эксперимент. Каждый из двух студентов должен был сделать выбор, не имея возможности обменяться информацией с другим студентом. Их задача состояла в том, чтобы разделить между собой список городов. Одному студенту достался Бостон, другому – Сан-Франциско (эта информация была открытой, так что оба знали города друг друга). Затем каждому дали список из девяти американских городов (Атланта, Чикаго, Даллас, Денвер, Хьюстон, Лос-Анджелес, Нью-Йорк, Филадельфия и Сиэтл) и предложили выбрать несколько из этих городов. Если студенты получали в результате два непересекающихся подмножества городов, каждому из них давали приз. Но если в их общем списке не хватало одного города или были повторения, они оба ничего не получали.
Сколько равновесий Нэша существует в этой игре? Если студент, за которым закреплен Бостон, выберет, скажем, Атланту и Чикаго, а студент, которому достался Сан-Франциско, – остальные города (Даллас, Денвер, Хьюстон, Лос-Анджелес, Нью-Йорк, Филадельфию и Сиэтл), это и есть равновесие Нэша: учитывая выбор одного игрока, любое изменение выбора, сделанного другим игроком, приведет либо к пропуску, либо к совпадению городов в их списках и снизит выигрыш того, кто отклонился от равновесия. Такая же аргументация применима в случае, если один студент выберет Даллас, Лос-Анджелес и Сиэтл, а другой – шесть оставшихся городов. Иными словами, в данной игре существует столько равновесий Нэша, сколько существует способов разделить список из девяти чисел на два разных подмножества. Существует 29 = 512 таких способов; следовательно, в данной игре присутствует огромное число равновесий Нэша.
Могут ли у участников этой игры сойтись ожидания, которые создадут фокальную точку? Если оба игрока были американцами или жили в США уже достаточно долго, в 80 процентах случаев они делили список по географическому принципу: студенты, за которыми был закреплен Бостон, выбирали города, расположенные к востоку от Миссисипи, а студенты, за которыми был закреплен Сан-Франциско, – к западу[121]. Такая координация была гораздо менее вероятной, если один или оба студента не являлись гражданами США. Следовательно, национальность или культура могут способствовать созданию фокальной точки. Когда в ходе эксперимента Крепса у пар студентов не было общего опыта, порой они выбирали города по алфавиту, но даже в этом случае отсутствовала очевидная точка раздела. Если бы общее число городов в списке было четным, фокальной точкой могло бы стать разделение списка поровну, но с девятью городами сделать это невозможно. Таким образом, нельзя утверждать, что игроки всегда найдут способ выбрать одно из множества равновесий Нэша благодаря сходимости своих ожиданий; вполне возможно, что им не удастся найти фокальную точку[122].
Далее предположим, что каждому из двух игроков предложили выбрать натуральное число. Если оба игрока выбирают одно и то же число, каждый из них получает приз. Если оба выбирают разные числа, они не получают ничего. В подавляющем большинстве случаев выбор выпадает на число 1: это первое число ряда целых (натуральных) чисел; это наименьшее число и так далее; следовательно, оно и есть фокальная точка. В данном случае причины, по которым это число выделяется среди других чисел, носят сугубо математический характер.
Томас Шеллинг приводит в качестве иллюстрации пример, когда двое или больше людей приходят вместе в людное место и теряют друг друга. Куда должен пойти каждый из них, чтобы встретиться с остальными? Если бы в таком месте, скажем в универмаге или на железнодорожном вокзале, было специальное окошко под названием «Потерявшиеся» или «Найденные», оно вполне могло бы стать фокальной точкой. В данном случае причины того, что мост заметен, носят лингвистический характер. Иногда места встречи создаются специально для того, чтобы обеспечить сходимость ожиданий. Например, в Германии и Швейцарии на многих вокзалах выделены места с хорошо заметными указателями Treffpunkt («Место встречи»).
В игре во встречу замечательно не только то, что в ней два игрока находят друг друга, но и то, что фокальная точка играет большую роль во многих других случаях стратегического взаимодействия. Один из самых важных примеров такого взаимодействия – Фондовый рынок. Джон Мейнард Кейнс – пожалуй, самый известный экономист ХХ столетия – объяснял поведение фондового рынка, проводя аналогию с популярным в те времена газетным конкурсом. Во время такого конкурса в газете печаталось несколько фотографий лиц, а читатели должны были угадать, какое именно лицо посчитает самым красивым большинство участников голосования[123]. В этой ситуации логика рассуждений сводится к следующему: о каком лице большинство людей подумают, что большинство других людей подумают, что большинство других подумают… что оно самое красивое. Если бы лицо одного из участников конкурса было существенно красивее всех остальных, оно и стало бы необходимой фокальной точкой. Но задача читателей редко бывала столь простой. Представьте себе, что есть сотня финалистов конкурса, которых почти невозможно отличить друг от друга, разве что по цвету волос. Из сотни финалистов только у одного рыжие волосы. Вы выбрали бы рыжеволосого?
Следовательно, задача состоит не в том, чтобы составить однозначное мнение о красоте, а в том, чтобы найти фокальную точку этих размышлений. Как же достичь согласия в этом? Читатели должны найти такое согласие, не имея возможности общаться друг с другом. Можно рассуждать по принципу «выбрать самого красивого человека», но сделать это гораздо труднее, чем выбрать рыжеволосого человека, или человека с симпатичной щелью между передними зубами (как у Лорен Хаттон), или человека с родинкой (как у Синди Кроуфорд). Все, что отличает человека от других, становится фокальной точкой и обеспечивает сходимость ожиданий. Именно поэтому не стоит удивляться, что многие из лучших моделей мира не обладают совершенной внешностью; они скорее почти идеальны, но у них есть какой-либо милый изъян, который придает их внешнему виду индивидуальность и привлекает к себе всеобщее внимание, а значит, играет роль фокальной точки.
Кейнс использовал конкурсы красоты как метафору для фондового рынка, где каждый инвестор стремится купить акции, которые вырастут в цене, а значит, акции, курс которых повысится, по мнению широкого круга инвесторов. «Горячие» акции – это акции, по поводу которых все думают, что все думают… что это «горячие» акции. Тот факт, что акции разных компаний пользуются повышенным спросом в разное время, объясняется разными причинами, такими как хорошо разрекламированное первичное размещение акций, рекомендация известного аналитика и так далее. Концепция фокальной точки позволяет объяснить, почему такое большое внимание привлекают к себе круглые числа, например 10 000 в случае индекса Доу-Джонса или 2500 в случае индекса NASDAQ. Эти индексы рассчитываются на основании стоимости акций, входящих в состав соответствующего портфеля. Число 10 000 не имеет никакого внутреннего значения; оно служит в качестве фокальной точки только потому, что ожидания чаще сходятся на круглых числах.
Смысл всего сказанного состоит в том, что равновесие вполне может быть выбрано под влиянием порыва. Не существует фундаментального закона, который гарантировал бы, что будет выбрана самая красивая участница конкурса красоты или что лучшие акции будут расти в цене быстрее всех. Есть только факторы, которые способствуют этому. Высокая прогнозируемая прибыль на акцию – это то же самое, что внешность участницы конкурса красоты: одно из множества необходимых, но ни в коем случае не достаточных условий, требуемых для того, чтобы обуздать не поддающиеся контролю порывы и предпочтения.
Многим специалистам по теории математических игр не нравится зависимость исхода игры от исторических, культурных или лингвистических факторов или от условных инструментов, таких как круглые числа. Они предпочли бы, чтобы решение зависело только от абстрактных математических фактов об игре, таких как число игроков, стратегии, имеющиеся в распоряжении каждого из них, а также выигрыш каждого игрока в зависимости от стратегии, выбранной другими игроками. Мы не согласны с этой точкой зрения. Мы считаем закономерным тот факт, что исход игры, в которую играют люди, взаимодействующие друг с другом в обществе, зависит от социальных и психологических аспектов этой игры.
Возьмем в качестве примера ведение переговоров по поводу заключения той или иной сделки. В этом случае интересы игроков совершенно несовместимы: большая доля для одного означает меньшую долю для другого. Однако во многих случаях, если сторонам не удается договориться, обе не получают ничего и могут понести серьезные убытки – например, когда срываются переговоры по поводу заработной платы, после чего начинается забастовка или наступает локаут (временная остановка работы по инициативе работодателя). Интересы обеих сторон таких переговоров совпадают в том смысле, что обе стремятся избежать подобных разногласий. Они могут сделать это, если найдут фокальную точку, а также если каждая сторона считает, что другая больше ничего не уступит. Именно поэтому так часто встречается вариант разделения 50:50. Это простой и понятный вариант, у которого есть одно важное преимущество: он кажется справедливым. Кроме того, при наличии таких соображений этот вариант обеспечивает сходимость ожиданий.
Рассмотрим в качестве примера проблему чрезмерно высокой оплаты труда генеральных директоров компаний – CEO. Во многих случаях СЕО действительно заботятся о своей репутации. Получит ли такой человек 5 или 10 миллионов долларов, на самом деле не окажет большого влияния на его жизнь. (Нам легко так говорить, поскольку для нас обе цифры не более чем абстракция.) Какое же «место встречи» интересует большинство СЕО? Быть исключительным. Каждый стремится оказаться в верхней половине лучших. Все СЕО хотят «встретиться» именно там. Проблема в том, что это «место встречи» может вместить в себя только половину желающих. Но они обходят эту проблему благодаря повышению заработной платы. Каждая компания платит своему СЕО больше средней заработной платы топ-менеджеров за предыдущий год, чтобы все думали, будто у них исключительный генеральный директор. В итоге происходит необоснованное повышение заработной платы СЕО до чрезвычайно высокого уровня. Для того чтобы решить эту проблему, необходимо найти другую фокальную точку. Например, в прошлом СЕО компаний заслуживали серьезную репутацию благодаря бескорыстному служению обществу. Соперничать в этом направлении – хорошая мысль во всех отношениях. Текущая фокальная точка в плане оплаты труда топ-менеджеров сформировалась под влиянием опросов Business Week и консультантов по вопросам бизнеса. Изменить эту ситуацию будет нелегко.
Вопрос справедливости – это также вопрос выбора фокальной точки. В Декларации целей развития на пороге тысячелетия, а также в книге Джеффри Сакса The End of Poverty[124] говорится о том, что, если выделить на развитие всего один процент ВВП, можно к 2025 году покончить с нищетой. Главное здесь то, что фокальная точка вклада в развитие выражена в процентах от доходов, а не в абсолютном значении. Это означает, что богатые страны должны сделать более весомый вклад, чем бедные. Очевидная справедливость этого принципа может обеспечить сходимость ожиданий в данном вопросе. Но будут ли обещанные средства действительно выделены, остается только гадать.
В охотничьей игре интересы двух игроков полностью совпадают: оба отдают предпочтение одному из двух вариантов равновесия в охоте на крупного зверя, а единственная проблема заключается в том, чтобы их субъективные оценки сошлись в фокальной точке. Теперь проанализируем еще две игры, в которых тоже есть не одно равновесие Нэша, но присутствует конфликт интересов. Каждая из этих игр позволяет почерпнуть интересные идеи по поводу стратегии.