Задание 6. Выбор оптимального варианта
6.1. Общие вопросы
В спецификации контрольных измерительных материалов для проведения в 2023 году единого государственного экзамена по МАТЕМАТИКЕ (базовый уровень) в качестве проверяемого результата обучения применительно к заданию 6 указывается «умение извлекать информацию, представленную в таблицах, на диаграммах, графиках».
Уровень сложности – базовый.
Максимальный балл за выполнение задания – 1.
Примерное время выполнения задания выпускником (мин.) – 11.
Чтобы решить задание 6 по математике базового уровня необходимо уметь:
• собирать комплект,
• выбирать наилучший варианта из двух/трех/четырех возможных вариантов.
6.2. Примеры заданий и методика их выполнения
Условие
Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.

Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день.
В ответе укажите какой-нибудь один набор номеров переводчиков (без пробелов, запятых и других дополнительных символов)
Решение
Для решения данного задания необходимо собрать комплект из четырех переводчиков, при этом суммарная стоимость их услуг не должна превышать 12 000 рублей в день. Таким образом, переберем все возможные варианты:
• 1 (Немецкий, испанский), 3 (Английский), 5 (Французский): 7000 + 3000 + 2000 = 12000;
• 1 (Немецкий, испанский), 4 (Английский, французский): 7000 + 6000 = 13000;
• 2 (Английский, немецкий), 5 (Французский), 6 (Испанский): 6000 + 2000 + 4000 = 12000.
Другие комбинаций составить невозможно.
Очевидно, нам подходят комбинация 135 и 256. При этом ответ предполагает любую из данных комбинаций, также цифры могут быть тоже записаны в любом порядке.
Ответ: 135 < или > 153 < или > 315 < или > 513 < или > 531 < или > 256 < или > 265 < или > 526 < или > 562 < или > 625 < или > 652.
Условие
В таблице приведены данные о шести чемоданах.
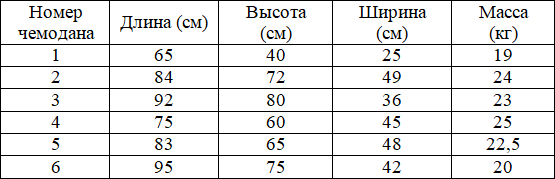
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 203 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании? В ответе укажите номера всех выбранных чемоданов (без пробелов, запятых и других дополнительных символов).
Решение
В первую очередь необходимо выбрать чемоданы, вес которых удовлетворяет условию, т.е., не больше 23 кг. Это чемоданы под номером 1, 3, 5 и 6. После чего выполним сложение их величин (длины, ширины и высоты) и сравним с числом 203:
Чемодан № 1: 65 + 40 + 25 = 130 < 203
Чемодан № 3: 92 + 80 + 36 = 208 > 203
Чемодан № 5: 83 + 65 + 48 = 196 < 203
Чемодан № 6: 95 + 75 + 42 = 212 > 203
Таким образом, нам подходят чемодан под номером 1 и 5.
Ответ: 15 < или > 51.
Условие
Строительная фирма планирует купить 70 м3 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице.

Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
Решение
Поочерёдно вычислим сколько нужно будет заплатить каждому из поставщиков за 70 м3 пеноблоков:
Поставщик А: 2600∙70 = 182000
С учётом доставки: 182000 + 10000 = 192000
Поставщик Б: 2800∙70 = 196000
Доставка бесплатная, так как сумма товара свыше 150000
Поставщик В: 2700∙70 = 189000
С учётом доставки: 189000 + 8000 = 197000.
Очевидно, что самый дешёвый вариант – это заказать 70 м3 пеноблоков у поставщика А за 192000 руб.
Ответ: 192000.
Условие
Рейтинговое агентство определяет рейтинг электрических фенов для волос на основе средней цены P (в рублях за штуку), а также показателей функциональности F, качества Q и дизайна D. Рейтинг R вычисляется по формуле
R = 3(F + Q) + D–0,01P.
В таблице даны цены и показатели четырёх моделей фенов.

Найдите наименьший рейтинг фена из представленных в таблице моделей.
Решение
Поочерёдно вычислим рейтинг каждого представленного в таблице фена:
Фен А: R = 3(3 + 4) + 2–0,01∙2100 = 23–21 = 2
Фен Б: R = 3(4 + 3) + 1–0,01∙2200 = 22–22 = 0
Фен В: R = 3(4 + 3) + 0–0,01∙2000 = 21–20 = 1
Фен Г: R = 3(2 + 4) + 1–0,01∙1700 = 19–17 = 2.
Наименьший рейтинг у фена Б, он равен 0.
Ответ: 0.