1. Линейная регрессионная модель
Для начала введем некоторые обозначения. Предположим, что некоторая величина Y зависит от величин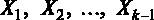 
. Введем понятие регрессионного уравнения – это уравнение вида 
, где 
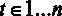. Через n обозначим число наблюдений, по которым строится регрессия, k – число регрессоров в модели, 
– случайная величина, которая носит название ошибки регрессии.
Модель такого вида называется классической линейной регрессионной моделью (ЛРМ) в случае, если выполняются следующие предпосылки:
1. , 
– линейная спецификация модели, где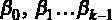 
– коэффициенты модели, которые подлежат определению, , 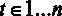– ошибки модели.
2. 
, 
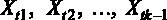– детерминированные величины.
3. 
– математическое ожидание ошибок равно нулю, 
, дисперсия ошибок не зависит от номера наблюдения.
4. 
, 
– совместное математическое ожидание ошибок разных наблюдений равно нулю.
5. Если выполняется дополнительная предпосылка о нормальном распределении ошибок 
, то классическая линейная регрессионная модель называется нормальной линейной регрессионной моделью (НЛРМ).
Подробнее о предпосылках линейной регрессионной модели можно прочесть в [2, 3].