Метамышление. Как нейронауки помогают нам понять себя - читать онлайн

Есть там что-нибудь – или нет? Такой вопрос встал перед Станиславом Петровым одним ранним сентябрьским утром 1983 года. Петров был подполковником ПВО советских войск и отвечал за мониторинг системы спутников раннего предупреждения. Холодная война между США и Советским Союзом находилась на пике, и угроза запуска ядерных ракет большой дальности одной из сторон была вполне реальна. В то роковое утро в командном центре Петрова сработала сигнализация, оповестившая, что пять американских ракет направляются в сторону Советского Союза. Согласно доктрине взаимного гарантированного уничтожения, задачей Петрова было немедленно сообщить об атаке своему руководству, чтобы то могло нанести контрудар. Время поджимало – через двадцать пять минут ракеты разорвались бы на советской земле[15].

Но Петров посчитал, что сигнал тревоги вряд ли вызвала настоящая ракета, и доложил о сбое системы. Он больше верил в ненадежность спутников и помехи на экране радара, чем во внезапный ракетный удар Соединенных Штатов, который несомненно бы привел к началу ядерной войны. Несколько минут нервного ожидания подтвердили его правоту. Ложная тревога стала результатом ошибки спутников, принявших солнечные блики на поверхности облаков за ракеты, несущиеся в верхних слоях атмосферы.

Петров воспринимал мир в оттенках серого и был готов усомниться в том, что говорили ему системы спутников и органы чувств. Его готовность осознать двусмысленность положения и усомниться спасла мир от катастрофы. В этой главе мы увидим, что представление о неопределенности служит ключевым ингредиентом в рецепте наших систем самосознания. Человеческий мозг представляет собой изощренный механизм для отслеживания неопределенности, которая играет в работе мозга огромную роль, а не только участвует в принятии ответственных решений, как в истории Петрова. Без способности оценивать неопределенность мы вряд ли вообще смогли бы воспринимать мир. Замечательный, хотя и побочный, эффект этой способности – неопределенностью можно пользоваться, чтобы сомневаться в самих себе.

Обратные задачи и способы их решения

Сложность задачи Петрова заключалась в том, что ему нужно было отличить сигнал радара от помех. Один и тот же след на экране мог быть как настоящей ракетой, так и сбоем системы. Понять лишь по изображению, с чем имеешь дело, невозможно. Такая задача называется обратной – потому что для ее решения необходимо развернуть причинно-следственную цепочку задом наперед и сделать предположение о причинах получаемой нами информации. Схожим образом наш мозг постоянно решает обратные задачи, не зная, что в действительности происходит в мире.

Причина в том, что мозг заперт внутри темной черепушки и контактирует с внешним миром лишь посредством ограниченной низкокачественной информации, предоставляемой органами чувств. Возьмем, к примеру, простую, на первый взгляд, задачу – определить, была ли только что вспышка света в затемненной комнате. Если сделать вспышку достаточно тусклой, то иногда может показаться, что свет горит, даже если в действительности это не так. Поскольку глаза и мозг подвержены помехам, при каждом повторении стимула нейроны в зрительной коре головного мозга возбуждаются не совсем одинаково. Иногда, даже когда свет не горит, случайные помехи приводят к высокой частоте возбуждения нейронов, подобно тому как след на экране радара Петрова стал результатом атмосферных помех. Поскольку мозг не знает, вызвана ли эта высокая частота стимулом или помехами, то, когда нейроны зрительной коры активно возбуждаются, будет казаться, что свет зажжен[16].

Так как каждое из наших чувств – осязание, обоняние, вкус, зрение и слух – имеет доступ лишь к небольшому, искаженному кусочку реальности, им необходимо объединить ресурсы, чтобы выдвинуть наилучшее предположение о том, что же на самом деле происходит. Наши чувства похожи на слепцов из древней индийской притчи. Тот, кто держит слона за ногу, говорит, что, должно быть, слон – это столб; тот, кто ощупывает хвост, говорит, что слон похож на веревку; тот, кто трогает хобот, говорит, что он похож на ветку дерева; тот, кто прикасается к уху, считает, что он напоминает веер; тот, кто ощупывает живот слона, – что он вроде стены; а тот, кто изучает бивень, – что он похож на массивную трубу. В конце концов проходящий мимо незнакомец сообщает им, что на самом деле они все правы – у слона есть все описанные черты. Лучше бы им объединить свои наблюдения, говорит он, а не спорить.

Математическая формула, известная как теорема Байеса, – мощный инструмент для осмысления такого рода проблем.

Чтобы увидеть, как она помогает нам решать обратные задачи, можем сыграть в следующую игру. У меня есть три игральные кости, две из которых – обычные кубики с числами от одного до шести, а третья – либо с тройками, либо с нулями на всех гранях. Втайне от вас я одновременно брошу все три кости и назову общий итог. Каждый раз я могу использовать один кубик с подвохом – тот, на котором всегда выпадает ноль, или тот, на котором всегда выпадает тройка. Например, при первом броске я могу выбросить два, четыре и ноль (на третьем кубике), что в сумме составит шесть. Ваша задача: основываясь только на общем результате, сделать наилучшее предположение о том, какой кубик с подвохом я использовал – со всеми тройками или со всеми нулями[17].

В этой игре ноль или тройка на кубике с подвохом соответствуют «скрытым» состояниям мира: ракетам в дилемме Петрова и включенному свету в случае с нейронами зрительной коры. Тем или иным образом нам нужно использовать полученную искаженную информацию – сумму значений всех трех игральных костей, – чтобы определить скрытое условие.

Иногда это легко. Если я скажу, что общая сумма четыре или меньше, то вы поймете, что, раз значение такое маленькое, на третьем кубике должен был выпасть ноль. Если общий результат превышает 12 (две шестерки плюс число больше нуля), то вы точно знаете, что на третьем кубике выпала тройка. Но что насчет значений между этими крайностями? Если общий результат равен шести или восьми? Это сложнее.

Один из способов решения этой задачи – метод проб и ошибок. Мы можем много раз бросить кости, записать общий результат и понаблюдать за истинным положением вещей: что на самом деле выпадает на третьем кубике при каждом броске. Первые несколько бросков в игре могут выглядеть следующим образом:

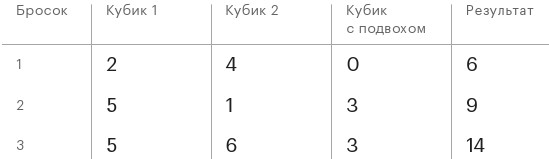
И так далее, еще много бросков. Более простой способ: представить эти данные в виде диаграммы, отображающей, сколько раз наблюдается определенное общее значение (скажем, шесть) и какой в этот момент использовался кубик (ноль или три). Кубики с подвохом можно обозначить определенными цветами: здесь я выбрал серый для кубика с нулями и белый для кубика с тройками.

После десяти бросков график может выглядеть следующим образом.

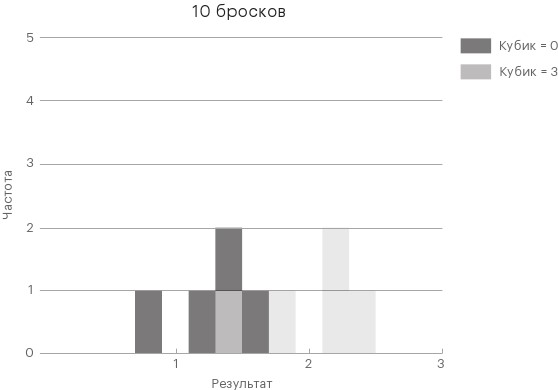
Не слишком информативно, и виден лишь разброс различных результатов, как и в нашей таблице. Но после пятидесяти бросков начинает проявляться закономерность.

А после тысячи картина становится весьма ясной.

Результаты, полученные в ходе нашего эксперимента, формируют две отчетливые вершины. Большинство бросков попадает в средний диапазон, а пики приходятся на семерку и десятку. Это логично. В среднем два обычных кубика дают в сумме около семи, и поэтому, добавив к этому числу ноль или три от кубика с подвохом, мы, как правило, получим семь или десять. То, что ранее говорила нам интуиция, подтвердилось: вы видите, что значение четыре или меньше получается только при броске кубика с нулем на всех гранях, а значение 13 и больше – только при использовании кубика с тройкой.

Теперь, вооружившись этими данными, давайте вернемся к нашей игре. Если я назову определенное общее значение, например десять, и попрошу вас угадать число на кубике с подвохом, что вы должны ответить? Согласно приведенному выше графику, вероятнее всего, в этом случае на кубике выпала тройка. Благодаря правилу Байеса мы знаем, что относительная высота белых и серых столбиков (при условии, что мы провели эксперимент достаточное число раз) отражает, насколько выше вероятность выпадения тройки по сравнению с нулем – в данном случае примерно в два раза. Согласно Байесу, оптимальное решение для этой игры – всегда называть наиболее вероятное значение кубика, то есть три, если общий результат девять или больше, и ноль – если восемь или меньше.

Только что мы набросали алгоритм для принятия решений на основе искаженной информации. Кубик с подвохом всегда маячит на заднем плане и вносит свой вклад в общий результат. Но его истинное значение заглушено помехами, создаваемыми двумя обычными кубиками. Точно так же Петров не мог определить наличие ракеты лишь по искаженному помехами сигналу радара. Наша игра является примером общего типа задач, связанных с принятием решений в условиях неопределенности, – их можно решить, применив правило Байеса.

В случае с судьбоносным решением Петрова набор потенциальных объяснений ситуации ограничен: либо это настоящая ракета, либо ложная тревога. Аналогичным образом, в нашей игре в кости есть только два объяснения: это кубик либо с тройками на гранях, либо с нулями. Но в большинстве ситуаций не только наша сенсорная система подвержена помехам, а еще существует целый диапазон потенциальных объяснений для поступающей информации. Представьте себе нарисованный круг около 20 сантиметров диаметром, который находится на расстоянии одного метра от вашего глаза. Отраженный от круга свет движется по прямой линии, проходит через хрусталик глаза и создает маленькое изображение (круг) на сетчатке. Поскольку изображение на сетчатке двухмерное, мозг может интерпретировать его как вызванное любым бесконечным числом кругов разного размера, расположенных на соответствующих расстояниях. Примерно такое же изображение на сетчатке вызвал бы круг диаметром 40 сантиметров, расположенный на расстоянии двух метров, или круг диаметром восемь метров на расстоянии 40 метров. Во многих случаях нам просто не хватает информации, чтобы определить, что мы видим.

В таких более сложных обратных задачах догадаться, в чем состоит лучшее объяснение, можно на основе дополнительной информации из других источников. К примеру, чтобы оценить фактический диаметр круга, мы можем использовать такие подсказки, как различия в изображении, получаемом разными глазами, разницу в текстуре, положении и оттенке близлежащих объектов и так далее.

Чтобы в реальном времени понять, как это происходит, взгляните на эти две картинки.

На изображении слева большинство людей видят группу выпуклых бугорков, приподнятых над поверхностью страницы. Изображение справа, напротив, выглядит как совокупность маленьких ямок или впадин. В чем же разница?

Иллюзия возникает из-за того, что ваш мозг решает обратную задачу. На самом деле левая и правая картинки – одно и то же изображение, развернутое на 180 градусов (можете перевернуть книгу и проверить!). Разными они кажутся, поскольку наша зрительная система привыкла, что свет падает сверху – источник света, заливающего окружающее пространство, обычно располагается где-то у нас над головой. В свою очередь, освещение снизу вверх – например, свет костра на склоне скалы или лучи прожекторов, направленные на верхушку собора, – статистически встречается реже. Когда мы смотрим на эти две картинки, наш мозг интерпретирует светлые части левого изображения как свет, падающий на выпуклые бугорки, а темные части правого изображения – как тени, создаваемые ямками, несмотря на то что обе картинки составлены из одного и того же исходного материала.

Другая поразительная иллюзия – изображение, созданное ученым Эдвардом Адельсоном.

Шахматная доска Адельсона

Клетки, обозначенные на левом рисунке буквами A и B, на самом деле окрашены в идентичный оттенок серого; они имеют одинаковую яркость. Клетка B кажется светлее, поскольку ваш мозг «знает», что она расположена в тени: чтобы воспроизвести для глаза тот же уровень освещенности, что и у клетки A, которая целиком находится на свету, она должна быть светлее изначально. Эквивалентность клеток A и B легко можно оценить, соединив их – как на правом рисунке. Подсказка, которую дает этот дополнительный мостик, перекрывает фактор тени в интерпретации мозгом изображения (чтобы убедиться, что левое и правое изображения одинаковы, попробуйте закрыть их нижнюю половину листом бумаги).

Получается, что на самом деле эти удивительные иллюзии – вовсе не иллюзии. Одну интерпретацию изображения дает научная аппаратура – показатели, выдаваемые измерителями освещенности и компьютерными мониторами. Другую – наши зрительные системы, настроенные на обнаружение закономерностей, таких как тени или свет, падающий сверху вниз. Эти закономерности помогают нашим системам выстраивать действенные модели мира. В реальном мире, где есть свет, тени и полутени, эти модели обычно оказываются верными. Многие оптические иллюзии хитроумным способом воздействуют на работу системы, искусно настроенной на получение перцептивных выводов[18]. Кроме того, как мы узнаем из следующего раздела, некоторые принципы устройства мозга согласуются с тем, как эта система в массовых масштабах решает обратные задачи.

Построение моделей мира

Зрительная система – одна из наиболее изученных частей мозга человека и обезьян. Различные области задней части мозга обрабатывают разные аспекты визуального сигнала. Чем выше их цифровое обозначение, тем более продвинутой стадии обработки изображения они соответствуют. Области V1 и V2 извлекают информацию о направлении линий и формах, V4 – о цвете, а V5 – о движении объектов. На выходе из областей V мы попадаем в русло вентрального зрительного потока, задача которого – собрать все части информации воедино и идентифицировать цельные объекты, такие как лица, тела, столы и стулья. Параллельно области мозга, входящие в дорсальный зрительный поток, отслеживают, где располагаются и как перемещаются объекты[19].

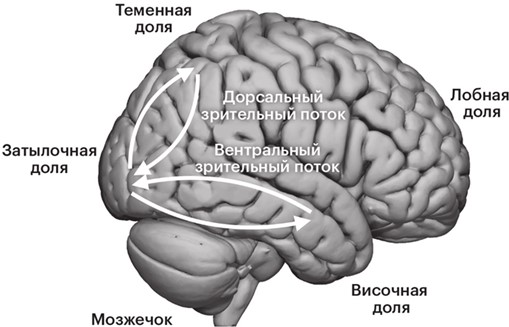
Правое полушарие мозга человека. Отмечено расположение четырех долей головного мозга, мозжечка и ключевых зрительных путей

В начале вентрального зрительного потока отдельные клетки мозга кодируют лишь небольшую часть внешнего мира – например, участок в нижнем левом углу нашего поля зрения. Но по мере продвижения вверх по иерархической структуре клетки, подобно отдаляющейся камере, начинают расширять свой фокус. В конце концов достигается высшая точка иерархии, в которой уже не столь важно, где отображается стимул. Гораздо большую роль играет, что он воссоздает: лицо, дом, кошку, собаку и так далее. Объектив максимально отдален, и информация об идентичности объекта представлена независимо от его расположения.

Однако крайне важно, что информация в зрительной системе не течет в одном направлении. Долгое время преобладало мнение, согласно которому обработка информации в мозге является системой прямого регулирования: она получает информацию из внешнего мира, обрабатывает ее тайными, хитроумными способами, а затем выдает команды, заставляющие нас ходить и говорить. Сейчас такая модель («вход – выход») вытеснена множеством данных, которые в нее не вписываются. В зрительной системе, например, существует столько же, если не больше, связей, направленных в противоположную сторону. Они так и называются – обратная связь, или «сверху вниз». Информация распространяется как вперед, так и назад; постоянные циклы нейронной активности поставляют данные как с нижних уровней иерархии на верхние, так и в обратном направлении. Такой способ рассмотрения механизмов сознания известен как предиктивная обработка. Это радикально иное понимание работы мозга, хотя оно имеет уже продолжительную интеллектуальную историю, о которой свидетельствует обширная библиография в примечаниях[20].

Архитектура предиктивной обработки особенно хорошо подходит для решения обратных задач. Вместо пассивного получения информации мозг может использовать связи «сверху вниз», для того чтобы активно строить наше восприятие внешнего мира и придавать форму тому, что мы видим, слышим, думаем и чувствуем. Более высокие уровни иерархии предоставляют информацию о том, с чем мы можем столкнуться в той или иной ситуации, а также о диапазоне гипотез, которые мы способны принять. Например, вы знаете, что у вашего друга есть лабрадор, и поэтому ожидаете увидеть собаку, когда входите в его дом, но не знаете, где именно в вашем зрительном поле она появится. Эта предварительная высокоуровневая информация – пространственно-инвариантное понятие «собака» – обеспечивает соответствующим контекстом более низкие уровни зрительной системы, помогая им легко интерпретировать размытое пятно в форме собаки, устремляющееся к вам, когда вы открываете дверь.

Степень, до которой наши системы восприятия должны полагаться на такие закономерности, в свою очередь, зависит от того, насколько мы сомневаемся в информации, поступающей от наших органов чувств. Вспомните дилемму Петрова. Если бы он был уверен в безупречности и безошибочности технологии обнаружения ракет, то в меньшей степени был бы готов усомниться в том, что говорила ему система. Стоит ли нам корректировать свои убеждения при получении новых данных, зависит от того, насколько надежной мы считаем эту информацию.

В действительности байесовские версии прогностической обработки говорят нам о том, что стоит комбинировать различные источники информации (наши предварительные убеждения и данные, поступающие через органы чувств) обратно пропорционально нашей неуверенности в них. Можно представить этот процесс как помещение теста для пирога в гибкую форму для выпечки. Форма – это наши предварительные предположения о мире. Тесто же представляет собой сенсорную информацию – световые и звуковые волны, улавливаемые глазами и ушами. Если поступающие данные точны или информативны, то тесто будет густым или почти твердым и на него почти не повлияет форма для выпечки. Если же, напротив, данные менее точны, то тесто будет более жидким и конечный продукт примет соответствующие очертания.

К примеру, глаза предоставляют более точную информацию о местонахождении объектов, нежели слух. Это означает, что зрение может изолировать предполагаемый источник звука, исказив наше восприятие его местоположения. Этим умело пользуются чревовещатели, способные «передавать» свой голос марионетке, которую они держат на расстоянии вытянутой руки. Истинное мастерство чревовещания заключается в умении говорить, не шевеля губами. Если добиться этого, мозг зрителей сделает все остальное, соотнеся звук с его следующим наиболее вероятным источником – говорящей куклой[21].

Таким образом, вполне логично, что отслеживание неопределенности – неотъемлемая часть того, как мозг обрабатывает сенсорную информацию. Наблюдения за клетками зрительной коры головного мозга показывают, как это может происходить. Хорошо известно, что движущиеся объекты, такие как машущая рука или прыгающий мяч, активируют нейроны в области мозга обезьян, известной как MT (аналог человеческой V5). Но клетки в MT активируются не при любом направлении движения. Некоторые из клеток больше реагируют на объекты, движущиеся влево, другие – вверх, вниз и во всех других направлениях. Когда частота возбуждения клеток МТ фиксируется в результате многократных воспроизведений различных направлений движения, формируется распределение, подобное тому, что мы наблюдали в игре в кости. В каждый отдельно взятый момент времени эти популяции клеток МТ можно считать сигнализирующими о неопределенности в отношении конкретного направления движения, аналогично тому, как искаженное общее значение игральных костей сигнализирует о вероятности выпадения ноля или тройки[22].

Неопределенность крайне важна и для оценки состояния нашего собственного тела. Информация о том, где в пространстве располагаются конечности, как быстро бьется сердце или какова интенсивность болевого стимула, поставляется в череп сенсорными нейронами. С точки зрения мозга разница между электрическими импульсами, проходящими по зрительному нерву, и нейронными сигналами, поступающими из кишечника, сердца, мышц или суставов, весьма незначительна. Все это – сигналы, сообщающие о том, что может происходить за пределами черепа, и искаженные иллюзиями вроде описанных выше оптических. В одном известном эксперименте поглаживание резиновой руки синхронно с настоящей (скрытой) рукой испытуемого убеждало его, что резиновая рука – его собственная.

В свою очередь, иллюзия обладания новой резиновой рукой приводила к ослаблению нейронных сигналов, посылаемых мозгом настоящей руке. Подобно тому как кукла перехватывает голос чревовещателя, синхронность наблюдений за резиновой рукой и ощущений при поглаживании уменьшает чувство обладания настоящей рукой[23].

Используем неопределенность, чтобы сомневаться

Конечно, никто не говорит, что каждый раз, познавая мир вокруг, мы специально прибегаем к уравнениям Байеса. Напротив, механизмы, используемые мозгом для решения обратных задач, срабатывают сами по себе – немецкий физик Герман фон Гельмгольц назвал это процессом «бессознательных умозаключений». Мозг быстро, буквально мгновенно оценивает влияние света и тени на впадины, выпуклости и шахматные доски, изображения которых мы видели на предыдущих страницах.

Аналогичным образом мы воссоздаем лицо близкого друга, вкус хорошего вина и запах свежеиспеченного хлеба, комбинируя предварительные предположения и информацию от органов чувств; тщательно взвешивая их с учетом соответствующих неопределенностей. Нейробиолог Анил Сет называет наше восприятие мира «контролируемой галлюцинацией» – наилучшим предположением о том, что на самом деле есть.

Очевидно, что оценка неопределенности, характеризующей те или иные источники информации, – основа нашего восприятия мира. Но изобретательные решения обратных задач дают замечательный побочный эффект. Оценивая неопределенность для того, чтобы воспринимать мир, мы обретаем способность сомневаться в том, что воспринимаем. Чтобы увидеть, как неопределенность с легкостью превращается в сомнение, давайте снова обратимся к игре в кости. Чем ближе общее значение к 15 или к нулю, тем больше мы уверены, что на кубике с подвохом выпала соответственно тройка или ноль. Но в средней части графика, где серые и белые столбики равны по высоте (общие значения равняются семи и восьми), доказательств недостаточно для любого из вариантов. Если я спрошу вас, насколько вы уверены в своем ответе, будет разумно, если вы усомнитесь, когда речь пойдет о значениях семь и восемь, но будете более уверены в случае меньших или бóльших результатов. Другими словами, мы знаем, что, скорее всего, знаем ответ, если неопределенность низкая, и знаем, что, скорее всего, не знаем ответ, когда неопределенность высокая.

Правило Байеса дает математическую основу для размышлений об этих оценках неопределенности, которые называют еще решениями второго типа, поскольку они касаются точности других решений – в отличие от решений первого типа, которые касаются окружающего мира. Согласно теореме Байеса, нам следует больше сомневаться, когда дело касается ответов, приходящихся на центр графика, поскольку именно они чаще всего приводят к ошибкам и с наименьшей вероятностью оказываются правильными. И напротив, по мере приближения к краям распределения вероятность правильного ответа возрастает. Используя неопределенность, присущую решению обратных задач, мы в качестве бонуса достигаем рудиментарной формы метапознания – и никаких дополнительных механизмов для этого не требуется[24].

Поскольку отслеживание неопределенности играет основополагающую роль в том, как мозг воспринимает мир, неудивительно, что эта форма метапознания доступна множеству животных. Один из первых – и наиболее изобретательных – экспериментов по изучению метапознания у животных был проведен психологом Дэвидом Смитом, работавшим с бутылконосым дельфином по имени Натуа. Смит обучил Натуа нажимать на разные рычаги в аквариуме в зависимости от частоты слышимого им звука. Низкочастотный звук варьировался от очень низкого до относительно высокого, почти высокочастотного. Таким образом, как и в нашей игре в кости, создавалась зона неопределенности, когда сложно было понять, какой же ответ правильный[25].

Когда Натуа научился справляться с этим заданием, в аквариум добавили третий рычаг, нажав на который можно было пропустить текущий звук и сразу перейти к следующему – дельфиний аналог пропуска вопроса в тесте. Смит рассудил, что если Натуа, будучи не уверен в ответе, откажется принимать решение, вместо того чтобы угадывать, то сможет добиться более высокой общей точности. Именно это Смит и обнаружил. Результаты показали, что чаще всего Натуа нажимал на третий рычаг, когда звук был пограничным. Как пишет Смит, «в случае неуверенности дельфин явно сомневался и колебался между двумя возможными ответами, но когда был уверен, то так устремлялся к выбранному ответу, что разгонял волну и заливал аппаратуру исследователей»[26].

Макаки – обезьяны, которые встречаются по всей Азии (и любят воровать еду у туристов в храмах и святилищах), – тоже легко обучаются отслеживать свою неуверенность в похожих ситуациях. В одном эксперименте макак обучали определять самую большую фигуру на экране компьютера. Затем им нужно было выбрать между двумя иконками. Первая иконка означала рискованную ставку (три кусочка еды в случае правильного ответа, за ошибку еду убирали), в то время как другой, безопасный вариант гарантировал один кусочек еды – обезьяний вариант игры «Кто хочет стать миллионером?». Обезьяны чаще выбирали рискованный вариант, когда отвечали правильно, что красноречиво свидетельствует о метапознании. Что впечатляет еще больше, они сразу же, без дополнительного обучения, справились с оценкой уверенности в своих ответах в другом тесте на память, исключив предположение, что они просто учатся ассоциировать определенные стимулы с ответами разной степени уверенности. С помощью похожего задания исследователи из лаборатории Адама Кепекса, расположенной в Колд-Спринг-Харбор в Нью-Йорке, продемонстрировали, что крысы тоже могут оценивать свою правоту насчет того, какой из двух запахов преобладает в смешанном аромате. Есть даже некоторые свидетельства, что птицы, как и обезьяны, способны переносить свои наработанные метакогнитивные навыки из одного испытания в другое[27].

Если чувствительность к неопределенности – это фундаментальное свойство работы мозга, то вполне логично, что у людей этот первый кирпичик метапознания можно обнаружить в самом раннем возрасте. Вдохновившись тестами Смита, Луиза Гупиль и Сид Куидер из Высшей нормальной школы в Париже решили исследовать, как неопределенность своих решений отслеживают 18‐месячные младенцы. Малышам, сидящим на коленях у матерей, демонстрировали заманчивую игрушку и давали поиграть с ней, возбуждая интерес. Затем им показывали, как игрушку прячут в одну из двух коробок. Наконец после небольшой паузы малышам разрешалось заглянуть в одну из коробок, чтобы достать игрушку.