comparative linguistics - читать онлайн

2.1. PAI Method

2.1.1. PAI method background

A. P. Volodin pointed on the fact that all languages can be subdivided into two sets by the parameter of presence/absence of prefixation: one group has prefixation and the other has not (Volodin 1997: 9).

The first set was conventionally named set of “American type” linear model of word form7.

According to Volodin American type linear model of word form is the following:

(p) + (r) + R + (s).

The second one was conventionally named set of “Altaiс type” linear model of word form8.

According to Volodin it is the following:

(r) + R + (s)

(p – prefix, s – suffix, R – main root, r – incorporated root; brackets mean that corresponding element can be absent or can be represented several times inside a particular form).

Volodin supposed that there was a border between two sets and that languages belonging to the same set demonstrate certain structural similarities. Also he supposed that typological similarities could probably tell us something about possible routes of ethnic migrations.

2.1.2. PAI hypothesis development

Having got Volodin’s notion about two types of linear model of word form, I for quite a long time thought that there was a pretty strict water parting between languages that have prefixation and those that have not. For instance, I seriously thought that Japanese had no prefixes and tried to consider all prefixes of Japanese as variations of certain roots, i.e. as components of compounds; until one day I finally realized that so called “variations of roots” actually could never be placed in nuclear position and so they all should be considered as true prefixes, so strict dichotomy was broken and I had to elaborate new theory.

As far as any language actually has some ability to make prefixation so there is no strict border between languages with prefixation and languages without prefixation and we should give up ideas of strict subdivision of all existing languages into two sets that have no intersection.

Hence thereupon, linear model of word forms have the following structures:

(P) + (R) + r + (s) – linear model of word form of American type;

(p) + (r) + r + (S) – linear model of word form of Altaic type.

Capital letters are markers of positions that are used more than positions marked by small letters.

Thereby, there is no principal structural difference between languages of American type and Altaic type, difference is in degree of manifestation of certain parameters and so, in order to our conclusion will not be speculative, we should speak about degree of prefixation producing ability / prefixation ability degree / prefixation ability index, i.e.: of certain measure of prefixation.

I suppose that each language has its own ability to produce prefixation and that this ability doesn’t change seriously during all stages of its history.

Also I suppose that prefixation ability demonstrates itself in any circumstances, i.e.: it is manifested by any means: by means of original morphemes existing in a certain language or by borrowed morphemes.

If a language has certain prefixation ability it is shown anyway. That’s why I don’t make difference between original and borrowed affixes.

Also for current consideration is not principal whether this or that affix is derivative or relative: if we take into account relative affixes only, then, for instance, Japanese is a language without prefixes.

That’s why we should define prefixes not by its derivative or by its relative role but by its positions inside word form, prefix is any morpheme that meets the following requirements:

1) it can be placed only left from nuclear position;

2) it never can be placed upon nuclear position;

3) between this morpheme and nuclear can’t be placed any meaningful morpheme with its clitics (i.e.: between nuclear root and prefix can’t be placed a meaningful morpheme with its auxiliary morphemes).

I am specially to note that there are no so called semi-prefixes. If a morpheme can be placed in nuclear position it is meaningful morpheme and any combinations with it should be considered as compounds.

Thus can be resumed the following:

1) Each language has its own ability to produce prefixation and this ability doesn’t change seriously during all stages of its history.

2) Prefixation ability is manifested by any means: by means of original morphemes existing in a certain language or by borrowed morphemes. That’s why the method doesn’t suppose distinction between original and loaned affixes.

3) Genetically related languages are supposed to have rather close values of Prefixation Ability Index.

2.1.3. PAI calculation algorithm

How Prefixation Ability Index (here and further in this text abbreviation PAI is used) can be measured?

Value of PAI is portion of prefixes among affixes of a language.

Hence, in order to estimate portion/percentage of prefixes of a certain language we should do the following:

1) Count total number of prefixes;

2) Count total number of affixes;

3) Calculate the ratio of total number of prefixes to the total number of affixes.

Why is it important to count total number of prefixes and then calculate the ratio to the total number of affixes but not to estimate PAI by frequency of prefix forms in a random text?

A certain language can have quite high value of PAI but in a particular text word forms with prefixes can be of low frequency. Our task is to estimate portion of prefixes in grammar but not portion of prefix forms in a random text. Prefixes/World index estimated by Greenberg was exactly that estimation of prefix forms frequency in a text (Greenberg 1960).

Of course, that index also can give some general notion of prefixation ability of a language, though it is extremely rough and inaccurate since in a randomly chosen text can be very little amount of words with prefixes: the longer text is the more precision is the conclusion but anyway error of such estimation still remains very high; while when we count all exiting affixes of a certain language potential error is extremely low and even if we occasionally forget some affixes it doesn’t influence seriously on our results.

Moreover I am to note that despite Greenberg made great work on the field of typology he didn’t actually use those results in his research; he was an adept of megalocomparison and made his conclusions basing on “mass comparison” of lexis but not on structural correlations; his interest in typology was a “glass beads game” and was separated from his actual field of studies.

To those who think, that it’s impossible to estimate number of morphemes since living language always changes, I am to tell that living language doesn’t invent new morphemes every day, especially auxiliary morphemes. The fact that learning a language we can use descriptions of its grammar written some decades ago is the best proof that grammar is a very conservative level of any language.

Hence, we can estimate total number of affixes of a living language as far as we can get its description where all stable forms are represented. And there is no need to care of what can be in a certain language in future, i.e.: we consider current stage of living language and don’t care of possible future stages since they simply don’t exist yet.

As for possibility of count, I am to tell that even set of words is countable set while set of morphemes and especially auxiliary morphemes is not just countable set but also is finite set.

2.1.4. PAI method testing: from a hypothesis toward a theory

In order to test PAI hypothesis I paid attention to some languages of firmly assembled stocks: Austronesian, Indo-European and Afroasiatic.

2.1.4.1. PAI of languages of Austronesian stock

Polynesian group

Eastern Polynesian Subgroup

Hawaiian 0.82 (calculated after Krupa 1979)

Maori 0.88 (calculated fater Krupa 1967)

Tahitian 0.66 (calculated after Arakin 1981)

Samoan-Tokelauan subgroup

Samoan 0.5 (calculated after Arakin 1973)

Tongic subgroup

Niuean 0.8 (calculated after Polinskaya 1995)

Tongan 0.78 (calculated after Fell 1918)

Philippine group

South Mindanao subgroup

T’boli 0.72 (calculated after Porter 1977)

Northern Luzon subgroup

Pangasinan 0.6 (calculated after Rayner 1923)

Malayo-Sumbawan group

Malay subgroup

Indonesian 0.53 (calculated after Ogloblin 2008)

Pic. 2. Map representing location of Austronesian languages mentioned in current chapter: languages are marked by red, place names are maked by black.

Chamic subgroup

Cham 0.6 (calculated after Aymonier 1889; Alieva, Bùi 1999)

Formosan group

Bunun 0.8 (calculated after De Busser 2009)

Eastern Barito group

Malagasy 0.74 (calculated after Arakin 1963)

2.1.4.2. PAI of languages Indo-European stock

German group

Dutch 0.49 (calculated after Donaldson 1997)

German 0.51 (calculated after Donaldson 2007)

English 0.61 (calculated after Barhkhudarov et al. 2000)

Icelandic 0.63 (calculated after Einarsson 1949)

Slavonic group

Czech 0.52 (calculated after Harkins 1952)

Polish 0.57 (calculated after Swan 2002)

Celtic group

Irish 0.67 (McGonage 2005)

Welsh 0.35 (calculated after King 2015)

Roman group

Latin 0.26 (calculated after Bennet 1913)

Spanish 0.34 (calculated after Kattán-Ibarra, Pountain 2003)

2.1.4.3. PAI of languages of Afroasiatic stock

Semitic group

Central Semitic subgroup

Arabic (Classical) 0.26 (calculated after Yushmanov 2008)

Phoenician 0.26 (calculated after Shiftman 2010)

Eastern Semitic subgroup

Akkadian (Old Babylonian dialect) 0.2 (calculated after Kaplan 2006)

Egypt group

Coptic (Sahidic dialect) 0.87 (calculated after Elanskaya 2010)

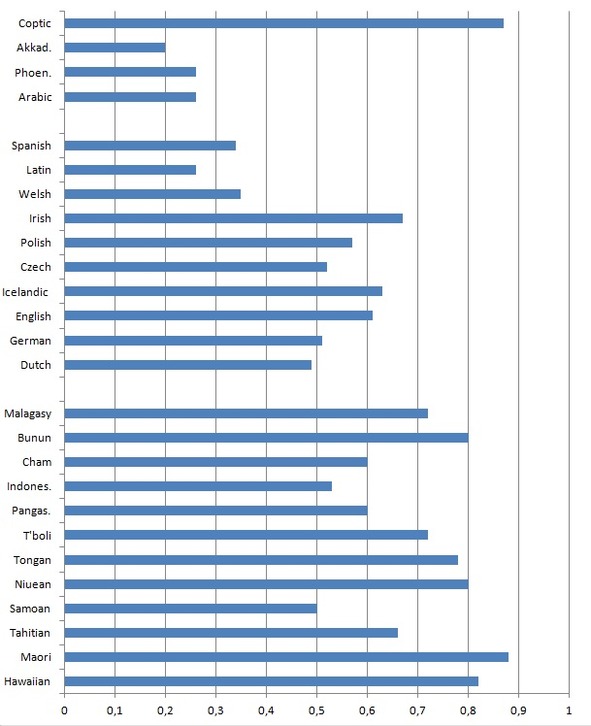
Pic. 3. Diagram representing PAI values of some firmly assembled stocks

2.1.5. PAI of a group/stock

PAI of a group or a stock can be calculated as arithmetical mean and it’s quite precise for rough estimation.

One can probably say that just arithmetic mean is quite rough estimation and in order to estimate PAI in a more precise way it would be better to take values of PAI of particular languages with coefficients that show proximity of particular languages to the ancestor language of the stock. Coefficient of proximity is degree of correlation of grammar systems.

Let’s test this hypothesis and see whether it so.

For instance, in the case of Austronesian it would be somehow like the following:

Malagasy^PAN9 ≈ 0.5;

Bunun^PAN ≈ 0.8;

Philippine group^PAN ≈ 0.7;

Indonesian^PAN ≈ 0.6;

Cham^PAN ≈ 0.4;

Polynesian languages^PAN ≈ 0.5.

Indexes show degree of proximity of languages (grammatical systems). In current case these indexes are not results of any calculations but just approximate speculative estimation of degrees of proximity of modern Austronesian languages with Proto-Austronesian; it is supposed that Formosan languages and so called languages of Philippines type are the closest relatives of PAN among modern Austronesian.

If we take each particular PAI value with corresponding coefficient of proximity we get that PAI of Austronesian is about 0.44.

If we take just arithmetical mean without proximity coefficients we get 0.6.

0.6 is obviously closer to real values of PAI of Austronesian languages than 0.44. Hence thereby it’s possible to state that just arithmetical mean is completely sufficient way to calculate PAI of a group/stock while PAI calculated with use of proximity coefficients gives results that differ seriously from reality.

2.1.6. PAI in diachrony

It can be supposed that PAI doesn’t change much in diachrony.

PAI of Late Classical Chinese is 0.5 (calculated after Pulleyblank 1995).

PAI of Contemporary Mandarin is 0.5. (calculated after Ross, Sheng Ma 2006).

PAI of Early Old Japanese is 0.13 (calculated after Syromyatnikov 2002).

PAI of contemporary Japanese is 0.13 (calculated after Lavrent’yev 2002).

Probably it should be also tested on other examples but even on the material of these examples we can see that PAI of a language is same in different stages of its history.

2.1.7. Summary of PAI method

One can probably say that Coptic has broken our hypothesis, but actually PAI just has shown us that group of Coptic language and Semitic group diverged very long ago, probably in Neolithic epoch yet.

However, the tests have shown that values of PAI of related languages are actually rather close, i.e.: they do not differ more than fourfold (pic. 3).

Thus, it is possible to say that PAI is something alike safety valve of comparative linguistics: if its values don’t differ more than fourfold then PAI has no distinction ability and actually there are no obstacles for further search for potential genetic relationship; but if values of PAI differ fourfold and more, then should be found absolutely ferroconcrete proves of genetic relationship.

Also I am specially to note that PAI method doesn’t require estimation of measurement error as far as PAI allows fourfold gap of values.

2.2. Why is it possible to prove that languages are not related?

2.2.1. Root of problem is changing of concepts

One can probably say that it is impossible to prove unrelatedness of two languages so I am to make some explanation on why it is possible.

In contemporary comparative linguistics there is a weird presupposition that it is impossible to prove that certain languages are not genetically related. As I can understand this point of view was inspired by Greenberg as well as some other obscurantist ideas of contemporary historical linguistics. It seems quite weird that it is possible to prove relatedness but it is not possible to prove unrelatedness. Let’s check whether it is so.

First of all, I am to note that statement about impossibility of proving unrelatedness is actually sophism based on changing of concepts, i.e.: when they speak about proves of relatedness then relatedness means “to belong to the same stock” and it is regular and normal meaning of the concept of relatedness in linguistics; however, when they speak about unrelatedness then meaning of relatedness suddenly changes: they start to suppose that actually all existing languages are related since they are supposed to be derivates of same proto-language that existed in a very distant epoch in past and due to this fact we can’t prove unrelatedness but can just state that a language doesn’t belong to a stock.

2.2.2. Concepts of relatedness and unrelatedness from the point of view of other sciences

In order to clear the meaning of the concept of relatedness it’s useful to pay some attention to other sciences where this concept also is used. If we take a look at, for instance: biology, physics or technical sciences we can see that many items are distributed by classes/classified despite they obviously have common origin; and considering them it is completely normal to speak about relatedness and unrelatedness. All being have common origin and so they all are relatives in a very deep level but this fact doesn’t mean they cannot be classified into kingdoms, phylums, classes, orders, suborders, families, subfamilies; the fact that ant, bear, pine tree, whale, sparrow have common ancestor doesn’t mean it is impossible to distinguish bear from whale and whale from pine tree.

However, as far as languages aren’t self replicating systems like biological systems and are closer to artifacts so any parallels between biological systems and language always should be made with certain degree of awareness since they are more allegories than analogies while correlations between languages and some artificial items are more precise, for instance: all existing cars are derivates of steam engine that existed in the middle of 19^th century, but it doesn’t mean we can’t classify cars/engines and speak of relatedness and unrelatedness of certain types.

These examples evidently show us the following:

1) When they say about an item that is related with another it means “they both belong to the same class”.

2) It is possible to speak about relatedness and unrelatedness of certain items even though all classes of them have common origin.

2.2.3. Concepts of relatedness and unrelatedness from point of view of set theory and abstract algebra

Concept of relatedness is actually equivalence relation since it meets necessary and sufficient requirements for a binary relation to be considered as equivalence relation:

1) Reflexivety: a ~ a: a is related with a;

2) Symmetry: if a ~ b then b ~ a: if a is related with b then b is related with a;

3) Transitivity: if a ~ b and b ~ c then a ~ c: if a is related with b and b is related with c then a is related with c.

If an equivalence relation is defined on a set then it necessarily supposes grouping of elements of the set into equivalence classes and these classes aren’t intersected (Hrbacek, Jech: 1999).

2.2.4. Particular conclusions on the concepts of relatedness and unrelatedness for linguistics

When it is said that certain languages are genetically related (or simply related) it means that these languages belong to the same stock or even to the same group.

Taking into the consideration what has been said in 2.2.2 we should keep in mind that in the case of languages there are actually no positive evidences that all languages existing nowadays originated from the same ancestor, i.e.: monogenesis is still an unproved hypothesis, though anyway even if all languages can be reduced to the same proto-language that existed in a very distant past it doesn’t mean yet we can’t speak of their relatedness/unrelatedness.

Then, taking into consideration what has been said in 2.2.3 we can say the following:

The set of languages existing nowadays on the planet is rather well described: we know that there are about 7102 languages and about 151 stocks and 83 isolated languages (Ethnologue: 2015), so we can speak about 234 stocks; and we hardly can expect discovering of some new unknown languages. Thus, we can say that we have rather complete image of set of languages and that there are about 234 classes of equivalence/relatedness.

If we take an X stock, we obviously can show many languages which don’t belong to the stock, i.e.: languages which are not related with language x (a random language of X stock), for example: in the case of Indo-European stock there are many languages which are not related with English: Arabic, Basque, Finnish, Georgian, Turkish, Chinese, Japanese, Hawaiian, Eskimo, Quechua and so on. In the case of Sino-Tibetan stock there are many languages which aren’t related with Chinese: Arabic, English, Eskimo, Finnish, Japanese, Turkish, Vietnamese and so on.

Thus, we can conclude the following:

1) Relatedness means “language belongs to a stock” unrelatedness means “language doesn’t belong to a stock”.

2) If set of 234 classes/stocks has been set up then it obviously supposes that there should be a possibility of classification, i.e.: we can say whether a language belongs to a stock; moreover, we always can show some languages which don’t belong to the stock. If possibility to prove unrelatedness is denied then we actually can’t establish scopes of stocks and can’t distinguish one stock from another; then even a single stock hardly could have been assembled.

3) Any two randomly chosen languages can be related or not related, i.e.: there can be no “third variant” since relatedness/unrelatedness supposes the existence of classes which don’t intersect. If a language of X stock is related to a language of Y stock it means that these stocks are related.

4) Possible objection can be the following: one can probably say that it is impossible to make precise conclusions in linguistics. Actually, I don’t think someone can seriously say this, however, if someone would speak out something like this I can only point on the fact that very long ago people thought that precise conclusions are impossible in physics. Possibility of precise estimations and precise conclusions depends on scholars’ will and on scholars’ intellectual courage only, but not on material itself; any material can be represented as item that can’t be formalized, and many items have already been successfully formalized.

2.2.5. An important consequence: transitivity of relatendness/unrelatedness

If we have proven unrelatedness of an x language belonging to X stock with y language that belongs to Y stock then, due to transitivity of unrelatedness, it means that x is not related with the whole Y stock.

2.3. Applying PAI method to some unsettled hypotheses

2.3.1. PAI against Nostratic hypothesis

Basing on comparison of lexis adepts of Nostratic hypothesis state that Indo-European stock, Kartvelian stock, Uralic stock and Turkic stock are relatives. Let’s see and test whether, for instance, Indo-European and Turkic stocks could be relatives.

PAI of Indo-European is about 0.5 (calculated after data represented in 2.1.4.2);

PAI of Turkic stock is about 0.012 (calculated after Yazyki mira. Tyurkskiye yazyki 1996).

Values of PAI differ more than tenfolds so these stocks evidently can’t be genetically related.

2.3.2. Whether Ainu belongs to Altaic stock?

Having compared some randomly chosen lexemes, Patrie states that Ainu is a relative of Japanese and Korean and thus belongs to Altaic stock (Patrie 1982).

Whether Japanese and Korean are part of Altaic stock is still a discussed issue and even relationship of Japanese and Korean is still actually questionable. However, let’s accept Patrie’s proposition and let’s look at PAI of these languages.

PAI of Ainu is 0.75 (calculated after Tamura 2000);

PAI of Japanese is 0.13 (see 2.1.6);

PAI of Korean is 0.13 (calculated after Mazur 2004).

Values of PAI of Ainu and Japanese/Ainu and Korean differ sixfold.

In the case of Coptic language and Semitic group values of PAI differ fourfold and if there were no firm structural evidences relationship of Coptic language and Semitic group would be very problematic.

In the case of Ainu and Altaic stock serious difference of PAI values is obviously proof of absence of relatedness. Ainu and Korean, Ainu and Japanese are completely unrelated like, for instance, Spanish and Basque.

Moreover, we should keep in mind that Japanese and Korean have probably the highest values of PAI among languages of Altai stock so if we compare Ainu with some “true” languages of Altaic stock the difference is much more striking.

And also the fact there is almost no structural correlation between Ainu and Japanese and between Ainu and Korean corroborates conclusion made with the use of PAI.

2.3.3. PAI suggests that Buyeo stock seems to be real

Japanese and Korean seem to be closer relatives than it has been thought usually, since their PAI values completely coincide (see 2.3.2). And this fact correlates well with their structural and material correlation.

Anyway after discovering closeness of PAI values proximity of grammar systems should be shown.

The question of Japanese and Korean relationship is considered in (5.2).

2.3.4. PAI against Mudrak’s hypotheses

Mudrak believes that such languages as: Ainu, Nivkh, Chukchi-Koryak, Itelmen and Eskimo-Aleut are genetically related (Mudrak 2013).

2.3.4.1. Whether Ainu and Nivkh could be relatives

According to Mudrak Ainu and Nivkh not just belong to that hypothetical stock but belong to same group inside the stock (pic. 4).

Pic. 4. Scheme representing genetic relationships of “Paleosiberian stock” languages accordingto Mudrak (source: [битая ссылка] http://polit.ru/article/2013/04/22/ps_mudrak_linguistics/ – accessed December 2015)

PAI of Nivkh is 0.07 (calculated after Gruzdeva 1997);

PAI of Ainu is 0.75.

Values differ more than tenfold.

Also grammars of Ainu and grammar of Nivkh show serious differences.

Hypothesis of Nivkh and Ainu relationship is same as for instance hypothesis of common ancestor of Estonian and Latvian spoken out by Nivkh or Ainu scientists (if Nivkh or Ainu would have scientists and European languages would be “indigenous languages”). It’s completely naïve and it’s based only on very perfunctory impression of some cultural similarities of Sakhalin Nivkh and Sakhalin Ainu.

2.3.4.2. Whether Ainu and Eskimo-Aleut could be relatives?

PAI of Aleut group and its relatives is zero (Golovko 1997: 115; Menovschikov 1997: 77). PAI of Ainu is 0.75. We have seen some well assembled groups and stocks and know how values of PAI can differ if languages really form a stock. As far as our current math, that we use to count values of PAI and estimate correlation of PAI values, doesn’t know division by zero so we can ascribe to the PAI of Aleut an obviously absurd value (for instance: 0.000001) in order to show the utmost absurdity of any attempts to represent Ainu and Aleut as languages belonging to the same stock.

Pic. 5. Diagram representing PAI values of languages that don’t form stocks.

2.3.4.3. Against term “Paleosiberian”

The term “Paleosiberian languages” was invented to designate isolated languages of Siberia and Far East; it doesn’t mean a hypothetical stock but it is just a set of genetically unrelated languages assembled by their geographic location. Now it would be better to avoid use of this term as far as it doesn’t help to analyse and discover but just inspires development of megalocomparative obscurantism.

It would be better to use term “isolated languages and stocks of Siberia and Far East” rather than to explain every time true meaning of term “Paleosiberian” since it looks much alike name of stock, it looks too mystic and/or intriguing for random amaterish people could properly understand its meaning.

2.3.5. Potential relatives of Ainu seem to be in South

2.3.5.1. Ainu and Austronesian

Murayama believed that Ainu could be a distant relative of Austronesian (Murayama 1993).

Despite naïve lexicostatistic approach the idea potentially can be rather realistic since PAI of Ainu is 0.75 and PAI of Austronesian stock is about 0.6.

2.3.5.2. Ainu and Mon-Khmer

Vovin tried to show that Ainu was a distant relative of Austroasiatic (Vovin 1993). As well as in the case of Murayama the idea isn’t completely off base since PAI of Khmer is 0.66 that correlates well with that of Ainu. However, I am to note that such researches in the field of linguistics should be correlated with data of other sciences.

2.3.6. Particular conclusion about PAI method

1. PAI is something alike safety valve of comparative linguistics: if its values don’t differ more than fourfold then there is absolutely no obstacles for further research about genetic relationship; if values differ fourfold and more then should be found absolutely ferroconcrete proves of genetic relationship; if values differ sevenfold – tenfold or even more then those languages belong to different stocks.

It is possible to say that PAI shows direction in which looking for potential relatives of certain language can be perspectives.

2. PAI can be helpful method in those areas where are many isolated languages/stocks: in North America, in Papua and in Africa.