Конспект к учебнику И.В.Савельева «Основы теоретической физики», т. 2 - читать онлайн

Глава

II

2.07.Основные постулаты квантовой механики (25)

Будем использовать Q вместо для операторов !!!

Первый постулат утверждает, что каждую физическую величину можно представить линейным оператором

Второй постулат квантовой механики гласит, что в результате измерения физической величины Q, представляемой оператором , может получаться лишь одно из собственных значений q_m оператора

Третий постулат квантовой механики утверждает, что при измерениях, осуществляемых над системой, находящейся в состоянии ψ, для определения значения величины Q, по функциям которой осуществлено разложение , вероятность получить значение q_m равна (при надлежащей нормировке функций) квадрату модуля коэффициента c_m

Qφ = f

линейный оператор:

Q(φ₁ + φ₂) = Q(φ₁) + Q(φ₂)

Q(cφ) = cQφ

QΣc_mφ_m = Σc_mQφ_m

пример:

∂Σc_mφ_m/∂x = Σc_m∂φ_m/∂x

собственные значения и собственные функции:

Qψ = qψ

q₁, q₂, … , q_m, …

ψ₁, ψ₂, … , ψ_m, …

ψ = Σc_mψ_m

Σ|c_m|² = Σc_m^*c_m = 1

∫ψ_m^*ψ_ndV = δ_mn

скалярное произведение функций:

<φ|ψ> ≡ ∫φ^*ψdV (1)

<φ|φ> = ∫φ^*φdV = ∫|φ|²dV

= ∫(aφ)^*ψdV = a^*∫φ^*ψdV = a^*<φ|ψ>

<φ|bψ> = ∫φ^*(bψ)dV = b∫φ^*ψdV = b<φ|ψ>

= a^*b<φ|ψ>

<φ|ψ>^* = (∫φ^*ψdV)^* = ∫ψ^*φdV = <ψ|φ>

<φ|ψ>^* = <ψ|φ> (2)

<φ|Qψ>^* = (∫φ^*QψdV)^* = ∫(Qψ)^*φdV =

<φ|Qψ>^* =

^* = (∫(Qφ)^*ψdV)^* = ∫ψ^*(Qφ)dV = <ψ|Qφ>

^* = <ψ|Qφ>

ψ = Σc_mψ_m

<ψ_n|ψ_m> = ∫ψ_n^*ψ_mdV = δ_nm

<ψ_n|ψ> = <ψ_n|Σc_mψ_m> = Σc_m<ψ_n|ψ_m> = Σc_mδ_nm = c_n

c_n = ∫ψ_n^*ψdV = <ψ_n|ψ> (3a)

c_n^* = (∫ψ_n^*ψdV)^* = ∫ψ^*ψ_ndV = <ψ|ψ_n>

c_n^* = ∫ψ^*ψ_ndV = <ψ|ψ_n> (3b)

= Σq_m|c_m|² = Σq_mc_m^*c_m = Σq_m(∫ψ^*ψ_mdV)c_m = Σ(∫ψ^*q_mψ_mdV)c_m =

= Σ(∫ψ^*Qψ_mdV)c_m = ∫ψ^*QΣc_mψ_mdV = ∫ψ^*QψdV

= ∫ψ^*QψdV = <ψ|Qψ> (4)

через скалярное произведение функций (наглядней):

= Σq_m|c_m|² = Σq_mc_m^*c_m = Σq_m<ψ|ψ_m>c_m = Σ<ψ|q_mψ_m>c_m =

= Σ<ψ|Qψ_m>c_m = <ψ|QΣc_mψ_m> = <ψ|Qψ>

Мы получили одну из важных формул квантовой механики. Она позволяет, зная пси-функцию состояния, находить среднее значение результатов измерений любой физической величины. Для этого нужно знать также вид оператора, соответствующего данной величине.

2.08.Линейные операторы(30)

комплексно сопряженный оператор:

(Qφ)^* = Q^*φ^* (5)

транспонированный оператор:

Q^T ≡ Q̃

<ψ|Qφ> =∫ψ^*Qφdq ≡ ∫φQ̃ψ^*dq = <φ^*|Q̃ψ^*>

<φ^*|Q̃ψ^*> ≡ <ψ|Qφ> (6a)

<φ|Q̃ψ> = <φ^**|Q̃ψ^**> = <ψ^*|Qφ^*> (6b)

<φ|Q^ТТψ> = <ψ^*|Q^Тφ^*> = <φ|Qψ>

Q^ТТ = Q (6c)

эрмитово сопряженный оператор:

+φ|ψ> ≡ <φ|Qψ> (7a)

<Ô⁺φ|ψ> = <φ|Qψ> =∫φ^*QψdV = ∫ψQ̃φ^*dV = ∫(Q̃^*φ)^*ψdV = *φ|ψ>

Q⁺ = Q̃^* (7b)

через скалярное произведение функций:

<φ|ψ>^* = <ψ|φ>

<φ|ψ>^* = (∫φ^*ψdV)^* = ∫φ^**ψ^*dV = < φ^*|ψ^*>

+φ|ψ> = <φ|Qψ> = <ψ^*|Q̃φ^*> = *|ψ^*>^* = <(Q̃φ^*)^*|ψ> = *φ|ψ>

Qψ_n = q_nψ_n <ψ_n|ψ_n> = 1

∫ψ_n^*Qψ_ndV = ∫ψ_n^*q_nψ_ndV = q_n∫ψ_n^*ψ_ndV = q_n

<ψ_n |Qψ_n> = <ψ_n |q_nψ_n> = q_n<ψ_n|ψ_n> = q_n

1) q_n = ∫ψ_n^*Qψ_ndV = <ψ_n |Qψ_n>

q_n^* = (∫ψ_n^*Qψ_ndV)^* = (∫ψ_nQ̃ψ_n^* dV)^* =∫ψ_n^*Q̃^*ψ_ndV = ∫ψ_n^*Q⁺ψ_ndV

q_n^* = <ψ_n|Qψ_n>^* = n|ψ_n> = <ψ_n|Q⁺ψ_n>

2) q_n^* = ∫ψ_n^*Q⁺ψ_ndV = <ψ_n|Q⁺ψ_n>

q_n = q_n^* ⇔ <ψ_n |Qψ_n> = <ψ_n|Q⁺ψ_n> ⇔ Q = Q⁺

короче:

q_n = q_n^*

< Q⁺ψ_n|ψ_n> = <ψ_n|Qψ_n> = q_n = q_n^*= <ψ_n|Qψ_n>^* = n|ψ_n>

Q⁺ = Q

Определение. Оператор, для которого выполняется условие Q = Q⁺, называется сопряженным или эрмитовым.

Итак, мы пришли к выводу, что физические величины, для которых собственные величины вещественны, должны изображаться самосопряженными (эрмитовыми) операторами Q, для которых справедливы соотношения

<φ|Qψ> =

∫φ^*QψdV = ∫(Qφ)^*ψdV = ∫Q^*φ^*ψdV

Покажем, что собственные функции эрмитовых операторов

взаимно ортогональны:

Q⁺ = Q

m|ψ_n> = <ψ_m|Qψ_n>

Qψ_m = q_mψ_m q_m^* = q_m

Qψ_n = q_nψ_n q_n^* = q_n

1) m|ψ_n> = q_m^*<ψ_m|ψ_n> = q_m<ψ_m|ψ_n>

2) <ψ_m|Qψ_n> = q_n<ψ_m|ψ_n>

q_m<ψ_m|ψ_n> = q_n<ψ_m|ψ_n>

(q_m − q_n)<ψ_m|ψ_n> = 0

<ψ_m|ψ_n> = δ_mn

Q⁺ = Q ⇔ <ψ_m|ψ_n> = δ_mn

1 = ∫φ^*φdV = ∫(Σc_mψ_m)^*(Σc_nψ_n)dV = (ΣΣc_m^*c_n)∫ψ_m^*ψ_n)dV =

= (ΣΣc_m^*c_n)δ_mn = Σc_m^*c_m = Σ|c_m|²

2.09.Представление операторов в матричной форме(35)

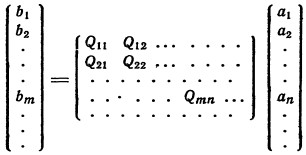
f = Qφ

φ = Σa_nψ_n

f = Σb_kψ_k

<ψ_m|ψ_n> = δ_mn

a_n = <ψ_n|φ>

b_k = <ψ_k|φ>

Σb_kψ_k = QΣa_nψ_n = Σa_nQψ_n

Σb_k <ψ_m|ψ_k> = Σa_n< ψ_m|Qψ_n>

Q_mn ≡ < ψ_m|Qψ_n> = ∫ψ_m^*Qψ_ndV

Σb_kδ_mk = Σa_nQ_mn

b_m = ΣQ_mna_n

полагаем суммирование по повторяющимся индексам !!!

(при этом упрощаются записи)

b_m = Q_mna_n

Qψ_n = q_nψ_n <ψ_m|ψ_n> = δ_mn

Q_mn = <ψ_m|Qψ_n> = q_n<ψ_m|ψ_n> = q_nδ_mn

(Q^*)_mn = (Q_mn)^*

(Q̃)_mn = Q_nm

(Q⁺)_mn = (Q̃^*)_mn = (Q_nm)^*

ψ = Σc_nψ_n

= <ψ|Qψ> = <Σc_mψ_m|QΣc_nψ_n> = c_m^*c_nΣΣ<ψ_m|Qψ_n> = ΣΣc_m^*Q_mnc_n

= c_m^*Q_mnc_n

можно рассматривать как произведение матрицы строки на матрицу и на матрицу столбец

Qψ = qψ

QΣc_nψ_n = qΣc_nψ_n

< ψ_m|QΣc_nψ_n> = <ψ_m|qΣc_nψ_n>

Σc_n< ψ_m|Qψ_n> = qΣc_n<ψ_m|ψ_n>

Σc_nQ_mn = qΣc_nδ_mn

Σ(Q_mn − qδ_mn)c_n = 0

(Q_mn − qδ_mn)c_n = 0

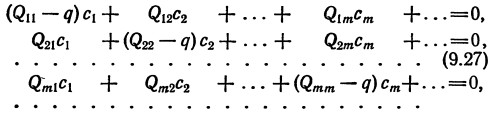
уравнение для собственных значений:

| Q_mn − qδ_mn| = 0

2.10.Алгебра операторов(44)

C = A + B

Cφ = (A + B)φ = Aφ + Bφ

C_mn = A_mn + B_mn

C = AB

Cφ = (AB)φ = A(Bφ)

C_mn = A_mkB_kn

C = (AB)^* = A^*B^*

C_mn = A^*_mkB^*_kn

C = (AB)^T = B^TA^T

C_mn = B^T_mkA^T_kn = B_kmA_nk = A_nkB_km = (AB)_nm

C = (AB)⁺ = B⁺A⁺

C_mn = (B⁺A⁺)_mn = B⁺_mkA⁺_kn = B^*_kmA^*_nk = A^*_nkB^*_km = (A^*B^*)_nm

A⁺ = A & B⁺ = B => (AB)⁺ = B⁺A⁺ = BA

A⁺ = A & B⁺ = B & AB = BA => (AB)⁺ = BA = AB

(iA)^* = −iA^*

(iA)⁺ = −iA⁺

b_m = Q_mna_n

b^*_m = Q^*_mna^*_n = Q̃^*_nma^*_n = a^*_nQ̃^*_nm = a^*_nQ⁺_nm

AB ≠ BA (не коммутирующие)

∎ A = ∂/∂x & B = x

ABφ = (∂/∂x)xφ = φ + x∂φ/∂x

BAφ = x(∂/∂x)φ ∎

AB = BA (коммутирующие)

AB = −BA (антикоммутирующие)

коммутатор:

[A, B] ≡ AB − BA

∎ [(∂/∂x), x] = (∂/∂x)x − x(∂/∂x) = 1 ∎

Qψ_n = q_nψ_n

Rψ_n = r_nψ_n

(Q + R)ψ_n = (q_n + r_n)ψ_n

(QR)ψ_n = Q(Rψ_n) = Q(r_nψ_n) = r_nQψ_n = r_nq_nψ_n

(RQ)ψ_n = R(Qψ_n) = R(q_nψ_n) = q_nQψ_n = q_nr_nψ_n

[QR] = QR – RQ = 0

AB = BA

Aψ^(a)_n = a_nψ^(a)_n

Bψ^(b)_n = b_nψ^(b)_n

ABψ^(a)_n = BAψ^(a)_n = Ba_nψ^(a)_n = a_nBψ^(a)_n

A(Bψ^(a)_n) = a_n(Bψ^(a)_n)

Bψ^(a)_n –собственный вектор A

BAψ^(b)_n = ABψ^(b)_n = Ab_nψ^(b)_n = b_nAψ^(b)_n

B(Aψ^(b)_n) = b_n( Aψ^(b)_n)

Aψ^(b)_n –собственный вектор B

2.11.Соотношение неопределенности(51) -можно пока пропустить !!!

∎

∆A = A − ∆B = B −