СТАТИСТИЧЕСКИЕ МОДЕЛИ (ЭКОНОМОМЕТРИЧЕСКИЕ)
Массивы данных, полученные в результате практических исследований после математической обработки, дают возможность вывести числовые значения коэффициентов корреляционной зависимости вида: Yi = a1X1,i+a2X2,i …+…ajXj,i , которое называется уравнение регрессии.
Где Х это имеющиеся показатели процесса, которые влияют на определяемый показатель Y. Далее, подставляя желаемые числовые значения коэффициентов показателей X, получаем предсказание следующих значений Y.
Пример постановки задачи
Выпускаемое четырнадцатью предприятиями изделие (или продукция, выпускаемая в четырнадцать временных периодов) имеет шесть параметров (например, рабочая частота изделия, энергопотребление, вес…). Основной показатель S (например, производительность изделия) зависит от этих параметров. Необходимо определить корреляционную зависимость, позволяющую предсказывать величину показателя S от всех шести параметров.

Практическое задание 1
Имеются исходные данные, которые были получены в результате ряда опытов или из сравнения подобных объектов. Количество опытов при этом должно быть, как минимум на один больше количества параметров объекта или процесса.

1.Занести данные на лист Excel и найти среднее значение всех факторов, позволяющее в дальнейшем использовать исследование безразмерных данных в соответствии с понятием коэффициент эластичности, позволяющего установить степень доверия к полученным результатам. Коэффициенты эластичности определяют и оценивают процентное изменение результата с увеличением или уменьшением каждого отдельного показателя на 1% при фиксированном значении остальных показателей и вычисляется как отношение среднего значения показателя к среднему значению результата.

2.Для вывода уравнения регрессии открыть и подключить (Файл, Параметры, Надстройки, Управление, перейти) надстройку Excel – пакет анализа.

3.Через меню Excel (Данные, Анализ данных) выполнить расчет и вывести итоги.



Получено достаточно высокое значение коэффициента корреляции 0,99, говорящее о том, что представленные данные хорошо описывают исследуемый процесс.
4.Вывести уравнение регрессии Y = A0 + A1 X1 + A2 X2 + …
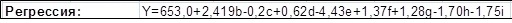
Коэффициент уравнения А0 находится в ячейке В36, значение его 653.0, далее коэффициент А1 в ячейке В37 со значением 2.419 и так далее;
5. Проверить полученное уравнение регрессии для каждого из ряда данных. В ячейке I1, строим формулу, получаем значение параметра Y для первого опыта.
=$B$36+$B$37*A1+$B$38*B1+$B$39*C1+$B$40*D1+$B$41*E1+$B$42*F1+$B$43*G1+$B$44*H1
Не забываем фиксировать адреса ячеек коэффициентов клавишей F4 клавиатуры. Копируем результат ячейки первой строки исходной таблицы на все строки.
6.Выявить параметры, имеющие низкую значимость, используем для этого показатель t- статистика и исключаем из таблицы данных параметры, имеющие низкое < │2 │ значение показателя, это переменные 1 и 5, соответствующие коэффициентам ячеек В37 и В41.

Уравнение при этом принимает вид:
=$B$36+$B$38*B1+$B$39*C1+$B$40*D1+$B$42*F1+$B$43*G1+$B$44*H1
Повторяем расчеты для обновленных данных, строим уравнение регрессии и выводим данные по каждому опыту в дополнительный столбец.
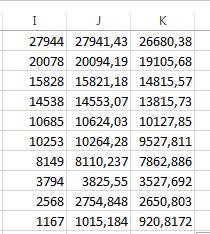
7. График зависимости показателя Y для опытов и на этом же графике интерполяционные зависимости, полученные из уравнений регрессии, если его построить, показывает совпадение расчётных данных с экспериментальными, следовательно, уравнением регрессии можно пользоваться для дальнейшего предсказания результатов.
Практическое задание 2
1.Заполнить ячейки EXCEL исходными данными.

2.Найти среднее значение всех факторов Х, позволяющее в дальнейшем использовать исследование в соответствии с понятием коэффициент эластичности (меню ГЛАВНАЯ, Редактирование, Другие функции, найти =СРЗНАЧ() и указать аргументом диапазон колонки чисел, затем скопировать функцию на все колонки):

3.Загрузить надстройку анализ данных (меню Данные, анализ данных, выбрать регрессия).
4.Настроить параметры в окне регрессии: входной интервал Y – указать выделением мышью диапазон Y, входной интервал Х указать выделением мышью все числовые значения Х, Параметры вывода можно оставить Новый рабочий лист или щелкнуть на свободное место текущего листа.

5.Получить коэффициенты уравнения регрессии и коэффициент корреляции.

Уравнение регрессии при этом выглядит следующим образом:
Y1=34,2199 -0,0603x1-1,77084x2-0,00143x3+1,089928x4-0,00035x5+0,01854x6
Подставляя в полученное уравнение числовые значения факторов можно предсказать дальнейшее изменение определяемого параметра Y.
6.Используя уравнение регрессии, получить значения выходного параметра для всех опытов: выбрать ячейку К2 занести формулу затем скопировать формулу на все опыты по столбцу.
=34,22-0,06*C2-1,77*D2-0,00143*E2+1,09*F2-0,00035*G2+0,01854*H2
7.Выделить диапазон J2:K15 и построить график.

Некоторые факторы демонстрируют плохую корреляцию с определяемым параметром, поэтому по таблице Стьюдента с вычисленным уровнем значимости и известным количеством опытов можно найти критическое значение параметра t-статистика и исключить некоторые из факторов. Проверка значимости модели регрессии также может быть проведена с использованием F-критерия Фишера. Значимость факторов может также продемонстрировать коэффициент эластичности.
8.Вычислить коэффициенты эластичности каждого из факторов. Коэффициент эластичности показывает, на сколько процентов в среднем изменяется результативный признак У, при изменении факторного признака Х на 1%. Коэффициент эластичности находится по формуле:
Е = Кх* Хср/Yср
где Кх – коэффициент уравнения регрессии при факторе, Хср и Yср средние значения фактора и параметра. В результате получены коэффициенты:
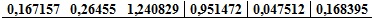
Оказалось, что лишь изменение факторов Х3 и Х4 может существенно влиять на результирующий показатель.
9.Исключить из ряда факторов те, у которых малая по абсолютному значения величина параметра t-статистика, это переменные Х1, Х2, Х5, Х6, и, снова получить коэффициенты уравнения регрессии и коэффициент корреляции;

Коэффициент корреляции при этом уменьшился, но все факторы имеют высокий уровень значимости и их достаточно для описания процесса. Уравнение регрессии при этом выглядит следующим образом:
Y2=28,89433-0,00124x3+0,83244x4
