Компьютерное моделирование химических взаимодействий - читать онлайн

Движущая сила химических процессов, протекающих в системах, – уменьшение свободной энергии этих систем. Например, для наиболее распространенных изобарно-изотермических условий эту роль играет энергия Гиббса.

В системе, находящейся первоначально в неравновесном состоянии, могут протекать различные химические реакции, в результате которых будут образовываться различные химические вещества.

Общая энергия Гиббса системы складывается из энергий Гиббса всех веществ, которые в нее входят. Другими словами, она является функцией числа молей входящих в нее веществ, а также давления и температуры.

В итоге, при заданных параметрах состояния в системе образуются такие вещества и в таких количествах, при которых энергия системы становится минимальной. Наша задача заключается в том, чтобы определить, что это за вещества и каковы их количества. Для этого нам нужно найти минимум функции, выражающей энергию Гиббса системы.

Поскольку в точке минимума функции многих переменных частные производные по всем переменным обращаются в ноль, то составим систему уравнений:

Так как G(n₁, … , n_N) – экстенсивная функция, т. е. является однородной первого порядка, то по теореме Эйлера имеем:

С другой стороны, из определения химического потенциала:

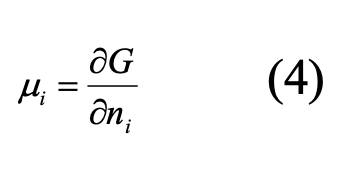
В нашем случае на решение данной системы накладываются условия материального баланса: количество вещества в системе должно оставаться постоянным. Это значит, что искать минимум функции надо не во всей области существования, а в той области, которая задается ограничениями. Функция в этом случае достигает минимума в точке экстремума (если он лежит в этой области), либо на границе области.

Поясним на примере. Рассмотрим систему, образованную из двух химических веществ: SO₂ и N₂.

Эта система состоит из трех химических элементов: S, O и N. В результате взаимодействия из этих веществ могут образоваться любые вещества, состоящие из этих трех элементов: оксиды серы и азота, соединения серы и азота и, наконец, соединения серы, азота и кислорода. Составим матрицу {a_i,_j}_MxN материального баланса для этих веществ:

Запишем материальный баланс системы в следующем виде:

Где n_j⁰ – количество молей элемента j, которое определяется количеством веществ, из которых первоначально состояла система; M – количество химических элементов в системе.

Кроме того, на решение нашей задачи накладывается еще одно условие: равновесные количества веществ не должны быть отрицательными. Наша система уравнений и неравенств примет следующий вид:

Таким образом, решив данную систему, мы определим количества веществ, образующихся в системе, когда она приходит в состояние равновесия.

В общем случае химический потенциал складывается из:

Рассмотрим случай, когда вещества в системе существуют в индивидуальном состоянии, то есть не растворяются друг в друге. В этом случае в уравнении (7) второй член станет равным нулю, и химический потенциал любого вещества в системе будет равен его энергии Гиббса. Назовем расчет равновесного состава системы, состоящей из индивидуальных веществ (фаз), фазовым расчетом.

Сущность решения заключается в определении коэффициентов функции в области, определяемой набором равенств и неравенств таким образом, чтобы значение функции было минимальным. В результате этого расчета мы будем иметь набор n_i, то есть равновесные количества веществ в системе.

В случае, когда вещества в системе образуют растворы, необходимо учитывать их активности при расчете химического потенциала.

В результате решения этой задачи мы также получим набор n_i (i=1…N) – количество каждого вещества, образующегося в системе, когда она приходит в состояние равновесия [1].

Описанный подход можно назвать термодинамическим моделированием равновесного состава. Он является той самой базой, на которой строятся расчеты фазово-химических взаимодействий.

Второй неотъемлемой частью является набор термодинамических характеристик веществ, как изначально входящих в исследуемую систему, так и способных образовываться в систему в результате их взаимодействия и изменения параметров состояния системы.

Существует два фактора, влияющих на соответствие расчетных данных реальному составу равновесной системы. Один из них (метод расчета) мы уже рассмотрели. Другим являются исходные данные, участвующие в расчете – их полнота и точность [2, 3].

Каким бы точным ни был метод расчета – его результаты будут ошибочными, если ошибочны исходные данные, закладываемые в него.

В нашем случае исходными данными являются термодинамические характеристики всех возможных химических веществ, способных образоваться в системе, а именно:

• термодинамические константы стандартного состояния: ∆^fH, ∆^fG, S (любые две из них достаточны);

• термические константы фазовых переходов (при наличии переходов): T_tr, ∆H (или ∆S, т.к. ∆H = T_tr ∆S_tr);

• температурно-зависимые функции G(T) (при фиксированном, стандартном значении P = P₀ = 1 бар).

Несмотря на кажущееся обилие представленной информации, данные нередко противоречивы, не согласованы, неполны или вовсе отсутствуют.

Выявление этих ошибок в данных и их устранение представляет собой самостоятельную многослойную и сложную проблему. Давайте сформулируем основные требования, которым должны удовлетворять соответствующие базы термодинамических данных.

Исходное требование – достаточная полнота базы по спектру содержащихся в ней веществ. При моделировании поведения системы (как и в случае применения экспериментальных методов исследования) неучет отдельных веществ, способных в ней образовываться, может приводить не только к неполному, но и к искаженному представлению о свойствах всей системы в целом. В то же время ошибочный учет соединений, которые при рассматриваемых условиях не могут образовываться в системе, не нарушает корректности модели.

Очевидно и другое условие полноты – по набору заданных термодинамических характеристик вещества базы, необходимых для корректного построения его термодинамического описания в рассматриваемом диапазоне значений параметров состояния.

Термодинамические характеристики веществ чаще всего определяют экспериментально по данным ряда сложных реакций. Это приводит к необходимости «внешнего» согласования данных всех веществ, входящих в базу данных.

Также согласованность должна быть и «внутренней» – энтальпии, энергии Гиббса и энтропии веществ всегда должны удовлетворять тождеству: ∆H = ∆G + T∆S для любой возможной реакции между ними.

И, наконец, еще одно ключевое требование – необходимая достоверность собственно термодинамических характеристик веществ базы. Она определяется качеством соответствующих составляющих – «индивидуальных» и «реакционных», характеризующих в совокупности корректность и точность термодинамического описания вещества.

Отметим, что рассмотренные требования, которым должна удовлетворять база данных, оказываются взаимосвязанными. Если, например, исходные данные противоречивы или недостаточно надежны, то достичь внутренней, и тем более их внешней согласованности, невозможно. Ежели требуемые термодинамические характеристики не определены или настолько не согласованы, что не могут быть включены в базу, то полноту и достоверность данных обеспечить не удается.

Ещё один из аспектов условия полноты термодинамических данных – относительно всего поля устойчивого существования соединения – особо актуален при исследовании неорганических систем в широком диапазоне давлений и, что наиболее существенно, температур. Вызвано это потребностями как чисто научного, так и технологического планов не только при "нормальных", близких к стандартным, условиях, но и, в первую очередь, в области высоких температур (порядка 1000°C и выше). В литературе редки, к сожалению, случаи полноты такой информации (точек и областей полиморфных и агрегатных переходов, их термодинамических характеристик, температурных зависимостей теплоемкости) и её согласованности.

На основании многолетней работы нами были собраны базы термодинамических данных, обладающие требованиями химической полноты, термодинамической полноты и объективной точности содержащейся в них информации.

Кроме того, ведется постоянная работа над базами данных, в результате чего происходит их пополнение и улучшение.

Методы расчета термодинамических характеристик

Случаются ситуации, когда в исследуемых системах образуются такие соединения, которые на сегодняшний день малоизучены. Их термодинамические характеристики неполны, а то и вовсе отсутствуют. В таких случаях возможно применение различных расчетных методик, что является отдельной непростой задачей.

С одной из таких системы мы столкнулись, когда начали изучать проблемы, возникающие в трубопроводах при добыче и транспортировке нефти.

Одной из трудностей в термодинамическом исследовании таких систем является образование в них газовых гидратов – соединений, которые нестабильны в обычных условиях, а потому их свойства мало изучены.

Вследствие проведенной работы [4] был осуществлен анализ существующих подходов к исследованию свойств газогидратов и получены их термодинамические характеристики, необходимые для дальнейших расчетов.

Изучение методов расчета не рассматривается в данном пособии, предлагаем заинтересованным читателям начать с [5].

В данном разделе мы введем терминологию, которой будем пользоваться в следующих частях книги для описания исследования реальных систем методом термодинамического моделирования. Кроме того, рассмотрим виды термодинамических расчетов и их области применения.

Фазовый расчет. Представьте такие условия, при которых вещества в системе могут химически реагировать между собой, но не могут образовывать растворов. На практике приближенные к этому условия могут быть реализованы в системе, состоящей из веществ, находящихся в твердом состоянии.

Термодинамическая модель такой системы предполагает, что все вещества существуют в системе только в индивидуальном состоянии, то есть их активности равны единице, не образуется ни твердых, ни жидких, ни газообразных растворов.

Фазовый расчет можно также разделить на два: без возможности образования газов и с возможностью образования газов.

Первый случай реализуется в условиях, когда в системе невозможно газообразование: толща материала, высокие давления и пр.

Второй случай, когда образование газов возможно, однако при этом газы не образуют растворов, а существуют в индивидуальном состоянии, является, по сути, упрощением реальных систем.

Фазовый расчет с газовой фазой позволяет определить наиболее устойчивые соединения, вносящие самый весомый вклад, определяющий движущую силу процесса.

Для быстрой оценки фазовых превращений в различных системах нами был разработан инструмент под названием «Фазовый калькулятор», о котором будет рассказано далее в книге.

Расчет растворов в конденсированных фазах. Следующим шагом в приближении идеальной системы к реальной будет учет возможности образования растворов в конденсированных фазах. Рассмотренный ранее фазовый расчет показывает, какой набор конденсированных фаз реализуется в системе при конкретных параметрах состояния (температуре и пр.). Часть этих фаз, либо все вместе, могут образовывать растворы.

Отсутствие общей теории растворов не дает возможность расчетным путем определить, какие из фаз будут образовывать растворы. Поэтому информация об этом должна быть заложена изучающим систему, исходя из опыта. К примеру, при синтезе неорганических стекол соединения образуют раствор. При синтезе керамики, цемента и пр. возможно лишь частичное образование растворов. А при синтезе огнеупорных композиций, восстановлении металлов из руд и пр. образование конденсированных растворов крайне маловероятно.

Учет возможности образования растворов сильно усложняет химизм процесса, поскольку в растворе возможно образование большого количества зависимых соединений (в отличие от количества индивидуальных фаз, не связанных правилом Гиббса).

Расчет газовых растворов. В условиях, когда химические взаимодействия происходят в газовой фазе, либо на границе конденсированных фаз с газовой, поведение системы также усложняется.

Во-первых, в таких условиях химическое взаимодействие конденсированных соединений возможно с образованием газообразных продуктов. Во-вторых, происходит частичное испарение конденсированных фаз. В-третьих, в самой газовой фазе возможно протекание химических взаимодействий с образованием новых соединений. И наконец, газообразные вещества образуют раствор, что также усложняет моделирование подобных систем.

Расчет водных систем. Особенность систем, в которых образуются водные растворы, заключается в том, что такие растворы содержат большое разнообразие ионных комплексов. Каждый такой комплекс имеет термодинамические характеристики и вносит свой вклад в общую энергию системы.

Учет всего разнообразия образующихся комплексов из исходных соединений позволяет с высокой точностью вычислять термодинамические свойства водной системы, а значит, и ее итоговый равновесный состав в заданных условиях.

Данный расчет позволяет моделировать процессы коррозии, процессы комплексообразования в сложных растворах, процессы извлечения полезных ископаемых (например, железо-марганцевых конкреций из морской воды), процессы охлаждения атомных электростанций (как процессы растворения, так и образования осаждений), исследования в глубинах океана (например, определение состава воды и дна Марианской впадины по составу на поверхности), ряд экологических задач, связанных с водой, химическую отмывку отложений и многое другое.

Структуру расчетов изобразим на следующей схеме:

Вид расчета или их сочетание позволяют выбирать уровень ограничений на физико-химическую систему: возможно ли в ней образование различных видов растворов или фаз.

Состав подключаемой в расчете базы данных определяет спектр возможных продуктов взаимодействия.

Сочетание вида (видов) расчета и базы (баз) данных позволяет учесть различные условия протекания физико-химических взаимодействий и максимально приблизить модель к реальности.

Более подробно о том, как это происходит, мы опишем далее на примерах расчета конкретных систем.

Описанный метод расчета химических равновесий имеет ряд особенностей, которые необходимо учитывать при его использовании.

Полнота составляющих систему соединений. Вычисляя состояние равновесия системы при заданных условиях, мы учитываем максимально возможное количество веществ, способных образоваться из начального состава системы. Другими словами, веществ из тех же химических элементов (что и первоначальные), существующих в природе. Для каждого такого вещества нам необходимо знать все его термодинамические характеристики в исследуемом температурном диапазоне.