Киты и люди - читать онлайн

В этом рассказе мы узнаем о многих интересных беседах Льюиса Доджсона с Долом и Зюлом; некоторые из них состоялись в присутствии Александра.

Как ты помнишь, капитан Александр согласился взять молодых великанов матросами на корабль «Быстрые паруса» при условии, что они будут продолжать учебу у Его Преподобия. Получат от него задания на время плавания, а потом – отчитаются об их исполнении.

Капитан строго следил за тем, чтобы в свободное от вахты время Дол и Зюл занимались по программам Его Преподобия. Много им помогал, подолгу объяснял непонятное, а в портах покупал необходимые научные книги и журналы.

Каждый раз, возвращаясь из похода, Дол и Зюл встречались с Л. Д. (так они называли Льюиса Доджсона). Их встречи проходили обычно в тёплой, непринуждённой обстановке. У Его Преподобия было приподнятое настроение, он был рад видеть молодых великанов, был весел и оживлён, подолгу расспрашивал своих любимцев о путешествиях, и те с удовольствием делились впечатлениями о морских странствиях, много шутили и смеялись. Но вот начинались занятия, Л. Д. становился строгим профессором, а Дол и Зюл – прилежными и старательными учениками.

Уроки эти, как правило, превращались в беседы, во время которых преподаватель задавал вопросы, заставляющие Дола и Зюла более глубоко понять обсуждаемые проблемы. Капитан Александр, который также иногда присутствовал на этих занятиях, внимательно слушал Его Преподобие и своих подопечных и, как правило, молчал. Но мы-то с тобой знаем, что Александр часто знал гораздо больше, чем говорил.

Сохранились записи капитана об уроках, на которых он присутствовал. Записи эти по форме напоминают диалоги знаменитых греческих философов Сократа и Платона. Капитан называл их «диалогами Доджсона». Занятия касались многих важных вопросов изучения окружающего нас мира. Я выбрал несколько таких бесед для моего рассказа. Конечно, чтобы познакомиться с диалогами Доджсона и хорошенько разобраться в них, тебе, мой друг, а также вам, мои юные читатели, придется изрядно попотеть и пошевелить мозгами. Если у вас, например, нет склонности к логике, математике, физике или биологии, – не стоит расстраиваться из-за этого. Одни любят «включить голову», другие живут больше сердцем. Имеют другие способности – к музыке, поэзии, танцам, к изучению языков. Есть и такие, кто любит что-то мастерить, делать своими руками. Или, например, поиграть в войнушку. Мы все разные, а были бы одинаковыми – жизнь стала бы совсем неинтересной и очень скучной. В общем, если тебе не хочется решать головоломные задачки, просто пропусти этот раздел, и ты ничего не потеряешь. Переходи к следующему рассказу, в котором ты сможешь познакомиться с новыми приключениями капитана Александра. А кто хочет последить за беседами молодых великанов со своим наставником – в добрый путь.

Беседа первая. Парадоксы

– Знаете ли вы, молодые люди, что такое парадокс? – спросил Л. Д. своих учеников.

– Парадокс – это положение, резко расходящееся с общепринятыми, устоявшимися нормами и мнениями, – ответил Дол.

– Парадокс – оригинальное, неожиданное высказывание, противоречащее самому себе, здравому смыслу или кажущееся нелогичным, – добавил Зюл.

– Проверим, насколько хорошо вы это понимаете, – сказал Л. Д. суровым голосом. Если бы кто-то наблюдал эту беседу со стороны, то сумел бы заметить лукавый прищур глаз Л. Д., спрятанных за профессорскими круглыми очками на носу.

Л. Д. Рассмотрим парадокс брадобрея.

– Кто такой этот брадобрей?

– В далёкие времена, когда не было электробритв и безопасных лезвий, бриться самому было очень сложно, и мужчины ходили к брадобрею – тому, кто брил бороды.

Л. Д. изложил классический парадокс брадобрея:

– Одному деревенскому брадобрею приказали брить всякого, кто сам не бреется, и не брить тех, кто сам бреется. Кто бреет брадобрея? Если брадобрей не бреется сам, то он должен себя побрить, а если он бреется сам, то согласно второй части приказа, он не должен себя брить. Возникает логическое противоречие. Как поступить брадобрею с самим собой? Можно ли ответить на этот вопрос?

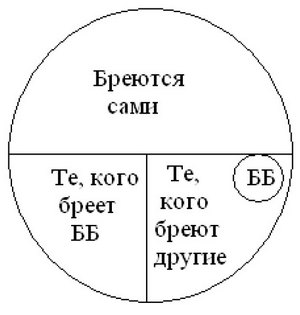
Вот что ответили ему Дол и Зюл после довольно долгих размышлений.

Дол. Нарисуем круг, внутри которого располагаются все жители деревни, которые бреются. А вокруг расположим других жителей деревни, которые не бреются (монахи, женщины, дети). Разделим круг на две части: вверху расположим тех, кто бреется сам, внизу – тех, которых бреют. Первая часть приказа – «брить всякого, кто сам не бреется», разрешает ему брить и того, кто сам бреется, то есть самого себя. Поэтому брадобрея (ББ) можно поместить в верхней части круга.

Зюл. Теперь нарисуем тот же круг, в котором нижняя часть разбита на две части. Слева распложены те, которых бреет ББ, а справа – те, которых бреют другие. Вторая часть приказа – «не брить, тех, кто сам бреется», разрешает ему брить тех, кто слева в нижней части круга. Сам он может быть побрит приятелем и располагается справа внизу. Если одновременно действуют оба поручения, то ББ нет места в круге.

Дол. И он может быть только за пределами круга. Значит, он не бреется вообще: он – или монах, или подросток, или женщина.

Л. Д. А если в деревне одни только бреющиеся мужчины?

Дол и Зюл. Тогда таких брадобреев нет. Вопрос некорректный! – сказали вместе Дол и Зюл.

Казалось, Л. Д. был удовлетворён ответами учеников, но глаза за стёклами его очков опять лукаво заблестели.

Л. Д. Неплохо, неплохо! Посмотрим теперь, как вы справитесь с парадоксом «Крокодил и Женщина».

На берегу стояла египтянка с ребёнком. Неожиданно Крокодил выпрыгнул из воды и выхватил ребенка.

Женщина плакала, умоляла Крокодила вернуть ребёнка. Крокодил был растроган и тоже плакал (крокодильими слезами, конечно).

– Я дам тебе шанс получить ребёнка, – сказал он. – Угадай, отдам я тебе его или нет. Ответишь правильно – верну ребёнка, неправильно – не верну!

Женщина подумала и ответила:

– Ты не отдашь мне ребёнка!

Что ответил Крокодил?

Дол. Крокодил ответил:

– Ты сказала либо правду, либо неправду. Если то, что я не отдам ребёнка, – правда, я не отдам его, так как иначе сказанное не будет правдой. Если сказанное – неправда, значит, ты не угадала, и я не отдам ребёнка по уговору.

Парадокс, к сожалению, печально разрешён.

Л. Д. Не совсем так. У матери могут быть другие рассуждения – попробуй ты, Зюл.

Зюл. Женщина убеждена в противоположном:

– Если я сказала правду, ты отдашь мне ребёнка по уговору. Если же я не угадала, что ты не отдашь ребёнка, то ты должен его отдать, иначе сказанное мною не будет неправдой.

Парадокс разрешён в пользу матери.

Л. Д. Что же должен сделать Крокодил?

Дол, Зюл. Обещание внутренне противоречиво, поэтому оно невыполнимо в силу законов логики.

Л. Д. А если бы женщина ответила – ты отдашь мне ребёнка?

Дол, Зюл. Тогда бы не было парадокса!

Л. Д. А ну-ка расскажите, ребята, какие ещё парадоксы вы знаете?

Дол, Зюл. По вашему заданию, учитель, мы познакомились с очень многими логическими и физическими парадоксами: парадокс кучи, парадокс Ахиллеса и Черепахи, парадокс рюмки водки, парадокс всемогущего существа, парадокс лысого[5].

Мы выяснили, что существуют неразрешимые парадоксы и противоречия, но есть и такие, которые легко разрешаются в реальной жизни.

Л. Д. Какой парадокс вам нравится больше всего?

Зюл. Парадокс слуги. «Прикажите слуге не слушаться Вас». Не слушаясь вас, он ослушается приказа, так как он исполняет его, не слушаясь вас.

Дол. Мне нравится парадоксальное высказывание Бернарда[6]: «Не поступай с другим так, как хочешь, чтобы он поступил с тобой, у вас могут быть разные вкусы».

А у вас есть любимый парадокс, учитель?

«Ахиллес никогда не догонит черепаху»

Л. Д. Король неразрешимых парадоксов – высказывание Евбулита из древней Греции: «Я лгу», – торжественно сказал Л. Д., гордо подняв голову. – Если высказывание ложно, то говорящий сказал правду, и значит, сказанное им не является ложью. Если же высказывание не является ложным, а говорящий утверждает, что оно ложно, то это его высказывание ложно. Оказывается, таким образом, что, если говорящий лжёт, он говорит правду, и наоборот.

– Ты сказал, вернее – Дол с Зюлом сказали, что бывают разрешимые парадоксы.

– Бывают ли такие высказывания, которые кажутся парадоксальными, но которые можно объяснить? Помнишь, в одном из рассказов мы говорили, что капитан Александр вышел из «неизвестного известного порта»? Определения «известный» и «неизвестный» противоречат друг другу, но оба относятся к одному конкретному порту. Так «известным» был этот порт или «неизвестным»? Порт был известным в том смысле, что о нём многие слышали, но сейчас никто уже не может вспомнить, из какого порта в тот раз вышел на своем корабле капитан Александр. И в этом смысле – порт неизвестен. Как видишь, после соответствующего объяснения, определения приобретают разный смысл, перестают противоречить друг другу и поэтому могут совмещаться.

Таким же образом можно было бы разрешить парадокс брадобрея. Сформулируем его так: «Брадобрею приказали брить всякого, кто сам не бреется, и не брить тех, кто сам бреется у себя дома и в любом другом помещении, но не в брадобрейной». Брадобрей сможет сам побриться у себя в брадобрейной.

– А можно сказать так – «известный неизвестный порт»?

– Возьмем порт Лисс или порт Зурбаган. Оба порта стали известны из книг Александра Грина, русского писателя, которого ты, конечно, знаешь, а до того – и Лисс, и Зурбаган были никому не известны.

– Я тоже могу придумать парадоксы: «маленький большой великан», «строгий нестрогий капитан Александр», «вкусная невкусная каша»…

– Это, конечно, очень похоже на парадоксы. Но скорее это «оксюмороны» (оксюморон – умная или остроумная глупость). Слово, конечно, довольно заковыристое, но тебе неплохо было бы запомнить его, если мы обсуждаем парадоксальные изречения. Оксюморон – это сочетание слов противоположного значения (сочетание несочетаемого), способ разрешения неразрешимых ситуаций. Вот тебе примеры оксюморонов: «известный неизвестный и неизвестный известный порты», о которых мы говорили, «обыкновенное чудо», «праведная ложь», «конец вечности», «назад в будущее», «вверх по лестнице, идущей вниз».

– «Красивая некрасивая девочка»…

– Кого ты имеешь в виду?

– А помнишь, ты читал мне стихи о некрасивой девочке?[7] О том, какая она живая и весёлая. И как она всем понравилась.

– Это девочка из стихотворения Заболоцкого «Некрасивая девочка». Молодчина, хорошо!

– Ещё – «правдивый взгляд лжеца».

– Это не оксюморон, это парадокс. Объясни, в чем парадокс.

– Ты говорил, что глаза лжеца всегда его выдают. И говорят правду о том, что он лжёт [8].

– Прекрасно. Здорово придумано. «Глаза лжеца говорят правду: «Я – лжец»». Это очень похоже на парадокс Евбулита из Милета, о котором говорил Его Преподобие с молодыми великанами Долом и Зюлом.

Но давай продолжим, потому что наши герои как раз сейчас обсуждают другие, тоже очень интересные вопросы.

Беседа вторая. Арифметика

Л. Д. С логикой у вас всё в порядке, дорогие друзья. Посмотрим, как вы справитесь с арифметикой. Вспомним считалочку Алисы[9]: четырежды пять – двенадцать, четырежды шесть – тринадцать и т. д. Эта считалочка даёт Алисе «таблицу умножения» до двадцати. Расскажите, как устроена эта парадоксальная считалочка и продолжите её от двадцати и далее. Вам нужно сделать то, с чем Алиса не справилась.

Дол. Давай, Зюл. Твоя очередь.

Зюл. Детям нужно максимально упростить таблицу умножения. Чтобы было проще запоминать. Для этого её нужно немного изменить, сохранив принципы считалочки Алисы. Вот эта таблица умножения: четырежды пять – пятнадцать,

четырежды шесть – шестнадцать,

четырежды семь – семнадцать.

Пропустим несколько строчек. Далее будет:

четырежды десять – сто десять,

четырежды одиннадцать – сто одиннадцать.

Далее:

четырежды двадцать – сто двадцать,

четырежды двадцать один – сто двадцать один.

Кроме того, надо расширить первую, самую простую считалочку, покажу это на примере умножения на три:

трижды пять – пятнадцать,

трижды шесть – шестнадцать и т. д.

Л. Д: Забавная таблица умножения. И ты утверждаешь, что эта смешная считалочка имеет какой-то смысл?

Зюл. Конечно, о, мой высокочтимый учитель!

Далее Зюл рассказал, как устроена эта таблица умножения[10].

Если ты любишь математику, тебе будет интересно познакомиться с этой парадоксальной арифметикой и попытаться понять, как она устроена.

Л. Д. Молодец, Зюл. Ты сумел правильно разобраться в считалочке Алисы. И даже дополнить её. Как видите, ребята, даже в такой простой дисциплине, как арифметика, которую изучают дети младших классов, мы с вами можем найти очень много интересного и даже неожиданного.

Зюл. Да нет же, учитель. Считалочка Алисы – вовсе не арифметика. В ней нет никакого смысла. И доказательство моё ровно ничего не доказывает. Это просто игра ума, шутка.

Л. Д. Не скромничай, Зюл. В твоем доказательстве нет логических противоречий. Это арифметический парадокс. После того как доказана истинность шуточной считалочки, она становится полноправной таблицей умножения. Хотя кажется полной ерундой. Друзья мои, мы с вами занимаемся не парадоксами, а Парадоксизмом – современным движением, основанном на использовании парадоксов в науке и творчестве. Одним из его положений является: «Нет бессмысленных высказываний. Любое бессмысленное высказывание имеет смысл». Например: «Человек создан для счастья, как пингвин для полета». Ну чего вы хохочете? И наоборот – «Любое осмысленное высказывание не имеет смысла», например: «Любить любовь любовью люби». Сами разберётесь, что означает и то, и другое. Наш лозунг: «Всё возможно, невозможное – тоже». Мы переводим невозможное в возможное, преобразуем ненормальное в нормальное, объясняем необъясняемое. Когда-нибудь немного позже мы поговорим о том, как важно стремиться к невозможному. А пока я попробую повеселить вас примерами забавных парадоксизмов:

Так неожиданным возвращением к парадоксам и ко всеобщему удовольствию закончилась эта довольная сложная беседа об арифметике.

Беседа третья. Сила тяжести

Л. Д. Сменим тему, мои юные ученики, и поговорим об основах физики. Вижу, вы – не против. Я давал вам задание ответить на вопрос: может ли человек добраться до центра Земли? Ведь сила притяжения по мере приближения к центру нашей планеты должна возрастать и человек может быть раздавлен силой тяжести. Кто ответит? Может быть ты, Зюл, будущий физик и математик?

Зюл. Ответ на этот вопрос дал нам великий Галилео[12], о мой учитель. А найти его в книгах помог нам капитан Александр. Когда тело падает через тоннель к центру Земли, его скорость возрастает, а сила притяжения уменьшается. Тело долетит до центра Земли за 36 минут (если, конечно, в тоннеле нет воздуха). Будет ли человек падать, как Алиса в кроличью нору, или тихонечко спускаться, вес его будет уменьшаться, пока в центре Земли он не станет равным нулю. Так что это путешествие, если оно, конечно, возможно, будет для человека совершенно безопасным. При дальнейшем падении скорость тела будет уменьшаться, а сила притяжения возрастать. Пока оно не долетит до поверхности земли, но уже с другой стороны. Всего на этот полёт будет потрачено 72 минуты.

Дол. Изучая вопрос о падении в тоннель к центру Земли, мы узнали об интересном предположении астронома Фламмариона, которое также помог нам найти капитан Александр. Если просверлить в земле совершенно прямой тоннель из Санкт-Петербурга в Сантьяго, например (как на рисунке), и пустить по этому тоннелю поезд, предварительно выкачав воздух, то поезд будет сам под действием силы тяжести разгоняться, достигнув в середине тоннеля необыкновенной скорости. Потом он начнет тормозиться и остановится как раз в Сантьяго, потратив на этот путь 72 минуты без использования паровоза. Ровно столько, сколько потребуется падающему телу для полёта через центр земли. Невероятно, но факт.