Физика информации
Имеются различные понятия определения информации. Есть философские понятия информации, определение информации в широком смысле как понимают люди, в узком научном смысле какой ему придал Шеннон и другие подходы.
ГОСТ Р 50922—96 определяет информацию как сведения о лицах, предметах, фактах, событиях, явлениях и процессах независимо от формы их представления
Рассмотрим физическую модель информации. Введем понятие информация – физическое поле.
Физическим полем называется область пространства, где проявляют себя физические, достоверно зарегистрированные и точно измеренные силы. В рамках современной физики известны и изучены четыре вида материальных полей: гравитационное, электромагнитное – магнитное и/или электрическое, поля сильных взаимодействий – ядерное, слабых взаимодействий (Рис.1).
Имеются силовые поля в веществе и в средах, которые проявляются только при наличии материальной среды. К таким полям относятся: акустические, вибрационные, гидроакустические поля и др. Эти поля отсутствуют, если будет отсутствовать среда. Они характеризуются давлением, скоростью, ускорением и другими характеристиками.
Рассмотрим ряд элементарных примеров для понятия «информация – это поле».
Человек видит окружающий мир это отражение от объектов в видимом спектре электромагнитного поля. Восприятие или создание звука это акустическое поле. Электрический ток – движение заряженных частиц под действием электрического или электромагнитного поля. Передача и прием сообщений по каналам связи обеспечивается в различных частотных диапазонах электромагнитного поля.
Образец вооружения и военной техники. Пока он закрыт полностью – нет информации. Движение, работа, функционирование узлов, агрегатов все это создает физические поля, значит, есть информация.
Перемещение материальных частиц и тел, их информационное взаимодействие происходит в поле тяготении, в гравитационном поле.
Процессы в микромире происходят в полях сильных и слабых взаимодействий. Ряд примеров легко продолжить, но на каком конкретном случае мы бы ни остановились, принципы и идеи определяющие, раскрывающие физические процессы создания информации и ее отображения, везде оказываются одинаковыми – это физическое поле. Следовательно, физическое поле как и информация, существует независимо от того воспринимается или регистрируется кем то или чем то.
Физическое поле это особый вид материи. Материя – объективная реальность, данная нам в ощущениях. Считается, что материя существует либо в виде вещества, либо в виде поля.
Основное отличие поля от тел или частиц заключается в том, что оно локализовано в пространстве. Для описания состояния частицы требуется задать ограниченное число параметров равное числу степеней свободы. (Для материальной точки это радиус-вектор r, задаваемый тремя проекциями на оси координат).
Чтобы знать параметры поля в любой точке пространства нужно задать закон, по которому меняется поле в пространстве и начальные параметры. Поле проявляется в силовом воздействии на тела или частицы (действует сила F). Одной из важных количественных характеристик поля, является напряженность. Напряженность поля определяется как отношение силы, действующей на тело, к величине той количественной характеристики, которая участвует в создании поля и определяется полем, поэтому напряженность называют силовой характеристикой поля. Существенно, что напряженность поля является векторной величиной, так же как и сила, через которую она определяется. Таким образом, поле задано, если в каждой точке пространства известна его напряженность.
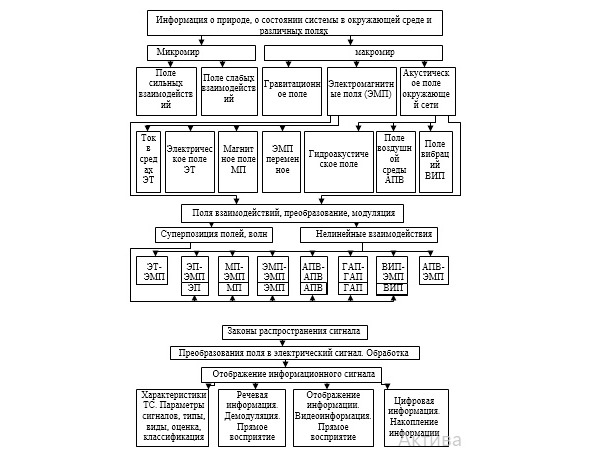
Рис.1 – Структура физических полей, информация, направление защиты.
Создание, формирование поля, его распространение, регистрация, прием, измерение характеристик поля и преобразованного поля в электрический сигнал для отображения информации – этот физическая суть создании и получение информации.
Если использовать конструктивный подход к понятию информации и рассматривать понятие «информация» как объект защиты, то этот объект будет описываться меньшим числом факторов, свойств, признаков.
Поэтому целесообразно информацию представить в виде многообразия физических полей, которые отражают среду переноса проявления источников информации, но не сущность информации.
Физические поля (информация) формируются, создаются природой, техническими системами, средствами (ТС), биологическими объектами.
Технические средства имеют так называемые техногенные физические поля. Эти поля несут данные, сведения, как о самом техническом средстве, так и о содержание сведений, которые циркулирует в техническом средстве (например, речевое сообщение в средствах связи, сведения в видеосистемах, в ЭВМ и др.)
Информация – это не только физическое поле определенного вида, но это и так называемые поля взаимодействия электромагнитных полей, поля взаимодействия электромагнитных и акустических полей. При этом наблюдается два вида взаимодействий суперпозиция полей, волн и нелинейные взаимодействия (Рис.1).
Принцип суперпозиции. В общем случае, принцип суперпозиции – это допущение, согласно которому результирующий эффект сложного процесса воздействия эквивалентен сумме эффектов от каждого воздействия в отдельности. Разумеется, это определение предполагает, что эффекты не влияют друг на друга.
Сформулированный принцип справедлив, если система описывается линейными уравнениями. Слабое гравитационное поле с хорошей точностью подчиняется принципу суперпозиции. Для ряда случая электромагнитных полей принцип суперпозиции применим к системе, описываемой нелинейными уравнениями, т.е. меняющейся под действием внешних эффектов, принцип суперпозиции неприменим. Примером нарушения принципа суперпозиции может служить магнитное поле в ферромагнетике. Другой пример – свет (сильное световое поле) в среде. Такое поле может генерировать в среде за счет нелинейного взаимодействия с ней свет на длине волны в два, три или более раз меньшей.
Сильное гравитационное поле не подчиняется принципу суперпозиции, поскольку оно описывается нелинейными уравнениями Эйнштейна. Разделы физики, которые изучают явления, в которых нарушается принцип суперпозиции, обычно называют нелинейными. Например, нелинейная оптика.
В математической модели будут рассмотрены слабые гравитационные, электромагнитные, акустические поля, к которым принцип суперпозиции применим. В дальнейшем рассмотрим суперпозицию, и взаимодействия таких полей: электромагнитного поля (ЭМП), электрического поля (ЭП), магнитного поля (МП), гидроакустического поля (ГАП), акустического поля (АПВ), вибрационного поля (ВП). Примером такого взаимодействия может являться любое излучение акустическое или электромагнитное, в реальных условиях распространения при отражениях.
Нелинейные взаимодействия
Рассмотрим, приведем ряд примеров описание преобразований составляющих ЭМП с ЭМП при наличии нелинейных элементов или структур. Кроме того, будем рассматривать взаимодействие акустического и вибрационного полей с электромагнитным полем на нелинейных элементах и нелинейных средах. Обратимся к рисунку 1.
ЭТ-ЭМП. Классическим примером такого взаимодействия является модуляция электрическим током излучения переменного электромагнитного поля. Это передающие средства связи, телекоммуникаций, радиолокации, телевидения и т. д.
ЭП-ЭМП, МП-ЭМП, Составляющая ЭМП – электрическое поле (ЭП) и магнитное поле (МП) воздействует на радиотехнические цепи радиопередающих устройств, где путем наводки или воздействия на нелинейные элементы транспонируются в другой частотный диапазон. Кроме того, наводятся на линии связи, электропитания и коммуникаций.
ЭМП-ЭМП. Наиболее объемное взаимодействие полей на нелинейных структурах. Охватывает широкий частотный диапазон электромагнитных волн. Воздействие на электрические цепи аналогично ЭП и МП, только защита от такого воздействия сложна. Сведения, которые находятся в таких сформированных полях, иногда очень объемные и не всегда дешифруется. Например, излучение от биологической структуры человека [1].
АПВ-ЭМП. Информационное акустическое поле преобразуется в электрический сигнал, который прямо или после последующих преобразований формируется в электромагнитном поле. Например, акустоэлектрическое преобразование на поверхности.
ВП-ЭМП. Вибрационные колебания модулируют высокочастотные электромагнитные колебания на отражающихся поверхностях. Информация передается электромагнитным полем.
ГАП-ГАП. За счет нелинейности жидкой среды формируются поля и спектры частот, которые содержат сведения о технических средствах. Например, кавитационный спектр, модуляционный спектр и др.
АПВ-АПВ. Формирование и снятие данных за счет взаимодействия акустических волн низких и высоких частот на нелинейных структурах.
Математическая модель физических полей макромира
Математическая модель охватывает класс неопределяемых абстрактных, символических математических объектов, таких как числа или векторы, и отношения между этими объектами.
Под математической моделью понимают количественную формализацию абстрактных представлений об изучаемой системе. Математическая модель это формальное описание системы с помощью математических средств, дифференциальных, интегральных, разностных, алгебраических уравнений, а также неравенств, множеств и т. д.
Рассмотрим математическую модель физических полей макромира (гравитационного, электромагнитного, акустического) (Рис.1), которая характеризует информацию.
Математическая модель гравитационного поля
Математическую модель гравитационного поля представим дифференциальным уравнением гравитационного поля в ньютоновской механике [2].Такое уравнение получаются переходом от закона всемирного тяготения Ньютона, где сила взаимного притяжения двух тел, которые могут быть приняты за материальные точки, прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними, к дифференциальным уравнениям в теории ньютоновского потенциала.
Итак, имеются две материальные точки с массами m и m они притягиваются друг к другу по закону Ньютона и на точку m со стороны точки m действует сила (1.1), где rk – расстояние между точками т и mk, γ – гравитационная постоянная, r – единичный вектор направления от m к m.
Потенциальный характер сил тяготения т. е. Fk = grad Φk, позволяет ввести скалярную характеристику гравитационного поля – потенциал, который для двух материальных точек (1.2).
Если и пространстве имеется n материальных точек с массами m (k = 1, 2,.. п) и рассматривается их влияние на одну материальную точку массы m = 1, которая может быть помещена в разные точки пространства (пробная масса), то со стороны всех точек mk на пробную массу m = 1 будет действовать сила F = ΣFk и ее потенциал (1.3).
Распределение масс mk создает в пространстве гравитационное поле с потенциалом Φ, которое можно обнаружить с помощью пробной массы, помещенной в рассматриваемую точку пространства. Напишем дифференциальное уравнение, которому должен удовлетворять потенциал сил тяготения Φ. [2] Рассмотрим функцию 1 /, где (1.4) – расстояние между точкой х, у, z, в которой помещена пробная масса, и точкой xk, yk, zк, в которой находится k-тая масса, создающая гравитационное поле, является гармонической функцией. Во всех точках х, у, z, для которых rk, функция 1/rk удовлетворяет уравнению Лапласа (1.5).
Следовательно, потенциал Φk гравитационного поля одной материальной точки удовлетворяет уравнению (1.6).

Уравнение Лапласа является линейным уравнением. Потенциал гравитационного поля Φ (х, у, z), создаваемого непрерывным распределением масс по некоторому объему V, на основании (1.3) можно написать в виде (1.7), где ρdV=dm, ρ– плотность распределения массы элемента объема dV, dm-прирост массы.
Эта функция Φ (х, у, r) удовлетворяет уравнению Лапласа Φ (х, у, r) = 0 в точках, где нет масс.
Уравнение Лапласа для Φ равносильно уравнениям (1.8).
Можно показать при весьма общих практически приемлемых допущениях относительно распределения плотности ρ, что потенциал Φ гравитационного поля (1.7) для точек х, у, z, расположенных внутри V, удовлетворяет уравнению Пуассона (1.9).
Уравнение (1.9) равносильно уравнениям (1.10).
Практически приходится обычно иметь дело со слабыми гравитационными полями, для которых уравнения поля линейны. Для таких полей в первом приближении справедлив принцип суперпозиции. Волновое уравнение слабого гравитационного поля можно получить, если добавить вторую производную по времени в уравнение (1.9), превратив уравнение Пауссона в уравнение Д"Аламбера.
Математическая модель акустического поля
Акустика – область физики, исследующая упругие колебания и волны, их взаимодействие с веществом и применение.
Во всех средах (жидких, газообразных и твердых) распространение упругих волн происходит так: частицы среды в волне приобретают скорость, деформируются, и в них возникают упругие напряжения, которые и передают волну дальше.
Акустика жидкостей и газов рассматривается на основе гидродинамики, где возмущения передаются силами давления, которые возникают при сжатии и расширении частиц. В твердых телах возникают еще и поля (сдвиговые) упругих напряжений.
Математическая модель акустического поля представлена полной системой уравнений акустики, которая состоит из уравнений движении, уравнения непрерывности и уравнения состояния. Уравнения акустики кратко можно характеризовать так. [3].
Уравнения Эйлера – уравнения движения частиц под действием сил упругости среды. Рассмотрим частицу среды малого объема, ограниченную поверхностью. Так как частица мала, а характеристики среды непрерывны, можем считать плотность по всей среде постоянной, массу частицы приравнять произведению плотности на объем. Далее, полагая, что вся частица движется как одно целое, найти ее ускорение как производную dv/dt ее скорости v по времени t. Рассмотрим давление p и сторонние cилы F а. ст, действующие на частицу со стороны окружающей среды, – силы давления.
Применяя к частице, находящейся под действием только сил давления, второй закон Ньютона и используя теорему Гаусса – Остроградского заменяя интеграл по поверхности интегралом по объему, а также учитывая непрерывности всех характеристик среды, что позволяет градиент давления на протяжении малой частицы считать постоянным, получить уравнение Эйлера (2.1).
Если помимо сил давления на среду действуют сторонние силы Fа. ст, распределенные с плотностью ρ на единицу объема, то уравнение (2.1) примет вид (2.2).
Уравнение движения среды есть нелинейное векторное уравнение первого порядка относительно характеристик среды р, v, ρ.
Уравнение неразрывности среды. Если в среде не образуется разрывов (как, например, разрывы при кавитации), то уравнение неразрывности применимо к исследуемой среде.
Рассмотрим объем среды, ограниченный неподвижной поверхностью S. Если разрывов нет, то приращение массы в объеме равно массе среды, втекшей через поверхность S. Запишем скорость приращения массы в малом объеме, массу, втекающая за единицу времени через элемент поверхности dS, равную v dS.
Заменяя интеграл по поверхности интегралом по объему, получим уравнение неразрывности в виде (2.3).
Уравнение неразрывности скалярно и, как уравнение Эйлера, нелинейно относительно характеристик среды. В дальнейшем встретятся случаи движения среды, удовлетворяющие вместо уравнения неразрывности уравнению вида (2.4).
Это уравнение можно также интерпретировать как уравнение неразрывности, но примененное к среде, куда поступает «из ниоткуда» дополнительное «стороннее» количество среды. Величину Vст называют плотностью сторонней объемной скорости: она дает дополнительный объем, поступающий за единицу времени в единичный объем.
Уравнение состояния связывает давление, плотность (или сжатие) и температуру среды. Уравнение состояния не имеет какого-либо стандартного вида для всех веществ, наподобие уравнения Эйлера или уравнения неразрывности. В общем виде уравнение можно записать в виде (2.5).
Уравнение состояния также нелинейно.
Если при данном движении среды плотность однозначно связана с давлением (так бывает обычно в акустике), то уравнение состояния можно записать в виде (2.6).
Система уравнений (2.1), (2.3) и (2.5) или (2.6) является полной системой уравнений гидродинамики.
Волновое уравнение. Полная система уравнений гидродинамики это – нелинейные, точные уравнения. В дальнейшем будем пользоваться приближенными уравнениями линейного типа. Исключая все величины, характеризующую волну, кроме давления приведем полную систему уравнений акустики к одному уравнению относительно давления p (2.7).
Это волновое уравнение второго порядка для давления, где с – скорость звука.
Если записать выражение для давления гармонического колебания волн и затем подставить его в волновое уравнение (2.7), то получим волновое уравнения Гельмгольца (2.8).

Математическая модель электромагнитного поля
Математическая модель электромагнитного поля представляет систему уравнений электромагнитного поля в полном виде или систему уравнений Максвелла [4].
Электромагнитное поле характеризуются следующими векторными величинами: E и H – векторы напряженности электрического и магнитного полей, D и B – векторы электрической и магнитной индукции, I и Im – плотность токов электрической и магнитной проводимости, ρ и ρm – плотность электрических и магнитных зарядов.
Дифференциальная форма системы уравнений выглядит (3.1 – 3.7), где – магнитная проницаемость, – диэлектрическая проницаемость, – удельная проводимость
Эти уравнения будут исходными при рассмотрение переменных электромагнитных полей и процессов.
Первое уравнение Максвелла. является дифференциальной формулировкой закона полного тока. Физический смысл 1-го уравнения Максвелла: источниками вихревых магнитных полей являются токи проводимости и токи смещения.
Величина δ в правой части (3.1) есть плотность тока проводимости. Это вектор, указывающий направление движения зарядов.
Законы электромагнетизма – это законы макроскопических процессов, в которых усредняется действие огромных количеств элементарных частиц материи. С точки зрения этих законов, среда представляется сплошной.
Второе уравнение Максвелла (3.2) является дифференциальной формулировкой закона электромагнитной индукции и выражает скорость изменения магнитной индукции В через пространственную производную (rot) напряженности электрического поля Е.
Физический смысл: вихревое электрическое поле создается переменным магнитным полем
Третье уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для электрических полей. Физический смысл: источниками электрического поля (векторов Е и D) являются заряды с плотностью ρ. Дифференциальные уравнения (3.3) показывает, что расходимость электрической индукции равна объемной плотности заряда.
Четвертое уравнение Максвелла является дифференциальной формулировкой теоремы Гаусса для магнитных полей. Физический смысл. Дивергенция вектора В в любой точке пространства равняется нулю, т.е. – источников нет (магнитные заряды в природе отсутствуют). Нет ни стыков, ни источников. Линии магнитной индукции непрерывны.
Из уравнений (3.1) и (3.3) можно прийти к уравнению (3.8).
Это уравнение непрерывности. Закон сохранения заряда.
Уравнения (3.5), (3.6), (3.7) характеризуют связь векторов поля с материальной средой.
Установим волновой характер ЭМП. При распространении ЭМП с конечной скоростью происходит запаздывание его по фазе, результатом чего является волновой характер распространения. Можно записать первые два уравнения Максвелла в комплексной форме и заменить в них индукции B и D напряженностями rot E и rot H и ввести функцию комплексной диэлектрической проницаемости проводящей среды при монохроматическом поле. Затем получится полная система уравнений монохроматического ЭМП с комплексными проницаемостью и напряженностями E и H. Волновой характер ЭМП этого гармонического во времени процесса в области без источников получается, если исключить вектор E или вектор H из в уравнениях (3.1) и (3.2), применив оператор rot и учитывая, что расходимость (div) вектора H = 0.
Для однородной непроводящей среды волновое уравнение переходит в уравнение Гельмголца, которое запишется в уравнения (3.9 – 3.10), где k = ω εμ – волновое число.

Об аналогии описания физических полей
Из рассмотренных математических моделей физических полей микромира видно, что гравитационное, акустическое и электромагнитное поля описываются при определенных условиях волновыми уравнениями (1.9, 2.7, 2.8, 3.9, 3.10). Мы имеем ситуацию, когда различные физические явления (поля) описываются аналогичными дифференциальными и другими уравнениями. То есть между физическими явлениями существует аналогия, которая основывается на сходстве уравнений, лежащих в основе описания данных физических явлений
Аналогия ЭМП и акустического поля.
Например, акустические волны описываются уравнениями Гельмгольца (2.8). Электромагнитные волны описываются уравнениями Максвелла, которые после соответствующих преобразований также переходят в уравнения Гельмгольца для однородной среды (3.9). Т.е. в двумерном случае уравнения Максвелла сводятся к двум независимым уравнениям для векторов напряженности электрического и магнитного полей (4.1 – 4.2).
Такие же уравнения можно записать для каждой из составляющих векторов вдоль осей x, у, z. В результате для каждой составляющей получаем уравнение Гельмгольца. Поэтому в двумерном случае решения акустических и электромагнитных задач совпадают. Однако при сопоставлении решений задач необходимо привести в соответствие и граничные условия. Рассмотрим примеры [5].
При абсолютно мягкой поверхность (для ЭМП-абсолютная проводящая поверхность и для АП—давление на поверхности равно нулю), если электромагнитная волна, падающая на поверхность имеет Е-поляризацию (вектор Е параллелен оси y),решениедля вектора Е полностью переносится на величину звукового давления р для абсолютно мягкой поверхности.
При абсолютно жесткой поверхности решение для вектора H, поляризованного параллельно образующей оси y, переносится на величину звукового давления p для абсолютно жесткой поверхности.
Промежуточный случай для электромагнитных волн, когда векторы E и H не параллельны границам раздела, распадается на два рассмотренных случая.
Задача об отражение звуковых волн от плоской границы раздела двух различных сред аналогична задаче об отражения ЭМВ от плоской границы двух диэлектрических сред. Было получено, что аналогом звукового давления р в рассматриваемой задаче будет Еу, а аналогом нормальной составляющей колебательной скорости Vz – величина Нх. Выражение, определяющее коэффициент отражения для вектора E=Еу, будет аналогично формуле для коэффициента отражения звуковой волны (по давлению).
Для акустических волн сохраняется известный закон преломления в оптическом диапазоне ЭМВ. Сохраняются также другие закономерности.
В трехмерном случае за редким исключением векторные уравнения Максвелла не сводятся к скалярным, и найти решения для электромагнитных волн, которые бы соответствовали и звуковым волнам, невозможно. Однако несоответствие между решениями акустических и электромагнитных задач постепенно уменьшается при увеличении волнового размера тела.
Поэтому все результаты, полученные в теории излучения электромагнитных волн, остаются справедливыми и в акустическом случае.

Аналогия ЭМП и гравитационного поля
В математической модели гравитационное поле описывается уравнениями (1.9 и 1.10). Покажем, что это уравнение аналогично уравнению Максвелла для электростатического поля. Так как задача определения потенциала гравитационного поля и силы, действующей со стороны поля на пробную единичную массу, может быть поставлена как задача об определении функции Φ (х,у,z), исчезающей в бесконечности и удовлетворяющей уравнению Лапласа всюду вне V и уравнению Пуассона всюду внутри V, или как задача определения сил F, удовлетворяющих уравнениям (1.8) и (1.10). Такого рода постановка задачи в теории ньютоновского потенциала полностью аналогична постановке задачи электростатики на основе уравнений Максвелла. Можно показать, что решение в бесконечном пространстве задачи об отыскании функции Φ (х,у,z) исчезающей в бесконечности, приводит к формуле (1.7), выражающей собой закон гравитационного тяготения.
Векторной характеристикой гравитационного поля является его напряженность – силовая характеристика точки поля тяготения, равная отношению силы тяготения F, действующей на помещенную в него материальную точку к массе этой точки m.
Предположение о существовании гравитационных волн есть один из вариантов решения уравнений Эйнштейна.
Существование электромагнитных волн также было результатом одного из возможных решений уравнений Максвелла (переменное движение электрических зарядов и переменные электрические токи являются источниками электромагнитных волн).
Точно также считается, что переменное движение массы приводит к излучению гравитационных волн. В настоящее время гравитационные волны определяют как переменное гравитационное поле, распространяющееся со скоростью света и проявляющееся в возникновении относительных ускорений тел.
Интерпритация модели для реальных объектов защиты информации
На рис.2 представлена реальная картина наличия физических полей, их суперпозиция и взаимодействия для простого объекта информатизации, в качестве которого выбрано автоматизированное рабочее место на базе одного персонального компьютера. Разнообразие параметров физических полей представлено напряженностью электрического поля E, напряженностью магнитного H и электромагнитного E,H полей, частотой f, коэффициентом модуляции, спектром сигнала, напряжением, током и другими параметрами.

Рис. 2 – Картина физических полей, их суперпозиция и взаимодействия для автоматизированного рабочего места на базе одного персонального компьютера
Рис.3 отражает картину акустического поля, его суперпозицию и нелинейные взаимодействия на примере помещения, где циркулирует защищаемые акустические поля. Поле характеризуется такими параметрами: как: частота f, давление P, колебательная скоростьVk, ускорение а, разборчивость речи W и др.

Рис. 3 – Картина акустического поля, его суперпозиция и нелинейные взаимодействия на примере одного помещения
Вывод
1 Введено понятие информации как физическое поле.
2 Показано, что вся информация, сформированная и воспринимаемая – это физическое поле или суперпозиция и взаимодействие полей.
3 Представлена математическая модель физических полей.
4 Показана аналогия описания и изучения физических полей с помощью волновых уравнений.
5 Материал данной работы является исходными данными для реализации модели исследования согласно Рис. 1.