Теорема Виета (краткие теоретические сведения)
Формулировка теоремы Виета:
Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.
Таким образом, если уравнение x2 + bx + c = 0 имеет два корня: x1 и x2, то справедливы следующие два равенства:
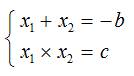
Согласно этим равенствам, для получения решения квадратного уравнения необходимо подбором найти два числа, сумма которых равна коэффициенту при x, взятому с обратным знаком, а произведение равно свободному члену. Следует заметить, что при этом исходное квадратное уравнение должно быть приведено к виду, когда коэффициент a при x2 равен единице.
Доказательство теоремы Виета
Докажем теорему Виета.
Формулы для вычисления корней квадратного уравнения (рассматривается ситуация, когда дискриминант D положителен; уравнение с нулевым дискриминантом можно считать частным случаем):

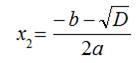
Вычислим сумму этих корней:

Раскрыв скобки и сократив слагаемые, получаем:

.
Вычислим произведение корней:

Применив в числителе формулу разности квадратов, получаем:

Подставляем известную нам формулу для вычисления дискриминанта:

Получаем:

Таким образом, оба равенства теоремы Виета доказаны.
Обратная теорема Виета
Формулировка обратной теоремы Виета:
Если числа x1 и x2 таковы, что их сумма равна второму коэффициенту уравнения x2 + bx + c = 0, взятому с противоположным знаком, а их произведение равно свободному члену, то эти числа являются корнями x2 + bx + c = 0.
Доказательство обратной теоремы Виета читатели могут произвести самостоятельно.