Физика в быту - читать онлайн

Что такое звук?

Мы слышим звук, когда что-то заставляет вибрировать, то есть колебаться, барабанные перепонки в наших ушах. Причём частота вибрации должна лежать в определённых пределах: не менее 16 колебаний в секунду (то есть 16 герц) и не более 20 тысяч колебаний в секунду (20 тысяч герц). Эту область частот называют звуковым диапазоном. Колебания барабанной перепонки с частотой менее 16 герц и более 20 тысяч герц мы не воспринимаем как звук, то есть не слышим. Сразу оговоримся: таков звуковой диапазон для молодых людей. Но уже с 15–20 лет этот диапазон начинает заметно сужаться, особенно со стороны высоких частот. Так что к 35 годам люди перестают слышать звуки с частотой более 15 тысяч герц, а к 50 годам верхний предел снижается, как правило, до 12 тысяч герц (у многих мужчин даже до 6–7 тысяч герц). Причём для того, чтобы предельно низкие и предельно высокие звуки были услышаны, они должны быть очень сильными, то есть вызывающими гораздо более интенсивные колебания барабанных перепонок, чем звуки середины звукового диапазона.

Колебания – это периодически повторяющиеся движения, они характеризуются частотой – числом колебаний в секунду. Частота измеряется в герцах (сокращённо Гц): 1 Гц – это одно колебание в секунду.

Одни звуки мы воспринимаем как низкие (басовые), другие – как высокие, тонкие. Музыканты называют это высотой тона. Именно частота колебаний определяет высоту тона: большая частота создаёт ощущение высокого звука, малая частота – низкого.

Итак, ощущение звука связано с вибрацией барабанных перепонок. Но что её вызывает? Обычно нас окружает воздух. Вибрации воздуха, его периодические сгущения и разрежения – вот что заставляет так же периодически двигаться наши барабанные перепонки. А что порождает вибрации воздуха? Периодические или непериодические изменения плотности окружающей среды создаёт источник звука.

Этим источником может быть любое тело: можно ущипнуть струну или провести по ней смычком, постучать по чему-нибудь, поскрести, потрясти… Нужно, чтобы поверхность тела-источника начала колебаться, колыхаться, дрожать. Положите ладонь на горло во время пения или потрогайте крышку звучащего рояля, и вы почувствуете вибрацию.

Вибрирующая поверхность источника изменяет плотность прилегающего слоя окружающей среды: воздуха или воды, а иногда и твёрдого тела (копыта коня стучат по земле). Все эти среды – газообразная, жидкая, твёрдая – являются упругими, то есть изменения плотности и давления, возникшие в одном месте, передаются от слоя к слою, распространяясь всё дальше от источника, подобно кругам на воде от брошенного камня. Такая передача объясняется взаимодействием молекул среды друг с другом. В газе это взаимодействие сводится к столкновениям молекул: молекулы из места уплотнения расталкивают молекулы в прилегающих слоях, заставляя их так же толкать своих соседей. В итоге колебания плотности и давления передаются от слоя к слою с определённой скоростью – скоростью звука. В газах эта скорость составляет сотни метров в секунду (в воздухе при комнатной температуре она равна 340 м/с). Обратите внимание: при распространении звуковой волны сами массы воздуха не перемещаются, каждая частичка среды лишь колеблется туда-сюда и заставляет это делать соседние частицы.

В жидких и твёрдых средах молекулы «чувствуют» друг друга на расстоянии электрическими полями: стоит одному слою молекул чуть сместиться от своего положения равновесия, как соседние молекулы почувствуют это и тоже придут в движение – начнут колебаться около своих равновесных положений, воздействуя в свою очередь на следующие слои. Поэтому звуковые волны в плотных средах распространяются быстрее, чем в газах. Так, в воде скорость звука около 1,5 км/с, а в твёрдых телах и того больше.

Звуковая волна – это процесс распространения колебаний плотности и давления в упругой среде (воздухе, воде и любом твёрдом веществе).

И вот звуковая волна доходит до барабанной перепонки уха, вызывая её движения. От перепонки колебания через систему слуховых косточек передаются улитке внутреннего уха (мы ещё поговорим о ней в своё время), а от неё уже в виде электрических импульсов по слуховому нерву поступают в нужную зону мозга, который обрабатывает полученный сигнал. И мы слышим звук. Так что звук – явление не только физическое, но и физиологическое.

Ощущение звука возникает в результате воздействия колебаний давления воздуха (или воды, если человек находится в воде) на барабанную перепонку уха.

Итак, чтобы мы услышали звук, необходимы три составляющие:

1. Источник звука, создающий периодические или непериодические изменения плотности частиц окружающей среды.

2. Упругая среда, которая передаёт возникшие в ней уплотнения во все стороны.

3. Приёмник звука (барабанные перепонки и весь наш слуховой аппарат). Добавим сюда и мозг, обрабатывающий сигналы от звуковых нервов.

Неслышные звуки

Звуковые волны с частотой менее 16 Гц называют инфразвуком, а с частотой более 20 000 Гц – ультразвуком. Мы не воспринимаем такие колебания барабанной перепонки как звук, но значит ли это, что мы совсем их не чувствуем?

Исследования инфразвука начались в середине прошлого века. Инфразвук появляется при землетрясениях, цунами, ударах грома, вибрациях тяжелых станков, рёве реактивных двигателей.

Он присутствует и в рок-музыке, особенно в тяжёлом роке и на «живых» концертах.

Инфразвуковые волны проходят сквозь любые преграды и распространяются на огромные расстояния.

У многих морских животных развита чувствительность к инфразвуку, благодаря которой они узнают о приближении шторма. Некоторые виды наземных животных (в том числе кошки) изменяют своё поведение перед землетрясением.

Что позволяет им чувствовать его приближение? Малые колебания грунта, увеличение статического электричества, воздействие инфразвуковых волн? Точно неизвестно. Возможно, все факторы вместе. А тигры, слоны, аллигаторы просто слышат инфразвук и даже могут общаться с его помощью!

Хотя человеку и большинству животных инфразвук и не слышен, он всё же действует на внутренние органы и системы организма и вызывает чувство тревоги. Этот эффект пытались использовать в фильмах ужасов, но потом запретили, так как инфразвук может привести к неконтролируемой панике среди зрителей. При большой интенсивности инфразвук ощущается как вибрация в теле, вызывая недомогания (тошноту, головокружение, вялость) и даже чувство острой боли. Наиболее негативное влияние инфразвук оказывает на нервную систему и работу сердца. Есть предположение, что инфразвук, возникающий от шторма в океане, увеличивает число автокатастроф и сердечных заболеваний на расстояниях в тысячи километров!

Инфразвук при длительном воздействии вызывает состояние усталости. Присутствием инфразвука в шумах автострад и рёве взлетающих самолётов может объясняться синдром усталости у живущих поблизости людей.

Ультразвук имеет частоты, превышающие верхний порог звукового диапазона, то есть выше 20 тысяч (а для пожилых людей – выше 12 тысяч) герц.

Многие животные могут воспринимать ультразвук, например кошки, собаки, кузнечики, летучие мыши, бабочки. Дельфины и другие морские животные для поисков косяков рыб, для ориентировки в мутной воде используют ультразвуковую локацию, то есть посылают ультразвуковой сигнал, а затем ловят сигнал, отражённый от препятствия. По времени запаздывания отраженного сигнала они судят о расстоянии до препятствия, а по изменению частоты сигнала – о скорости движения этого препятствия (этот же принцип применяют «гаишники» для определения скорости вашего автомобиля). Почему дельфины предпочитают зрению ультразвуковую локацию? Потому что свет в воде довольно сильно поглощается (радиус видимости составляет несколько метров), а ультразвук с частотой 50 тысяч герц распространяется на несколько километров! Летучие мыши и другие ночные животные благодаря ультразвуковой локации ориентируются при ночном полёте. В медицине тоже широко применяется ультразвуковая локация – это знакомая вам процедура УЗИ.

Как измеряют волны

Поговорим немного подробнее о волнах. Это пригодится нам не только в связи со звуком, но и при разговоре об электромагнитном излучении и свете.

Чтобы нагляднее представить себе звуковую волну, воспользуемся аналогией. Характер движения частиц среды в бегущей волне напоминает работу «семафорного телеграфа», применявшегося в конце XVIII – начале XIX века. Между городами в области прямой видимости возводили специальные башни с мачтами. К концу мачты прикреплялись подвижные линейки, которые могли принимать различные положения, изображая таким образом все буквы и даже некоторые слова. Работник на каждой башне наблюдал за соседней башней в подзорную трубу и воспроизводил на своей мачте те же самые движения линеек, которые совершал его предшественник, но с небольшой задержкой во времени.

И так сигнал «бежал» от башни к башне. От Парижа до Бреста депеша передавалась всего за 7 минут! Так и в бегущей звуковой волне частицы в каждой точке среды повторяют те же самые движения, которые совершают частицы «на первой башне», то есть движения источника звука, но с некоторым запаздыванием, время которого определяется расстоянием до источника и скоростью волны.

Рис. 1. Пример графика зависимости смещений частиц среды от своих равновесных положений в один и тот же момент времени в зависимости от расстояния до источника звука

Если движения источника звука периодические, то такими же будут и движения частиц среды, причём частицы, находящиеся на определённом расстоянии друг от друга (в направлении распространения волны), будут совершать синхронные движения. Такое минимальное расстояние называется длиной волны. Если в какой-то момент времени мы сделаем «мгновенную фотографию» распределения смещений частиц от своих равновесных положений, то увидим повторяющуюся картину (рис. 1).

Итак, длина волны – это минимальное расстояние между частицами среды, колеблющимися синхронно. Длина волны связана с частотой колебаний: чем больше частота, тем меньше в данной среде длина волны. Запомним это!

Длина волны λ равна расстоянию, на которое распространяется волна за время, равное периоду колебаний Т. Если v – скорость распространения волны, то λ = v·T. Частота колебаний f – это величина, обратная периоду:

f = 1/T , поэтому λ = v/f.

Чем больше скорость волны и чем больше период колебаний (то есть меньше частота), тем больше длина волны. Эта формула справедлива для любых волн, как звуковых, так и электромагнитных. Мы ещё не раз её вспомним.

Инфразвуковые низкочастотные волны самые длинные: в воздухе более 20 м и могут достигать сотен метров. Длины волн для ультразвука, наоборот, очень малы: в воздухе менее 15 мм. При ультразвуковой диагностике в медицине применяют волны длиной в доли миллиметра – именно такие короткие волны позволяют заметить в тканях организма неоднородности малого размера (ведь волны любой природы не замечают преград, размер которых гораздо меньше длины волны – так, океанская волна «не заметит» маленький камушек на своём пути). Столь же короткие ультразвуковые волны используют летучие мыши для локации. Ну а для звукового диапазона длины волн в воздухе простираются от 15 мм до 20 метров.

Обратите внимание: длина волны изменяется при переходе волны из одной среды в другую. Так, в воде или другой среде все длины волн уменьшаются во столько же раз, во сколько раз увеличивается скорость звука (в воде – в 4,4 раза).

Частота же колебаний частиц в волне – это её неизменяющаяся характеристика. Поэтому физики предпочитают характеризовать волну именно частотой колебаний частиц.

Рис. 2. Смещение частицы среды как функция времени в гармонической волне

Ещё одна важная характеристика волны – её интенсивность. Она определяется амплитудой («размахом») колебаний частиц в волне и связана с громкостью воспринимаемого звука (позже поговорим об этом подробнее).

Наконец, очень важна форма колебаний. Мы имеем в виду форму графика, изображающего зависимость смещения частиц среды в фиксированном месте от времени. Такая же форма повторится на «мгновенной фотографии» распределения смещений частиц среды вдоль направления распространения волны (рис. 1). Наиболее простая форма колебаний – синусоидальная (рис. 2). Волны с такой формой колебаний называют гармоническими. Они имеют очень большое значение в акустике и вообще в физике. Вскоре мы узнаем почему.

Секреты музыкальных звуков

Внимание! Сейчас мы откроем тайну музыкальных и немузыкальных звуков. Итак: любые периодические колебания источника рождают музыкальный звук, а непериодические – немузыкальный.

Музыкальный звук мы можем пропеть, немузыкальный – не можем. У музыкальных звуков мы различаем высоту тона (то есть отождествляем звук с определённой нотой музыкального строя), у немузыкальных – нет. К примеру, пение птиц красиво, но записать его нотами и воспроизвести голосом или на музыкальном инструменте не получается (разве что «ку-ку» можно спеть вполне узнаваемо).

Ещё у музыкальных звуков есть тембр – «звуковой окрас», позволяющий отличить ноту «до», взятую на рояле, от такой же ноты, взятой на другом инструменте.

Где же в форме колебаний спрятаны все эти особенности музыкального звука? И как можно классифицировать многообразие всевозможных форм колебаний, чтобы можно было «подделывать» (синтезировать) нужные звуки или сделать программы их распознавания?

Рис. 3. Пример разложения периодического колебания (кривая 3) на гармоники (кривые 1 и 2)

Оказывается, любое периодическое движение чисто математически может быть представлено как сумма гармонических колебаний с кратными частотами, то есть с частотами, полученными умножением некоторой основной частоты f₀ на целые числа: 2, 3, 4… (это известная математикам теорема Фурье). Наименьшая частота этого ряда (f₀) называется основной, а колебание с этой частотой – основным колебанием или первой гармоникой. Основная частота определяется периодом исходного движения. Колебания с кратными частотами 2f₀, 3f₀, 4f₀… называют гармоническими обертонами или просто гармониками (второй, третьей, четвёртой и так далее до бесконечности). Многообразие сочетаний различных амплитуд (и фаз) гармоник обеспечивает все возможные формы результирующего колебания.

Процедура выделения простых гармоник из сложного колебания называется спектральным (или гармоническим) анализом. На рисунке 3 приведён пример разложения колебания на гармоники (в данном примере понадобилось всего две гармоники с частотами f₀ и 2f₀). Такой анализ можно произвести математически, а можно разложить звук на гармоники с помощью прибора – спектроанализатора.

Нарисуем график, состоящий из вертикальных отрезков: высоты отрезков соответствуют амплитудам гармоник, их положение на горизонтальной оси – частотам. Такая картинка изображает спектр колебания (спектр звука). Итак, спектр звука показывает, гармоники (обертоны) каких частот и с какими амплитудами присутствуют в данном звуке.

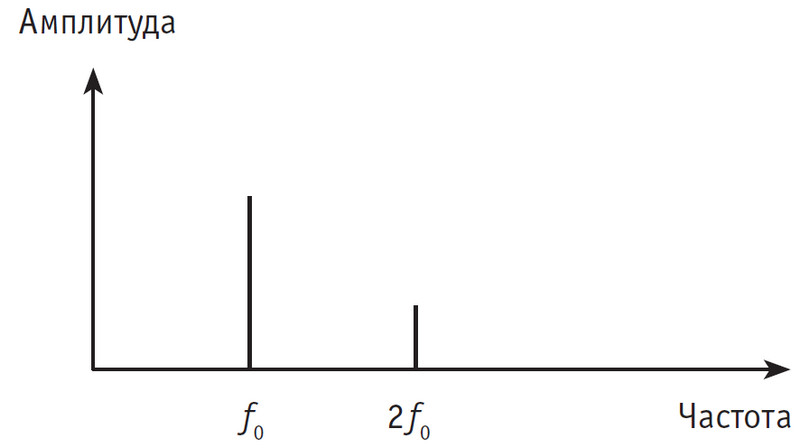
Рис. 4. Спектр колебания, представленного на рис. 3

Основная частота определяет высоту тона, а все остальные (высшие) гармоники создают неповторимый тембр звука.

Основная частота для самого низкого мужского голоса (бас) составляет 80 Гц. Основная частота для самого высокого женского голоса (сопрано) достигает 1050 Гц. Обертоны же могут простираться до частот порядка 50 тысяч герц, выходя за пределы частотного диапазона слухового восприятия.

Основная частота звуков, издаваемых музыкальными инструментами, лежит в диапазоне 40–5000 Гц.

Нота «ля» первой октавы имеет частоту 440 Гц.

Как правило, первая гармоника (основная частота) присутствует в музыкальном звуке с наибольшей амплитудой. Но это не обязательно так. В спектре флейты, фагота, корнета и трубы некоторые высшие гармоники столь же сильны, как и основная частота, или даже сильнее. Но ухо не проведёшь! Оно безошибочно распознаёт основную частоту, даже если её вовсе нет в спектре, а присутствуют лишь гармоники 2f₀, 3f₀, 4f₀,… Так, например, музыкальный звук, состоящий из набора частот 200, 300, 400 и 500 Гц, воспринимается как звук высотой 100 Гц, хотя этой частоты нет в наборе. Другими словами, мы слышим отсутствующий звук! Это связано с особенностями человеческого уха, которое вносит свои искажения. Так, при возбуждении его двумя частотами f₁ и f₂ в нём возбуждаются также суммарная и разностная частоты f₁+f₂ и f₁−f₂ вместе со всеми их гармониками. Чем больше амплитуда исходных колебаний, тем больше слышны «лишние» частоты – их называют субъективными тонами. В нашем примере, когда в спектре объективно присутствуют частоты 200, 300, 400 и 500 Гц, но нет основного тона 100 Гц, в ухе возникают колебания разностных частот 300–200=100 (Гц), 400–300=100 (Гц) и т. д., то есть колебания отсутствующего основного тона. Для любого музыкального звука основная частота эффективно усиливается разностными частотами и обязательно будет опознана ухом.

Бесконечное разнообразие спектров музыкальных звуков, то есть сочетаний частот и амплитуд гармоник, объясняет разнообразие тембров звучания. В природе не существует «простых» звуков, тембрально не окрашенных (состоящих только из колебаний одного основного тона). Такой звук можно искусственно синтезировать, преобразовав электромагнитное колебание одной частоты в звуковое с помощью так называемого звукового генератора, причём ухо воспринимает этот звук как весьма противный. Более того, человеку труднее опознать высоту тона «чистого» звука, чем звука с тембральным окрасом, и мы уже поняли почему. Из инструментальных звуков наиболее «чистым», почти без примеси гармоник, является звук камертона.

Если в звуке много гармоник, то он воспринимается «богатым». Так, в спектре голоса хорошего оперного певца гораздо больше обертонов, чем в спектре любителя, поющего ту же арию.

Но если в спектре слишком много гармоник, то звук кажется «грязным», а если там много верхних гармоник – то и резким, крикливым, неприятным.

Тембр детских звучащих книжек очень бедный. Он «урезан» буквально до одной-двух гармоник. Такие книжки портят слух.

Подумаем: почему низкие звуки на рояле звучат «богато» (рояль рокочет), а верхние звуки – «бедненько»? Ответ прост. Ухо немолодого человека не слышит гармоники с частотами выше 12–15 тысяч герц. Значит, высшие гармоники высоких звуков просто не воспринимаются. Верхние ноты рояля не виноваты, виноваты наши уши.

А чем можно объяснить пристрастие многих меломанов к громкой музыке? Легко сообразить, что она тембрально богаче: ведь для того, чтобы мы могли слышать высокие обертоны, они должны быть достаточно интенсивными (вспомним, что чувствительность уха быстро падает по мере приближения к границам звукового диапазона). Правда, увеличение громкости имеет смысл, только если вы используете качественную звуковую систему, не обрезающую высшие гармоники.

Слушая современные реставрированные перезаписи голосов великих певцов прошлого, удивляешься: что же такого удивительного люди в них находили? А дело в том, что при реставрации вместе с шумами старой грамзаписи удаляются и многие обертоны – и голос лишается своего волшебства.

Что за шум, что за рёв

Непериодические движения рождают немузыкальные звуки и шумы. Некоторые немузыкальные звуки вполне красивы, например звон колоколов и пение птиц. А другие воспринимаются как шум и рёв. Почему?

Немузыкальный звук тоже имеет свой спектр, но этот спектр уже не является набором обертонов с частотами, кратными наименьшей основной частоте. Он может содержать или «хаотичный» набор отдельных частот, или вообще все частоты в некотором диапазоне (такой спектр называют непрерывным).

Посмотрим, например, на спектр звука колокола. Хотя звон колокола похож на музыкальный звук, подобрать соответствующую ему ноту звукоряда сложно, и как ни пытались композиторы изобразить перезвон колоколов на рояле или с помощью оркестра, узнаваемым оставался скорее ритмический рисунок перезвона, нежели само звучание колоколов. А почему? Спектр звучания колокола представляет собой ряд обертонов, но их частоты не кратны наименьшей частоте. Воспринимаемая высота тона колокола определяется не наименьшей частотой, как для музыкальных звуков, а обертоном, доминирующим сразу после удара. Спустя некоторое время в звуке колокола начинают преобладать более низкие обертоны, и восприятие тона меняется. И если спектры всех роялей в основном похожи друг на друга, то спектры звуков колоколов совершенно индивидуальны.

Звуки с непрерывным спектром воспринимаются как шумы. Если полоса частот не слишком широка, мы можем грубо оценить высоту звука: рычание тигра – низкий звук (полоса низких частот), крик павлина – высокий. Если частоты более-менее равномерно распределены по всему звуковому диапазону, получается так называемый белый шум (пример: рёв близкого водопада).

Пение птиц ещё труднее передать звуками музыки, чем звучание колоколов, хотя шумом его тоже не назовёшь. С точки зрения спектра, это нечто промежуточное между звоном колокола и шумом. Каждая «нота» птичьего пения содержит не ряд кратных частот, как музыкальный звук, и не набор отдельных обертонов, как звук колокола, а несколько узких непрерывных полос частот, причем эти полосы во время песни «ползут» вверх или вниз по шкале частот, совершают резкие взлёты и падения. Именно эти взлёты и падения при переводе птичьего пения на язык музыки композиторы имитируют скачками на те или иные интервалы.

Частоты некоторых птичьих голосов простираются до 50 тысяч герц, уходя в область ультразвука, так что мы слышим лишь часть их песен.

Очень короткие звуки (стук в дверь, хлопок в ладоши) также воспринимаются как немузыкальные. Ведь нашему слуховому аппарату требуется некоторое время для определения периода колебаний и частоты основного тона, а при коротких звуках он просто не успевает это сделать. Спектры коротких звуков непрерывны, как и спектры шумов. Если ширина полосы частот невелика, мы можем приблизительно определить высоту тона, особенно в сравнении с другими подобными звуками. Вспомните, например, детский деревянный ксилофон, состоящий из дощечек разной длины. Удар по одной дощечке воспринимается просто как стук (немузыкальный звук), но ударяя по ряду дощечек-клавиш, мы уже слышим гамму.

Как создать музыкальный звук?

Одни предметы издают музыкальные звуки, а другие – немузыкальные. Самый простой, известный с древних времён источник музыкальных звуков – натянутая струна. Именно с изучения звучания струн началась математическая теория музыки, и основы её заложил в Древней Греции Пифагор (570–490 гг. до н. э.).

Самые простые движения, которые могут совершать точки струны, изображены схематически на рисунке 5: каждая точка движется туда-сюда, словно маятник, в результате струна изгибается так, что её форма соответствует части синусоиды. Длина полного периода такой синусоиды равна длине волны. Если оба конца струны закреплены, то на длине струны укладывается целое число полуволн (на верхнем рисунке – одна полуволна, на среднем – две, на нижнем – три). Такие колебания струны называются стоячими волнами или собственными колебаниями. Частоты этих колебаний кратны друг другу. Если одной полуволне соответствует частота f₀, то частоты колебаний для более коротких волн равны 2f₀ и 3f₀. Как вы понимаете, возможны также колебания с частотами 4f₀, 5f₀ и так далее. Частота f₀ является основной, а все остальные – обертонами или высшими гармониками.

Самое интересное: если вы просто ущипнёте струну, то многие обертоны возбудятся одновременно, и соответствующие им движения наложатся друг на друга, в результате форма струны в процессе колебаний будет уже не синусоидальной, а более сложной. Это как «спектральный анализ наоборот»: сложение простых гармоник даёт в результате сложное колебание.

Ущипнув струну, мы услышим музыкальный звук, высота тона которого соответствует основной частоте f₀, а наличие обертонов придаст звуку тембральный окрас. Щипая струну в разных местах, мы меняем амплитуды обертонов и, значит, меняем тембр. Например, щипок ровно посередине струны исключает из движений чётные гармоники 2f₀, 4f₀ и т. д., так как для этих гармоник средняя точка струны должна быть неподвижна.

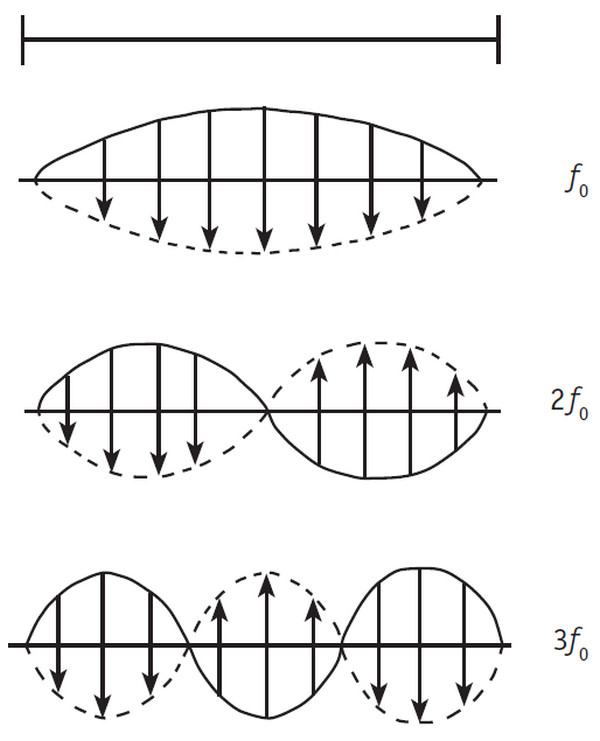
Рис. 5. Простейшие колебания струны (первая, вторая и третья гармоники)

Какими параметрами струны определяется её основная частота? Как видно из рисунка 5, чем длиннее струна, тем больше длина волны первой гармоники, а значит, частота колебаний меньше (низким звукам рояля соответствуют самые длинные струны, высоким – самые короткие). Основная частота f₀ зависит также от натяжения струны: увеличивая натяжение, мы увеличиваем основную частоту (именно путём изменения натяжения струн настройщик добивается нужной частоты звука).

Как и для бегущих волн, длина стоячей волны λ связана с частотой колебаний частиц и скоростью v распространения волны универсальной формулой λ = v/f. Длина волны первой (основной) гармоники, как видно из рисунка 5, в два раза больше длины l струны: λ = 2l. Так что основная частота струны f₀ = v/λ = v/2l. Увеличение натяжения струны приводит к увеличению скорости волн v, а значит, и к увеличению основной частоты.

Ещё одним простым телом, рождающим музыкальные звуки, являются цилиндрические трубы, ширина которых гораздо меньше длины (вспомним, например, трубы оргáна). Главным звучащим телом в трубах является наполняющий их воздух. Возбуждая на одном конце трубы движение воздуха с помощью вибратора, мы приводим в колебательное движение весь столб воздуха в трубе, и он рождает звуковую волну, бегущую от трубы к вашему уху. Основная частота f₀ определяется длиной воздушного столба: чем длиннее труба, тем ниже её звук, как и для струны. И также наряду с основной частотой возбуждаются обертоны с кратными частотами.

Струны и воздушные трубы – основа всех музыкальных инструментов. Именно они рождают музыкальные звуки. Предметы же более сложных форм являются источниками немузыкальных звуков.

Можно ли увидеть звук?

Любой твёрдый предмет будет издавать те или иные звуки, если по нему ударять или, к примеру, водить по нему смычком. И у любого предмета конечных размеров, как и у струн, есть характерный набор собственных колебаний – возможных простейших движений его частиц. У большинства объемных тел частоты собственных колебаний образуют непрерывный спектр в пределах определённой полосы частот, зачастую весьма широкой, то есть воспринимаются ухом как шум. Например, ударив по столу, вы слышите звук, создаваемый возникающими колебаниями стола, но высоту тона определить не можете. Можно только предсказать, что шум от удара по массивному шкафу будет более низкочастотным, чем от удара по небольшому столику.

Немецкий физик и музыкант Эрнест Хладни сумел сделать видимыми собственные колебания плоских пластин разной формы (круглых, квадратных и прочих). Для этого он возбуждал в них колебания с помощью скрипичного смычка (рис. 6). При этом пластины издавали немузыкальные звуки разной степени «противности». На поверхность пластин он насыпал мелкий песок, который слетал с активно колеблющихся областей и концентрировался в тех местах, которые оставались практически неподвижными. Проводя смычком по краю пластины в разных местах, под разными углами и с различной скоростью, можно возбуждать различные собственные колебания и получать самые разные картины: иногда простые, иногда сложные, иногда красивые, иногда беспорядочные. Каждому типу колебаний соответствуют определённая «песочная картина» и своё неповторимое звучание.

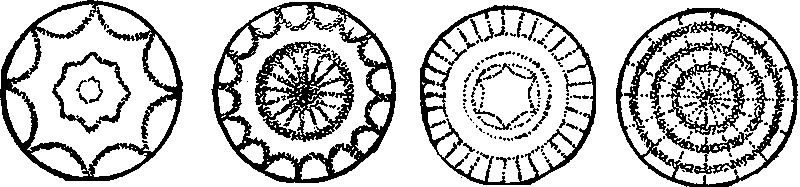
Рис. 6. Примеры фигур Хладни, полученных с помощью насыпанного на поверхность колеблющихся пластин песка

Резонанс и резонаторы

Но вернёмся к музыкальным звукам и струнам. Остаётся вопрос: почему тембры разных струнных инструментов (рояля, скрипки, виолончели и прочих) столь отличаются друг от друга, хотя струны везде практически одинаковые? Всё дело в резонаторах. Давайте разберёмся, что это такое.

До сих пор мы говорили о собственных колебаниях тел – таких колебаниях, которые они совершают «по своему сценарию», стоит только вывести их из равновесия, сообщив запас энергии (ущипнуть струну, постучать по столу, ударить по металлической пластинке, провести смычком и т. д.). Как мы уже знаем, собственные колебания происходят с собственными частотами – с любой из них или одновременно со многими. А что будет, если мы будем извне «навязывать» упругому телу колебания с какой-то частотой? Возникнут колебания, которые называют вынужденными.

Попробуйте закрепить один конец длинного шнура (желательно эластичного), а другой конец периодически раскачивать рукой. По шнуру побежит какая-то рябь. Но постарайтесь подобрать такую частоту качаний, чтобы на длине шнура уложилась одна или несколько полуволн (как на рисунке 5) – шнур отзовётся колебанием значительной амплитуды. Мы наблюдаем при этом явление резонанса – резкое возрастание амплитуды вынужденных колебаний при совпадении частоты вынуждающего периодического воздействия с любой из собственных частот.

Говорят, что Карузо мог разбить бокал голосом, взяв ноту надлежащей высоты. В середине XIX века во Франции рухнул мост, по которому проходил отряд солдат. В Петербурге в XIX веке таким же образом обрушился Египетский мост (с тех пор солдатам запрещено ходить по мостам в ногу). Это всё примеры проявления резонанса.

Слово «резонанс» происходит от французского resonance – звучать, откликаться.