Часть 1 Механика Силы и движение
1. Основы механики
Как мы видели, вся классическая физика представляет собой сочетание двух сил – силы тяготения и электромагнитной силы. Поэтому будет естественным для начала объяснить, что такое сила, и определить, как она влияет на движение тел. Для этого нам нужно заглянуть в историю и поинтересоваться механикой, сначала с Галилеем, затем с Ньютоном.
1. Относительность движения
Необходимость ориентиров для описания движения
Зададим риторический вопрос: что такое движение? Мы видим объекты, которые движутся по отношению к нам (машины, пешеходы…), мы сами перемещаемся по отношению к дороге, к тротуару… «По отношению к» – ключевые слова для описания движения.
Если мы сидим рядом со спящим пассажиром в поезде, он по отношению к нам не движется; однако он движется по отношению к пейзажу, пролетающему за окном. Таким образом, необходим ориентир, чтобы уточнить, по отношению к чему движется объект. В физике подобный ориентир называется системой отсчета, которая является важнейшим понятием.
В предыдущем примере спящий пассажир движется в системе отсчета луга, находящегося снаружи («он движется по отношению к лугу»), но в системе отсчета поезда он не движется («по отношению к поезду пассажир неподвижен»). Если наша цель изучить движение пассажира по отношению к поезду, то мы перемещаемся в систему отсчета поезда. Если наша цель – узнать, когда мы прибудем к месту назначения, необходимо рассмотреть нашу скорость во внешней системе отсчета, то есть луга или просто земной поверхности.
Необходимо запомнить, что выражение «в системе отсчета» является синонимом «по отношению к». По своей природе объект всегда неподвижен в собственной системе отчета: то есть поезд не движется по отношению к поезду.
Земная и геоцентрическая системы отсчета
В повседневной жизни нас чаще всего интересует движение по отношению к земле. Под словом «земля» имеется в виду «земная поверхность». Система отсчета земли, которая кажется нам такой неподвижной, называется «земной системой отсчета», и, по всей вероятности, она является самой главной из всех. Однако она не является абсолютной: Земля вращается вокруг собственной оси, а вместе с ней и ее поверхность… Таким образом, даже будучи неподвижным по отношению к земной поверхности, человек на экваторе преодолевает не менее 40 000 км (окружность Земли) в космосе за один день!
Система отсчета, в которой мы обладаем такой колоссальной скоростью, называется «геоцентрической системой отсчета» (центром является Земля). То есть в земной системе отсчета дом неподвижен, но в геоцентрической системе отсчета он вращается вместе с Землей.
Взгляните на ночное небо: в течение ночи звезды на небе перемещаются. Они движутся по отношению к нам, то есть в земной системе отсчета. Но каждый знает, что их движение связано с вращением Земли: в геоцентрической системе отсчета звезды остаются неподвижны, это мы под ними перемещаемся[2].
Две точки зрения абсолютно идентичны: в повседневной жизни мы наверняка предпочтем считать, что звезды движутся по небу, потому что с нашей точки зрения мы видим это движение (согласно земной системе отсчета). Но космонавт, прилетевший на Марс, увидит, как Земля вращается в космосе, в то время как звезды покажутся ему неподвижными: он предпочтет геоцентрическую систему отсчета.
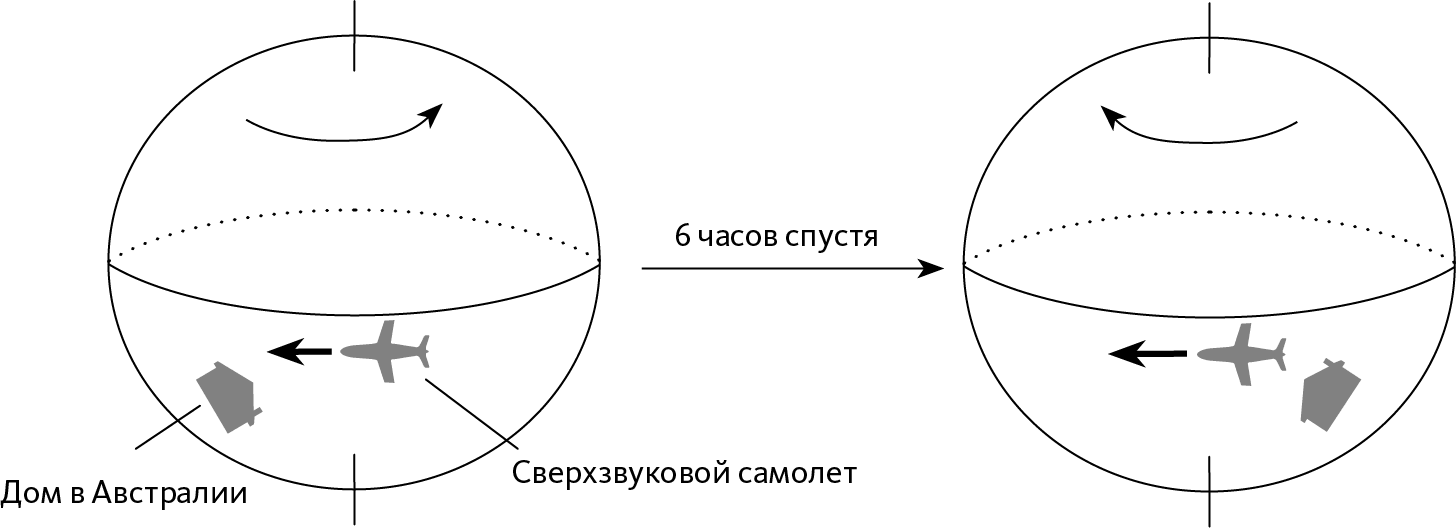
Рис. 1.1 – Движение дома и сверхзвукового самолета
Перед нами дом в Австралии на Земле и сверхзвуковой самолет, который движется на запад. Через 6 часов самолет, который был на востоке Австралии, окажется на западе Австралии.
Для космонавта, который наблюдает вращение Земли из космоса, в геоцентрической системе отсчета дом за 6 часов переместится, а самолет останется неподвижным. Разумеется, по отношению к земной поверхности (земная система отсчета) самолет переместился на запад, а дом остался неподвижным.
Возьмем в качестве примера сверхзвуковой самолет, летящий на запад, чья скорость равна скорости вращения Земли. С точки зрения космонавта самолет неподвижен, а Земля вращается под ним. Однако для человека на Земле самолет перемещается с огромной скоростью (➙ рис. 1.1)…
Гелиоцентрическая система отсчета
Теперь поговорим о Солнце. Из-за вращения Земли кажется, что Солнце проходит по небу за 24 часа. Но не следует забывать, что Земля вращается еще и вокруг Солнца. Это составляет целый комплекс движений, которые к тому же зависят от разных систем отсчета!
Переместимся в горячую точку и представим себя на месте Солнца: Земля делает оборот вокруг нас за один год. Мы находимся в «гелиоцентрической системе отсчета» (Солнце расположено в центре). Однако с точки зрения геоцентрической системы отсчета Земля не перемещается, а лишь вращается вокруг своей оси, а вот Солнце как будто делает круг за 365 дней (➙ рис. 1.2).
В конце концов, древнее представление о том, что Солнце вращается вокруг Земли, вероятно, не так уж неверно… с определенной точки зрения! В дальнейшем мы увидим, почему представление Коперника, несмотря ни на что, было обоснованным.

Рис. 1.2 – Движение Земли и Солнца
С точки зрения космонавта, наблюдающего Солнечную систему со стороны, Земля вращается вокруг неподвижного Солнца (гелиоцентрическая система отсчета).
Человек на Земле видит, что Солнце, находившееся в созвездии Тельца, через три месяца переместилось в созвездие Льва: с точки зрения геоцентрической системы отсчета именно Солнце движется по отношению к звездам.
Мы могли бы продолжить путешествие по Вселенной и рассмотреть мир с точки зрения «галактикоцентрической» системы отсчета: по отношению к центру Галактики наша скорость просто феноменальна, поскольку Земля вращает нас со скоростью 0,5 км/с, вокруг Солнца со скоростью 30 км/с, а в составе Солнечной системы мы делает виток вокруг центра Галактики со скоростью 217 км/c: то есть мы в среднем преодолеваем 217 километров каждую секунду!
Завершим на этом наше космическое путешествие. Благодаря ему мы познакомились с тремя системами отсчета: земной, геоцентрической и гелиоцентрической. Таких систем мы можем найти бесконечное множество: например, поезд или галактика… Однако чаще всего мы будем использовать земную систему отсчета.

А ЧТО ЖЕ АРИСТОТЕЛЬ?
Мы оставили Аристотеля, испуганного перспективой быть расплющенным о спинку сиденья транспортного средства, движущегося со скоростью 50 км/ч. Но что же мы только что узнали? Что наша скорость 217 км/с, или 30 км/с, или 0,5 км/с, или же 0 км/с (в галактикоцентрической, гелиоцентрической, геоцентрической и земной системах отсчета соответственно).
Таким образом, становится ясно, что скорость не является ключевым параметром в понятии силы.

ВЫВОД: ТРИ ВАЖНЫЕ СИСТЕМЫ ОТСЧЕТА
• Земная система отсчета: поверхность Земли неподвижна. Солнце, Луна и звезды вращаются на небе. Такова наиболее распространенная точка зрения.
• Геоцентрическая система отсчета: Земля вращается вокруг своей оси, но не перемещается. Звезды неподвижны (на первый взгляд), но Солнце перемещается по небесному своду.
• Гелиоцентрическая система отсчета: Солнце не перемещается, а лишь вращается вокруг собственной оси. Земля делает виток вокруг Солнца и вращается вокруг своей оси. Звезды кажутся неподвижными (на первый взгляд).
В первую очередь необходимо запомнить, что понятие движения и скорости связаны с системой отсчета: они относительны и имеют смысл только по отношению к какому-либо ориентиру.
Движение изолированного объекта
В предыдущем параграфе мы увидели, что, по всей видимости, абсолютной системы отсчета не существует: все точки зрения справедливы.
Это мы установили на примере движения сверхзвукового самолета, летящего на запад, противопоставленного вращению Земли: человек на Земле (земная система отсчета) видит самолет, летящий с большой скоростью. Человек в космосе (геоцентрическая система отсчета) видит, что самолет неподвижен, а Земля вращается. Оба человека правы.
Однако две эти системы отсчета не равнозначны для всех точек зрения, и именно это мы попытаемся продемонстрировать ниже.
Первопроходцем в этой области был Галилей. Ему пришла в голову следующая мысль: каким будет движение одиночного объекта при отсутствии какого-либо окружения в зависимости от определенной системы отсчета?
Подобный одиночный объект называется изолированным. Проблема в том, что полностью изолированных предметов, с которыми можно было бы провести опыт, не существует, тем более на Земле! Как бы там ни было, Галилей попытался провести такой опыт, постаравшись максимально снизить влияние окружающей среды. Например, повинуясь земному притяжению, шарик мог бы упасть еще ниже, но его задерживает поверхность земли: эти два условия компенсируют друг друга, и объект называется псевдоизолированным.
Но что же произойдет, если покатить шарик по земле?
• Первый факт: шарик катится все время прямо, его траектория по отношению к земной поверхности прямолинейна.
• Второй факт: его скорость не уменьшается, по крайней мере если достаточно снизить сопротивление воздуха (необходимое условие для псевдоизолированного объекта). Такую скорость называют равномерной, она остается постоянной по отношению к земной поверхности.
Таким образом, естественному движению изолированного объекта в земной системе отсчета свойственна «равномерная прямолинейная» траектория.
Действительно, если наша машина поворачивает налево, нас прижимает к правой дверце, потому что наше тело «хочет» двигаться прямо, а машина нам в этом мешает (➙ рис. 1.3).
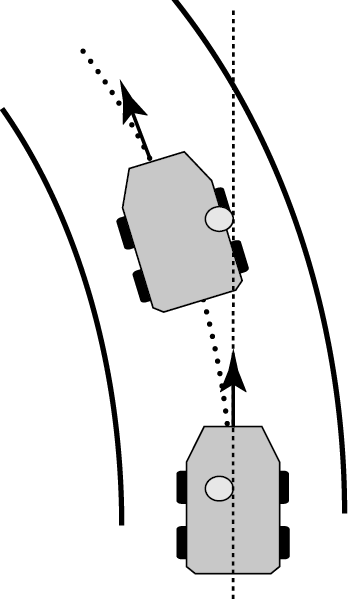
Рис. 1.3 – Машина поворачивает влево
На рисунке представлены положения машины до и после поворота. Тело человека, находящегося внутри (кружок), следует по прямолинейной равномерной траектории (пунктирная прямая) и оказывается прижатым к правой дверце.
Когда машина тормозит, наше тело наклоняется вперед, потому что мы не «хотим» терять равномерную скорость, с которой двигались (➙ рис. 1.4). В любом случае наше тело стремится сохранить прямолинейную равномерную траекторию.

Рис. 1.4 – Машина в момент торможения
На рисунке представлены три положения машины в течение одной секунды. Между 2-й и 3-й позицией машина начала тормозить. Но тело человека, сидящего внутри (кружок), стремится сохранить прямолинейную равномерную траекторию, поэтому человек оказался прижатым к лобовому стеклу.
Очень необычная система отсчета
Выйдем из машины и положим мяч на горизонтальную земную поверхность: он останется лежать неподвижно там, куда его положили. На самом деле это частный случай «прямолинейной равномерной траектории», о которой уже говорилось раньше: слово «равномерный» означает, что скорость остается постоянной. А если скорость нулевая, она останется нулевой…
Проблема в том, что это справедливо только для земной системы отсчета. Сядем снова в машину и положим мяч на плоскую поверхность. Если машина повернет влево, наш мяч покатится вправо, так же как мы наклоняемся к правой дверце. Это видно на рис. 2.3: мяч (кружок) в определенный момент оказывается в правой части машины. Также если машина затормозит, мяч покатится вперед, как мы наклоняемся к лобовому стеклу. Это также наглядно показано на рис. 2.4, где мяч на секунду оказывается перед машиной.
Таким образом, в системе отсчета машины неподвижный предмет не остается неподвижным: поскольку он испытывает ускорение, его движение перестает быть прямолинейным и равномерным.
То есть законы движения зависят от системы отсчета, а прямолинейная равномерная траектория изолированного объекта применима лишь в некоторых особых системах отсчета. Эти особые системы отсчета очень важны, ибо мы видим, что наша старая добрая земная система отсчета на первый взгляд относится к этой категории. Такие системы называются «инерциальными системами отсчета».
Таким образом, движение изолированного объекта в инерциальной системе отсчета является прямолинейным и равномерным по определению этой системы отсчета.
Какие системы отсчета являются инерциальными?
Загвоздка в том, что земная система отсчета не такая уж инерциальная. Покатим наш мяч по плоской поверхности в несколько километров длиной, предположив, что трения не существует: если долго смотреть на его траекторию, мы увидим, что мяч немного отклоняется вправо и описывает широкую дугу. Причина этого в том, что Земля вращается вокруг своей оси: именно это явление заставляло наш мяч катиться вправо в машине, которая поворачивала налево.
Мы постараемся более детально вникнуть в точное движение мяча по отношению к Земле в следующей главе: а сейчас достаточно констатировать, что система отсчета не является инерциальной при длительном наблюдении за движением из-за вращения Земли.
Но если геоцентрическая система не вращается вокруг своей оси, является ли она инерциальной, в отличие от земной? Увы, Земля вращается вокруг Солнца, а вместе с ней и геоцентрическая система отсчета: это сопровождается теми же последствиями для движения тел. То же самое происходит с гелиоцентрической системой, которая «вращается» вокруг центра Галактики.
На самом деле ни одна из этих трех систем отсчета не является инерциальной, но более или менее к ней приближена. Земная система отсчета может в целом рассматриваться как инерциальная, кроме тех случаев, когда нас интересуют крупномасштабные пространственные явления (например, движение масс воздуха и океанов) или когда мы хотим очень подробно изучить некоторые движения. Геоцентрическая и гелиоцентрическая системы отсчета являются вполне инерциальными для большинства изучаемых движений.

АБСОЛЮТНАЯ СИСТЕМА ОТСЧЕТА?
И последнее: поскольку инерциальная система отсчета так интересна, можем ли мы считать ее «абсолютной», считать ее системой отсчета Вселенной, в которой все предметы находятся в движении?
На самом деле можно продемонстрировать, что инерциальная система отсчета не единственная и существует множество других.
Возьмите лист бумаги и ручку, которая будет представлять изолированный объект. Проведите вертикальную черту сверху вниз, двигая ручку с постоянной скоростью: у вас получилась красивая равномерная прямолинейная траектория, а ваш лист представляет собой инерциальную систему отсчета.
Теперь проделайте то же самое, медленно передвигая лист влево с одинаковой скоростью: на этот раз черта будет диагональной, но по-прежнему прямой и нарисованной с постоянной скоростью. То есть лист, медленно перемещенный влево, также представляет собой инерциальную систему отсчета.
Таким образом, оба ваших листа представляют собой инерциальные системы отсчета, находящиеся в движении по отношению друг к другу.
В действительности любая система отсчета, которая равномерно перемещается по прямолинейной траектории по отношению к инерциальной системе отсчета, также является инерциальной: таким образом, существует бесконечное множество инерциальных систем отсчета, находящихся в движении по отношению друг к другу.
Идея «абсолютной системы отсчета» не имеет решительно никакого смысла.
Существует ли совершенная инерциальная система? Да, существует, но она представляет мало интереса… Как правило, мы стремимся изучить движение тела по отношению к чему-то конкретному (к земной поверхности, к планете Земля, к Солнцу), а вместе с этим возникает и определенная система отсчета.
Может возникнуть вопрос, зачем так подробно останавливаться на понятии инерциальной системы. В действительности, как мы увидим в дальнейшем, в этой системе отсчета законы механики наиболее просты: поэтому всегда приятно, когда можешь считать свою систему отсчета инерциальной…
2. Сила и инерция
В повседневной речи ускорение означает увеличение скорости. С точки зрения физика это не всегда верно по двум главным причинам:
• Ускорение – это алгебраическая величина, то есть оно может быть положительным и отрицательным, в зависимости от того, увеличивается скорость или уменьшается. Физик никогда не скажет «замедление», для него речь идет об «отрицательном ускорении»… То есть машина, которая тормозит, испытывает ускорение!
• Еще важнее то, что скорость представляет собой вектор, то есть стрелку, направление которой указывает направление траектории (например, на север), а длина указывает величину скорости (например, 50 км/ч обозначается стрелкой длиной 50 мм).
Однако физик считает, что ускорение наступает тогда, когда меняется вектор скорости: то есть когда меняется скорость, но и когда меняется направление траектории.
Например, машина, которая поворачивает налево, испытывает ускорение, даже если ее скорость (50 км/ч) не меняется: зато меняется направление вектора скорости.
Итак, необходимо запомнить два очень разных влияния ускорения:
• Если ускорение параллельно траектории, оно меняет скорость, но не направление машины. В этом случае ускорение называется тангенциальным (➙ рис. 1.5).
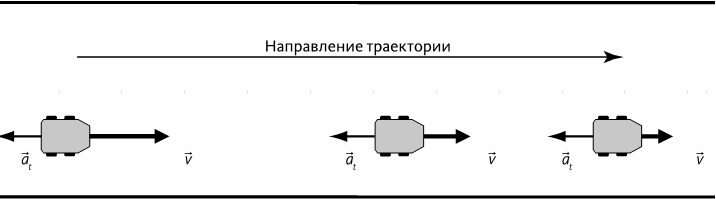
Рис. 1.5 – Векторы скорости и ускорения во время торможения.
Машина тормозит: с одной стороны стрелка вектора скорости v→; становится все короче, с другой стороны тангенциальное ускорение a→;t направлено назад.
• Если ускорение перпендикулярно траектории движения, оно меняет направление машины, но не меняет ее скорость: в этом случае ускорение называют центростремительным (➙ рис. 1.6).
Конечно, может быть и так, что оба ускорения действуют одновременно, меняя скорость и направление.

Рис. 1.6 – Векторы скорости и ускорения во время поворота.
Машина поворачивает влево: с одной стороны вектор скорости v→; все больше склоняется влево, с другой стороны вектор нормального ускорения a→;n направлен влево.

ВЕЛИЧИНА УСКОРЕНИЯ
Тангенциальное ускорение показывает изменение скорости за секунду: так, если скорость машины меняется за секунду с 30 м/с на 20 м/с, ее ускорение равно – 10 м/с² (потеря скорости составляет 10 м/с каждую секунду).
А как обстоит с центростремительным ускорением? Как можно его измерить, если скорость машины не меняется? В этом случае необходимо значение, указывающее на «размер изменения направления».
Предположим, что за одну секунду вектор скорости меняется с v→;1 на v→;2, меняя только направление (см. схему справа). Мы видим, что стрелка вектора описала дугу, длина которой и составляет величину ускорения (математика очень точно нам это демонстрирует). Чем длиннее стрелки и больше угол между векторами, тем длиннее будет дуга.
Таким образом, центростремительное ускорение равно скорости, помноженной на изменение угла за единицу времени.
Действие окружающей среды
Снова возьмем наш объект, движущийся в инерциальной системе отсчета. Предположим, что это космический корабль, затерянный в безвоздушном межзвездном пространстве: то есть он является изолированным объектом, а его траектория равномерная и прямолинейная. А теперь представим, что он приближается к какой-то планете: его траектория искажается, несмотря на то что он не взаимодействует с планетой.
Если говорить в гораздо более широком смысле, мы наблюдаем, что малейшее материальное окружение искажает траекторию любого объекта. Это влияние может быть самым разным, например, стена жестко изменит нашу равномерную прямолинейную траекторию, если мы в нее врежемся. Если мы захотим пролететь по прямой линии с крыши одного дома на крышу другого, Земля может помешать нам проделать путь по прямолинейной траектории, заставив нас упасть. Или если мы едем на велосипеде, а ветер встречный, воздух может сильно тормозить наше движение, заставляя нас терять равномерную скорость, и т. д.
Таким образом, во всех случаях наша прямолинейная равномерная траектория искажается под действием окружающей среды:
• она или перестает быть равномерной, то есть на нас действует тангенциальное ускорение;
• или же она перестает быть прямолинейной, то есть мы испытываем влияние нормального ускорения.
В обоих случаях возникает ускорение, которого не существовало бы, если бы мы были изолированным объектом.
Запомним: в инерциальной системе отсчета присутствие материальной окружающей среды приводит к ускорению рассматриваемого объекта.
Два важнейших параметра: сила и инерция
Чем больше ускорение, тем больше мы уклоняемся от первоначальной равномерной и прямолинейной траектории, то есть воздействие на нас окружающей среды будет «сильнее». Следовательно, сила, с которой на нас воздействует окружающая среда, измеряется относительно нашего ускорения.
Таким образом, действующую на нас силу мы можем считать равной нашему ускорению. Однако интуитивно понятно, что это не так, и это можно продемонстрировать на простом примере.
Предположим, что вас попросили толкнуть детскую коляску так, чтобы она переехала улицу: вы сможете это сделать без особых усилий. Чуть погодя вас просят помочь подтолкнуть заглохшую машину: вам будет очень трудно сдвинуть ее – то есть придать ей ускорение – в одиночку. Таким образом, мы видим, что одна и та же сила, направленная на два разных объекта, приводит к двум различным ускорениям.
Каждый объект, испытывающий ускорение, обладает присущим ему свойством, а именно инертностью, которая является способностью объекта сопротивляться всякому ускорению в заданном пространстве.
Напрашивается вывод: чем более крупным и тяжелым выглядит объект (например, машина), тем сложнее, кажется, придать ему ускорение, а следовательно, тем больше его инертность. Вот почему инертность еще называют инертной массой («инертная» от слова «инерция») и выражают ее в килограммах.
Подведем итог: в инерциальной системе отсчета ускорение объекта тем больше, чем меньше его инертная масса и чем больше сила воздействия окружающей среды. Таким образом, ускорение является следующим соотношением силы (связанной с окружающей средой) и инертной массы (присущей объекту): a→; = F→;/m (где a→; – это ускорение, F→; – сила, а m – инертная масса).
Записывают также и по-другому: (F→; = ma→;) в инерциальной системе отсчета.

УТОЧНЕНИЯ ПО ОБЛАСТИ ПРИМЕНЕНИЯ
До сих пор мы говорили об объектах, чья скорость была определена. Но как обстоит дело, к примеру, с вращающимся диском? Если нас интересует его центр, то в земной системе отсчета его скорость является нулевой. Если же нас интересует его поверхность, то она вращается с большой скоростью. По правде говоря, каждая точка диска имеет разную скорость и ускорение. Какая же сила приложена к этому объекту, если его ускорение в разных точках не является одинаковым?
Подобные вращающиеся объекты мы рассмотрим в главе 7. А пока ограничимся объектами, чья скорость и ускорение во всех точках одинаковы, то есть такими, которые находятся в поступательном движении, а не вращаются вокруг своей оси.
Та же проблема возникает, если объект деформируется (в каждой точке возникает разная скорость), и тем более если он распадается на две части. Например, так происходит с ракетой, теряющей сгоревшие газы по мере своего ускорения: газы, бывшие неотъемлемой частью ракеты, внезапно оказываются предоставленными самим себе и обретают собственную скорость.
Но подобные случаи, в общем, достаточно редки, и в дальнейшем повествовании мы с легкостью будем их избегать.
Это простое уравнение описывает дифференциальный закон механического движения, или второй закон Ньютона (см. врезку ниже). С тех пор в честь этого выдающегося ученого сила выражается в ньютонах: эту единицу измерения мы крайне редко используем в повседневной жизни, но для каждого физика она является основополагающей!
Заметим, что до сих пор мы не сказали ничего революционного: мы ограничились определением инерциальной системы отсчета и силы так, чтобы они наилучшим образом соответствовали интуитивному смыслу, имея при этом четко определенные рамки. Что касается инертной массы, мы чувствуем, что она тем или иным образом связана с весом объекта, однако пока что ограничимся тем, что речь идет о некоем загадочном свойстве, присущем каждому объекту.

СИЛА И ЕЕ СОСТАВЛЯЮЩИЕ
Сила, описанная во втором законе Ньютона, складывается из общего влияния окружающей среды. Но мы всегда ради интереса можем мысленно поделить эту силу на несколько составляющих.
Например, возьмем машину, которая движется по улице с ускорением. Поскольку она движется с ускорением, это значит, что на нее действует сила окружающей среды, направленная вперед. Мы можем разделить эту силу на четыре составляющих (см. схему ниже):
• сила тяги, которую создают мотор и колеса, направленная вперед;
• сила трения, которое создает воздух, направленная назад;
• вес машины, направленный вниз;
• сопротивление почвы, не дающее машине пройти сквозь нее, направленное вверх.
Эти четыре составляющих и создают силу F→;, которая позволяет машине двигаться с определенным ускорением (F→; = ma→;), где F→; – равнодействующая всех сил. В последующих главах мы более подробно остановимся на происхождении и выражении этих разных сил.

Настало время четко понять, как окружающая среда оказывает влияние на объекты, что приведет нас к описанию двух основополагающих сил Вселенной: силы притяжения и электромагнитной силы. Нам кажется, что повседневной жизнью управляет множество других сил (когда мы ударяемся о стену, на нас действует некая самостоятельная сила, не правда ли?): мы увидим, что все они являются следствием этих двух фундаментальных сил.

ПОНЯТИЕ «ЗАКОНА» В ФИЗИКЕ
При описании дифференциального закона механического движения мы впервые столкнулись с понятием «закон»: в дальнейшем мы познакомимся и с другими. Необходимо усвоить, что «физические законы» ни в коем случае не являются эмпирическими константами, универсальность которых можно было бы допустить. Чаще всего речь будет идти об отношениях, вводящих новую величину, которые верны по определению, по своей природе определенные законы не могут быть ложными.
Например, дифференциальный закон механического движения позволил ввести такое понятие, как «сила» и «инертная масса». Также мы увидим, что «первый закон термодинамики» всего лишь описывает понятие «полной энергии», придуманное физиками.
Таким образом, нам станет ясно, что физика вовсе не является объемным каталогом экспериментальных законов: вся классическая физика действительно сводится к выражению двух фундаментальных сил.

СЛЕДУЕТ ЗАПОМНИТЬ
• Понятие движения имеет смысл только по отношению к определенной характеристике, которую физики называют системой отсчета.
• В большинстве случаев нас интересует движение по отношению к поверхности земли: земная система отсчета.
• В инерциальной системе отсчета движение объекта по определению является равномерным и прямолинейным. Земную систему отсчета можно считать инерциальной, учитывая большинство видов движения в повседневной жизни.
• С точки зрения физика ускорение приводит к изменению вектора скорости, а значит, к изменению величины скорости и/или ее направления.
• Инертная масса оказывает сопротивление ускорению объекта в инерциальной системе отсчета в заданном пространстве.
• В инерциальной системе отсчета сила, с которой окружающая среда воздействует на твердый объект в поступательном движении, определяется как произведение ускорения объекта и его инертной массы.
2. Сила притяжения
Из двух фундаментальных сил классической физики сила притяжения, удерживающая нас на поверхности Земли, выражена наиболее явно. Мы рассмотрим более подробно ее происхождение и последствия, что значительно расширит наше понятие о массе, с которым мы познакомились в предыдущей главе. Мы увидим, что существует три концептуально различных и тем не менее одинаковых массы, что является одной из великих загадок физики.
Рассмотрим феномен приливов и отливов, причиной которых является сила притяжения: мы увидим, что они касаются не только земных океанов, но также управляют множеством других явлений Солнечной системы.
1. Выражение силы притяжения
Притяжение между двумя телами
Сила притяжения управляет нашей повседневной жизнью: необязательно быть внимательным наблюдателем, чтобы понять, что земная поверхность неизбежно притягивает к себе все предметы. И что эта сила действует на расстоянии: спрыгните с летящего самолета, чтобы убедиться в этом! Но если мы выкопаем яму, наше падение вниз продолжится и там, то есть нас притягивает центр Земли.
А теперь вопрос: если все тела испытывают земное притяжение, то же самое должна испытывать и Луна: почему же она не падает?
Переместимся немного повыше и представим себя в геоцентрической системе отсчета: мы находимся в космосе и видим, как Земля медленно вращается у нас под ногами. Речь идет об инерциальной системе отсчета. Это значит, что при отсутствии воздействующей силы Луна должна иметь равномерную прямолинейную траекторию, а значит, должна была бы уже давно отдалиться от Земли. Однако Луна вращается вокруг Земли, то есть испытывает «нормальное ускорение», заставляющее ее описывать дугу (➙ рис. 2.1). Но где ускорение, там и сила, направленная в сторону ускорения, то есть… прямо к Земле! А вот и результат!

Рис. 2.1 – Сила Земли, воздействующая на Луну и на яблоко
Таким образом, Земля притягивает все, абсолютно все: это она заставляет яблоко падать с дерева, и она же удерживает Луну на ее орбите. К такому гениальному выводу пришел Ньютон, который первым сформулировал понятие гравитации.
Мы могли бы представить некое загадочное «притягивающее тело» в центре Земли, так же как в центре любой планеты и любой звезды. Но мы также можем предположить, что притяжение осуществляет обычная материя, из которой состоит Земля.
Напрашивается простой вывод: если обычная материя способна притягивать предметы на расстоянии, мы, человеческие существа, состоящие из материи, также должны притягивать к себе другие тела! Первый же прохожий на улице должен испытывать наше непреодолимое притяжение…
Так ли это? Ответ – да! Но это притяжение ничтожно и невидимо для нас. Зато его можно определить с помощью современных измерительных приборов: подвесьте к потолку два очень тяжелых шара на веревках так, чтобы они не касались друг друга (такой подвес называют маятником). Вы «увидите» (с помощью измерительного прибора), что оба маятника наклонены друг к другу, а вовсе не висят вертикально (впервые подобное измерение было проделано в 1798 г.).
Способность притягивать и способность притягиваться
Чем больше измерений мы сделаем, тем вернее убедимся в том, что чем большим весом и плотностью обладает тело, тем сильнее его способность притягивать окружающие предметы: это называют активной гравитационной массой, свойственной каждому объекту, которая отражает его способность притягивать другие объекты и выражается в килограммах.
Не следует путать ее с инертной массой, которая является инерцией объекта, то есть его сопротивляемостью ускорению. В то время как активная гравитационная масса представляет собой его способность притягивать другие тела. То есть на первый взгляд между ними нет никакой связи: единственный вывод – обе массы тем больше, чем больше вес и плотность объекта.
Это объясняет, почему Земля, которая представляет собой гигантское тело, с такой силой притягивает предметы, в то время как мы сами, хилые человечки, слишком малы, чтобы осуществлять видимое притяжение.
Таким образом, сила притяжения, действующая на объект, пропорциональна активной гравитационной массе притягивающего тела. Продолжим наше исследование новым опытом.
Поднимем два предмета: левой рукой теннисный шарик, а правой чугунное ядро каторжника. Ядро покажется нам гораздо тяжелее шарика. Поскольку ядро поднять сложнее, значит, сила притяжения, которая действует на него, больше, чем та, что действует на теннисный шарик.
Таким образом, сила притяжения также зависит еще от одного параметра, свойственного объекту, на который она воздействует: он называется пассивной гравитационной массой, выраженной в килограммах, которая точно соответствует интуитивному смыслу массы. В нашем случае чугунное ядро имеет гораздо большую пассивную гравитационную массу, чем теннисный шарик, потому что оно тяжелее: сила притяжения, действующая на него, гораздо больше, чем та, что действует на теннисный шарик.

ПРОГУЛКА ПО ЛУНЕ
На Луне астронавт чувствует себя очень легким: и действительно, активная гравитационная масса Луны гораздо меньше, чем у Земли, и сила ее притяжения слабее. Астронавт, прогуливающийся по Луне, может прыгать как кузнечик, все выше и выше, все дальше и дальше… пока со всего маху не натолкнется на первое же препятствие, которое перед ним возникнет.
На самом деле то, что астронавт стал легче, не означает, что его инертная масса стала меньше: масса тела является параметром, присущим каждому телу, и везде остается одинаковой. Инертность астронавта остается той же, что и на Земле, но, поскольку он чувствует себя легче, он забывает об этом. Прыгать он сможет выше, но от толчка инерция повлечет его с той же силой, что и на Земле. Соединение малого веса и большой инертности будет новым опытом для него, и ему придется двигаться с осторожностью.
Как же много получается разных масс! Пора подвести некоторый итог:
• инертная масса представляет собой сопротивляемость объекта ускорению;
• активная гравитационная масса представляет собой способность тела гравитационно притягивать к себе другие объекты;
• пассивная гравитационная масса представляет собой способность тела быть гравитационно притянутым другим телом.
Именно эту последнюю массу мы в повседневном обиходе именуем «весом»: когда мы говорим, что человек весит 60 кг, это означает, что его пассивная гравитационная масса равна 60 кг. А человек с весом в 100 кг испытывает двойное гравитационное притяжение по сравнению с тем, кто весит 50 кг.
Чтобы следовать дальше и более подробно рассмотреть силу притяжения, ее необходимо изолировать от других сил: лучше всего переместиться на Луну, где трение воздуха не создаст помех, поскольку там нет атмосферы.
Там мы сможем провести два заключительных опыта, результаты которых ошеломляют…
Синхронное падение двух тел
Гордо помашем чугунным ядром в одной руке и теннисным шариком в другой на одинаковой высоте. Одновременно бросим на землю: против всякого ожидания и ядро и шарик достигнут пола в одно время. Это значит, что оба предмета получили одинаковое ускорение. (Опыт с перышком и молотком был проделан астронавтами корабля «Аполлон» в 1969 г.)
На предметы действуют две силы, противоположные друг другу:
• более высокая инертная масса ядра стремится замедлить его падение (ускорение затруднено);
• более высокая пассивная гравитационная масса ядра заставляет его испытывать более сильное притяжение Луны, что «толкает его вперед».
Поскольку ускорение обоих предметов одинаково, из этого следует, что действующие на них вышеупомянутые нагрузки уравновешивают друг друга: следовательно, инертная масса равна пассивной гравитационной массе. Результат, который никак невозможно было предвидеть!
Взаимное притяжение двух тел
Теперь проделаем второй опыт, похожий на первый и с таким же поразительным результатом. Подцепим наше ядро и теннисный шарик к двум горизонтальным пружинам высокой растяжимости, расположенным друг напротив друга (➙ рис. 2.2). Оба предмета притягиваются друг к другу благодаря силе притяжения, действующей между двумя телами, хотя этого и не видно невооруженным глазом. Чем сильнее растянута пружина, тем сильнее ее «тянет» предмет и, следовательно, тем больше сила притяжения предмета напротив.

УСКОРЕНИЕ ОДИНАКОВОЕ, СИЛЫ РАЗНЫЕ
Мы увидели, что чугунное ядро и теннисный шарик, сброшенные на Луне с одинаковой высоты, падали с одинаковой скоростью: означает ли это, что сила удара по поверхности Луны у обоих предметов одинакова? Ответ «нет», потому что, даже если их ускорение и одинаково, инерция (= инертная масса) у них разная: когда ядро брошено, его уже очень трудно остановить, разве что приложить колоссальное усилие. Однако когда ядро касается поверхности Луны, его скорость внезапно меняется с 8 км/ч на 0 км/ч, что потребует от почвы огромной силы: возможно, ядро оставит небольшую вмятину на месте падения, в то время как теннисный шарик подскочит, не нанеся ущерба.
Чья пружина растянута больше, ядра или шарика? Ответ на этот вопрос однозначен: обе пружины растянулись одинаково, а это значит, что ядро и шарик с одинаковой силой притягивают друг друга.

Рис. 2.2. – Гравитационное притяжение между ядром и шариком
Здесь также действуют силы, противоположные друг другу:
• активная гравитационная масса ядра больше массы шарика, то есть ядро сильнее притягивает шарик (который стремится сильнее растянуть пружину);
• пассивная гравитационная масса ядра больше массы шарика, поэтому ядро сильнее притягивается шариком (и старается сильнее растянуть пружину).
Поскольку обе пружины растянуты на одинаковую длину, значит, обе нагрузки компенсируют друг друга: то есть активная гравитационная масса равна пассивной гравитационной массе.
Загадочное равенство
Таким образом, оба наших эксперимента выявили совершенное равенство:
Вот почему все три величины называют массой! Впрочем, в дальнейшем мы будем говорить просто о «массе» объекта, не уточняя, о какой именно.
Если результаты этих двух опытов кажутся вам «странными» и «волшебными», значит, вы все поняли!
Тождество «гравитационная масса = инертной массе» (а именно: «Два тела, брошенные одновременно, падают с одинаковой скоростью») всегда чрезвычайно интриговало физиков. Именно это и подтолкнуло Эйнштейна к созданию общей теории относительности, которая создает новую теорию гравитации: в дальнейшем мы обязательно к ней вернемся.
Равенство двух гравитационных масс («Силы, действие которых испытывают на себе два взаимодействующих предмета, равны») остается таким же загадочным с тех пор, как его открыл Ньютон. В дальнейшем оно позволит нам говорить просто о взаимном притяжении двух тел, не уточняя, кто кого притягивает, поскольку тела притягивают друг друга с одинаковой силой.

НЕВЕРНОЕ ОПРЕДЕЛЕНИЕ?
Равенство двух гравитационных масс означает, что сила, с которой теннисный шарик действует на ядро, равна силе, с которой ядро действует на теннисный шарик (что подтверждается предыдущим опытом). Однако это справедливо для любого тела: например, сила, с которой вы действуете на Землю, идентична той, с которой Земля воздействует на вас!
Вы не чувствуете себя настолько сильным? Такой результат поначалу кажется абсурдным, но все-таки он верен. Но важно понять, что ускорение будет очень разным: Земля обладает огромной инертностью (= огромной массой) и не сдвинется ни на миллиметр на ваших глазах, несмотря на огромную силу, с которой вы на нее воздействуете, в то время как ваша смехотворная инертность делает вас для Земли просто «игрушкой».
Возможно, все эти на первый взгляд странные заключения происходят от того, что определение, которое мы дали силе, неверно и не соответствует здравому смыслу. Мы представили силу в виде отношения F→; = ma→; в инерциальной системе отсчета. Не лучше ли записать, что F→; = a→;?
И действительно, если ускорение объектов одинаково, учитывать инертную массу нет никакого смысла: определенное пространство (= «определенная F→;») вызывает определенное ускорение (= «определенная a→;») независимо от рассматриваемого объекта (= m не играет роли). В этом случае мы находим силу, с которой Земля действует на нас, большой, а силу, с которой мы действуем на Землю, – незначительной: а это все же гораздо более интуитивное ощущение.
На самом деле, как всякий уважающий себя физик, в дальнейшем мы будем придерживаться нашего первого определения F→; = ma→;. Почему? Потому что электромагнитная сила придает объекту ускорение, которое зависит от его параметров, что вновь придает смысл упомянутой «m» (инертности объекта). Между тем вопреки всякому ожиданию именно электромагнитная сила в большей степени управляет нашей повседневной жизнью, хотя на первый взгляд она кажется совершенно скрытой от глаз. Именно это мы увидим в следующей главе.
Мы еще не закончили с гравитацией, разберем-ка ее поподробнее.
Вполне естественно, что сила притяжения уменьшается, если расстояние между двумя объектами увеличивается. В противном случае Солнце притягивало бы нас гораздо сильнее Земли, и мы давно бы на нем изжарились.

ЗАГАДОЧНОЕ ДЕЙСТВИЕ НА РАССТОЯНИИ
Может показаться удивительным, что два тела, разделенные пустотой, могут взаимодействовать друг с другом. Например, как Луна может создавать приливы и отливы на Земле, если ни один «вестник» не сообщает океанам о присутствии Луны, находящейся в 380 000 км над нами.
Тем не менее современная физика полагает, что всякое массивное тело испускает во все стороны такие частицы «вестники», называемые гравитонами. Именно они, достигнув объекта, сообщают ему о присутствии притягивающего тела и создают таким образом силу притяжения.
Эта гипотеза позволяет проще понять, почему гравитация уменьшается пропорционально квадрату расстояния.
Возьмем массивное ядро, которое испускает, к примеру, сто гравитонов в секунду во всех направлениях. Когда гравитоны преодолеют расстояние в 1 м, они будут распределены по поверхности сферы с радиусом 1 м, центром которой является ядро, а площадь составит 12,5 м² (площадь сферы с радиусом r равна 4πr²).
Когда гравитоны преодолеют 10 м, они будут распределены по сфере с радиусом 10 м, то есть на площади 1250 м². Таким образом, на одной единице площади будет в 100 раз меньше гравитонов, если расстояние до ядра увеличится в 10 раз (см. схему ниже).
Мы видим уменьшение, пропорциональное квадрату расстояния. А если число гравитонов разделить на 100, сила притяжения будет в 100 раз слабее, то есть сила притяжения подчиняется тому же закону уменьшения.
Гравитоны пока не были обнаружены из-за отсутствия достаточно точных приборов, но физики почти уверены, что они существуют. Им даже известна их скорость, которая равняется скорости света. Описание электромагнитной силы позволит нам понять, почему физики позволяют себе такую уверенность.

Если точнее, измерения показывают, что сила притяжения уменьшается пропорционально квадрату расстояния: если расстояние между объектами увеличилось в десять раз, сила притяжения уменьшится в сто раз.
Итак, теперь нам известно, что такое гравитация! Подведем итоги:
• Сила притяжения пропорциональна активной гравитационной массе притягивающего тела.
• Сила притяжения пропорциональна пассивной гравитационной массе притягиваемого тела.
• Сила притяжения обратно пропорциональна квадрату расстояния.
Осталось уточнить размер силы для заданных массы и расстояния, чтобы представлять себе порядок величин. И результат довольно поразительный: сила, действующая между двумя объектами массой 1 кг, находящимися на расстоянии 1 м, в 10 миллиардов раз меньше, чем сила, необходимая, чтобы открыть дверь с хорошо смазанными петлями! Понятно, что притянуть прохожего на улице нам не удастся…
Частное значение этой силы, действующей между двумя объектами массой 1 кг на расстоянии 1 м, называется гравитационной постоянной и обозначается G: именно она является коэффициентом гравитационного взаимодействия, с помощью которого можно измерить силу притяжения, действующую на любое тело независимо от его массы и расстояния до него. G является одной из фундаментальных физических констант, чье значение может быть установлено без дополнительных пояснений.

ВЫРАЖЕНИЕ СИЛЫ ГРАВИТАЦИИ
Сила притяжения, осуществляемая телом с массой М на объект с массой m, находящийся на расстоянии d, выражается следующим образом:

Чтобы найти силу, с которой объект с массой m действует на тело с массой М, достаточно поменять местами М и m: мы увидим, что выражение силы не меняется. Таким образом, два взаимодействующих тела подвергаются действию одинаковой силы благодаря тому, что их гравитационные массы равны (М и m взаимозаменяемы).
Поскольку сила выражена вектором, необходимо указать ее направление: она направлена в сторону ускорения в инерциальной системе отсчета, то есть в сторону притягивающего тела.
Другое название силы притяжения
В предыдущих параграфах мы самым подробным образом рассмотрели понятие различных масс, но лишь вскользь упомянули понятие «вес».
Определение веса не так уж сложно: весом объекта называется сила, с которой он действует на поверхность земли, находясь в неподвижном состоянии. Однако эта сила практически полностью складывается из земного притяжения. Таким образом, можно приблизительно констатировать, что вес – это просто другое название силы притяжения.
В основном мы употребляем слово «вес», когда говорим об объектах, находящихся в непосредственной близости к поверхности планеты (в повседневной жизни), но употребляем понятие «сила притяжения», когда речь идет о космических объектах (спутниках, планетах, звездах).
Таким образом, когда мы говорим, что «весим» больше, чем кто-либо, это означает, что мы испытываем большую силу притяжения.
То есть понятие «вес» отличается от понятия «масса», как мы уже говорили, – если вы попадете на Луну, ваша масса останется прежней (этот параметр свойственен объекту); но вы будете «весить» меньше, потому что сила притяжения, действующая на вас, будет меньше.
Вернемся на Землю, где все нам привычнее. От чего же зависит вес объекта?
• разумеется, от его массы;
• от массы притягивающего тела, в данном случае Земли (она одинакова для любого объекта, расположенного на Земле);
• от гравитационной постоянной G, одинаковой для всех, как и указывает ее название;
• от расстояния между двумя взаимодействующими телами, в данном случае между Землей и объектом.
Каково это расстояние? 0 км – раз объект находится на поверхности Земли? Поскольку Земля огромна, ее масса понемногу распределена повсюду под нами, то есть определять расстояние до Земли не имеет смысла. Однако можно продемонстрировать (спасибо математике!), что все происходит так, будто масса Земли сосредоточена в ее центре. Но от центра Земли нас отделяет ее радиус, равный 6380 км, а это означает, что, если бы вся Земля целиком находилась от нас на расстоянии 6380 км, она действовала бы на нас с той же силой.
Таким образом, радиус Земли и есть то самое расстояние от Земли до объекта. И оно одинаково абсолютно для всех: даже если вы подниметесь на вершину Эвереста (8,8 км), вы почти не удалитесь от центра Земли (6389 км вместо 6380 км).

СТРАШНАЯ СТРЕЛКА ВЕСОВ
Встаньте на весы: что они показывают? Значение в килограммах, которое соответствует массе. Однако не стоит торопиться…
На самом деле весы испытывают на себе силу, с которой вы на них воздействуете (например, с помощью маленьких пружин, которые сжимаются слабее или сильнее, в зависимости от комплекции и роста человека). Однако сила, с которой вы действуете на весы, возникает из-за земного притяжения, что и является вашим весом. Таким образом, весы измеряют вес, а не массу, но почему же в таком случае они показывают результат в килограммах, а не в ньютонах?
Причина в том, что вес и масса связаны отношением P = mg. Но на Земле g = 10mc ², то есть между весом и массой добавляется коэффициент 10. Поэтому вместо того, чтобы показать 600 ньютонов (величину веса), весы покажут 60 кг (вашу массу). Коэффициент 10 в каком-то смысле заложен внутри весов.
Это значит, что ваши весы могут служить только на Земле, поскольку коэффициент g = 10 m/c² существует только на Земле! Отвезите весы на Луну, где сила тяжести в 6 раз слабее, и весы покажут 10 кг, потому что измеренный вес будет равняться 100 ньютонам.
Но не радуйтесь раньше времени, потому что этот результат ложный! Ваша масса по-прежнему равна 60 кг, просто ваш вес был поделен на 6.
В конечном итоге все эти параметры постоянны, за исключением массы объекта, которая зависит… от самого объекта! Также мы констатируем, что вес равняется произведению массы объекта m и константы g, единой для всех. Эта константа называется ускорением свободного падения. Она присуща любой планете и зависит, как мы увидели, от ее массы и ее радиуса.
Если обозначить вес буквой P, мы получим формулу P→; = mg→;.
Стрелка представляет собой вектор, чье направление следует уточнить: сила направлена к центру Земли, а значит, ускорение свободного падения тоже.
Ускорение свободного падения
Выражение веса P→; = mg→; очень похоже на выражение силы F→; = ma→;. Оно является верным для инерциальной системы отсчета, которой в первом приближении является земная система отсчета. Однако единственной силой, действующей на объект в свободном падении, является вес, то есть это можно записать как F→; = P→; или, используя двойное соотношение, ma→; = mg→;. Получается, что a→; = g→;. Таким образом, поле тяготения соответствует ускорению свободного падения объекта, каким бы он ни был. Поэтому величина g также называется ускорением свободного падения. Мы обнаруживаем, что все объекты, брошенные одновременно, падают с одинаковой скоростью, если на них действует только их вес.
Между тем g является константой, которую легко вычислить: на Земле она составляет примерно 10 м/с². Это означает, что в свободном падении на Земле скорость любого объекта каждую секунду возрастает на 10 м/с, то есть на 36 км/ч. То есть по прошествии 10 секунд объект движется уже со скоростью 360 км/ч!
Разумеется, на практике на объект действует и другая сила, которая его тормозит, – сопротивление воздуха. А значит, реальная скорость объекта будет гораздо ниже и даже стабилизируется, если объект сброшен с большой высоты: именно в этом состоит смысл парашюта, к которому мы вернемся в дальнейшем.

НЕВЕСОМОСТЬ
Вы едете в лифте, когда внезапно трос обрывается, и вы оказываетесь в свободном падении. Ускорение свободного падения одинаково для всех тел, поэтому и вы и лифт падаете с одинаковой скоростью. Это значит, что по отношению к лифту у вас нет никакого ускорения: не двигаясь, вы можете находиться внутри лифта в подвешенном состоянии. Иными словами, вы в невесомости.
Теперь перенесемся на Международную космическую станцию на орбите на высоте 350 км. Вы и космическая станция испытываете ускорение свободного падения, и именно оно удерживает вас на орбите, препятствуя вашему движению по прямой. Вы и станция подвержены одинаковому ускорению, то есть по отношению к станции у вас нет никакого ускорения. Так же как и в лифте, вы находитесь в состоянии невесомости.
Итак, если космонавты в космической станции находятся в состоянии невесомости, это не означает, что на них не действует гравитация (вес в космосе всего на 4 % меньше, чем на Земле): просто они испытывают такое же ускорение, что и станция.
В конечном итоге, если для того, чтобы оказаться в невесомости, нужно полететь в космос, это потому, что необходимо выйти из атмосферы, трение которой заставило бы упасть станцию на Землю. Пример с лифтом показывает, что можно испытать невесомость и на Земле, но этот опыт будет гораздо более кратким.
На практике существует специальный аэробус, предназначенный для тренировки космонавтов в атмосфере, – какое-то время самолет находится в свободном падении, прежде чем выровняться, не достигнув земли.
2. Приливы и отливы
Рассмотрим гравитационное воздействие Луны на Землю (➙ рис. 2.3). Сила воздействия Луны на объект будет различаться в зависимости от того, в какой точке Земли он находится. Если Луна на небе в зените, значит, объект находится от нее на кратчайшем расстоянии и испытывает наиболее сильное воздействие (точка А). Антиподы этой точки, находящиеся на противоположной стороне Земли, значительно удалены от Луны: их разделяет еще и диаметр Земли. То есть сила воздействия Луны на объект в этой точке значительно слабее (точка В). А если бы объект находился в центре Земли, сила воздействия Луны была бы средней (точка О).
Эта разница уровня силы обнаруживается в формуле ускорения (F→; = ma→;). В то же время любые тела, расположенные на определенном расстоянии от Луны, испытывают по отношению к Луне одинаковое ускорение вне зависимости от их массы.
Мы убедились, что Земля ведет себя так, словно вся ее масса сосредоточена в центральной точке О. Таким образом, Земля целиком испытывает ускорение средней силы: слабее, чем объект на ее поверхности в точке А (со стороны Луны), но более сильное, чем объект в точке В (антипод).

Рис. 2.3 – Сила воздействия Луны в различных точках Земли
В точке А Луна находится в зените, здесь ее воздействие максимально. Точка В – антипод, в ней воздействие Луны минимально. Точка О находится в центре Земли, здесь воздействие средней величины.
Мы говорим об ускорении по отношению к Луне; но рассмотрим теперь, каково оно по отношению к Земле. Объект в точке испытывает большее ускорение, чем Земля, то есть он стремится удалиться от Земли. Объект в точке В испытывает меньшее ускорение, чем Земля, то есть он тоже стремится удалиться от нее, но в противоположную сторону (➙ рис. 2.4).

Рис. 2.4 – Приливные силы
Приливная сила достигается с учетом относительного ускорения объекта по отношению к Земле, которое является следствием притяжения Луны: в точке А объект испытывает большее ускорение, чем Земля (➙ рис. 2.3), то есть стремится от нее удалиться. В точке В объект испытывает меньшее ускорение, чем Земля (➙ рис. 2.3), то есть тоже стремится удалиться от Земли, но в противоположную сторону.
Отметим, что здесь не представлена сила земного притяжения, которая не дает океанам устремиться в мировое пространство во время приливов и отливов.
Чтобы вычислить силу, воздействующую на Землю, достаточно умножить ускорение на массу объекта (F→; = ma→;): полученные силы, которые стремятся «разорвать» Землю на части, называются приливными силами.
Приливные силы действуют на любые объекты на поверхности Земли: в частности, на воду океанов. Таким образом, океаны образуют две «возвышенности» на поверхности Земли: один находится там, где Луна в зените, другой на противоположной стороне Земли. В этих точках уровень воды наиболее высок: здесь наблюдается прилив.
Но через шесть часов Земля совершит четверть оборота вокруг своей оси. Человек, находившийся на «возвышенности», оказывается во «впадине»: наступает отлив. Таким образом, в одной и той же точке Земли за сутки происходит два прилива и два отлива.
Под воздействием приливных сил океан мог бы улететь в мировое пространство. Но нужно учесть и земное притяжение, действующее на воду океанов. Оно уравновешивает приливные силы.
Следует отметить, что Солнце также вызывает приливы на Земле по тем же причинам. В сущности, это объясняет явление высоких и низких приливов.
Луна создает две возвышенности в точках-антиподах. Солнце делает то же самое. Поэтому, если два светила находятся по одну сторону Земли (новолуние) или по разные ее стороны (полнолуние), их воздействие объединяется, поскольку возвышенности, создаваемые обоими светилами, находятся в одном месте: когда возвышенности довольно значительны, это высокий прилив (➙ рис. 2.5).
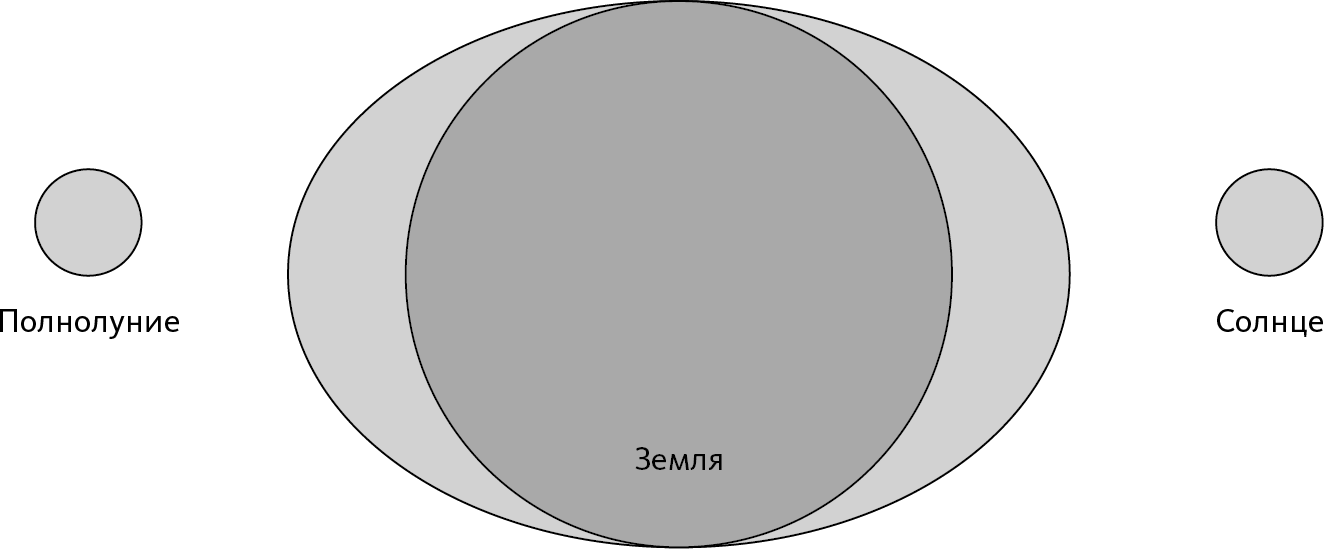
Рис. 2.5 – Приливы во время полнолуния
Если же Солнце и Луна находятся по отношению друг к другу под углом 90°, отлив, вызванный одним светилом, имеет ту же силу, что и прилив, вызванный другим. То есть двойное воздействие частично гасит друг друга: это вызывает низкий прилив (➙ рис. 2.6).
Луна совершает оборот вокруг Земли за 28 дней, и мы наблюдаем примерно по два высоких и два низких прилива каждый месяц (высокие приливы происходят в новолуние и полнолуние, низкие – в первую и последнюю четверть).

Рис. 2.6 – Приливы первой четверти Луны
Выше мы упоминали, что приливные силы стремятся «разорвать» Землю на части. Так, океаны были бы унесены в космос, если бы их не удерживала гравитация.
Между тем приливные силы действуют в Солнечной системе повсюду, где есть два взаимодействующих тела. И может случиться так, что гравитация не сможет компенсировать «выталкивающую» силу прилива.
Так происходит с естественным спутником, когда он оказывается очень близко к своей планете: приливные силы, вызываемые этой планетой, будут очень сильны. До определенного расстояния, называемого пределом Роша, приливные силы превышают силу притяжения, которая удерживает спутник: спутник «раскалывается» (то есть в пределах этой зоны спутник существовать не может).
Это объясняет кольца Сатурна: они находятся внутри предела Роша, и материя не может сформировать здесь большой спутник. Она распределена по орбите в виде «булыжников». Кроме того, эта материя наверняка была принесена крупным планетоидом, который подлетел к планете слишком близко и был разрушен приливными силами…
Спутник Юпитера Ио также не далек от предела Роша. Более того, периодическое влияние других спутников то приближает, то отдаляет его от планеты. Таким образом, мощные приливные силы то уменьшают, то увеличивают то, что сильно давит на спутник. Результатом этого является постоянная вулканическая деятельность на Ио, выброс избыточной внутренней энергии, образованной этими трениями.
Вернемся к нашей системе Земля-Луна, чтобы описать заключительное последствие действия приливных сил. Если приливные силы Луны действуют на Землю, действие приливных сил Земли по отношению к Луне еще более значительно. Если бы Луна была очень твердым телом, на ней не образовывалось бы выпуклостей. Но планеты и их спутники всегда подвержены некоторой деформации: из-за приливных сил они своей формой напоминают мяч для регби (как видно на рис. 2.7).
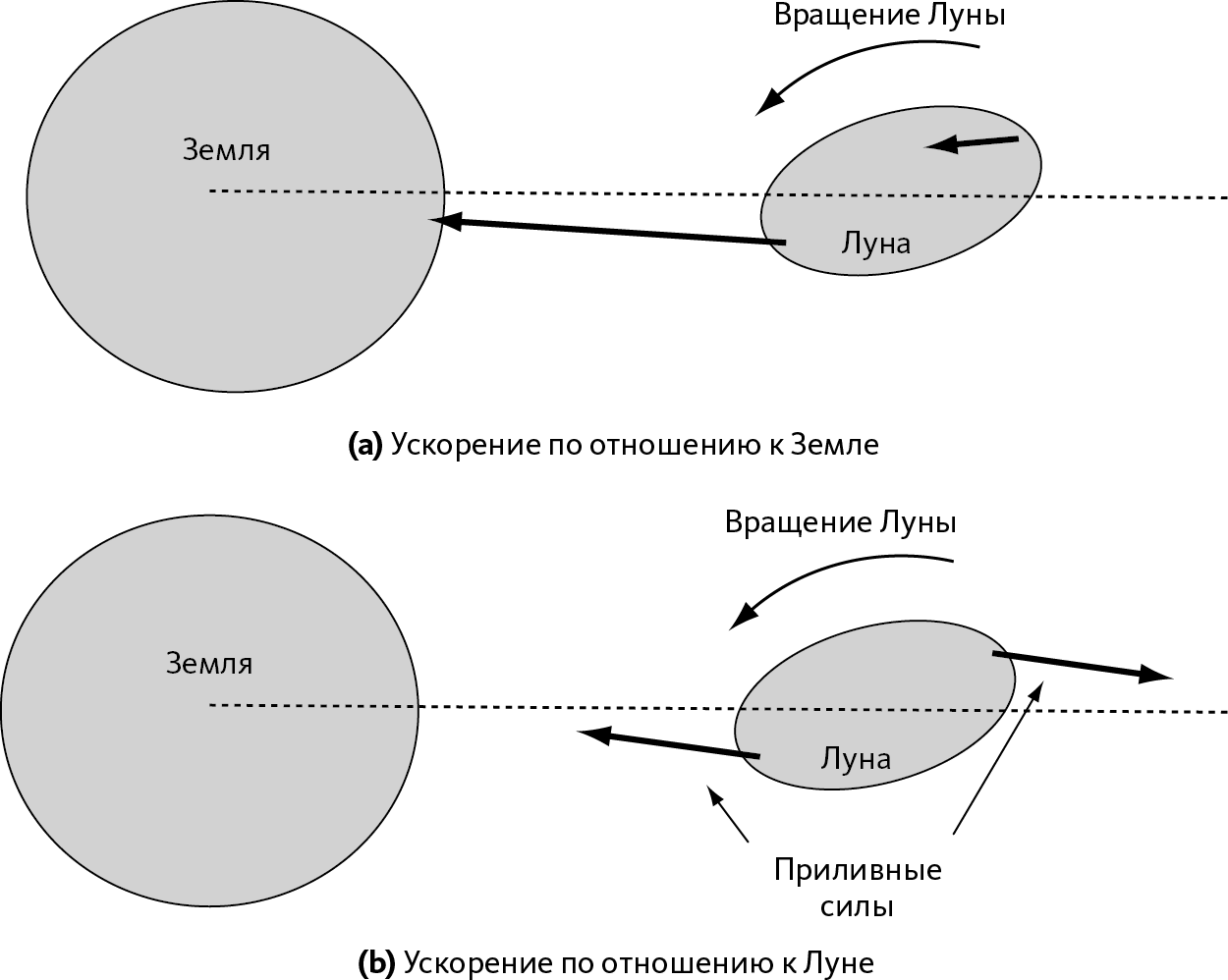
Рис. 2.7 – Влияние приливов на скорость вращения тела
Луна превратилась в мяч для регби из-за приливных сил; но благодаря инерции выпуклости достигают своей максимальной амплитуды, когда Земля уже не в зените (или в точке-антиподе), из-за вращения Луны.
В геоцентрической системе отсчета (а) ускорение, оказываемое на выпуклости, направлено в сторону Земли, а потому наклонено в сторону пунктирной оси. Ускорение, действующее на центр Луны, направлено вдоль оси. «Индивидуальное» ускорение выпуклостей по отношению к Луне направлено к пунктирной оси (b). Мы видим, что приливные силы противостоят вращению Луны в дополнение к тому, что стремятся ее разрушить.
Представим, что Луна очень быстро вращается вокруг своей оси. Поверхность вращается, а выпуклости по-прежнему обращены к Земле (и ее точкам-антиподам): а значит, эти выпуклости расположены не всегда в одном и том же месте лунной поверхности. Иными словами, выпуклости перемещаются по Луне.
Из-за действия инерции проходит довольно длительное время, прежде чем лунные горы разрушаются и формируют выпуклость. То есть образование выпуклости происходит с опозданием: когда выпуклость достигает максимальной амплитуды, Земля уже не в зените.
Из этого следует, что выпуклости направлены не совсем в сторону Земли, как показано на рис. 2.7. Мы также изобразили приливные силы, действующие на уровне этих выпуклостей, и видим, что из-за этого отклонения они не только стремятся «разрушить» Луну, но и препятствуют ее вращению. Такая Луна мало-помалу будет вращаться все медленнее из-за действия приливных сил.
В конечном итоге этот феномен действует до тех пор, пока скорость вращения Луны вокруг своей оси не будет равна ее скорости вращения вокруг Земли, а в этом случае Луна будет повернута к Земле всегда одной и той же стороной. Выпуклости больше не будут опаздывать, потому что всегда будут расположены на том же месте Луны: приливные силы больше не стремятся замедлить лунное вращение.
Именно это и произошло в истории системы Земля-Луна: Луна постепенно замедлила вращение вокруг своей оси, и теперь мы постоянно видим одну и ту же ее поверхность. Подобный феномен свойствен всем крупным спутникам в Солнечной системе.
Приливные силы Луны действуют также и на Землю, а потому с Землей происходит ровно то же самое. Иными словами, вращение Земли вокруг своей оси мало-помалу замедляется из-за приливных сил Луны. Во времена динозавров сутки длились меньше 24 часов.

СЛЕДУЕТ ЗАПОМНИТЬ
• Сила притяжения пропорциональна массам двух взаимодействующих тел и обратно пропорциональна квадрату расстояния между двумя телами.
• Все тела, испытывающие притяжение одного и того же тела, подвержены равному ускорению. Такова специфическая особенность силы притяжения.
• Два тела, испытывающие гравитационное взаимодействие, действуют друг на друга с одинаковой силой.
• Вес является частным случаем силы притяжения вблизи поверхностей планет. Он равен произведению массы объекта на поле тяготения, также называемое ускорением свободного падения, которое зависит от радиуса и массы планеты и представляет собой ускорение тела в свободном падении.
• Гравитационная постоянная выражает коэффициент силы притяжения для двух тел массой 1 кг на расстоянии 1 м и является одной из фундаментальных констант физики.
• Приливные силы, возникающие из-за силы притяжения, действующей на спутник: точки на поверхности спутника испытывают разное ускорение, поскольку расположены на разном расстоянии от тела. То есть на эти точки действует определенная сила. Эта сила стремится «расчленить» спутник вдоль оси, связывающей ее с телом.
• Приливные силы объясняют не только приливы на Земле, но также и кольца Сатурна, вулканизм Ио, а также то, что Луна всегда обращена к нам одной и той же стороной.
3. Электростатическая сила
Пора обратить наше внимание на вторую основополагающую силу Вселенной: электромагнитную силу. В связи с этим нам представится возможность погрузиться в мир бесконечно малого, после того как мы с силой притяжения рассматривали мир бесконечно большого.
На первый взгляд электромагнитная сила выглядит сложнее силы притяжения, и в этой главе мы ограничимся простым примером: когда частицы, создающие эту силу, остаются в пределах определенной системы отсчета. Речь идет об «электростатической силе»: слово «магнитный» исчезло, потому что условием неподвижности частицы является отсутствие магнетизма.
Магнетические аспекты будут рассмотрены в следующей главе: эта тема немного сложнее. Более того, мы с некоторой относительностью убедимся, что магнетические аспекты есть не что иное, как частое проявление электростатической силы.
Электростатика сама по себе невероятно сильно влияет на нашу жизнь и окружающую среду: она управляет нашей повседневностью в гораздо большей степени, чем гравитация.
1. Описание электростатической силы
Первые наблюдения
Влияние электростатической силы на нашу жизнь кажется нам редким, а то и вовсе не существующим, но на самом деле, чтобы ее увидеть, нужно ее создать.
Первые наблюдения за этим явлением принадлежат грекам: они обратили внимание, что, если потереть янтарь, он будет притягивать предметы, а иногда даже пускать искры. Так была открыта новая сила, притягивающая на расстоянии.
Следует отметить, что она явно не связана с гравитацией, поскольку это касается объектов, чья масса чересчур мала для гравитационного взаимодействия.
Первичный опыт можно проделать с пластмассовой линейкой, если потереть ее о шерстяной свитер, при этом желательно, чтобы воздух был довольно сухой: линейка будет притягивать малейший клочок бумаги, который приклеится к ней. В таких случаях мы говорим, что линейка «наэлектризована». В сухую погоду происходит то же самое, когда вы снимаете шерстяной свитер, ваши волосы трутся об него, слышится треск, а в темноте можно увидеть искры, похожие на те, которые заметили древние греки.
Но систематические опыты в этом направлении начнут проводиться только в эпоху Возрождения. Подвергнув трению различные вещества, исследователи пришли к выводу: два идентичных наэлектризованных вещества отталкиваются, различные наэлектризованные вещества иногда притягиваются, иногда отталкиваются.
Дальнейшие наблюдения позволили разделить наэлектризованные вещества на две разные категории: с положительным зарядом и с отрицательным. Два вещества с одинаковым зарядом отталкиваются, вещества с разными зарядами притягиваются.
Происхождение этих «зарядов» в то время было тайной. Казалось, что подобно массе заряд является неким свойством, присущим объекту, но, в отличие от массы, заряд можно создать или погасить с помощью трения.
Взаимодействие заряженных объектов
Чтобы создать более сильное трение, мы вращали шары с большой скоростью и обнаружили, что вещество получило более мощный заряд, то есть:
• шары сильнее притягивали и отталкивали другие наэлектризованные предметы: по аналогии с гравитацией мы назовем это: более высокий «активный заряд»;
• они сильнее притягивались и отталкивались другими наэлектризованными предметами: тут мы говорим о более высоком «пассивном заряде».
Проделаем следующий опыт: прикрепим два одинаковых шара на пружины к горизонтальной опоре друг против друга (➙ рис. 3.1). При помощи трения зарядим оба шара, придав левому шару заряд более сильный. Поскольку шары сделаны из одного материала, они будут отталкиваться, имея одинаковый заряд (например, положительный). Вопрос в том, какая пружина сжата сильнее или на какой из шаров действует бóльшая сила.

Рис. 3.1 – Отталкивание двух шаров с разной силой зарядов
Ответ очевиден – длина пружин абсолютно одинакова, что означает, что обе силы равны: воздействие предметов друг на друга уравновешивается:
• более мощный активный заряд левого шара стремится сильнее оттолкнуть правый шар;
• более мощный пассивный заряд правого шара заставляет его сильнее отталкиваться от левого шара.
Из этого опыта мы заключаем, что активный и пассивный заряды одного предмета равны. В дальнейшем мы будем говорить просто о «заряде», без дополнительных уточнений. Мы также будем говорить просто о «силе взаимодействия», не уточняя, на какой из двух объектов она действует, поскольку оба они испытывают одну и ту же силу.
Подведем итог: электростатическая сила пропорциональна заряду притягивающего (или отталкивающего) объекта и заряду притягиваемого (или отталкиваемого) тела.
На данном этапе очевидна связь с наблюдениями за гравитацией, что не может не вызывать интерес… Но на этом аналогия не заканчивается! Опыт показывает, что эта сила уменьшается пропорционально квадрату расстояния между двумя телами: как и в случае с гравитацией, если расстояние умножить на десять, сила уменьшится в сто раз.

ЕЩЕ ОДНА СИЛА, ДЕЙСТВУЮЩАЯ НА РАССТОЯНИИ
Мы объяснили действие на расстоянии силы притяжения существованием маленьких частиц-посланников – гравитонов, которые передвигаются от одного тела к другому. Это, в свою очередь, объясняло ослабление силы пропорционально квадрату расстояния.
То же самое справедливо и для электростатической силы! Только здесь частицы, испускаемые заряженным телом, называются фотонами. Фотоны не так скрытны, как гравитоны: нам предстоит убедиться, что фотоны являются частицами, из которых состоит свет и все прочие электромагнитные излучения. Эти частицы прекрасно видны: теоретически это единственные частицы, которые мы можем видеть, ибо речь идет о свете, который бросается нам в глаза!
Учитывая, что фотоны выявлены лучше других частиц, и учитывая аналогию между гравитацией и электростатикой, начинаешь лучше понимать, почему физики так уверены в существовании гравитонов, хотя они пока так и не были обнаружены…
Сила большой мощности
Продолжим аналогии, сравнив мощность электростатической силы и силы притяжения. Достаточно простого примера: линейка, «слабо» наэлектризованная вашим свитером, притягивает к себе клочки бумаги, чего не происходило до того, пока в ней не возник заряд, а это значит, что электростатическое притяжение во много раз превосходит силу гравитации между линейкой и бумагой.
Более того, опыт показывает, что вес бумаги меньше электростатической силы, поскольку клочки бумаги остаются подвешенными к линейке, не падая с нее. То есть всей огромной массы Земли недостаточно, чтобы уравновесить слабый разряд линейки, притянувшей бумагу.

ВЫРАЖЕНИЕ ЭЛЕКТРОСТАТИЧЕСКОЙ СИЛЫ
Сделанные нами наблюдения позволяют вывести формулу электростатической силы. Такая сила, исходящая от тела с зарядом Q и воздействующая на тело с зарядом q на расстоянии d, будет выражена как 
Величина k является коэффициентом мощности силы для определенного заряда и расстояния. По сути, это аналог гравитационной постоянной G, но существенная разница между ними в том, что k не имеет названия. По некоторым причинам, которые было бы слишком сложно здесь объяснять, физики считают, что  ε0 является фундаментальной константой электростатики и называется диэлектрической проницаемостью вакуума.
ε0 является фундаментальной константой электростатики и называется диэлектрической проницаемостью вакуума.
Иными словами, электростатическая сила не просто мощнее, она полностью «подавляет» силу гравитации, которая рядом с ней выглядит смехотворно. Почему же электростатическая сила столь незаметна во Вселенной? Потому что не существует или существует слишком мало объектов, заряженных так, чтобы мы могли это заметить. Почему так мало объектов имеют заряд, если все они имеют массу? На этот ключевой вопрос мы попытаемся ответить в дальнейшем.
Остается рассмотреть влияние электростатической силы на движение объектов. И здесь появляется фундаментальное различие с силой притяжения. Уравнение a→; = F→;/ m поможет нам это понять.
Оно означает, что ускорение объекта зависит от его массы (= от его инертности) и от силы, действующей на него. Между тем электростатическая сила в том числе зависит от заряда объекта. Так, чем мощнее заряд и чем меньше масса объекта, тем сильнее будет его ускорение. Таким образом, при взаимодействии с одним и тем же заряженным телом два различных объекта будут иметь разное ускорение.
В случае с гравитацией ее сила пропорциональна массе объекта, что уравновешивалось его инертностью: при взаимодействии с одним и тем же массивным телом два различных объекта будут иметь одинаковое ускорение.
И вот перед нами величайшая тайна: почему ускорение объекта, на который действует только электростатическая сила, зависит от его массы, если масса связана с гравитацией, а не с электростатикой? Внимательный читатель заметит, что речь идет о тайне гравитационной и инертной масс, но в несколько другом аспекте.
Итак, есть гравитационная составляющая (масса) в электростатическом взаимодействии, но нет никакого составляющего электростатики (нет заряда) в гравитационном взаимодействии. Откуда же такое отличие?
Другое существенное отличие: заряженные тела могут притягиваться или отталкиваться в зависимости от знака их заряда, в то время как массивные тела могут только притягиваться, потому что все массы обладают одним знаком. Но куда же подевались объекты с отрицательной массой?
Невзирая на эти различия и нестыковки, между двумя силами все-таки существует сильная связь, и невольно хочется думать, что обе они суть проявление некой единой силы, управляющей Вселенной. Как мы указывали во введении, можно понять, почему объединение двух основополагающих сил в одну является одной из величайших целей физики XXI в.

ОТРИЦАТЕЛЬНАЯ МАССА ВО ВСЕЛЕННОЙ
Аналогии между электростатикой и гравитацией, естественно, заставляют нас задуматься о том, какой была бы Вселенная, в которой существовали бы положительная и отрицательная массы, подобно тому как существуют положительный и отрицательный заряды.
Тело с отрицательной массой все бы отталкивало, а тело с положительной массой все бы притягивало[3]. В итоге началась бы бесконечная гонка между положительными массами, убегающими от отрицательных, которые они притягивают[4].
С другой стороны, в случае с отрицательной массой два тела с одинаковым знаком массы притягивались бы, а с противоположным знаком отталкивались бы, что создавало бы огромное количество тел с одинаковым знаком массы, которые свели бы на нет всю гравитацию.
В подобной вселенной не могла бы сформироваться планета, на которой есть жизнь. Так что не стоит жалеть, что в нашей вселенной отрицательной массы не существует.
Если электростатическая сила кажется настолько мощной по сравнению с гравитацией, видимое отсутствие в природе заряженных тел делает из нее силу, которая кажется почти анекдотической. Все дело в том, что мы рассматриваем ее не в том масштабе.
Как мы видели, сила притяжения становится ощутимой только в случае с телами значительной массы, такими как планеты, их естественные спутники и звезды. Именно поэтому в предыдущем разделе мы заострили внимание на крупных объектах, то и дело обращаясь к открытому космосу.
Однако с электростатической силой все обстоит наоборот: она проявляет себя на микроскопическом уровне. Однако микроскопический мир, несмотря на всю его близость, очень мало знаком нам, ибо мы не можем наблюдать его невооруженным глазом (в отличие от Луны, Солнца и звезд). Вот почему мы совершим небольшой обзор мира малых величин, который нас окружает, чтобы понять, почему электростатическая сила является вездесущей.