Это база: Зачем нужна математика в повседневной жизни - читать онлайн

2 Как политики выбирают своих избирателей

Древние греки много чего подарили миру: поэзию, драму, скульптуру, философию, логику. Кроме того, они дали нам геометрию и демократию, которые, как оказалось, связаны между собой теснее, чем кто-либо мог предположить, и меньше всего сами греки. Конечно, политическая система Древних Афин представляла собой очень ограниченную форму демократии – голосовать могли только свободные мужчины, но не женщины и не рабы. Так или иначе, в эпоху наследных правителей, диктаторов и тиранов афинская демократия была заметным шагом вперед. Как и греческая геометрия, которая в изложении Евклида Александрийского подчеркивала, как важно делать базовые предположения ясными и четкими, а все остальное выводить из них строго логически и системно.

Но как математика может использоваться в политике? Политика – это сфера человеческих отношений, соглашений и обязательств, а математика – это холодная абстрактная логика. В политических кругах риторика берет верх над логикой, а бездушные математические расчеты кажутся очень далекими от политических споров. Но демократическая политика подчиняется правилам, а у них бывают следствия, которые не всегда можно предвидеть, когда правила вводятся. Новаторские работы Евклида по геометрии, собранные в его знаменитых «Началах», установили стандарт того, как нужно делать выводы из правил. Фактически это неплохое определение математики в целом. В любом случае сегодня, всего лишь через 2500 лет, математика начинает проникать и в политический мир.

Как ни странно, в условиях демократии политики, на словах преданные идее о том, что решения должен принимать «Народ», всеми силами стараются не допустить этого. Такая тенденция восходит к той самой первой демократии в Древней Греции, где право голоса давалось только мужчинам-афинянам, составлявшим около трети взрослого населения. Одновременно с зарождением идеи выбирать руководителей и направления политики путем народного голосования появилась еще более привлекательная идея подмять под себя этот процесс и взять под контроль тех, кто голосует, и результаты голосования. Это несложно, даже когда каждый избиратель имеет один голос, потому что результаты голосования зависят от контекста, в котором оно происходит, а контекст всегда можно подтасовать. Как деликатно выражается профессор журналистики Уэйн Докинз, в итоге политики начинают выбирать своих избирателей, а не избиратели политиков{6}.

Вот здесь-то и вступает в игру математика. Не в политических дебатах, а в структуре правил этих дебатов и в контексте, в котором они проводятся. Математический анализ – обоюдоострое оружие. Он может открывать новые, хитроумные методы подтасовки голосов, а может и выявлять подобную практику, указывать на ее свидетельства и способствовать предотвращению.

Кроме того, математика подсказывает, что в любой демократической системе должны присутствовать элементы компромисса. Невозможно получить все, что вы хотите, каким бы желанным это ни было, поскольку список желаемого всегда внутренне противоречив.

Газета The Boston Gazette подарила 26 марта 1812 года миру новое слово: джерримандер (gerrymander), что означало манипуляции с нарезкой избирательных округов. Первоначально это слово писалось через дефис – «джерри-мандер» – и было результатом словослияния, которым впоследствии широко пользовался Льюис Кэрролл, то есть сложения частей двух общеизвестных слов. Часть «мандер» представляла собой концовку слова «саламандра», а часть «джерри» – концовку имени Элбриджа Джерри, губернатора штата Массачусетс. Точно неизвестно, кто первым сложил две концовки вместе, но историки считают, что это был один из редакторов газеты: Натан Хейл, Бенджамин Рассел или Джон Рассел.

Что же такого сделал Элбридж Джерри, что его имя навсегда соединилось с названием похожего на ящерицу существа, жившего, согласно средневековому фольклору, в огне? Подтасовал результаты выборов.

Говоря точнее, именно Джерри протолкнул закон, изменивший границы избирательных округов в Массачусетсе на выборах в сенат штата. Деление на избирательные округа, как это называют, естественным образом связано с определением границ. Это обычное дело и сегодня, и в давние времена для большинства демократий. Очевидная причина деления на округа – практические соображения: неудобно принимать решения, если по каждому предложению должна голосовать вся страна. (Наглядный пример – Швейцария: до четырех раз в год федеральный совет отбирает предложения для голосования граждан и устраивает, по существу, серию референдумов. При этом женщины там не имели права голоса до 1971 года, а один из кантонов даже продержался до 1991 года.) Существует освященная временем традиция избирать всеобщим голосованием сравнительно небольшое число представителей и уже этим представителям давать право принимать решения. Один из наиболее справедливых методов – пропорциональное представительство, когда число представителей той или иной политической партии пропорционально числу полученных ею голосов. Чаще всего население разбивают на округа, и каждый округ избирает определенное число представителей, примерно пропорциональное числу избирателей в нем.

Например, на президентских выборах в США каждый штат голосует за определенное число «выборщиков» – членов коллегии выборщиков. Выборщики имеют по одному голосу, и кто станет президентом, определяется простым большинством их голосов. Эта система появилась в те времена, когда доставить сообщение из американской глубинки в центр можно было лишь верхом или в экипаже, запряженном лошадьми. Железнодорожные магистрали и телеграф появились позже. В те дни процесс подсчета голосов громадного числа людей шел слишком медленно{7}. Но эта система, помимо прочего, передавала контроль в руки членов коллегии выборщиков. В случае британских парламентских выборов страна делится (в основном географически) на избирательные округа, каждый из которых выбирает одного члена парламента. Затем партия (или коалиция партий), получившая максимальное число мест в парламенте, формирует правительство и выдвигает одного из своих членов парламента на пост премьер-министра. Премьер-министр Великобритании обладает значительными полномочиями и во многом напоминает президента.

Существует еще одна скрытая причина для передачи процедуры принятия демократических решений в руки небольшого числа «проводников»: так проще манипулировать голосами. Все подобные системы имеют внутренние недостатки, которые часто приводят к странным результатам, а при случае ими можно воспользоваться, чтобы игнорировать волю народа. В наши времена уже не раз на президентских выборах в США полное число голосов избирателей, отданных за проигравшего кандидата, было больше, чем у победившего кандидата. Хотя нынешний метод выборов президента не зависит от воли избирателей, при современных средствах коммуникации единственная причина, по которой США не переходят на более справедливую систему, видится в том, что многих власть имущих устраивает именно такой вариант.

Основная проблема здесь – «бесполезные голоса». В каждом штате кандидату для победы нужна половина общего числа проголосовавших плюс один голос (или полголоса, если общее число нечетное). Голоса, полученные сверх этого порога, никак не влияют на то, что происходит на этапе работы коллегии выборщиков. Так, на президентских выборах 2016 года Дональд Трамп получил 304 голоса выборщиков, а Хиллари Клинтон – 227 голосов, но число проголосовавших за Клинтон избирателей было на 2,87 млн больше, чем у Трампа. Так что Трамп стал пятым президентом США, получившим этот пост при проигранном общенародном голосовании.

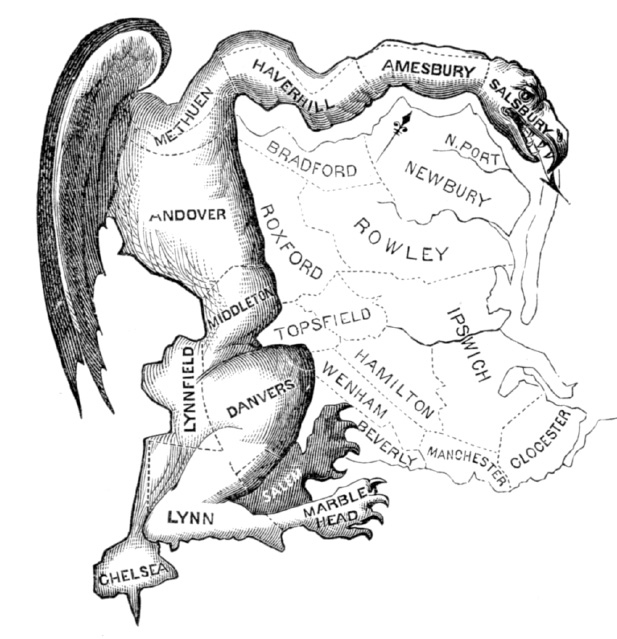
Джерримандер – подтасовка голосов по рецепту Джерри. Считается, что эту карикатуру нарисовал в 1812 году Элкана Тисдейл

Границы американских штатов практически неизменны, так что проблемы манипуляции ими нет. А вот внутри границы округов могут изменяться, причем обычно это делает партия, находящаяся у власти, и здесь проявляется еще более коварный порок системы. Дело в том, что партия может проводить границы таким образом, чтобы гарантировать конкурирующей партии потерю необычно большой доли голосов. Возьмем Элбриджа Джерри и выборы в сенат. Когда массачусетские избиратели увидели карту избирательных округов, они не заметили почти ничего необычного. Однако один из округов заметно отличался от остальных. Он объединял 12 административных районов запада и севера штата и имел сложную форму. Политическому карикатуристу, автору рисунка, который вскоре появился в The Boston Gazette, – скорее всего, это был художник, дизайнер и гравер Элкана Тисдейл, – этот округ показался очень похожим на саламандру.

Джерри принадлежал к Демократической республиканской партии, конкурировавшей в то время с Федералистской партией. На выборах 1812 года федералисты завоевали палату представителей штата и пост губернатора, в результате чего Джерри остался без места. Однако проведенное им разбиение на округа на выборах в сенат штата позволило Демократической республиканской партии одержать победу.

Математика манипуляций по рецепту Джерри начинается с анализа того, как они делаются. Существуют две основные тактики разбиения на округа: концентрация и распыление. При концентрации ваши собственные голоса распределяются как можно равномернее для получения небольшого, но решающего большинства в как можно большем числе округов, а остальные округа сдаются врагу. Прошу прощения, оппозиции. Распыление предполагает разбивку голосов оппозиции так, чтобы она проиграла в как можно большем числе округов. Пропорциональное представительство, при котором число представителей пропорционально полному числу голосов, полученному каждой партией (или предельно близко к нему), позволяет избежать подобных фокусов и является более справедливым. Неудивительно, что Конституция США делает пропорциональное представительство незаконным, потому что, согласно ей, каждый округ должен иметь только одного представителя. В 2011 году Великобритания провела референдум по другой альтернативе, системе единого передаваемого голоса: народ проголосовал против предлагавшихся изменений. Референдума по пропорциональному представительству в Великобритании никогда не было.

Нарезка избирательных округов в Джерримандии. Вверху слева: 50 районов следует разделить на пять округов по 10 районов в каждом. Предпочтения избирателей (голосуют они за Темную или за Светлую партию) отражены на карте оттенком серого. Вверху справа: концентрация дает Светлым три округа, а Темным только два. Внизу слева: распыление отдает Темным все пять округов. Внизу справа: такое разбиение обеспечило бы пропорциональное представительство

Вот как работают концентрация и распыление в вымышленном примере с очень простой географией и столь же простым распределением голосов.

В государстве Джерримандия за власть борются две политические партии, Светлые и Темные. В этом государстве 50 районов, которые следует распределить по пяти избирательным округам. На недавних выборах Светлые получили большинство в 20 северных районах, тогда как Темные имели большинство в 30 южных районах (рис. вверху слева). Правительство Светлых, которые с минимальным перевесом победили в предыдущем голосовании, изменило границы избирательных округов, обеспечив большинство своих сторонников в трех округах (вверху справа), так что теперь Светлые побеждают в трех округах, а Темные получают только два. После этого Темная партия оспаривает изменение границ в суде на том основании, что форма и границы новых избирательных округов с очевидностью говорят о подтасовке, и умудряется получить контроль над изменением границ перед следующими выборами. Темные используют метод распыления (внизу слева), чтобы обеспечить себе победу во всех пяти избирательных округах.

Если избирательные округа должны состоять из 10 небольших квадратных районов каждый, лучшее, что могут получить Светлые методом концентрации, это три округа из пяти. Им необходимо выиграть выборы в шести районах из 10, чтобы победить в округе в целом, а всего они контролируют 20 районов. Это дает им три шестерки плюс еще два района, которые оказываются бесполезными. Лучшее, чего могут добиться Темные методом распыления, – это получить все пять округов. Пропорциональное представительство дало бы Светлым два округа, а Темным – три, как показано на рисунке внизу справа. (На практике пропорциональное представительство не достигается разбиением на избирательные округа.)

Страны с диктаторским или близким к нему режимом в большинстве своем проводят выборы, чтобы показать миру, насколько они демократичны. Результаты этих выборов обычно подтасовываются, и даже если их разрешено оспорить в суде, разбирательства никогда не бывают успешными из-за небеспристрастности судов. В демократических странах можно не только опротестовать изменение границ избирательных округов, но и выиграть дело, потому что суды не зависят от правящей партии. Если, конечно, судьи не назначаются по партийной принадлежности.

В подобных случаях основная проблема, с которой сталкиваются судьи, носит неполитический характер. Все упирается в поиск объективного способа, позволяющего определить, имела ли место подтасовка. На каждого «эксперта», который посмотрит на карту и заявит, что видит явный случай подтасовки, всегда найдется другой «эксперт», который придет к противоположному выводу. Необходимы более объективные методы, чем личное мнение и словесные аргументы.

Здесь определенно нужна математика. Формулы и алгоритмы позволяют количественно оценивать разумность и справедливость границ округов и выявлять их необъективность в четко определенном смысле. Сама по себе разработка этих формул и алгоритмов не объективный процесс, конечно, но, как только они становятся общепринятыми (а это отчасти процесс политический), каждый может воспользоваться ими и проверить результаты независимо. Это дает суду логическую основу для принятия решения.

Разобравшись в коварных методах, которые дают политикам возможность изменять границы избирательных округов в свою пользу, можно придумать математические критерии или правила, позволяющие распознавать применение этих методов. Ни одно подобное правило не может быть идеальным – более того, существует доказательство, что это невозможно, к которому я перейду, как только мы поймем суть правил. В настоящее время используются пять подходов:

• Выявление избирательных округов странной формы.

• Выявление несоответствия в соотношении получаемых мест и числа голосов.

• Оценка количества бесполезных голосов, создаваемого данным делением на округа, и его сравнение с тем значением, которое законно считается приемлемым.

• Анализ всех возможных конфигураций округов и оценка вероятного результата при каждой из них с точки зрения количества полученных мест на основе существующих данных об избирателях, чтобы понять, является ли предложенная карта статистической аномалией.

• Выработка процедур, гарантирующих, что итоговое решение будет справедливым, что его сочтут справедливым и что обе партии согласятся с его справедливостью.

Пятый подход – самый удивительный, но, как ни странно, его на самом деле можно реализовать. Рассмотрим эти подходы по очереди, оставив удивительное напоследок.

Во-первых, округа странной формы.

Еще в 1787 году Джеймс Мэдисон писал в «Записках федералиста», что «естественным пределом любой демократии является расстояние от центральной точки, которое позволит самым далеко живущим гражданам собираться так часто, как того требуют их общественные функции». Если воспринимать это буквально, он предлагал делать избирательные округа приблизительно круглыми и не настолько большими, чтобы время пути от периферии до центра было чрезмерным.

Предположим, например, что основную поддержку политическая партия получает в прибрежных районах. Включение всех живущих там избирателей в один округ приведет к тому, что округ получится длинным, узким и извилистым и будет тянуться вдоль всего побережья. Это совершенно неестественно в сравнении с остальными компактными и разумными по форме округами. Нетрудно прийти к выводу, что здесь происходит что-то подозрительное, а границы проведены так, чтобы сделать бесполезными как можно больше голосов избирателей этой партии. Странная форма перекроенных избирательных округов часто свидетельствует о манипуляциях, как это было в случае необычного округа губернатора Джерри.

Правоведы могут спорить до умопомрачения о том, какую именно форму следует считать странной. Поэтому в 1991 году юристы Дэниел Полсби и Роберт Поппер предложили способ количественной оценки необычности формы, известный сегодня как тест Полсби – Поппера{8}. Он вычисляется по формуле:

Человек, хоть немного знакомый с математикой, сразу обратит внимание на множитель 4π. Подобно приятелю Вигнера, который не понимал, как численность населения связана с окружностями, мы можем спросить, какое отношение окружности имеют к политическим играм с избирательными округами. Ответ необычайно прост и прямолинеен: круг – самая компактная из геометрических фигур.

Этот факт имеет давнюю историю. Согласно древнегреческим и древнеримским источникам, а именно поэме Вергилия «Энеида» и «Филипповой истории» Гнея Помпея Трога, основательницей города-государства Карфагена была царица Дидона. Историческое повествование Трога кратко пересказал Юниан Юстин в III веке, и в его рассказе мы находим поразительную легенду. Дидона и ее брат Пигмалион были наследниками неназванного царя города Тира. После смерти царя народ хотел, чтобы им правил Пигмалион, несмотря на юный возраст. Дидона вышла замуж за своего дядю Акербаса, который, по слухам, обладал несметными сокровищами. Пигмалион захотел получить эти сокровища, а потому убил Акербаса. Дидона сделала вид, что выбросила его сокровища в море, хотя на самом деле утопила просто мешки с песком. Опасаясь, вполне разумно, гнева Пигмалиона, она бежала сначала на Кипр, а затем на северное побережье Африки. Там Дидона обратилась к берберскому царю Ярбу с просьбой выделить небольшой участок земли, где она могла бы пожить какое-то время. Тот ответил, что разрешает ей забрать себе столько земли, сколько удастся окружить бычьей шкурой. Дидона разрезала шкуру на тонкие полоски и охватила ими близлежащий холм, который до сего дня носит название Бирса, что значит «шкура». Основанное там поселение стало городом Карфагеном, и, когда он вырос и разбогател, Ярб сказал Дидоне, что она должна выйти за него замуж – или ее город будет разрушен. Дидона принесла множество жертв на громадном костре, сделав вид, что хочет почтить таким образом своего первого мужа и подготовиться к браку с Ярбом, затем взошла на костер, сказала, что скорее присоединится к первому мужу, чем уступит притязаниям Ярба, и пронзила себя мечом.

Мы не знаем, существовала ли Дидона на самом деле (хотя Пигмалион определенно существовал, и в некоторых источниках наряду с ним упоминается и Дидона). Поэтому говорить об исторической точности этой легенды бессмысленно. Как бы то ни было, в исторической легенде кроется легенда математическая: Дидона использовала шкуру, чтобы окружить холм, выложить из ремешков окружность вокруг него. Почему окружность? Потому что – как утверждают математики – она знала, что именно окружность охватывает максимально большую площадь для заданного периметра{9}. Этот факт носит впечатляющее название «изопериметрическое неравенство». Он был известен еще в Древней Греции, но строгое доказательство получил только в 1879 году, когда математик Карл Вейерштрасс заполнил пробел в пяти различных доказательствах, опубликованных геометром Якобом Штейнером. Штейнер доказал, что если оптимальная фигура существует, то это должна быть окружность, но он не сумел доказать ее существование{10}.

Изопериметрическое неравенство гласит, что

Это применимо к любой плоской геометрической фигуре, у которой есть периметр и площадь. Более того, постоянная 4π – наилучшая из возможных (ее невозможно сделать больше), и вариант «больше или равно» превращается в равенство только в том случае, когда фигура – круг{11}. Именно изопериметрическое неравенство навело Полсби и Поппера на мысль о том, что величина, которую я назвал тестом Полсби – Поппера (ПП), может служить эффективным способом оценки округлости геометрической фигуры. Вот несколько примеров:

Для избирательного округа по Джерри ПП составляет примерно 0,25.

Однако у ПП есть серьезные недостатки. Необычные формы избирательных округов иногда бывают неизбежными из-за таких особенностей местной географии, как реки, озера, леса и очертания побережий. Более того, избирательный округ может быть аккуратным и компактным и при этом очевидно организованным с целью манипуляций. Так, карта избирательных округов на выборах 2011 года в законодательное собрание штата Пенсильвания выглядела очень причудливо и неестественно, и в 2018 году республиканцы подготовили предложения по ее изменению. Предложенные округа полностью соответствовали пяти параметрам, определенным Верховным судом штата, но математический анализ распределения голосов в округах показал, что границы все равно не были объективными и заметно влияли на результаты голосования.

Даже масштаб карты может вызвать проблемы. Основная из них – фрактальность геометрии. Фрактал – это геометрическая фигура с детальной структурой во всех масштабах. Многие природные формы больше похожи на фракталы, чем на евклидовы треугольники и окружности. Береговые линии и облака можно очень эффективно моделировать в виде фракталов, что позволяет отразить их замысловатую форму. Термин «фрактал» пустил в обращение в 1975 году Бенуа Мандельброт, разработавший и активно продвигавший новую область – фрактальную геометрию. Береговые линии и реки представляют собой чрезвычайно извилистые фрактальные кривые, и их длина при измерении сильно зависит от того, насколько мелкий масштаб при этом используется. На самом деле длина фрактальной кривой теоретически бесконечна, что в переводе на язык повседневной реальности звучит так: «Измеренная длина возрастает безгранично по мере того, как вы рассматриваете объект все в больших подробностях». Так что юристы могут спорить до бесконечности об измерении периметра, не говоря уже о том, был ли данный избирательный округ изменен с целью манипуляции.

Поскольку странность формы такой неточный параметр, имеет смысл попробовать что-нибудь более определенное. Соответствуют ли результаты голосования статистическим избирательным паттернам электората?

Если на выборах идет борьба за 10 мест, а симпатии избирателей распределяются 60:40, то можно ожидать, что шесть мест получит одна партия, а четыре – другая. Если же одна партия получит все 10 мест, то можно заподозрить подтасовку. Однако на самом деле все не так просто. Результат такого рода обычен в мажоритарных системах голосования. Так, во время всеобщих выборов 2019 года в Великобритании Консервативная партия получила 44 % голосов, но 365 из 650 мест, что составляет 56 % всех мест. Лейбористы получили 32 % голосов и 31 % мест. Шотландские националисты с 4 % голосов получили 7 % мест (хотя это особый случай, поскольку их избирательная база целиком находится в Шотландии). Либеральные демократы получили 12 % голосов и 2 % мест. Большая часть несоответствий здесь была следствием региональных избирательных паттернов, а не странно проведенных границ избирательных округов. В конце концов, если результат двухпартийных выборов одного человека, скажем президента, решается простым большинством, то 50 % голосов (плюс один голос) будет достаточно для получения поста целиком.

Вот американский пример. В штате Массачусетс на федеральных и президентских выборах с 2000 года республиканцы получали в целом более трети голосов. Тем не менее в последний раз республиканцы занимали в этом штате хотя бы одно место в палате представителей аж в 1994 году. Подтасовка? Похоже, нет. Если эта треть республиканских избирателей распределена по территории штата более или менее равномерно, то, как бы вы ни проводили границы округов – исключая экстремальные варианты, при которых границы огибают дома отдельных граждан, – доля сторонников Республиканской партии в каждом округе составит приблизительно одну треть. Демократы победят везде. Именно так и происходило все эти годы.

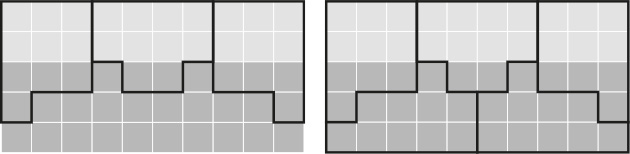
Слева: предложение Светлых, при котором границы двух округов оставлены на усмотрение Темных. Справа: наиболее компактный вариант, который Темные могли бы выбрать

Во время одних реальных выборов математики показали, что такой эффект может оказаться неизбежным, как ни проводи границы, по крайней мере если не делить на части отдельные городки. В 2006 году, когда Кеннет Чейз боролся против Эдварда Кеннеди на выборах в сенат США, Массачусетс был разделен на девять избирательных округов. Чейз получил 30 % голосов, но проиграл во всех девяти округах. Компьютерный анализ вариантов показал, что ни один набор городов, объединенных в округ, даже если брать города, разбросанные по территории штата произвольным образом, не принес бы Чейзу победу. Его сторонники были распределены по большинству городов довольно равномерно, и обеспечить ему победу не удалось бы, какие границы ни проведи.

В уже знакомой нам Джерримандии, когда Темные выиграли во всех пяти округах, Светлые опротестовали это деление на округа на основании того, что прямоугольные округа получились слишком длинные и узкие, так что Темные, очевидно, занимались распылением. Суд постановил, что округа должны быть более компактными. Светлые разработали схему трех компактных округов и великодушно предложили Темным самим решить, как разделить еще на два округа оставшиеся территории. Темные запротестовали, потому что такое разбиение отдавало Светлым три округа, а Темным оставляло только два, хотя сторонников у них было больше.

Это деление показывает еще два недостатка использования критерия компактности как средства обнаружения манипуляций. Хотя деление и компактно, оно все равно отдает Светлым 3/5 округов при наличии у них всего 2/5 голосов. К тому же не существует способа разбить оставшиеся территории на два компактных округа. Из-за особенностей географии в Джерримандии трудно добиться компактности и справедливости одновременно. А может быть, и невозможно, в зависимости от определений.

Поскольку критерий компактности небезупречен, подумаем, как еще можно распознать деление на округа в пользу одной из партий. Данные голосования говорят нам не только об исходе выборов, но и о том, что было бы, если бы распределение полученных сторонами голосов сдвинулось на определенную величину. Например, если бы при голосовании в каком-то округе было отдано 6000 голосов за Темных и 4000 за Светлых, то Темные выиграли бы. Если бы 500 избирателей перебежали от Темных к Светлым, то Темные все равно выиграли бы, но если бы мнение изменил 1001 избиратель, то Темные проиграли бы. Если бы голоса распределились как 5500 за Темных и 4500 за Светлых, то достаточно было бы переманить всего 501 избирателя, чтобы изменить результат. Короче говоря, по данным голосования в округе можно узнать не только о том, кто победил, но и о том, насколько близки результаты соперников.

Можно выполнить этот расчет для каждого округа, собрать результаты воедино и посмотреть, как распределение полученных мест меняется со сдвигом голосов, и получить кривую места-голоса. (На самом деле это ломаная линия с множеством прямолинейных участков, но для удобства ее сглаживают.) Рисунок слева показывает, как приблизительно должна выглядеть такая кривая для неподтасованных выборов. В частности, эта кривая должна пересекать 50 %-ный порог для мест при 50 %-ном распределении голосов, и она должна быть симметричной по обе стороны от этой точки при повороте на 180º.

На рисунке справа показана кривая места-голоса для карты округов во время выборов в конгресс штата Пенсильвания, при этом на горизонтальной оси отложены голоса Демократической партии. Демократам требовалось около 57 % голосов, чтобы получить 50 % мест. Эта карта впоследствии была изменена решением законодательного собрания штата.

В нескольких случаях Верховный суд США отверг обвинения в манипуляциях, сделанные на основании подобных расчетов, как, впрочем, и обвинения, основанные на недостаточной компактности округов. В деле LULAC v. Perry 2006 он все же принял решение об изменении некоторых границ избирательных округов в Техасе на том основании, что границы одного из округов противоречили Закону об избирательных правах. Хотя Верховный суд и объявил изменение избирательных округов в пользу одной из партий неконституционным, он фактически не отменил целиком ни одной карты округов.

График зависимости распределения мест от числа голосов. На горизонтальной оси отложен процент голосов, отданных за одну партию (показан интервал от 30 до 70 %). Вертикальная ось показывает процент мест, которые партия получила бы с таким количеством голосов

Главная причина, которую суд привел в обоснование своего отказа, состояла в том, что методы вроде кривой места-голоса построены на гипотетических предположениях относительно поведения избирателей в иных обстоятельствах. Возможно, для юристов это звучит убедительно, но математически это чепуха, поскольку кривая строится на основе реальных данных по голосованию и по точно определенной процедуре. Перенос голосов при расчете кривой не зависит от того, как конкретный избиратель может поступить в реальности. Это как посмотреть на счет в баскетбольном матче и сказать, что при счете 101:97 игра, должно быть, шла на равных, а при счете 120:45 – нет. Вы при этом не делаете предположений о том, как могли бы повести себя отдельные игроки, если бы играли лучше или хуже. Так что этот момент можно добавить к длинному и ничем не примечательному списку случаев неспособности закона понять или хотя бы просто оценить простую математическую логику. Якобы гипотетический характер этого совершенно строгого и основанного на фактах алгоритма служит предлогом для отказа от изменения карты избирательных округов Техаса.

В случае сомнительных юридических решений бесполезно поучать судей, поэтому сторонники математических методов распознавания манипуляций занялись поисками других показателей и критериев, которые невозможно отбросить по надуманным основаниям. Манипуляции заставляют сторонников одной из партий бесполезно тратить значительное количество голосов. Как только ваш кандидат получает большинство, все дополнительные голоса становятся лишними и никак не влияют на результат. А раз так, то при справедливом выборе границ избирательных округов обе партии должны тратить бесполезно примерно одинаковое число голосов. В 2015 году Николас Стефанопулос и Эрик Макги нашли новый метод подсчета бесполезных голосов – анализ разрыва в эффективности{12}. В деле Gill v. Whitford 2016 суд Висконсина объявил карту избирательных округов на выборах в законодательное собрание штата незаконной, и основанием для этого решения стал разрыв в эффективности. Чтобы посмотреть, как вычисляется разрыв в эффективности, упростим процесс до выбора из двух кандидатов.

Существует два основных способа сделать ваш голос бесполезным. Голос, отданный за проигравшего кандидата, бесполезен потому, что вы могли с тем же успехом не голосовать вообще. Лишний голос, отданный за победителя уже после того, как он набрал 50 %, бесполезен по той же причине. Справедливость этих утверждений зависит от реальных результатов и определяется задним числом: невозможно с уверенностью сказать, что ваш голос бесполезен, пока неизвестны результаты выборов. В ходе всеобщих выборов 2020 года в Великобритании кандидат от лейбористов в моем избирательном округе получил 19 544 голоса, а кандидат консерваторов – 19 143 голоса. Лейборист победил с перевесом в 401 голос при общем числе голосов, отданных за две партии, равном 38 687. Если бы какой-то избиратель решил не голосовать, перевес все равно составил бы 400 голосов. Но если бы от голосования воздержалось чуть больше 1 % сторонников Лейбористской партии, победил бы кандидат консерваторов.

Согласно определению, бесполезными у Консервативной партии стали все 19 143 голоса, а у Лейбористской партии – 200 голосов. Разрыв эффективности показывает, насколько у одной партии бесполезных голосов больше, чем у другой. В данном случае он равен:

То есть (19 143–200)/38 687, что составляет +49 %.

И это всего один избирательный округ. Идея метода в том, чтобы рассчитать совокупный разрыв в эффективности для всех избирательных округов и добиться, чтобы законодатели установили целевое значение. Разрыв в эффективности всегда лежит между –50 % и +50 %, а справедлив разрыв, равный 0 %, поскольку в этом случае у обеих партий бесполезными оказывается одинаковое число голосов. В итоге Стефанопулос и Макги предложили считать, что разрыв в эффективности, выходящий за рамки ±8 %, указывает на манипуляции.

Однако и у этого способа измерения есть недостатки. Когда результаты близки, большой разрыв в эффективности неизбежен, и всего несколько голосов могут изменить его с почти +50 до почти –50 %. В моем избирательном округе манипуляций не было, несмотря на разрыв в эффективности +49 %. Если бы всего 201 человек, вместо того чтобы отдать голос лейбористам, проголосовал за консерваторов, он был бы равен –49 %. Если одной из партий просто везет и она побеждает в каждом округе, кажется, будто это результат манипуляций. Демографические факторы также могут искажать картину. В деле Gill v. Whitford защита справедливо указала на эти недостатки, но истцы заявили, что к данному случаю они отношения не имеют, и выиграли дело. Однако в целом такие возражения совершенно оправданны.

В 2015 году Майра Бернштейн и Мун Дучин{13} нашли у разрыва в эффективности еще ряд недостатков, а в 2018 году Джеффри Бартон показал, как можно устранить их{14}. Предположим, например, что у нас есть восемь округов и в каждом из них Светлые получают 90 голосов, тогда как Темным достаются оставшиеся 10. У Светлых при этом бесполезных голосов 40 × 8 = 320, а у Темных – 10 × 8 = 80, так что разрыв в эффективности составляет (320–80)/800 = 0,3 = 30 %. Если принять предложенный 8 %-ный порог, то такой разрыв в эффективности говорит о манипуляциях, направленных против Светлых. Но Светлые по результатам голосования получили все восемь мест!

Второй сценарий вскрывает еще один вопрос. Предположим, что Светлые побеждают в трех округах 51:49, тогда как Темные – в двух с таким же результатом 51:49. Тогда у Светлых пропадает 1 + 1 + 1 + 49 + 49 = 101 голос, а у Темных 49 + 49 + 49 + 1 + 1 = 149 голосов. Разрыв в эффективности составляет (101–149)/500 = –0,096 = –9,6 %, что говорит о манипуляциях против Темных. Однако Темные – партия меньшинства, ей не следует рассчитывать больше чем на два места, что они и делают. Получение Темными еще одного места дало бы партии меньшинства большую часть мест.

Слева: график зависимости числа мест от числа голосов показывает пропорциональное представительство (жирная линия) и область (выделена серым), в которой разрыв в эффективности считается справедливым. Справа: график модифицированного разрыва в эффективности: серая область окружает диагональную линию

Бартон объясняет обе проблемы использованием необработанных данных о бесполезных голосах. На любых выборах голоса сверх необходимого, отданные за победителя, пропадают напрасно, какими бы ни были границы округов. Бартон заменяет «бесполезные голоса» на «голоса, пропадающие без необходимости», вычисляя для каждой партии долю голосов, которые однозначно пропадут, и вычитая их из бесполезных голосов. При первоначальном определении график места-голоса дает узкую полосу вокруг линии, идущей от 25 % голосов внизу до 75 % наверху, как на рисунке слева. Диагональная линия показывает идеальный график для пропорционального представительства. То и другое совпадает лишь на очень небольшом участке вблизи распределения голосов 50:50. Если учитывать голоса, пропадающие без необходимости, то получается график, показанный справа. Здесь область приемлемого разрыва в эффективности плотно окружает диагональ, что, конечно, куда более разумно.

Еще один метод распознавания манипуляций заключается в рассмотрении альтернативных карт и сравнении гипотетических результатов с использованием данных о вероятных паттернах распределения голосов по всему региону, о разбивке которого на округа идет речь. Если карта, предложенная Темными, дает им 70 % мест, а большинство альтернативных карт – лишь 45 %, то они явно мухлюют.