Алгоритмы для жизни: Простые способы принимать верные решения - читать онлайн

Каждый год влюбленные парочки студентов-первокурсников возвращаются после совместных каникул по случаю Дня благодарения, разругавшись в пух и прах. Это так часто происходит, что у психологов колледжей есть даже специальное словечко: turkey drop.

Однажды к психологу на прием пришел Брайан, крайне возбужденный первокурсник. Его школьная подружка уехала учиться в другой колледж, и теперь у них был классический роман на расстоянии. Кроме того, их мучил непростой философский вопрос: а хорошие ли у них отношения? Сравнивать им было не с чем. Психолог посочувствовала Брайану, сказала, что это типичная дилемма первокурсников, и невозмутимым тоном предложила удивительное: «Собирай данные».

Сторонники серийной моногамии, как правило, сталкиваются с фундаментальной неизбежной проблемой. Когда можно считать, что вы познакомились с достаточным количеством людей, чтобы найти свою половинку? А что, если вы уже пропустили ее? Настоящая «уловка-22» в любовных делах!

Ответ на крик души этого влюбленного первокурсника содержится в теории, которую математики называют «задачей об оптимальной остановке». И звучит он так: 37 %.

Ну или как-то иначе. Все зависит от ваших взглядов на любовь.

Задача о секретаре

В любой задаче об оптимальной остановке критически важный вопрос – не «какой вариант необходимо выбрать», а «как много вариантов необходимо рассмотреть и учесть». Эти задачи имеют значение не только для влюбленных или арендаторов, но и для водителей, домовладельцев, грабителей и т. д.

Правило 37 %[2] произошло от самой известной головоломки об оптимальной остановке, которая со временем стала известна как «задача о секретаре». Исходные данные задачи очень напоминают дилемму о поиске квартиры, которую мы рассматривали ранее. Представьте, что вы проводите собеседование с рядом кандидатов на позицию секретаря и ваша цель – выбрать и принять на работу единственного кандидата, лучшего из всех. Пока у вас нет представления, как распределить баллы между каждым из претендентов, вы можете легко определить, кому вы отдаете предпочтение. (В этом случае математик сказал бы, что вы оперируете только порядковыми числами – вы сравниваете только соответствующие качества, которыми обладают все кандидаты. Но вам недоступны количественные числа – вы не можете ранжировать эти качества в общей шкале.) Вы интервьюируете претендентов в произвольном порядке, по одному за раз. Вы можете принять решение нанять кандидата в любой момент собеседования, а он, в свою очередь, примет ваше предложение и завершит свои поиски работы. Но при этом, если вы упустите кандидата, решив не нанимать его, вы потеряете его навсегда.

Считается, что задача о секретаре впервые была опубликована (без непосредственного упоминания секретарей) в февральском номере журнала Scientific American в 1960 году Мартином Гарднером в качестве одной из головоломок в его популярной колонке о занимательной математике. Однако само происхождение задачи остается загадкой. Наше собственное расследование с нуля привело нас к некоторой гипотезе еще до того, как оно неожиданно превратилось для нас в детективную работу в прямом смысле слова. Мы отправились в Стэнфорд, чтобы в архивах работ Гарднера найти его переписку середины прошлого века. Чтение писем немного напоминает подслушивание чужого телефонного разговора: вы слышите только одну сторону диалога, а ответ можете лишь предположить. В нашем случае у нас были только ответы на вопросы, которыми, очевидно, задавался сам Гарднер более 50 лет назад, исследуя историю происхождения задач. Чем больше мы читали, тем более запутанной и неясной казалась нам эта история. Гарвардский математик Фредерик Мостеллер вспомнил, что слышал об этой задаче в 1955 году от своего коллеги Эндрю Глизона, который, в свою очередь, слышал о ней от кого-то еще. Лео Мозер из Альбертского университета рассказывал в своем письме, что читал о головоломке в «неких записях» Р. И. Гаскелла из компании Boeing, который приписывал авторство задачи своему коллеге. Роджер Пинкхам из Ратгерского университета писал, что впервые услышал о головоломке в 1955 году от математика по фамилии Шонфильд из Университета Дьюка, а тот, по его убеждению, сам впервые услышал о задаче от кого-то из Мичигана. Этот «кто-то из Мичигана», с большой вероятностью, носил имя Меррил Флад. И хотя за пределами мира математики его имя мало кому известно, влияние Флада на развитие компьютерной науки нельзя не отметить. Именно он обратил внимание на задачу о коммивояжере (которую мы обсудим более подробно в главе 8), изобрел математическую игру «Два бандита» (которая будет описана в главе 11) и даже, весьма вероятно, ввел термин «программное обеспечение». По его же собственным словам, Флад приступил к изучению вопроса в 1949-м и в 1958 году стал автором своего первого известного открытия – правила 37 %. Хотя он и отдает пальму первенства в этом вопросе другим математикам.

Достаточно будет отметить, что вне зависимости от своего происхождения задача о секретаре оказалась едва ли не идеальной математической загадкой: ее легко объяснить, очень сложно решить, решение ее чрезвычайно лаконично, а выводы крайне занимательны. В результате она передавалась из уст в уста в математических кругах в 50-е годы, распространяясь со скоростью лесного пожара, и только благодаря Гарднеру и его колонке в 1960 году захватила воображение широкой общественности. К 80-м задача и различные ее вариации столько раз подвергались анализу, что ее стали обсуждать в газетах как подраздел самой себя.

А что до секретарей, довольно умилительно наблюдать, как каждая культура накладывает свой особый антропологический отпечаток на формальные системы. К примеру, при мысли о шахматах нам представляется средневековая Европа, хотя на самом деле появились шахматы в VIII веке в Индии. Они были достаточно грубо «европеизированы» в XV веке, когда «шахи» были переименованы в «королей», «визири» – в «королев», а «слоны» стали «офицерами».

Аналогичным образом менялись и задачи об оптимальной остановке, отражая насущные проблемы и переживания каждого поколения. В XIX веке типичными ситуациями для таких задач были барочные лотереи или выбор подходящего поклонника для дамы; в начале XX века – поиск лучшего отеля для автопутешественника и выбор подходящей спутницы для мужчины; в середине XX века, во время расцвета офисной рутины и доминирования мужчин, – подбор лучшей секретарши для руководителя-мужчины. Впервые название задачи о секретаре именно в такой формулировке было упомянуто в газете в 1964 году, позднее оно закрепилось окончательно.

Почему 37 %?

Подбирая секретаря, вы можете совершить две ошибки: остановиться либо слишком рано, либо слишком поздно. Если вы прекращаете поиски рано, существует большой риск, что лучшего кандидата вы еще не успели встретить. Если останавливаетесь слишком поздно, вы продолжаете ждать идеального кандидата, которого не существует. Оптимальная стратегия требует от вас баланса между чрезмерным и недостаточным поиском.

Если ваша цель – найти лучшего претендента и вы не согласны на меньшее, то очевидно, что, пока вы проводите собеседования с кандидатами, вы не должны даже позволять себе мысли нанять кого-то, если он не лучший из всех, кого вы видели. Тем не менее просто быть лучшим недостаточно для того, чтобы получить предложение о работе. Ведь самый первый кандидат будет лучшим просто по определению. Проще говоря, совершенно очевидно, что показатели «лучшего на данный момент» претендента будут снижаться от собеседования к собеседованию. Например, второй кандидат имеет шансы 50 на 50 стать лучшим из тех, что вам довелось встретить. Но у пятого кандидата есть уже только один шанс из пяти, а у шестого – один из шести. В итоге «лучшие на данный момент» претенденты неизменно будут все больше впечатлять вас по мере продолжения поиска (ведь они по определению уже лучше всех тех, кто приходил до них), однако и попадаться они будут все реже и реже.

Хорошо, теперь мы знаем, что принимать на работу первого «лучшего на данный момент» кандидата (иначе говоря, самого первого кандидата) – опрометчивое решение. Если у вас есть сто претендентов, поспешным будет предложить работу и второму «лучшему на данный момент» только потому, что он лучше первого. Так как же действовать?

Существует несколько потенциальных стратегий. Например, нанять кандидата, который в третий раз превосходит всех, кого вы уже видели. Или даже четвертый. Или, возможно, стоит принять следующего «лучшего на данный момент» кандидата после долгой «засухи» – вереницы слабых игроков. Но на поверку ни одна из этих относительно разумных стратегий не оказывается на высоте. Наоборот, оптимальное решение приобретает формы того, что мы называем правилом «семь раз отмерь, один раз отрежь». Вы изначально определяете количество таких «замеров», в нашем случае это рассмотрение вариантов и сбор информации, в течение которого вы не останавливаете свой выбор ни на ком, как бы он или она вас ни впечатлили. После этого вы переходите на этап «отрежь», когда вы готовы принять на работу любого, кто затмит лучшего кандидата, увиденного вами на первом этапе.

Мы можем наблюдать, как вырисовывается правило «отмерь и отрежь» даже при совсем маленьком количестве кандидатов на позицию секретаря в нашей задаче. У вас есть всего один кандидат? Решение простое – наймите его! Если у вас два претендента, ваши шансы на успех 50 на 50, что бы вы ни предприняли. Вы можете нанять первого претендента (который проявил себя лучше всех из первой половины прошедших собеседование) или же можете отказаться от первого и по умолчанию выбрать второго (который впечатлил вас больше всего из второй половины претендентов). Добавим третьего кандидата, и здесь уже становится интересней. Наш шанс на успех в этом случае равняется 33 %. При наличии двух кандидатов мы могли полагаться только на удачу. Но если их трое, возможно, мы можем сами принять правильное решение?

Получается, что можем. И все зависит от того, как мы поступим со вторым проинтервьюированным претендентом.

Когда мы встречаем первого кандидата, у нас нет никакой информации, и, разумеется, он или она окажутся по умолчанию лучшим вариантом. Когда мы беседуем с третьим кандидатом, у нас нет свободы выбора, поскольку мы, в конце концов, должны кого-то нанять, а остальные кандидатуры мы уже отклонили. Но, когда мы встречаемся со вторым претендентом, мы оказываемся посередине: мы можем оценить, лучше или хуже второй кандидат, чем первый, и одновременно у нас есть выбор – принять этого кандидата или отказать.

Что же произойдет в том или ином случае?

Мы рассмотрим лучшую из возможных стратегий на примере с тремя кандидатами. Этот подход работает на удивление удачно как с тремя претендентами, так и с двумя (в этом случае вам необходимо выбирать лучшего половину всего времени, предусмотренного на поиски[3]).

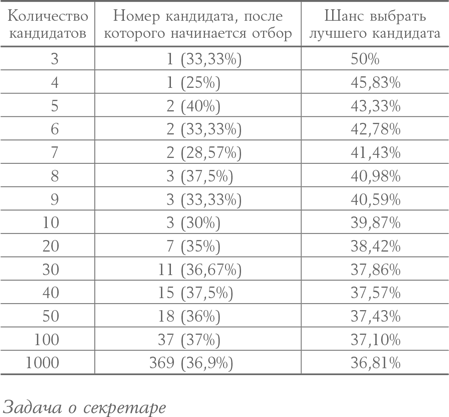
Если развивать этот сценарий до четырех претендентов, то отбор необходимо начинать со второго кандидата. При пяти претендентах – с третьего. По мере того как количество претендентов растет, провести эту черту необходимо на отметке 37 % от общего числа кандидатов, прежде чем начать отбор. Тщательно рассмотрите кандидатуры первых 37 % претендентов[4], не отдавая предпочтение ни одному из них. Затем будьте готовы выбрать первого, проявившего себя лучше всех рассмотренных до него.

Как оказывается, следование оптимальной стратегии в конечном итоге дает нам 37 %-ный шанс принять на работу лучшего кандидата. Одновременно в этой цифре заключается и уникальная математическая симметрия этой задачи: число, определяющее стратегию, и процент вероятности успеха совпадают. В таблице выше рассмотрены оптимальные стратегии для решения задачи о секретаре при различном количестве претендентов, при этом очевидно, что показатель вероятности успеха и точка отсчета для начала отбора кандидатов приближаются к отметке 37 % при возрастании общего количества кандидатов.

63 %-ная вероятность неудачи при использовании лучшей имеющейся стратегии – отрезвляющий факт. Даже если, решая задачу, мы будем действовать оптимально, все равно в большинстве случаев мы потерпим неудачу и, значит, нам не суждено принять на работу того самого лучшего кандидата.

Это плохая новость для тех, кто живет только поисками «того единственного (той единственной)». Но есть и положительный момент. Интуиция могла бы нам подсказать, что наши шансы на выбор лучшего кандидата будут неизменно уменьшаться при возрастании общего количества претендентов. Если бы мы искали наугад, выбирая, к примеру, из ста претендентов, у нас был бы лишь один шанс на успех. Из тысячи – 0,0001 % шанса. Тем не менее удивительно, что математическая составляющая задачи неизменна. При оптимальной остановке ваш шанс выбрать лучшего кандидата из ста – 37 %. И если выбирать из тысячи, то вероятность успеха по-прежнему 37 %. Таким образом, чем больше становится число претендентов, тем бóльшую ценность для нас может представлять знание алгоритма.

Действительно, в большинстве случаев вы вряд ли найдете потерянную иголку. Но оптимальная остановка, по крайней мере, защитит вас от ее поисков в стоге сена.

Любовный алгоритм

Задолго до того, как стать профессором в области операционных исследований в Университете Карнеги – Меллон, Майкл Трик был обычным выпускником и искал любовь. «Меня осенило: эта проблема уже изучена; это же задача о секретаре! У меня была свободная позиция и несколько претенденток и была цель – выбрать лучшую». Майкл произвел расчет. Он не знал, сколько женщин он встретит в своей жизни, но само по себе правило тридцати семи процентов обладает определенной гибкостью: его можно применить как в отношении количества кандидатов, так и при определении периода поиска. Трик предположил, что будет искать суженую с 18 до 40 лет. Таким образом, согласно правилу 37 % он определил, что по достижении 26,1 года он должен перейти от «просмотра» кандидаток к непосредственному отбору. Так и получилось. Поэтому, когда он встретил женщину, которая подходила ему больше всех тех, с кем он раньше встречался, он точно знал, что нужно действовать. Он сделал свой выбор.

«Я не знал, была ли она идеальна для меня (сама модель алгоритма не позволяет определить это), но, вне всяческих сомнений, она соответствовала всем параметрам для следующего шага. Я сделал ей предложение, – пишет Трик, – и она ответила мне отказом».

Математики не понаслышке знают о несчастной любви как минимум с XVII века.

Имя легендарного астронома Иоганна Кеплера по сей день остается на слуху благодаря открытию эллиптической формы планетных орбит и его огромной роли наравне с Галилеем и Ньютоном в «Революции Коперника», которая перевернула представление человека о его месте в космосе. Но у Кеплера были и вполне земные переживания. После смерти первой жены в 1611 году он приступил к долгим и непростым поискам второй половины. В общей сложности Кеплер ухаживал за одиннадцатью женщинами.

Из первой «четверки» больше всех ему нравилась четвертая кандидатка («из-за ее высокого роста и атлетического телосложения»), однако на ней он не прекратил свои поиски. «Вопрос был бы решен, – писал он, – если бы любовь и разум не подтолкнули бы ко мне пятую женщину. Она покорила меня своей любовью, скромной преданностью, экономностью в хозяйстве, кротостью и заботой, которую она дарила моим детям. И тем не менее я продолжил поиски».

Друзья и знакомые Кеплера представляли его все новым дамам, и он продолжал свой поиск, но с некоторым безразличием. Его мысли оставались с той пятой женщиной. В конечном счете, после одиннадцати ухаживаний, он решил прекратить поиски. «Готовясь к поездке в Регенсбург, я вернулся к пятой женщине, открылся ей и получил ее согласие». Кеплер и Сюзанна Рюттингер поженились и вырастили шестерых детей, включая его детей от первого брака. Биографии описывают семейную жизнь Кеплера и Сюзанны как самое спокойное и радостное время в его жизни.

И Кеплер, и Трик – хоть и с разными конечными результатами – первыми убедились на собственном опыте, что задача о секретаре излишне упрощает поиски второй половины. В классическом варианте задачи претенденты на должность всегда дают положительный ответ на предложение о работе, исключая отказ, с которым столкнулся Трик. А «вернуть» кандидата, как это получилось у Кеплера, не представляется возможным.

На протяжении десятилетий, с момента появления задачи о секретаре, ученые рассматривали множество вариантов развития сценария и в итоге разработали новые стратегии оптимальной остановки в различных условиях. Возможность получения отказа, к примеру, может быть устранена простым математическим решением – необходимо предлагать рано и часто. Предположим, если ваши шансы быть отвергнутым составляют 50 на 50, тот же математический анализ, с помощью которого появилось правило тридцати семи процентов, предписывает нам начать делать предложения после первой четверти ваших поисков. В случае отказа продолжайте делать предложения каждому «лучшему на данный момент» человеку, которого встречаете, пока не получите положительный ответ. С такой стратегией общая вероятность вашего успеха, то есть получение согласия на ваше предложение от лучшего кандидата из имеющихся, составит 25 %. Очевидно, это не такой уж и плохой расклад для сценария, в котором возможность получить отказ сочетается с общей сложностью определения прежде всего своих стандартов.

Кеплер, в свою очередь, открыто ругал себя за «тревожность и нерешительность», которые заставили его продолжить поиски. «Неужели не было иного способа для моего смятенного сердца примириться с судьбой, – жаловался он своему близкому другу, – кроме как осознать невозможность исполнения других моих желаний?» В этом случае теория оптимальной остановки вновь приносит некоторое утешение. Беспокойство и нерешительность уже в меньшей степени служат признаками моральной или психологической деградации и оказываются частью успешной стратегии в тех сценариях, где второй шанс возможен.

Если вы можете вернуть предыдущих претендентов, то оптимальный алгоритм существенно преображает знакомое нам правило «семь раз отмерь, один раз отрежь»: вы дольше можете не связывать себя обязательствами, и у вас есть резервный план. Например, предположим, что своевременное предложение обречено на положительный ответ, при этом запоздалые предложения отвергают через раз. В этом случае математический расчет призывает нас продолжать поиски без каких бы то ни было обязательств до тех пор, пока вы не просмотрите 61 % всех кандидатов, и затем выбрать из оставшихся 39 % того, кто окажется лучшим для вас. Если, рассмотрев хорошенько все варианты, вы по-прежнему остались одиноки, как было с Кеплером, то вернитесь к лучшему кандидату из прошлого. И даже в этом случае симметричность стратегии и результата сохраняется: при наличии возможности «войти в одну и ту же реку дважды» вероятность того, что вы остановите свой выбор на лучшем кандидате, снова составляет 61 %.

В случае Кеплера несоответствие между реальной жизнью и задачей о секретаре в ее классическом понимании привело его к счастливому концу. По сути, неожиданный поворот в классической задаче сыграл на руку и Трику. После того отказа он защитил диплом и получил работу в Германии. Там «он зашел в бар, влюбился в красивую женщину, через три недели они уже жили вместе. Он предложил ей пожить "некоторое время" в Штатах». Она согласилась, и спустя шесть лет они поженились.

Выбери лучшее с первого взгляда: полная информация

Первый рассмотренный нами набор вариантов – отказ и возврат – изменил в классической задаче о секретаре представление, что своевременные предложения принимаются всегда, а запоздалые – никогда. В этом случае наилучший подход остался таким же, как изначально: некоторое время наблюдать со стороны, взвесить все, а затем быть готовым к решительным действиям.

Но существует еще один важный момент в задаче о секретаре, который заставляет задуматься. А именно: мы ровным счетом ничего не знаем о соискателях, кроме их сравнительных характеристик. У нас нет четкого представления о том, каким должен быть хороший или плохой соискатель. Более того, когда мы сравниваем двух кандидатов, мы видим, кто из них лучше, но не понимаем, насколько лучше. И, проходя через эту неизбежную фазу поиска, мы рискуем упустить отличного кандидата, пока не определимся со своими требованиями и ожиданиями. Математики называют эту сложность с оптимальной остановкой игрой в отсутствие информации.

Этот принцип, вероятно, далек от большинства поисков квартиры, спутника жизни или того же секретаря. Но попробуйте на секунду представить, что у нас есть некий объективный критерий оценки (например, если бы каждый претендент на должность секретаря прошел бы обязательный экзамен на скорость печатания, результат которого выражался бы в перцентилях аналогично современным тестам SAT, GRE или LSAT). Таким образом, баллы каждого соискателя наглядно продемонстрируют его уровень среди всех прошедших тест: машинистка 51-го перцентиля всего лишь выше среднего уровня, в то время как машинистка 75-го перцентиля превосходит троих испытуемых из четырех и т. д.

Допустим, наша подборка соискателей репрезентативна и никоим образом не искажена и была выбрана случайно. Более того, предположим, что скорость печатания – это единственный критерий, по которому мы отбираем кандидатов на должность. Тогда мы приходим к тому, что математики называют полной информацией, и ситуация меняется. «Чтобы установить стандарт, не нужно накапливать опыт, – говорится в основной статье по этой проблеме, написанной еще в 1966 году, – и удачный выбор порой делается мгновенно». Иными словами, если соискателю 95-го перцентиля случается стать первым, кого мы оцениваем, мы мгновенно понимаем, что с уверенностью можем принять его на работу – при условии, конечно, что мы не рассматриваем наличие соискателя 96-го перцентиля в подборке.

И вот в чем загвоздка. Если опять же наша цель – найти наилучшего кандидата на должность, то нам по-прежнему необходимо взвесить вероятность существования более сильного претендента. Однако наличие у нас полной информации дает возможность вычислить эти шансы напрямую. Например, вероятность того, что следующий соискатель будет из 96-го перцентиля или выше, всегда будет 1 к 20. Таким образом, решение о том, когда следует прекратить поиски, сводится исключительно к тому, сколько еще кандидатов нам осталось просмотреть. Полная информация подразумевает, что нам не нужно так уж тщательно обдумывать свои действия. Вместо этого можно применить пороговое правило, руководствуясь которым мы можем немедленно принять на работу кандидата выше определенного уровня перцентиля. И нам не нужно просматривать первоначальную группу кандидатов, чтобы установить этот порог. Но стоит тем не менее учитывать, сколько еще соискателей остаются доступными.

Математика показывает, что, когда в подборке остается еще много кандидатов, легко пройти мимо хорошего претендента в надежде найти кого-то еще лучше. Но по мере уменьшения шансов вы должны быть готовы нанять того, кто окажется просто чуть выше среднего уровня. Это всем знакомое, хотя и не слишком вдохновляющее явление: в случае скудного выбора нам приходится снижать требования. Так же верно и обратное: если в море полно рыбы, то планку требований можно поставить выше. Но в обоих случаях, что особенно важно, именно математика говорит насколько.

Самый простой способ понять, как все это работает на практике, – попытаться начать с конца. Если вы дошли до последнего соискателя, то вам, конечно же, не остается ничего другого, кроме как принять его на работу. Но на собеседовании с предпоследним кандидатом вопрос уже ставится иначе: а выше ли он 50-го перцентиля? Если да, можете нанять его; если же нет, то стоит обратить внимание на последнего кандидата, поскольку его шансы оказаться выше 50-го перцентиля будут по определению равны 50/50. Аналогичным образом вам следует выбрать третьего от конца соискателя, если он окажется выше 69-го перцентиля, четвертого от конца – если он будет выше 78-го, и т. д. (будучи тем избирательнее, чем больше соискателей еще осталось). Но, несмотря ни на что, никогда не берите на работу кандидата ниже среднего уровня, если только ваше положение не совсем уж безвыходное. (И, поскольку вы все еще заинтересованы в выборе наилучшего человека из подборки, не стоит нанимать того, кто не превосходит просмотренных вами до сих пор соискателей.)

Шанс найти в итоге лучшего кандидата из всех возможных в этом варианте (при наличии полной информации) увеличивается до 58 % – что, конечно, далеко не гарантия успеха, но это значительно лучше тех 37 %, которые дает нам правило 37 % в игре без информации. И если у вас есть все факты, вероятность добиться своей цели выше, даже когда число претендентов произвольно растет.

Таким образом, игра с полной информацией приводит нас к неожиданному и, пожалуй, даже несколько странному заключению. Золотоискательство имеет гораздо больше шансов на успех, чем поиски любви. Если вы оцениваете своих потенциальных партнеров, основываясь на каком-либо объективном критерии (скажем, на перцентиле уровня их дохода), то вы получаете в свое распоряжение гораздо больше информации, чем в результате эфемерной эмоциональной реакции («любви»), которая требует как опыта, так и сравнительного анализа для принятия решения.

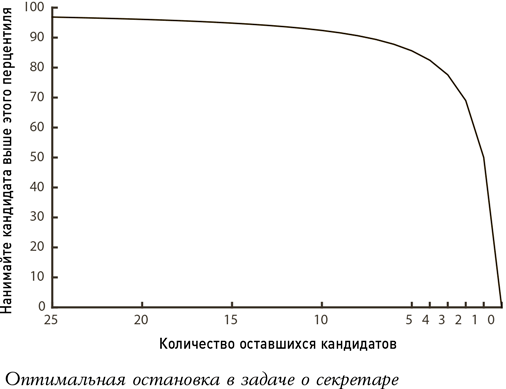
Конечно же, нет никаких оснований выбирать чистую стоимость активов – или, если на то пошло, скорость печатания – в качестве главного мерила. Любой показатель, дающий вам полное представление о том, насколько претендент соотносится с населением в целом, может изменить способ принятия решения с правила «семь раз отмерь, один раз отрежь» на пороговое правило, что резко повысит ваши шансы найти лучшего кандидата из всех предложенных.

Существует множество вариаций «проблемы секретаря», модифицирующих свойственные им условия в соответствии с такими более реальными задачами, как поиск спутника жизни (ну или секретаря). Но уроки, которые преподает нам оптимальная остановка, не ограничиваются одними лишь свиданиями или приемом на работу. На самом деле попытки сделать наилучший выбор в условиях, когда варианты предлагаются только по очереди, имеют место и в ситуации с продажей дома, парковкой автомобиля или принятием решения об уходе, будучи на пике успеха. И все эти проблемы в той или иной степени решаемы.

Когда продавать

Если мы изменим еще пару аспектов классической «проблемы секретаря», это перенесет нас из области знакомств и свиданий в сферу недвижимости. Ранее мы уже рассматривали процесс поиска съемной квартиры в качестве проблемы оптимальной остановки, но владение домом также не испытывает недостатка в оптимальной остановке.

Допустим, вы продаете дом. После консультаций с несколькими агентами по недвижимости вы выставляете его на продажу, освежаете слой краски на стенах, приводите в порядок лужайку и начинаете ждать предложений. Получив очередное предложение о покупке, вы, как правило, должны решить, принять ли его или отклонить. Но за отклоненные предложения приходится в итоге расплачиваться – еще одним еженедельным (или ежемесячным) платежом по ипотеке, пока вы ожидаете следующего предложения, вовсе не будучи уверенными в том, что оно будет выгоднее предыдущего.

Продажа дома похожа на игру с полной информацией. Мы знаем объективную долларовую стоимость всех предложений, которая позволяет нам не просто определить, какие из них выгоднее, но и понять, насколько они выгоднее. Более того, у нас есть довольно обширные сведения о состоянии рынка, что позволяет нам хотя бы приблизительно спрогнозировать диапазон цен в ожидаемых предложениях. (Это дает нам такую же информацию о перцентилях каждого предложения, какую мы рассматривали в примере с тестом на скорость печатания.) Однако наша цель уже не в том, чтобы выбрать наилучшее предложение, но в том, чтобы выручить как можно больше денег в рамках всей процедуры продажи в целом. Учитывая, что каждый день ожидания измеряется в долларах, есть смысл принять хорошее предложение прямо сейчас, а не ждать чуть более выгодного еще несколько месяцев.

Располагая данной информацией, мы можем не назначать примерный ценовой диапазон. Вместо этого мы установим четкий порог, будем игнорировать все, что ниже его, и примем то предложение, которое его превысит. Правда, если мы стеснены в средствах и они закончатся, если мы не продадим дом за определенный срок либо мы ожидаем получить весьма ограниченное число предложений и не особо заинтересованы в результате, то нам стоит снизить планку, так как подобный подход ограничивает. (Вот почему покупатели обычно ищут «мотивированных» продавцов домов.) Но если проблемы не загоняют нас в угол, мы можем просто сосредоточиться на анализе затрат и выгод игры в ожидание.

Сейчас мы разберем один из простейших случаев: мы точно знаем ценовой диапазон ожидаемых предложений, и все предложения в данном диапазоне равновероятны. Если нам нет нужды волноваться о том, что предложения (или наши сбережения) подойдут к концу, то мы можем сосредоточиться исключительно на расчетах, что мы приобретем или потеряем, если будем ждать более выгодной сделки. Если мы отклоним нынешнее предложение, то сможет ли вероятность более выгодного предложения, умноженная на ожидаемую нами разницу в выгоде, компенсировать связанные с ожиданием расходы? Как выясняется, математика здесь довольно проста, и мы видим прямую зависимость стоп-цены от цены ожидания следующего предложения.

Этот математический расчет не будет волновать нас, если мы продаем многомиллионный особняк или полуразвалившийся сарай. В этом случае будет иметь значение только небольшая разница между самой низкой и самой высокой ценой, которую нам, вероятно, предложат. Если мы введем конкретные цифры, то увидим, что данный алгоритм предлагает нам множество четких указаний. Допустим, ценовой диапазон ожидаемых нами предложений варьируется от $400 000 до $500 000. Если цена ожидания незначительна, мы можем быть почти бесконечно разборчивы. Если цена ожидания следующего предложения составляет всего $1, то мы получим максимальную выгоду, всего лишь дождавшись покупателя, который предложит нам за дом $499 572,99 и ни центом меньше. Если ожидание обойдется нам в $2000 за предложение, придется дотянуть до $480 000. В условиях медленного роста рынка, где ожидание будет стоить $10 000, нам придется принять любое предложение, которое превысит $455 279. Ну и наконец, если цена ожидания составит половину или даже больше от ожидаемого нами диапазона предложений (в данном примере это $50 000), то нет абсолютно никакого смысла тянуть дальше и нужно приложить максимум усилий, чтобы продать дом первому, кто назовет свою цену, и покончить с этим. Нищим выбирать не приходится.

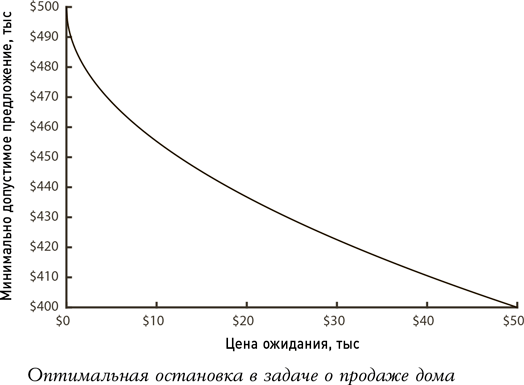
В данном примере важно отметить, что устанавливаемый нами предел зависит только лишь от стоимости поисков. Поскольку вероятность того, что следующее предложение окажется лучше предыдущего (а также стоимость выяснения этого) никогда не изменится, то нам нет смысла снижать стоп-цену, так как поиски продолжаются и не зависят от нашей удачливости. Мы устанавливаем ее однажды, прежде чем выставить дом на продажу, и в дальнейшем ориентируемся на нее.

Специалист по оптимизации Висконсинского университета в Мэдисоне Лора Альберт Маклей воспользовалась своими знаниями проблем оптимальной остановки, когда пришло время продавать ее собственный дом. «Первое же полученное нами предложение было замечательным, – рассказывает она, – но оно предполагало огромные затраты с нашей стороны, потому что покупатели просили нас съехать на месяц раньше, чем мы были к этому готовы. Было еще одно конкурентоспособное предложение… [но] мы держались, пока не получили подходящее нам». Многих продавцов необходимость отклонить парочку выгодных предложений весьма нервирует, особенно если последующие предложения уступают им в выгоде. Но Маклей твердо стояла на своем и сохраняла спокойствие. «Это было бы очень, очень тяжело, – признается она, – если бы я не знала, что математика на моей стороне».

Данный принцип применим к любой ситуации, где вам предстоит получить ряд предложений и заплатить за то, чтобы искать дальше или ждать следующего. Следовательно, это относится к случаям, которые выходят далеко за рамки продажи недвижимости. Например, экономисты, пользуясь этим алгоритмом, моделируют процесс поиска людьми работы и наглядно объясняют кажущийся на первый взгляд парадоксальным факт одновременного существования на рынке вакансий и безработных.

На самом деле, у этих вариаций проблемы оптимальной остановки есть еще одно поистине удивительное свойство. Как мы помним, возможность вернуть упущенный в прошлом шанс была жизненно важной в любовных поисках Кеплера. Но в случае с продажей дома или поисками работы вам никогда, ни в коем случае не следует так поступать, даже если есть возможность вернуться вновь к ранее отклоненному предложению и даже если это предложение все еще не утратило своей актуальности. Если оно не превышало ваш пороговый показатель на тот момент, оно не превысит его и сейчас. То, что вы заплатили за возможность продолжить поиски, – это невозвратные издержки. Не идите на уступки, не жалейте ни о чем. И никогда не оглядывайтесь.

Когда парковаться

Еще одна сфера, где в избытке имеется проблема оптимальной остановки и где бессмысленно сожалеть об упущенном шансе, – это все, связанное с автомобилем. Автомобилисты уже фигурировали в упомянутой нами проблеме секретаря, а современный стиль жизни, побуждающий постоянно двигаться вперед, превращает каждую поездку на машине еще и в проблему остановки: поиски ресторана; поиски туалета и, что наиболее остро для городских водителей, поиски парковочного места.

Кто лучше расскажет обо всех тонкостях парковки, чем заслуженный профессор Калифорнийского университета в Лос-Анджелесе по градопланированию Дональд Шоуп, которого Los Angeles Times назвала рок-звездой парковки? Мы ехали к нему на встречу из Северной Калифорнии, заверив Шоупа, что оставили в запасе достаточно времени для непредвиденных проблем с трафиком. «Что до планирования непредвиденных проблем с трафиком, я думаю, что стоит планировать предвиденные проблемы», – парировал он. Шоуп прославился благодаря своей книге «Высокая цена бесплатной парковки», в которой он во многом внес ясность в процесс, который на самом деле имеет место, когда мы движемся из пункта А в пункт Б.

Бедного водителя стоит пожалеть! Идеальное парковочное место, в понимании Шоупа, – то, в котором умело соблюден точный баланс между стоимостью места парковки, неудобством от ходьбы пешком, временем, затраченным на поиски свободного пространства (сильно различается в зависимости от района, времени суток и т. д.), и сожженным за все это время бензином. Условия уравнения меняются с количеством пассажиров в автомобиле, которые могут разделить между собой плату за парковку, но не временем, потраченным на поиски места или на то, чтобы дойти пешком от места парковки до нужного пункта. Водитель должен учитывать, что пространство с наибольшим количеством свободных парковочных мест будет пользоваться наибольшим спросом. Поиски парковки всегда включают в себя элемент теории игр: пока вы пытаетесь перехитрить всех водителей на дороге, они, в свою очередь, пытаются перехитрить вас[5]. Таким образом, большинство проблем с парковкой сводится к одному фактору – уровню заполненности. Это отношение общего числа парковочных мест к количеству занятых в данный момент. Если уровень заполненности низкий, то можно без проблем найти хорошее место. Если же он высок, то поиск хоть какого-нибудь места, где можно было бы оставить машину, становится поистине сложной задачей.

Шоуп утверждает, что проблемы с парковкой возникли вследствие политики городских властей, которая привела к невероятно высокому уровню заполненности. Если плата за парковку в определенных районах слишком низкая (или – о ужас! – парковка и вовсе бесплатная), то большинство автолюбителей будет стремиться припарковаться именно там, а не чуть подальше, откуда придется немного пройти пешком. Таким образом, каждый старается встать там, но все места оказываются заняты, и люди в конечном счете тратят уйму времени и бензина, кружа по району в поисках парковочного места.

Решение Шоупа предполагает установку цифровых паркоматов, способных корректировать стоимость парковки по мере возрастания спроса (такой проект сегодня реализуется в центре Сан-Франциско). Цены устанавливаются исходя из уровня заполненности, и, по версии Шоупа, этот показатель должен быть в районе 85 % – довольно большой отрыв от 100 % забитых тротуаров большинства крупных городов. Он отмечает, что заполненность, возрастающая с 90 до 95 %, означает всего лишь на 5 % больше машин, зато удваивает количество времени, затрачиваемого водителем каждой из них на поиски места.

Ключевой момент влияния уровня заполненности на стратегию парковки становится очевиден, стоит нам только признать, что процесс парковки – это и есть проблема оптимальной остановки в чистом виде! Каждый раз, когда вы, проезжая по улице, видите свободное парковочное место, вам нужно принять решение: припарковаться здесь или проехать чуть ближе к конечному пункту и попытать удачи там?

Представьте, что вы едете по бесконечно длинной дороге, парковочные места на которой расположены через равные промежутки, и ваша цель состоит в том, чтобы свести к минимуму расстояние, которое вам придется пройти пешком от машины до конечного пункта. В этом случае решением станет правило «семь раз отмерь, один раз отрежь». Водитель, желающий найти оптимальный вариант парковки, должен проехать мимо всех свободных мест, находящихся дальше определенного расстояния от пункта назначения, а затем остановить свой выбор на первом же месте, которое встретится ему после этой точки отсчета. А вот расстояние, на котором «отмерь» превращается в «отрежь», зависит уже от соотношения мест, которые, вероятно, окажутся заняты, с общим их количеством – тот самый уровень заполненности. В таблице ниже приводятся расстояния для нескольких типичных соотношений.

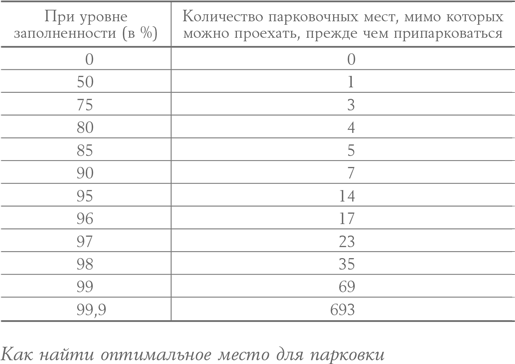
Если эта абстрактная бесконечная улица большого города имеет 99 %-ный уровень заполненности и всего 1 % свободных мест, то вам следует занять первое пустое место, которое попадется вам примерно за четверть мили до конечного пункта назначения (около 70 мест). Но если верить теории Шоупа, когда уровень занятости снизится до 85 %, вы можете не беспокоиться насчет парковки, пока вам не останется полквартала до места.

Но большинство из нас не катается по бесконечным прямым дорогам. Поэтому, как и в случае прочих проблем оптимальной остановки, исследователи рассмотрели ряд уловок. Например, они изучили стратегию оптимальной парковки в тех случаях, когда водитель может разворачиваться, когда чем ближе человек к месту назначения, тем меньше парковочных мест, и когда водитель составляет конкуренцию другим водителям, направляющимся в ту же точку. Но, каковы бы ни были условия задачи, наличие большего количества парковочных мест существенно облегчает жизнь. Это напоминание муниципальным властям: процесс парковки не так прост, как наличие ресурсов (мест) и обеспечение их максимального использования (занятость). Парковка – это процесс, который требует внимания, времени и затрат топлива и приводит к загрязнению окружающей среды и образованию заторов. Правильная политика решает эти проблемы. И, как ни парадоксально, наличие свободных мест в густонаселенных кварталах – признак того, что система функционирует правильно.

Мы поинтересовались у Шоупа, помогают ли ему его исследования в оптимизации его же собственных поездок на работу в Калифорнийский университет через все пробки Лос-Анджелеса. Вероятно, у лучшего в мире эксперта по парковке есть свои секретные приемы? «Все просто: я езжу на велосипеде», – ответил он.

Когда увольняться

В 1997 году журнал Forbes назвал Бориса Березовского самым богатым человеком в России; его состояние оценивалось примерно в $3 млрд. Всего десятью годами раньше он жил на зарплату сотрудника Академии наук СССР. Свои миллиарды он заработал на промышленных связях, появившихся у него в ходе исследований с целью основания компании-посредника между иностранными автоконцернами и советской автомобилестроительной компанией «АвтоВАЗ». Впоследствии компания Березовского стала крупным дилером машин «АвтоВАЗа» благодаря использованию схемы оплат в рассрочку, что в условиях гиперинфляции рубля имело огромное преимущество. На заработанные средства Березовский приобрел право на частичное владение «АвтоВАЗом», а затем вошел в совет директоров телеканала ОРТ и, наконец, компании «Сибнефть». Будучи представителем нового класса олигархов, он активно участвовал в политике, поддерживая перевыборы Бориса Ельцина в 1996 году и кандидатуру Владимира Путина в качестве его преемника в 1999 году.

Но в дальнейшем удача отвернулась от Березовского. Вскоре после избрания Путина на должность президента Березовский публично выступил против предложенных конституционных реформ, расширяющих президентские полномочия. Дальнейшие его публичные критические высказывания в адрес Путина привели к серьезному ухудшению их отношений. В октябре 2000 года, когда Путину был задан вопрос относительно критических замечаний Березовского, он ответил следующее: «Государство держит в своих руках дубину, которую применяют только один раз, но по голове. Пока государство эту дубину не использовало ‹…›. Когда мы серьезно рассердимся, мы, не колеблясь, применим ее…» Месяцем позже Березовский навсегда покинул Россию и эмигрировал в Англию, где продолжил критиковать режим Путина.

Вопрос, как вовремя уйти, когда ты на коне, анализировался в различных его проявлениях, но наиболее иллюстративным в ситуации с Березовским будет – да простят нас российские олигархи! – «задача грабителя». В этой задаче преступник может беспрепятственно совершить некоторое количество грабежей. Каждый из них сулит грабителю определенную выгоду, и каждый раз у него есть шанс эту выгоду получить. Но, если грабителя поймают и арестуют, он потеряет всю накопленную добычу. Каким алгоритмом ему стоит воспользоваться для максимизации своего ожидаемого дохода?

Тот факт, что данная проблема имеет решение, мало обрадует режиссеров фильмов об ограблениях: когда бандиты являются к старому гангстеру, отошедшему от работы, и уговаривают его в последний раз пойти на дело, хитрому вору остается только прикинуть числа. Тем более что результаты довольно наглядны: количество грабежей, которые вы хотите совершить, примерно равно шансам выйти сухим из воды, разделенным на вероятность быть пойманным. Если вы опытный вор и ваши шансы успешно провернуть дело равны 90 % (и 10 %, соответственно, вероятность его провалить), то стоит оставить свое ремесло после 90/10 = 9 грабежей. А неуклюжий новичок, чьи шансы на удачу 50/50? В первый раз вы ничего не потеряете, но не стоит искушать судьбу повторно.

Невзирая на опыт Березовского в решении задач оптимальной остановки, его история заканчивается весьма печально. Березовский умер в марте 2013 года; его тело было обнаружено телохранителем в запертой изнутри ванной комнате его дома в Беркшире. В официальном заключении патологоанатомического исследования сказано, что он покончил с собой – повесился, потеряв бóльшую часть своих богатств в результате ряда громких судебных процессов с участием своих врагов в России. Возможно, ему следовало остановиться раньше – накопив, к примеру, всего несколько десятков миллионов долларов и не влезая в большую политику. Но, увы, это было не в его правилах. Один из друзей Березовского, математик Леонид Богуславский, рассказал историю из времен их общей далекой юности о том, как они отправились на одно из подмосковных озер покататься на водных лыжах и у них сломался катер. Вот как Дэвид Хоффман описывает этот случай в своей книге «Олигархи»:

Как ни странно, это стремление никогда не сдаваться – во что бы то ни стало! – описывается и в материалах по проблеме оптимальной остановки. Возможно, это не выглядело очевидным в том широком спектре проблем, который мы рассматривали, но существуют последовательные задачи принятия решений, для которых правило оптимальной остановки не работает. Простой пример – игра «Утроить или потерять». Представьте, что у вас есть $1 и вы можете играть в эту игру бессчетное количество раз: поставьте на кон все деньги и получите 50 %-ный шанс утроить сумму и такой же 50 %-ный шанс все потерять. Сколько раз вам нужно сыграть? Несмотря на кажущуюся простоту, к этой задаче неприменимо правило оптимальной остановки, так как с каждой новой игрой ваш средний прирост становится чуточку выше. Начав с $1, вы в половине случаев получите $3, а в половине случаев – $0, так что в среднем вы ожидаете завершить первый раунд с $1,5 в кармане. Тогда, если в первом раунде вам повезло, появляется возможность во втором туре остаться либо с $9, либо с $0 – и средний выигрыш составляет уже $4,5. Математика утверждает, что вы всегда будете продолжать играть. Но если следовать этой стратегии, то в конечном итоге вы потеряете все. Некоторых проблем лучше избегать, нежели решать их.

Всегда останавливайтесь

Мы рассмотрели примеры конкретных людей, столкнувшихся в жизни с необходимостью решить проблему оптимальной остановки. Очевидно, что большинство из нас ежедневно встречается с этой проблемой в той или иной форме. Касается ли это секретарей, женихов (невест) или жилья, жизнь полна проблем оптимальной остановки. И главный вопрос заключается в том, действительно ли мы следуем наилучшей стратегии – благодаря эволюции, или образованию, или интуиции?

На первый взгляд, ответ – нет. Около дюжины исследований привели к такому результату: большинство людей, как правило, останавливаются слишком рано, оставляя лучшие варианты нерассмотренными. Чтобы глубже разобраться в данной ситуации, мы побеседовали с Амноном Рапопортом, профессором Калифорнийского университета в Риверсайде, который более 40 лет проводил эксперименты по оптимальной остановке.

Исследование, наиболее близкое к классической проблеме секретаря, было проведено Рапопортом и его соратником Дэррилом Сиэлом в 1990-х. В рамках этого исследования люди прошли через многократно повторяющиеся варианты проблемы секретаря, имея каждый раз от 40 до 80 претендентов на должность. Средний процент отсмотренных кандидатов, на котором поиски лучшего прекращались, составил 31 % – что довольно близко к оптимальным 37 %. Большинство руководствовались правилом «семь раз отмерь, один раз отрежь», но «отрезали» раньше, чем следовало, в четырех случаях из пяти.

Рапопорт признался, что он всегда помнит об этом, когда сталкивается с проблемами оптимальной остановки в повседневной жизни. В поисках квартиры, к примеру, он всегда борется с желанием поскорее заключить сделку. «Хотя по природе своей я очень нетерпелив и готов снять первую же квартиру, я стараюсь держать себя в руках!»

Но это нетерпение подводит нас к еще одному нюансу, который мы ранее не принимали во внимание в проблеме секретаря: роль времени. В конце концов, весь период, что вы ищете секретаря, у вас по факту нет секретаря! Более того, вы тратите дни на проведение собеседований вместо того, чтобы заниматься своей работой.

Этот вид расходов вполне объясняет, почему в процессе решения проблемы секретаря люди останавливаются в поисках раньше положенного срока. Сиэл и Рапопорт продемонстрировали, что если стоимость собеседования с каждым из кандидатов составит, предположим, 1 % от стоимости поиска лучшего секретаря, то оптимальная стратегия как раз совпадет с той, где люди перешли от слов к делу во время эксперимента.

Загадка в том, что в исследовании Сиэла и Рапопорта стоимость поисков не учитывалась! Так почему же все люди в лаборатории действовали как один?