Валерий Альмухаметов Вычислительная математика
Методы вычислительной математики делятся на точные и приближенные. Точные методы применяются в тех случаях, когда известны расчетные формулы, а также конкретное значение коэффициентов в них.
Существуют ситуации, когда расчетная формула неизвестна, или слишком сложна; величины, которые используются в вычислениях, заданы неявно; коэффициенты, содержащиеся в уравнениях, известны лишь приблизительно. Поэтому важное значение приобретают способы приближенного нахождения решения и оценки степени их точности.
Предлагаются к изучению простейшие численные модели, решение систем линейных уравнений, численное интегрирование и дифференцирование, методы решения задачи Коши для обыкновенных дифференциальных уравнений, методы конечных разностей решения уравнений в частных производных.
Методы вычислительной математики применяются также для поиска экстремального значения целевой функции в оптимизационных задачах, в том числе в нелинейных.
При обработке результатов эксперимента часто возникает задача построения эмпирической формулы, дающей аналитическое выражение функциональной зависимости, заданной таблицей. Для этого пользуются аппроксимацией функций по способу наименьших квадратов.
При использовании численных методов необходимо помнить о физической сущности рассматриваемых математических задач.
Некоторые задачи вычислительной математики можно решить, используя возможности табличного процессора Excel. Практически все задачи вычислительной математики можно решить в среде программного продукта Mathcad.
©Альмухаметов В.
НАХОЖДЕНИЕ ПОЛИНОМА ПО СХЕМЕ ГОРНЕРА
Для вычисления полинома n-й степени можно использовать схему Горнера: Y=((…((an*x +an-1)*x + an-2)*x +… +a2)*x + a1)*x + a0
рекуррентная формула при этом выражается в виде:
i = n Yi = аn Yi – 1= Yi x + ai
Алгоритм метода

Пример программы на языке Pascal
VAR N,I:INTEGER;X,Y:REAL;A:ARRAY[0..10] OF REAL;
BEGIN
WRITE('Введите N=');READLN(N);
WRITE('Введите X=');READLN(X);
WRITELN('Введите коэффициенты:');
FOR I:=0 TO N DO BEGIN
WRITE('A[',I,']=');READLN(A[I]);END;
Y:=A[N];
FOR I:=N-1 DOWNTO 0 DO Y:=Y*X+A[I];
WRITELN('Результат Y=',Y); END.
ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Задача численного интегрирования состоит в нахождении приближенного значения интеграла. Отрезок (ab) разбивается на определенное число интервалов N, в зависимости от требуемой точности вычисления.
Формула ПРЯМОУГОЛЬНИКА 
шаг: h=(b-a)/N
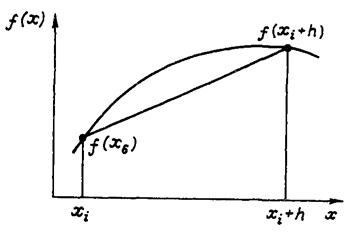
Геометрическая интерпретация метода:

Формула ТРАПЕЦИИ


шаг: h=(b-a)/N О – показатель точности вычислений
Геометрическая интерпретация метода:
Алгоритм метода трапеций:

Решить задачу:
Методом трапеций найти значение интеграла функции Y = x – Cos(x) в пределах от 0 до 2.
Пример программы (Pascal):
PROGRAM P10;
FUNCTION FUN(X:REAL):REAL;
BEGIN
FUN:=X-COS(X); END;
VAR H,X,Y,A,B:REAL; I,N:INTEGER;
BEGIN
WRITELN('Ввести данные A(0),B(2),N(1000) = ');
READ(A,B,N);
X:=0; Y:=0; H:=(B-A)/N;
FOR I:=1 TO N-1 DO BEGIN
X:=X+H;Y:=Y+FUN(X);END;
Y:=H/2*(FUN(A)+FUN(B)+2*Y);WRITELN('Результат= ',Y);
END.
(Результат для 1000 шагов: 1.09070287627348)
Решить задачу:
Задача. Найдите значение определенного интеграла от функции  на интервале [1; 4], количество разбиений n = 52.
на интервале [1; 4], количество разбиений n = 52.
Пример программы на языке Pascal
CONST N = 52; A = 1; B = 4;
VAR Y0, YN, X, S, H: REAL;I: INTEGER;
BEGIN
H := (B-A)/N; Y0 := SQR(LN(A))/A;
YN := SQR(LN(B))/B; S := (Y0 + YN)/2;
FOR I:= 1 TO N-1 DO
BEGIN
X := A + I*H;
S := S + SQR(LN(X))/X
END; S := S*H;
WRITELN (‘ИНТЕГРАЛ РАВЕН ’, S);
END.
Подпрограмма на языке Basic
10 DEF FNA(X)=EXP(-Х*Х)
20 PRINT "N,B0,B9,H1"; : INPUT N,B0,B9,H1
30 C=2/SQR(PI) : A=0 : S1=0
40 FOR B=B0 TO B9 SТЕР H1
50 GOSUB 100
60 S1=S1+S : A=B
70 PRINT B,C*S1 : NEXT В
90 GOTO 10
100 H=(B-A)/N : S1=(FNA(A)+FNA(B))/2
110 FOR I = 1 TO N-1 : S=S+FNA(A+ I *H) : NEXT I
120 S=S*H
190 RETURN
110 REM МЕТОД ТРАПЕЦИИ
120 INPUT . “Входные переменные A,B,N =”;A,B,N
130 H = (B-A)/N
140 S = O
150 X = A
160 FOR I = 1 TO N-1
170 X = X+H
180 S = S + FNY (X)
190 NEXT I
200 S = H*(FNY(A) + FNY(B) + 2*S) / 2
210 RETURN
Подпрограмма на языке Pascal
VAR N,I,K:INTEGER; A,B,B0,B9,H,C,S,S1:REAL;
FUNCTION F(X:REAL):REAL;BEGIN
F:=EXP(-X*X);END;
PROCEDURE TRAP(VAR A,B:REAL;
N:INTEGER; FUNCTION F:REAL;S:REAL);
VAR I:INTEGER;H:REAL;
BEGIN H:=(B-A)/N;S:=(F(A)+F(B))/2;
FOR I:=1 TO N-1 DO S:=S+F(A+I*H);
S:=S*H;END;
BEGIN C:=2/SQRT(3.14159265);
REPEAT WRITE('N,B0,B9,H?'); READLN(N,B0,B9,H);
K:=ROUND((B9-B0)/H+1.0); B:=B0; A:=0.0; S1:=0.0;
FOR I:= 1 TO K DO BEGIN TRAP(A,B,N,F,S); S1:=S1+S; A:=1.;
WRITELN(B,' ',C*S1); B:=B*H; END; UNTIL FALSE;END.
Формула СИМПСОНА

S= (b-a)/(6N)(f (x0) + f (x2N) + ∑i=12N-1 (3 + (-1) i-1) f (xi)) шаг:h=(b-a)/2N
Геометрическая интерпретация метода:

Пример программы на языке C#
Программа реализует оба метода – ТРАПЕЦИЙ и СИМПСОНА для функции f(x) с подбором шага интегрирования.
public double f(double x) {return x-Math.Cos(x);}
while (Math.Abs(r – r1) > p) { r1 = r; s=0; x=0;
if (radioButton1.Checked == true) k = n; else k = 2 * n;
h = (b – a) / k; for (int i=1;i<=k-1;i++) { x=x+h;
if (radioButton1.Checked == true) s = s + f(x);
else s = s+(3+Math.Pow(-1,i-1))*f(x); }
if (radioButton1.Checked == true) { r = h * (f(a) + f(b) + 2 * s) / 2; }
else { r = h * (f(a) + f(b) + s) / 3; }
n = n + 10; } textBox1.Text=Convert.ToString(r);
textBox2.Text=Convert.ToString(n);
Пример программы на языке Pascal
VAR I,K:INTEGER; Е,Z,Z0,Z9,H,S:REAL;
FUNCTION F(X:REAL):REAL;
BEGIN F:=SQRT(1.0-Z*SQR(SIN(X)); END;
PROCEDURE SIMPE(A,B,E:REAL; FUNCTION F:REAL;VAR S:REAL);
VAR I:INTEGER; C1,H,H2,S1,S2,S3,X:REAL;
BEGIN E1:=E*15.0; H:=(B-A)/2;
S:=2*F(A+H); S1:=F(A)+F(B)+S; S:=S1+S;
REPEAT S2:=0.0; S3:=S; H2:=H; H:=H/2; X:=A+H;
WHILE (X
BEGIN
REPEAT WRITE ('C,Z0,Z9,H?');READLN(C,Z0,Z9,H); K:=ROUND((Z9-Z0)/Н+1.0); Z:=Z0;
FOR I:=1 TO К DO BEGIN SIMPE(0.0,3.1415925/2,E,F,S);
WRITELN(Z,' ',S); Z:=Z+H; END; UNTIL FALSE; END.
Пример программы на языке Basic
10 DEF FNA(Х) =SQR(1-Z*SIN(X)^2)
20 PRINT "E,Z0,Z9,H1";: INPUT E,Z0,Z9,H1
30 A=0 : B=PI/2
40 FOR Z=Z0 ТО Z9 STEP H1
50 GOSUB 100
40 PRINT Z,S : NEXT Z
90 GOTO 10
100 E1=E*15 : H=(B-A)/2
110 S=2*FNA(A+H) : S1=FNA(A)+FNA(B)+S : S=S1+S
120 S2=0 : S3=S : H2=H : H=H/2
130 FOR X=A+H TO В STEP H2 : S2=S2+FNA(X):NEXT X
140 S2=2*S2 : S1=S1+S2 : S=S1+S2
150 IF ABS(1-S/(2*S3))>E1 THEN 120
140 S=S*H/3
190 RETURN
Метод МОНТЕ-КАРЛО
Программно генерируются случайные числа и значение интеграла определяется как соотношение количества чисел, попавших в пределы функции, к общему количеству чисел.
Геометрическая интерпретация метода:

Пример программы на языке Basic
10 DEF FNY(X)=COS(P*X-Z*SIN(X))
20 PRINT "ВАРИАНТ"; : INPUT I
30 PRINT "N,P,Z"; : INPUT N,P,Z
35 A=0 : B=PI
40 IF I = 1 THEN GOSUB 100
50 IF I=2 THEN GOSUB 200
60 PRINT "S="S/PI
90 GO TO 20
100 H=B-A : S=0
110 FOR I = 1 TO N : S=S+FNY(A+RND(1)*H) : NEXT I
120 S=H*S/N
190 RETURN
200 H=B-A : S=0 : R=0
210 F=FNY(A+RND(1)*H)
215 IF RND(1) 220 R=R+1 : IF R< N THEN 210 230 S=H*S/N 290 RETURN РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ ВИДА – ФУНКЦИЯ ОТ Х = 0 Метод половинного деления Уравнение может быть записано в общем виде: F(X)=0. Решение задачи состоит из двух этапов: 1) отделение корней – выделение отрезков [ab], принадлежащих области определения функции f(x), на которых расположен один и только один корень уравнения, то есть один нуль функции f(X). 2) уточнение корней с любой степенью точности – построение процесса, позволяющего как угодно сузить границы выделенного отрезка. Критерием является следующий: функция f(x) на отрезке [a b] должна быть непрерывна и монотонна, а ее значения на концах отрезка должны иметь разные знаки. Для отделения корней используются два метода. Аналитический метод: Для отделения действительных корней необходимо указать интервалы монотонности функции f(x), т.е. интервалы, в которых знак первой производной постоянный, а для этого решить уравнение f′(x) = 0 и подсчитать значение функции f(x) в точках корней уравнения и в граничных точках области определения функции. Отрезки, на концах которых у функции разные знаки, содержат корень. Графический метод: Нужно построить график функции f(x) и выделить отрезки, где функция непрерывна, монотонна и имеет разные знаки на его концах. Алгоритм метода половинного деления: Геометрическая интерпретация метода: Решить задачу: Методом половинного деления найти корень уравнения x-Cos(x)=0. Пример программы на языке C# double x, left = 0, right = 1; do { x = ( left + right ) / 2; if ( ( Math.Cos(x) – x ) * ( Math.Cos(left) – left ) < 0 ) right = x; else left = x; } while ( Math.Abs( right – left ) >1e-4 ); Console.WriteLine( "Корень равен " + x ); Пример программы на языке Pascal PROGRAM P9; FUNCTION FUN(A:REAL):REAL; BEGIN FUN:=A-COS(A); END; VAR A,B,X:REAL; BEGIN WRITELN('Ввести интервал А и В для поиска корня = '); READLN(A,B); REPEAT X:=0.5*(A+B); IF FUN(X)*FUN(A)<0 THEN B:=X ELSE A:=X; UNTIL ABS(A-B)<1E-4; WRITELN(' Корень уравнения ',X); END. (Тест: Интервал 0 и 1; Ответ = 0.73907470703125) Решить задачу: Найти корень уравнения на отрезке [1; 2] с точностью =10-4 методом половинного деления. Пример программы на языке Pascal CONST A = 1;B = 2;EPS = 1E-4; VAR X1, X2, X, Y1, Y2: REAL;F : BOOLEAN; BEGIN X1 := A; X2 := B; F := TRUE; WHILE F DO IF ABS (X1 – X2) > EPS THEN BEGIN Y1 := COS(2/X1) – 2*SIN(1/X1) + 1/X1; X := (X1 + X2)/2; Y2 := COS(2/X) – 2*SIN(1/X) + 1/X; IF ABS(Y2) > EPS THEN IF Y1*Y2 > 0 THEN X1:= X ELSE X2:= X ELSE F := FALSE END ELSE F:= FALSE; WRITELN (‘КОРЕНЬ УРАВНЕНИЯ ’,X); END. Ответ 1,875 Пример программы на языке Basic 10 DIM P(9) 20 PRINT " А,В,Е " ; : INPUT А,B,Е 30 PRINT "СКОЛЬКО ПАРАМЕТРОВ"; : INPUT N 40 FOR К=1 TO N : PRINT "Р"К; : INPUT Р(К) : NEXT К 50 GOSUB 100 60 PRINT "Х=”Х 90 GOТО 20 100 Х=А : GOSUB 200 110 S=SGN(F) 120 X = (А+В)/2 : GOSUB 200 130 IF ABS(F)<Р(2) THEN RETURN 140 IF SGN(F)=S THEN A=X : GOTO 160 150 B=X 160 IF B-A>E THEN 120 190 RETURN 200 R=1 : R1=SQR(1-Х) 210 R2=(R+R1) /2 : R1=SQR (R*R1) : R=R2 220 IF R-R1 >P(2) THEN 210 230 F=R*P(1)-PI/2 290 RETURN Пример программы на языке Pascal VAR P: ARRAY [1..9] OF REAL; A,B,X,E:REAL;N,K:INTEGER; FUNCTION F(X:REAL):REAL; VAR R,R1,R2: REAL; BEGIN R:=1.0; R1:=SQRT (1.0-X); WHILE R-R1 >P[2] DO BEGIN R2:=(R+R1)/2; R1:=SQRT(R*R1); R:=R2; END; F:=(R+R1)*P[1]-3.14159265; END; FUNCTION SGN(X:REAL):INTEGER; BEGIN SGN:=0; IF X<0.0 THEN SGN:=-1; IF X>0.0 THEN SGN:=1; END; PROCEDURE DICH(VAR A,В,X,E,E1:REAL; FUNCTION F:REAL); VAR I:INTEGER; R:REAL; BEGIN I:=SGN(F(A)); WHILE B-A>E DO BEGIN X:= (A+B) /2; R:=F(X); IF ABS(R) IF SGN(R)=I THEN A:=X ELSE B:=X;END;END; BEGIN REPEAT WRITE(‘A,B,E?'); READLN(A,В,E); WRITE('СКОЛЬКО ПАРАМЕТРОВ? '); READLN(N); FOR K:=1 TO N DO BEGIN WRITE(‘P(‘,K:2, ')? '); READLN (Р[К]);END; DICH(A,B,X,E,P[2],F); WRITELN('X=’,X); UNTIL FALSE; END. Метод итераций Уравнение f(x)=0 представляется в виде x=φ(x),где φ(x)определяется одним из способов: φ(x)= x – αf(x),где α=const φ(x)= x + ρ(x)f(x), где ρ(x)-произвольная функция не имеющая корней на отрезке (a/b). Метод простой итерации определяется формулой: xn+1=φ(xn), n=0,1,2,3… где n-номер итерации,x0-произвольно заданное начальное приближение. Процесс сходится к корню уравнения, если на отрезке (ab) выполняется условие: φ′(x) <= q < 1.
